基于MIKE 21的汾河水库挟沙水流水质数值模拟研究

2022-03-08张月婷徐明德原文超

四川环境 2022年1期

张月婷，徐明德，原文超

(1.中国辐射防护研究院，太原 030006；2.太原理工大学，太原 030024)

前言

汾河水库是引黄入晋工程的调蓄水库，是山西省最大的饮用水水库[1]。上世纪初，国内外就已开展了泥沙规律的研究工作，但研究内容多局限于泥沙自身运动分析，例如泥沙的运输与淤积[2-3]，对于泥沙对水体水质的影响规律研究却很少涉及，而对于北方干旱地区水库的相关研究更是鲜有报道。本文选取汾河水库为研究对象，以汾河水库水动力[4]—泥沙转移—富营养化耦合模型[5]进行模拟分析，研究高含量SSC对汾河水库库区水质产生的影响，从而揭示SSC对库区水质的影响规律。

1 研究区域

1.1 区域概况

汾河水库位于汾河干流上游段，是太原地区主要水源地。南北长15 km，东西宽5 km，其总面积约达32 km2。汾河水库的流域总面积达到5 268 km2，平均流量每秒可达21.9m3，水库总流量为7.22 亿m3，泥沙总库容为3.45亿m3。

1.2 水质监测

1.2.1 监测点位：考虑汾河水库自然特点，设置A、B、C、D、E、F6个监测点，其中A点和B点分别位于汾河入库处和涧河入库处，C点、D点和E点分别位于库区上段、中段和后段，F点位于坝址处，各监测点的位置如图1所示。

图1 汾河水库监测点位Fig.1 Monitoring sites of Fenhe reservoir

1.2.2 监测对象：表层水样、沉积物样品。

1.2.3 监测因子及方法：包括SSC、Chla、TP、TN、固态氮等监测因子，监测方法选用《水质悬浮物的测定重量法》(GB/T 11901-1989)中的重量法、冷冻浸提法、分光光度法、紫外分光光度法[6]、超声萃取法[7]。

1.2.4 监测时间：2017年6月11日～2017年9月23日。

2 汾河水库模型的构建

2.1 水动力模型

本模型的理论基础为静水压力和布辛尼克斯(Boussinesq)[8]假设，纳维叶-斯托克斯(Navier-Stokes)[9]方程对水动力方程进行控制。二维水动力模型如下：

(1)

(2)

(3)

其中：φ(x,y,t)为表面高程；p、q为在x、y方向上的流量分密度；h(x,y,t)为水深均值；C为固定值，谢才系数；g为重力加速度；τs(V)为风应力；Vx、Vy分别为风应力沿x、y方向的分量；Ω(x,y)为科里奥利参数；Pa(x,y,t)为大气压；ρw为水密度；S为源质量；Six，Siy分别为在x、y方向上源质量的动量分量；τxx、τxy、τyy为在xx、xy、yy方向上的应力有效力。

2.2 泥沙转移模型

通过水深均一的二维模型(模型中非粘性泥沙颗粒的直径要求达到0.063 mm以上)来模拟泥沙转移。该模型通常用以分析湖泊水库中非粘性泥沙的絮凝，同时也可用以分析泥沙转移对水底高程的改变。模型如下：

(4)

其中：ρ为垂直方向上的泥沙平均质量密度；u、v为水流沿x、y方向上的流速；Dx、Dy为泥沙的扩散系数；Ti为源汇项。

2.3 富营养化模型

模型公式如下：

(5)

其中：C1为富营养化垂向平均浓度；Dx、Dy为x、y方向的扩散系数；kp为线性衰减率；CS为源浓度；S为点源排放量；Pc为富营养化过程组。

(6)

其中：ci为富营养化浓度；m为状态变量过程数。

3 汾河水库含沙水质模拟

3.1 水动力模拟

3.1.1 模拟范围

选取全库水域为模拟范围，运用GPS和Erdas工具对水库进行现场定位，同时依靠水库周边的地形特点，确定水库的边缘点坐标，通过地理信息处理技术将坐标进行数字化处理，确定汾河水库的水库边界。考虑水库周边环境存在一定复杂性，依据非结构化三角形网络系统将整个库区划分为3 160个三角网格，垂直方向无分层。水库模拟边界与地形见图1。

3.1.2 定解条件

3.1.2.1 初始条件：假定全部模拟区域均以静止状态开始，即u=v=0；水位初始值为沿水流方向取得的边界两端的平均值，即1 126.2 m。

3.1.2.2 边界条件：通过岸壁法处理闭边界，其处理方法为设置法线方向上的浓度和速度为零；汾河开边界，采用“干湿点判别法”的方式进行分析，增水时的水深不低于0.1 m，此时为“湿点”，按水域进行处理，退水时的水深为0.005 m，水速为零，视为 “干点”，按陆域来处理。

3.1.3 模拟参数率定和模型验证

3.1.3.1 模拟时间步长。模拟时间为2017年2月1日至2017年12月1日。依据线性方程，得到最终时间步长为3600 s，其满足CFL条件。

3.1.3.2 涡黏系数。用Smagorinsky[10]公式确定水平涡黏系数，其值为0.8。

3.1.3.3 摩擦力。通过曼宁公式确定摩擦力，曼宁系数值取32 m1/3/s。

3.1.3.4 降雨量与蒸发量。查阅汾河水库库区相关资料，获得在时间尺度上的降雨量和蒸发量。

3.1.3.5 源与汇。取进入汾河水库的水流为源汇项，北部汾河入水口和西部涧河入水口为汾河水库的主要进水口，汾河水库坝址处为出水口。每年7～8月，汾河水库处于枯水期，而在1、5、6、9～12月，汾河水库处于平水期，2～4月，汾河水库处于枯水期。丰水期，入库流量最大为60 m3/s，枯水期入库流量最小为4 m3/s。汾河水库的主要目的为下游提供灌溉用水和日常生活饮用水[11]。每年3月中旬至4月中旬、8月中旬至9月初，下游开闸放水灌溉，出口流量可达20～40 m3/s，其余时间则主要为古交矿区和太原市提供日常生活饮用水，此时水库的出水流量约为3.12 m3/s。依据不同时间段水量的变化，形成相应的时间序列。

3.1.3.6 参数率定和模型验证。以汾河水库的表面水位值为验证资料，经过模型参数调整，确定计算参数。模拟输出了2017年7月～2017年9月水库表面水位值时间序列，将输出水位值与2017年《山西水文月报》中的实际水位值进行对比，结果表明6月11日、6月20日、7月11日三天汾河水库的实际测量水位为：1 126.03、1 126.18、1 126.50 mm，通过模拟，所得到的水位为：1 126.00、1 126.15、1 126.48 mm。模拟表面水位值与水位实测值绝对误差小于0.03，相对误差小于0.003%，因此参数设置合理，模型可用性较高。

3.2 水动力—泥沙输移—富营养化模型

3.2.1 模拟范围

模拟范围为全库水域。

3.2.2 模型参数

3.2.2.1 模拟时间步长、涡黏系数、摩擦力、降雨量与蒸发量参数取值同水动力模拟一致。

3.2.2.2 源与汇。与水动力模拟所建立的时间序列一致之外，还需要对TN、TP以及Chla等进行检测并建立时间序列文件。例选取北部上游Chla浓度并建立时间序列，浓度介于0.021～0.048 mg/L。

3.2.3 耦合模型的参数率定与验证

3.2.3.1 水动力—泥沙耦合模型

选取2017年6月11日～2017年6月30日B点位置处的数据进行验证，通过实际数据的输入和调整，从而确定准确数据，数据类型主要包括：孔隙率系数为0.2，相对密度系数1.2，曼宁系数32 m1/3/s，扩散系数1，模型模拟输出结果与实际监测值对比结果如图2(a)所示。

3.2.3.2 水动力—富营养化耦合模型

选用2017年8月1日～2017年8月10日实地测量B监测点的Chla、TN、TP、DO等，通过模型对数值进行验证。因篇幅限制，本研究仅以Chla为例，在误差可接受范围内，对水质模型相关参数进行验证，结果见图2(b)。

以B点泥沙浓度为例，模拟值与实测值基本吻合。最大绝对值偏差7.5 g/m3，相对误差1.05%。因此本文构建的耦合模型具有可行性。

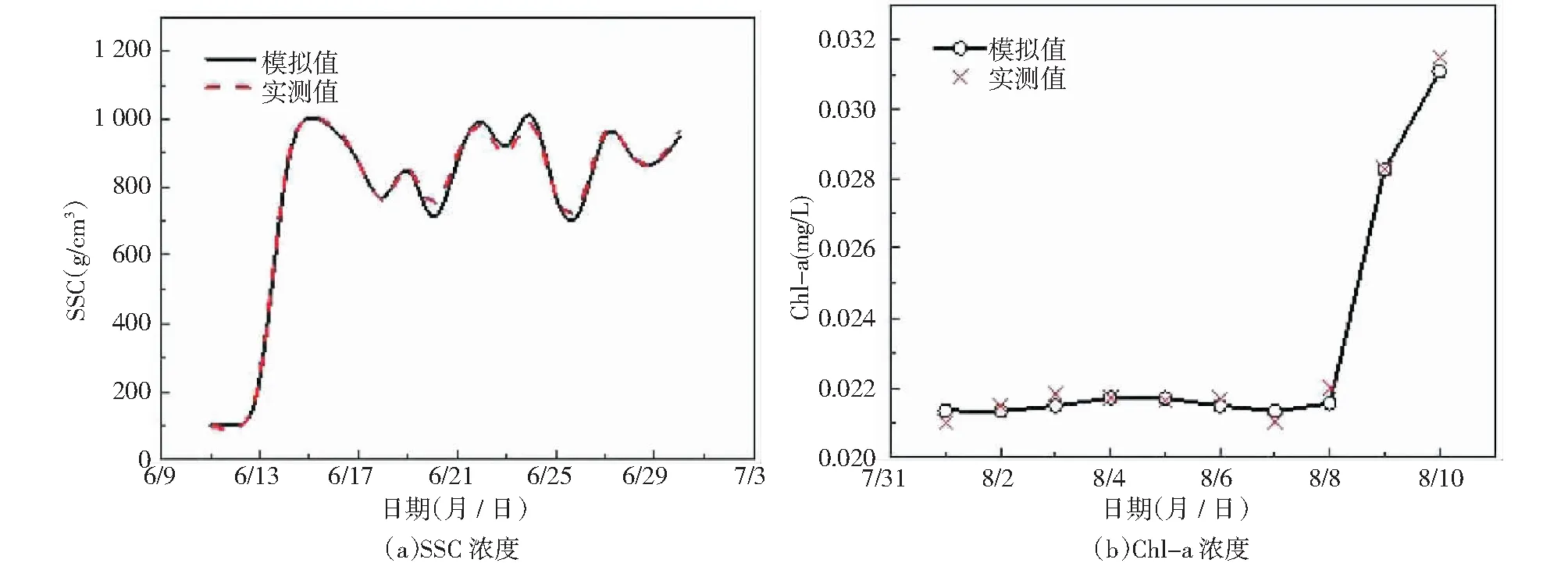
图2 B点模拟值与实测值对比Fig.2 Comparison of B the simalated value and measured value at point B

3.3 方案的设定

设置不同的模型方案，对各个方案进行对比分析，选出具有代表性的控制点分析汾河水库水质受到泥沙的影响。从空间距离上，依据库区入水口离坝址的远近顺序选取了6个代表性控制点，如图1所示。设定三种方案，方案1：水动力—泥沙耦合模型，为①；方案2：水动力—富营养化耦合模型，为②～④；方案3：水动力—泥沙—富营养化耦合模型，为⑤～⑦，方案设置分类见表1。其中，降水量、蒸散量、风力等，采用实际测量数据。模拟时间：2017年6月11日至2017年9月23日，共计104天。

3.4 模拟结果分析

3.4.1 模拟结果

在水动力模拟基础上，Chla、TP、TN、DO浓度模拟分布图，见图3。

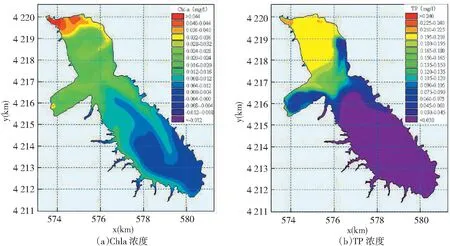
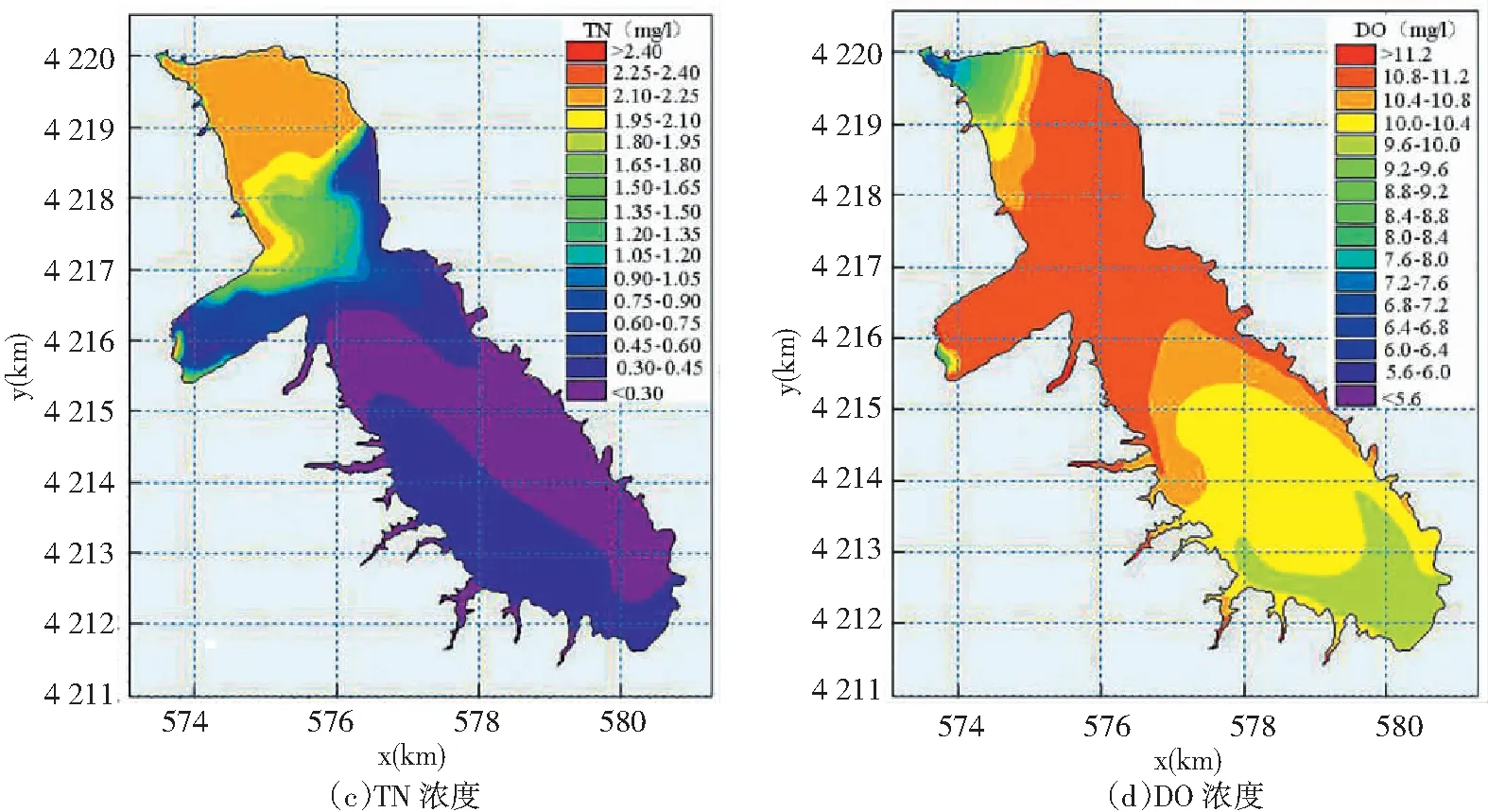
图3 Chla、TP、TN、DO浓度分布Fig.3 Distribution of Chla、TP、TN、DO concentration

3.4.2 结果分析

3.4.2.1 通过水动力—泥沙耦合模型模拟，分析泥沙浓度变化情况。以下为模拟结果：选择6个模拟点，以进水口位置为基准点，A、B较近，其次为C、D、E、F点，结合位置分为两组，具体仿真结果见图4。

图4 各监测点泥沙浓度变化图Fig.4 Sediment concentration variation of monitoring points

汛期SSC的时空分布：A点泥沙浓度的急剧增加主要来自汾河干流来水的直接补给；B点泥沙浓度的变化较为缓和。A、B两监测点的研究结果表明：2016年7月25日前后，两监测点的SSC浓度出现了剧烈增加，之后泥沙浓度达到峰值。实时监测结果显示，7月22日至7月28日，汾河干流的进水量为30～60 m3/s，涧河处，其进水量达到了本年最大值，为1.13～2.26 m3/s，这直接影响了SSC浓度，使其变化十分明显。A点与进水口距离较近，水体中泥沙的含量变化大，相反，C、D、E、F点与进水口距离远，泥沙的浓度变化可以忽略不计。综上所述：含沙水在某种程度上会对水库泥沙浓度产生影响，同时这种影响的范围也是有限的。

3.4.2.2 通过水动力—富营养化耦合模型和水动力—泥沙—富营养化耦合模型模拟，并选取具有代表性的监测点位，模拟不同时段下的Chla浓度、TP浓度、TN浓度、DO浓度，见图5。

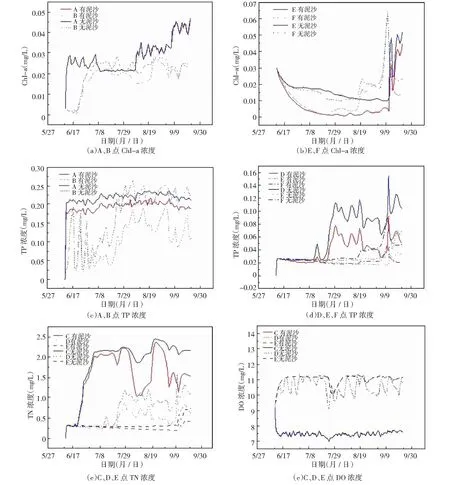
图5 各代表性监测点Chla、TP、TN、DO浓度变化图Fig.5 Variatiion of Chla、TP、TN、DO concentrations at representative monitoring points

(1)SSC对水库Chla的影响：汛期前期，Chla含量受到SSC的影响基本可以忽略不计；A、B点Chla含量在SSC大量存在前后差异不大，并趋于吻合。此外，在汛期前期，如果水库的水量进出发生变化的话，会对Chla的含量产生直接影响。汛期期间，B点高含量SSC存在时Chla含量比SSC不存在时越来越小。汛期过后，B点Chla浓度较非含沙水高。另外，由于E、F监测点距离进水口较远，这就导致水体中泥沙的含量对Chla的含量并无明显影响。综上，整体来说，在整个汾河水库体系中，水库进水对于Chla的含量影响并不是很大。

(2)SSC对水库TP的影响：SSC大量存在和SSC不存在两种情况下，各监测点位的TP含量总是前者高于后者。

(3)SSC对水库TN的影响：C点TN含量差异不大，D和E点TN的含量差距明显，当TN的浓度上升后，其浓度就很难下降，这种现象与TP的变化规律存在明显区别，当某些监测点受SSC的干扰作用较弱时，这种现象与水体中TP含量的时空分布规律是一致的，当进入水库的水不含SSC时，水体中TN的含量就会远大于进水存在大量泥沙的状况。

(4)SSC对水库DO 的影响：研究结果表明，SSC几乎对DO的含量不会产生影响，即使当水体中含有大量的SSC时，水体中的DO含量也几乎不会发生任何变化。因此泥沙存在与否，二者对DO含量的影响差异性不大。

3.5 底泥污染物释放量计算

根据经验公式进行底泥污染物释放量估算。

M=R×S×t×10-3

(6)

其中：M为底泥污染物释放量，t；R为污染物释放通量，mg/m2.d；S为库区面积，km2；t为释放时间，d，取t=104 d。

M’=C×S×h+C×Q×10-6

(7)

其中：M’为水体污染物总负荷，t；C为水体污染物平均浓度，mg/l；h为平均水深，m；Q为年出库水量。

由底泥污染物释放量计算得出，汛期后期，有2.5 t的污染物来自于底泥释放的TN，有4.16 t的污染物来自于底泥释放的TP，水库库区TN、TP的总负荷分别为615.33 t和16.47 t，此两者的贡献率分别为0.406%和25.25%，这一结果说明水库水体磷负荷以及富营养化是造成底泥内源磷释放的重要因素，需积极开展污染治理。

3.6 污染防治对策

(1)预防性措施：在汾河水库上游采取拦沙方式，减少泥沙入库，是控制悬浮泥沙入库的最根本方法。其中水土保持，防止流失，对减少水库淤积有着关键作用，同时还可以减少面源污染物，改善生态环境质量。(2)清淤措施：采用“蓄清排浑”的运行方式，在丰水丰沙年内，利用高含沙量的水流，在保持一定低水位的条件下，进行异重流排沙，通过及时打开排沙闸门的方式使泥沙高效排出，有利于改变下游水生生物的生长与繁殖。