基于CEEMDAN-LSTM模型的郑州市月降水量预测

罗上学，张美玲，聂雅梅，贾晓楠，曹瑞红，朱美婷，李晓娟

(甘肃农业大学理学院，甘肃 兰州 730070)

降水预测对农业生产和水资源利用具有重要意义。由于气象过程的多变性和随机性，要准确预测降水是非常困难的。近些年来，机器学习技术在复杂非线性过程建模中的应用效果很好[1- 2]。各种机器学习模型，如支持向量机、随机森林、BP神经网络和自适应神经模糊推理系统(ANFIS)，已被用于预测降水量并取得了不错的效果[3- 6]。虽然这些模型可以处理非线性数据，但它们很难识别降水量数据之间的长期依赖关系，其预测精度有待提高。长短期记忆(long short-term memory，LSTM)模型加入单元状态和门结构来控制信息的传递，可以有效学习时间序列中的长期依赖关系。由于LSTM对时间序列问题优秀的处理能力，被广泛应用于降水量预测建模。刘威等[7]使用遗传算法优化的LSTM模型对4个气象站的月降水量进行预测。刘新等[8]采用LSTM模型对青藏高原86个观测站的月降水量进行预测，结果表明LSTM模型整体预测精度高于传统模型。陈慧等[9]通过LSTM模型对川东地区逐月降水量进行预测，结果显示LSTM模型与随机森林模型相比具有普遍优势。然而，由于降水量呈现非线性，具有很强的复杂性，在某些月份会出现极端降水。但当LSTM模型单独用于高度非线性的降水量预测时，很难准确预测到降水量序列的突变，存在较大误差。

将数据去噪方法与数据驱动模型结合起来可以提高预测精度，经验模态分解(EMD)是最常用的数据去噪方法之一。EMD是一种优秀的非线性信号分析方法，它基于原信号局部极值点对信号进行分解[10]。由于EMD方法经常会遇到模态混叠问题，分解得到的本征模态函数(IMF)分量不能体现原序列的变化特征。集合经验模态分解(EEMD)通过往原始序列里添加高斯白噪声再求和平均，减轻了EMD的模态混叠程度，分解结果能更直观地体现原序列的变化特征[11]。目前，基于EEMD的混合模型已经成为水文和气象预报的常用工具。黄春艳等[12]采用EEMD-GRNN模型对郑州市年降水量进行预测，结果显示EEMD方法可以提高GRNN模型的性能。杨倩等[13]使用EEMD-LSTM预测天山北坡经济带的年降水量。但在实际应用中，EEMD方法添加白噪声的幅度没有确定的标准，经过集合平均后仍然会有一部分噪声残留下来，导致EEMD存在一定重构误差。完全集合经验模态分解(CEEMDAN)对添加的白噪声也一起分解，有效解决了EEMD分解速度慢和噪声难以完全抵消的问题[14]。张金萍[15]等使用CEEMDAN-ARMA模型预测年径流量，与单一ARIMA模型相比预测精度更高。本文建立了一种CEEMDAN-LSTM组合模型，对郑州市月降水量进行预测，并与LSTM、EEMD-LSTM和CEEMDAN-SVR模型的预测结果一起比较。

1 研究区域概况

郑州市是河南省省会，位于河南中部偏北。郑州市属于北温带大陆性季风气候，降水主要集中在夏季，其他季节的降水很少，因此郑州市容易受到旱涝灾害的影响。本文选用郑州站1951年1月—2020年12月的降水量数据进行研究，前90%数据用于模型训练，后10%数据用来验证模型预测效果，数据来自中国气象数据网(http://data.cma.cn)。郑州市降水量序列如图1所示，从中可以看出郑州市降水量具有很强的非平稳性和波动性。

2 研究方法

2.1 CEEMDAN方法

CEEMDAN方法在分解时加入自适应高斯白噪声，并且对噪声也进行分解，有效减小了重构误差。CEEMDAN需要添加噪声的次数比EEMD更少，提高了计算效率。CEEMDAN的具体分解步骤如下：

(1)在降水量P(t)中添加不同的高斯白噪声wi(t)：

Pi(t)=P(t)+ε0wi(t)，i=1，2，…，N

(1)

式中，ε0—当前分解阶段的信噪比。

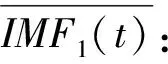
(2)

(3)计算第一个剩余分量r1(t)：

(3)

(4)然后用EMD算法对信号r1(t)+ε1E1(wi(t))分解，可得第二个模态分量：

(4)

其中Ej(·)是经过EMD分解后的第j个分量。

(5)对k=2，3，…，K，重复步骤(3)和(4)，可得：

(5)

(6)

(6)重复计算步骤(5)，直到剩余分量无法再分解(少于2个极值)，最后得到k个模态分量。分解的最终残差为：

(7)

最后降水量序列被分解为：

(8)

2.2 LSTM神经网络

当反向传播误差跨越多个时间步时，传统循环神经网络(RNN)容易发生梯度消失和爆炸问题，很难学习序列中的长期依赖关系[16]。LSTM神经网络引入了1个单元状态和3个门(输入门，遗忘门和输出门)来控制信息的流动，很好地解决了这个问题[17]。LSTM的结构如图2所示，其中单元状态可以储存过去的信息，3个门用来控制信息的传递和更新。LSTM的具体计算步骤如下：

图2 LSTM结构

(9)

it=σ(Wi·[ht-1，xt]+bi)

(10)

(11)

(12)

ot=σ(Wo·[ht-1，xt]+bo)

(13)

ht=ot*tanh(ct)

(14)

式中,xt—当前输入；ht-1、ht—t-1时刻和t时刻隐藏层的输出；Ct-1、Ct—t-1时刻和t时刻的单元状态；ft、it、ot—t时刻遗忘门、输入门和输出门的输出；Wf、Wi、Wc、Wo—权重向量;bf、bi、bc、bo—偏置向量。

2.3 CEEMDAN-LSTM模型

降水量数据具有很强的非线性和多变性，单一模型很难捕捉到降水量的变化规律。因此，本文采用CEEMDAN算法将降水量数据分解成一系列相对稳定的分量，再分别对每一个分量构建合适的LSTM模型，然后把所有分量的预测值求和得到降水量的预测值，具体步骤如图3所示。

2.4 模型评价指标

为了验证CEEMDAN-LSTM模型对降水量的预测结果，本文选取了3个经典的统计指标来评价，分别是均方根误差(RMSE)、平均绝对误差(MAE)、决定系数(R2)，具体的计算公式如下：

(15)

(16)

(17)

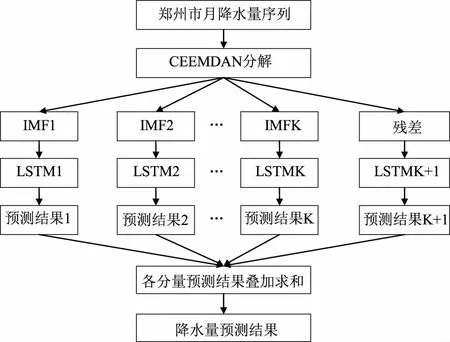
图3 CEEMDAN-LSTM流程图

3 结果和分析

3.1 降水量序列分解结果

对郑州市1951年1月—2020年12月的降水量序列进行CEEMDAN分解，得到8个模态分量和一个残差，如图4所示。8个模态分量频率依次递减，残差反映了降水量数据的总体变化趋势。与原始降水量数据相比，各分量波动更小，建模难度更低。

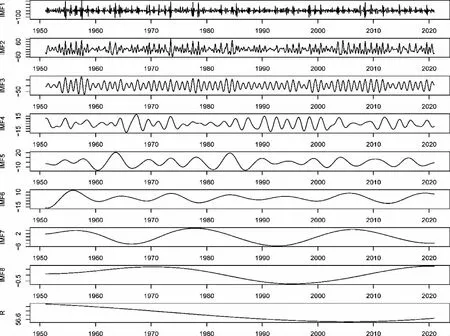
图4 郑州市降水量CEEMDAN分解结果

表1是郑州市月降水量序列及其分解结果的描述性统计。由表1可知，各分量的标准差比原始降水量序列的标准差小得多，说明各分量波动较小，离平均值更接近。此外，原始降水量序列的偏度和峰度都较大，说明原始降水量数据分布不对称并且存在较多极端值。相比之下，各分量的偏度接近0，峰度也更小，说明各分量的分布近似对称，极端值更少。因此，CEEMDAN是一种有效的数据分解方法，可以为LSTM模型提供更稳定的输入。

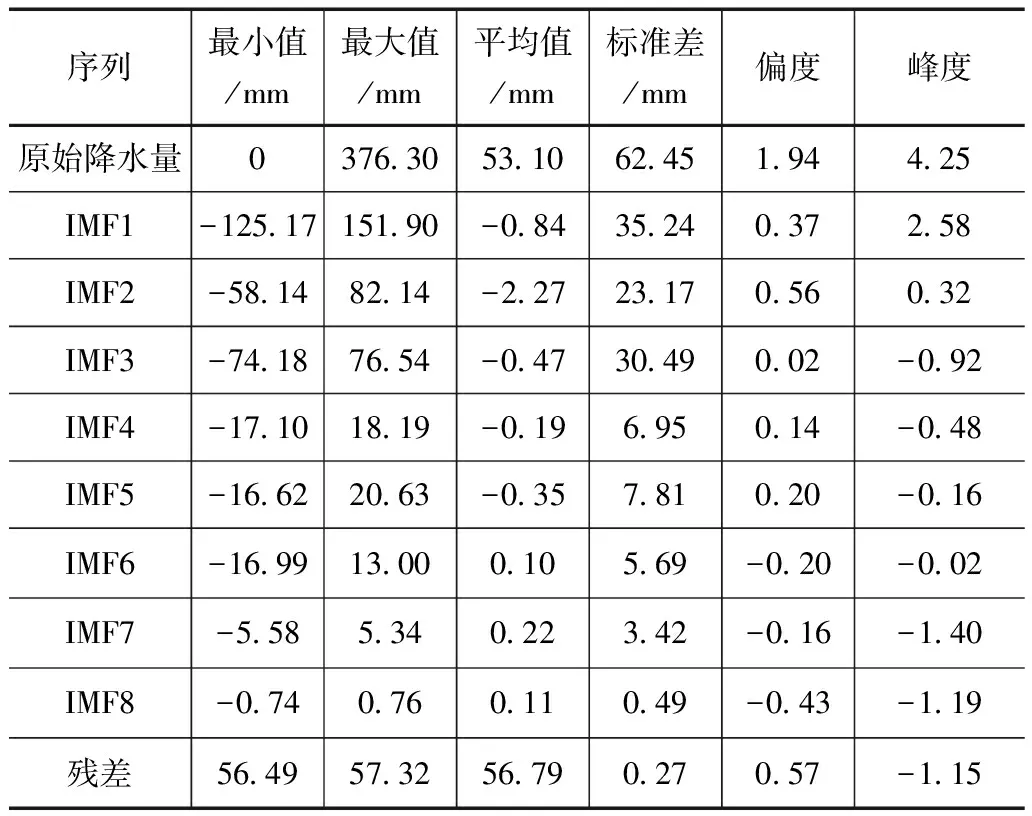
表1 原始降水量和分解结果统计

3.2 LSTM模型构建

对各模态分量和残差进行归一化处理，然后将前90%的数据用于训练LSTM模型，后10%的数据作为测试集来验证模型性能。采用一步预测方法对各分量预测，即用t时刻前l个数据(xt-l，xt-l+1，…，xt-1)作为模型输入来预测t时刻的数据xt，其中l是时间步长。LSTM网络在Keras平台上构建，使用的激活函数为tanh，优化器为Adam函数，损失函数为均方误差。经过分解之后的数据随机性大大降低，使用两层隐藏层只会增加模型的复杂度和计算时间，对提高精度没有明显作用，因此所有LSTM模型都只使用一层隐藏层。为避免模型过拟合，采用Dropout方法在训练时随机丢弃一些神经元。使用指数衰减法动态调整学习率，在训练初期设置较大的学习率来快速接近最优解，然后逐渐减小学习率，使模型更稳定，计算公式如下：

(18)

式中，μ—当前迭代次数；β—衰减速度，即经过β步迭代衰减一次，取值为200；λ—衰减系数，取值为0.95；η—初始学习率，取值为0.01；η′—更新后的学习率。

在训练过程中高频分量具有较高的复杂性，可以适当增加时间步长。在模型预测完之后需要将预测值逆归一化。由于各分量选取的时间步长不尽相同，每个分量的预测结果长度不一样，以最短的序列长度为准，将其他序列多出来的值舍弃。对所有分量的预测值求和得到郑州市月降水量的预测值。由于降水量没有负值，预测结果里的负值用0代替。

3.3 预测结果分析

为了验证混合CEEMDAN-LSTM模型的预测效果，选取了LSTM，EEMD-LSTM和CEEMDAN-SVR模型的预测结果进行对比，如图5所示。由图5可知，单一LSTM只能大致预测降水量的变化趋势，当某些月份降水量较多时LSTM的预测误差会迅速增大。与正常降水相比，极端降水事件更有可能对农业生产和人民生活造成危害，因此有必要提高对极端降水月份的预测精度。EEMD-LSTM和CEEMDAN-SVR模型的预测结果比LSTM好，在降水量较多的月份与实测值更接近，说明对降水量序列进行分解能提高模型的精度。CEEMDAN-LSTM模型的预测结果与实测值最接近，即使在降水量较多的月份也能准确预测，这是因为CEEMDAN将降水量序列里不同的波动特征完全分离出来，并且对加入的噪声也进行分解，减小了重构误差。经过CEEMDAN分解后的各分量与原始降水量相比更有规律，从而让LSTM模型能更好地捕捉到各分量的变化特征，有效提高了预测精度。

图6是不同模型的预测结果与降水量观测值对比的散点图，其中实线是对角线，虚线是模型预测值和降水量观测值的线性拟合。从图6中数据点的分布情况可以发现，LSTM模型的数据点比较分散，而且在降水量很多的月份LSTM模型的预测值远小于观测值，说明LSTM模型不能深入挖掘出随机性强的降水量序列的变化规律，其预测精度不够。EEMD-LSTM模型对极端降水的预测精度较高，但对正常降水的预测存在一定偏差。CEEMDAN-SVR模型对降水量的总体预测精度较高，但是对极端降水的预测值略小于真实降水量。CEEMDAN-LSTM模型的数据点几乎都分布在对角线上，说明CEEMDAN-LSTM模型对降水量的预测比较准确。从各模型预测值与降水量观测值的线性拟合可以看出，CEEMDAN-LSTM模型回归方程的系数和R2接近1，说明CEEMDAN-LSTM模型的结果与降水量观测值比较一致。

按照选取的统计指标对各模型的预测性能进行分析，结果见表2。由表2可知，单独使用LSTM模型对降水量的预测存在较大的误差。EEMD-LSTM、CEEMDAN-LSTM混合模型与LSTM模型相比，RMSE分别减少了36.44%和63.72%，MAE分别减少了23.29%和60.09%，R2分别提高了0.306和0.446，说明经过分解之后再建模预测可以有效提高模型预测精度，并且CEEMDAN对模型精度提升更大。CEEMDAN-LSTM模型预测精度高于CEEMDAN-SVR模型，这是由于LSTM能够很好地学习序列里的长期依赖关系，对时序数据的预测能力更强。在所有模型中，CEEMDAN-LSTM模型具有最小的RMSE、MSE和最高的R2，说明本文所使用的CEEMDAN-LSTM模型在降水量预测中具有一定优越性。

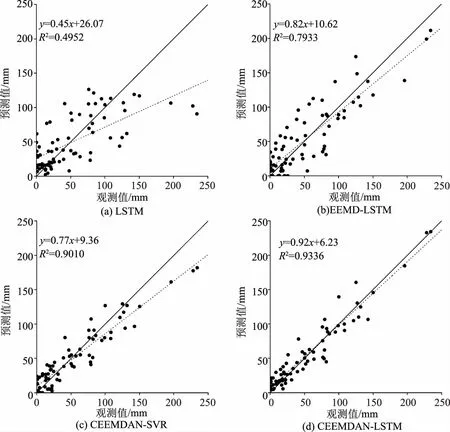
图6 降水量观测值和预测值的散点图

4 结论

本文将CEEMDAN和LSTM的优势结合起来，构建CEEMDAN-LSTM混合模型对郑州市月降水量序列进行预测。将降水量数据分解为一组更稳定的分量之后，模型更容易识别各分量的变化特征，预测精度得到了明显提升。CEEMDAN-LSTM模型的预测结果与真实降水量最接近，即使在降水量特别多的月份也有不错的表现。在选用的3个评价指标下，CEEMDAN-LSTM模型都表现出了最佳的性能，这表明本文提出的CEEMDAN-LSTM模型是预测郑州市月降水量的合适工具。

在未来的研究中，可以尝试将温度，气压，相对湿度和风速等气象变量输入模型来进一步提高预测精度。