冰蓄冷系统冷冻水供水温度设定方法研究

陈霈 牛洪海 管晓晨 杨玉

南京南瑞继保电气有限公司

0 引言

冰蓄冷技术利用峰谷电价差异节省运行费用，实现电力的“削峰填谷”[1]，结合冷冻水大温差设计可提升单位冷冻水输送冷量，减少冷冻水输送能耗[2]。但降低供水温度将降低机组蒸发温度，造成机组效率下降，为寻求两者的平衡，国内学者从冷冻水供水温度优化角度进行了研究[3～6]，然而由于空调系统设备众多、管路复杂，大部分的研究仍处于理论阶段，工程的应用较少。

模糊控制具有适应非线性、时变系统的特点，不需要精确的数学模型，通过对现场经验的学习，就能获得较好控制效果[7]。基于模糊控制的特点，本文提出了基于模糊推理的冰蓄冷空调系统冷冻水供水温度设定方法，并引入变论域思想，通过变论域模糊推理实现冷冻水供水温度的自寻优，满足舒适性的同时减少系统能耗，并成功实现工程化应用。

1 变论域模糊推理

1.1 模糊推理

模糊推理理论是根据输入的模糊前件及模糊条件语句，经过模糊关系的合成运算得到输出量的数学运算过程。模糊条件语句是一种模糊蕴涵关系，表示由A到B的模糊推理过程。模糊推理按照输入前件维数可分为一维，二维及多维模糊推理。最常见的二维模糊推理结构如图1 所示，其中：Ke1和Ke2是前件输入的量化因子，Ku是模糊推理输出的比例因子。

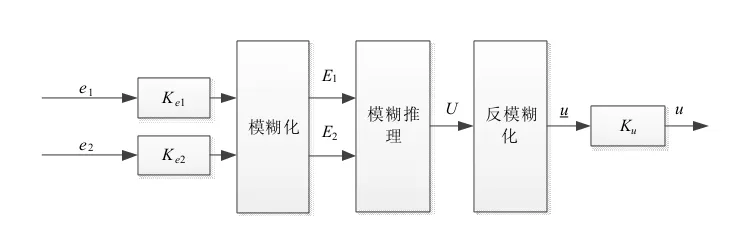
图1 二维模糊推理结构图

模糊推理是模糊控制算法的核心，它根据模糊系统的输入和模糊推理规则，经过模糊关系合成和模糊推理合成等运算，得出模糊系统的输出，最终经过反模糊化计算得到最终的控制输出结果。模糊推理应用的是广义前项推理，该推理过程是基于模糊逻辑中的模糊推理算法及模糊推理规则来进行的。

常用的模糊推理方法有扎德法和Mamdani 法。

1.2 变模糊论域思想

在模糊推理过程中，论域的划分对推理结果具有很大影响。尤其对于空调负荷、环境参数这种逐时变化区间较大的变量，使用单一的论域很难获得良好的推理结果，为了解决这一问题，李洪兴教授在 1999 年发表的题为《变论域自适应控制模糊器》的论文中提出了变论域的思想[8]。其通过调整量化因子Ke和比例因子Ku的办法来实现变论域，即通过伸缩因子α来对量化因子和比例因子进行修改，使得模糊控制过程平滑和连续。

变论域的思想为，对于某给定的模糊控制器，其输入输出论域分别为X=[-E，E]，Y=[-U，U]，引入一个函数α：→ [0,1],x|→α(x)，并且如果该函数具有对偶性、保零性、单调性、协调性、正规性的特性，则称α为论域X的伸缩因子。引入伸缩因子后即可对输入输出的论域进行压缩和膨胀，从而实现变论域模糊控制[8]。

1.3 时间轴自然分段变论域

在冷冻水供水温度寻优时，利用伸缩因子来实现变论域变得无法操作，这是空调系统的负荷或环境参数本身具有时变的特性，例如早晚温度自然存在差异，对于同样的温度数值26 ℃，在5:00 时属于高温，但在10:00 时属于正常温度，甚至是低温，要用可描述的函数来拟合伸缩因子非常困难。

然而，正因为负荷和环境温度有时变的特性，利用时间轴进行论域的自然分段则变得易于操作。如图2所示为某地区七月连续一周的逐时室外温度曲线。可以看出，虽然一周中每天某一时刻温度均不相同，但是每日逐时温度变化趋势是相似的，因此，对于每个时刻的温度值，是在一定范围内波动的，利用时间轴进行论域的自然分段，规划各个时间点对应的论域即可实现变模糊论域。同理，可利用时间轴实现负荷的变模糊论域。

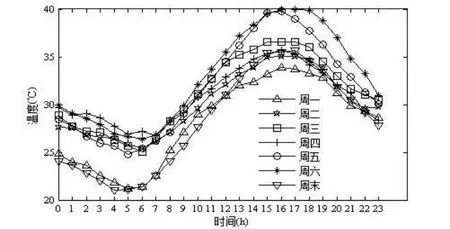
图2 某地区七月某周逐时室外温度曲线

时间轴自然分段变论域的实现方式则可表述为式1-1：

其中：X为模糊数学量；t为所处的时刻，Ti，i=1，…，n为按n个时段对每日24 小时进行分割的时间坐标，例如以 1 小时为周期进行分割，则Ti对应每个整点时刻 1:00、2:00、…、24:00；Eid，i=1，…，n为划分出的每个时间段内X的论域下限，Eiu，i=1，…，n为划分出的每个时间段内X的论域上限。

2 冷冻水供水温度设定

2.1 模糊推理前件计算

根据运行经验，影响冷冻水供水温度最重要的因素为室外环境和制冷负荷，因此，本文选择这两个参数作为模糊推理前件，其中，室外环境最重要的参数为室外温度和湿度，为便于计算，以室外空气焓值作为室外环境的参数指标。

根据空气焓值计算公式有：

其中：H为空气焓值，单位为kJ/kg干空气，t为空气温度，单位为℃，d为空气含湿量，单位为kg/kg干空气。

由于空调系统是闭式系统，根据能量守恒定律，冷冻水供回水热量的变化就是空调系统的换热量，即是中央空调系统的负荷。

根据热量计算公式有：

其中：Q为换热量即空调负荷，单位为 kJ/s，C为水的比热容，为4.2kJ/(kg· ℃)，q为流体流量，单位为kg/s，Δt为冷冻水供回水温差，单位为℃。

2.2 模糊前件变论域制定

模糊前件的论域以时间轴进行自然分段，本文以小时为单位分为24 段，即每个时刻设置独立的论域。在确定论域时，可将模糊前件划分为[负大，负中，负小，零，正小，正中，正大]等多个模糊子集，变论域的重点在于划分各个时刻下的论域大小，并确定每个模糊子集的隶属度函数。

在确定各时刻下论域的大小时，采用统计学的概率密度函数回归计算的方法，通过回归出期望和标准差值，即可确定在该时刻下的论域区间。以某大型公用建筑在每天10:00 的空调负荷为例，其历史统计数值如表1 所示：

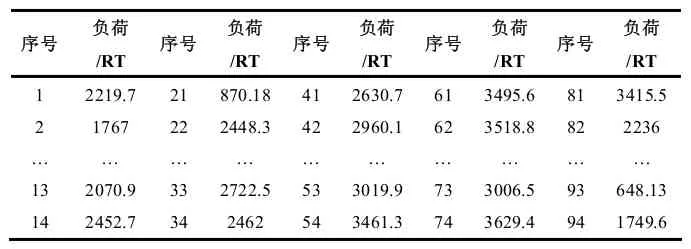
表1 某大型公用建筑每日10:00历史空调负荷统计表

将历史统计数据进行正态分布概率密度函数的回归计算 [9]，在0.95 置信水平下回归得到的期望和标准差分别为2552.8 和866.6，因此可画出该公用建筑在每日10 点空调负荷的概率分布曲线如图3 所示。

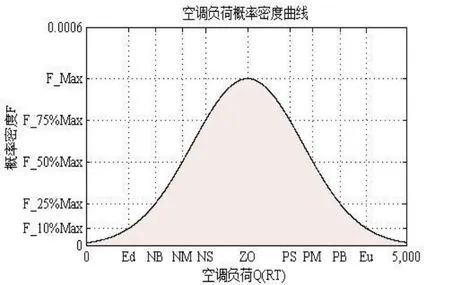
图3 10:00 空调负荷概率密度函数曲线

可以看出，通过对空调负荷进行统计回归后，即可画出空调负荷在10:00 时段的概率密度曲线，并且由于采用了正态分布的模型进行回归，回归得到的概率密度函数为式（4）：

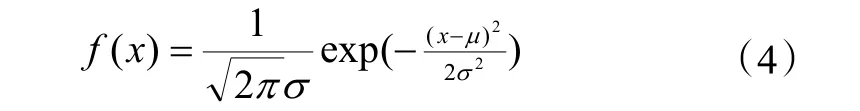
同样的，室外空气焓值在某时刻的概率密度函数也可以通过正态分布概率密度函数回归计算得到。

本文的设置方法为，首先获得期望所对应的概率密度F_Max，然后取10%F_Max 的概率密度所对应的变量值为论域区间，并分别取 25%、50%、75%F_Max的概率密度所对应的变量值为各模糊子集的隶属度中心。在得到论域和各模糊子集的隶属度中心后，采用三角型隶属度函数进行模糊处理，实现模糊前件的变论域模糊化处理。

2.3 冷冻水供水温度模糊推理

由于一天中每个时刻的室外空气焓值H和空调负荷Q的历史统计均值不同，因此冷冻水供水温度Ts的理论值也应随时间变化而变化。

为防止冷冻水供水温度Ts在同一时刻出现较大变化，并方便制定模糊推理规则，在做模糊推理时不宜直接计算出Ts数值，应采用基准温度+个体偏差的方式进行Ts数值的计算，即：

其中：Tsi为第i时刻冷冻水供水温度的基准值，可根据历史运行数据统计分析获得，单位为℃；ΔTsi为第i时刻由模糊推理得到的当前时刻Ts相对于基准值的个体偏差，单位为℃。

在进行偏差 ΔTsi的推理时，根据运行经验，当i时刻H和Q均较高时，为保证供冷量应适当减少Ts设定值；当H和Q均较低时，为避免系统能源浪费可适当增加Ts设定值；当H和Q偏离方向不一致时，由于负荷Q是直接反应对供冷的需求，偏差的偏离方向应向Q倾斜，因此，基于以上规则可指定模糊推理表如表2 所示。

表2 Δ Tsi模糊推理规则表

经过推理得到的偏差 ΔTsi经过反模糊化处理后，与基准温度Tsi求和即可得到最终的冷冻水供水设定温度Ts。

3 工程实例

3.1 工程概况

我国某大型交通枢纽制冷站采用冰蓄冷技术，系统冷冻水采用大温差小流量设计，供回水设计温度为2 ℃/14.5 ℃。

在实际运行中，依据多年运行经验，需要将系统回水温度控制在12 ℃左右，以确保空调末端设备能正常完成降温、除湿功能的同时，降低制冷站机组能耗和输送能耗。

由于该交通枢纽空调系统较庞大，运行人员为了保障末端用能需求，只能适当降低冷冻水供水温度，导致回水温度整体偏低。如图4 所示为2018 年7月某星期该交通枢纽站冷冻水供回水温度曲线。可以看出，为了保障末端用能需求，冷冻水供水温度设定值较低，导致回水温度基本在 12 ℃以下，其回水温度平均值为10.49 ℃，这意味着供水温度设定值整体偏低，具有一定的节能优化空间。

图4 某交通枢纽2018 年冷冻水供回水温度曲线

3.2 现场应用效果验证

为实现该交通枢纽冷冻水温度的自动调节，2 019年采用本方法制定了冷冻水供水温度自寻优策略，整体计算流程如下：

1）模糊推理前件制定

根据本文 2.1 节计算公式计算室外空气焓值H和空调负荷Q。

2）制定模糊变论域

根据本文 2.2 节的变论域制定方法进行H和Q在各时刻下的论域统计计算。在本案例中，按时间轴以小时为单位划分为 24 个时刻，各时刻下H和Q计算所得的变论域参数表部分示例如表3 所示，采用三角型隶属函数进行模糊化处理。

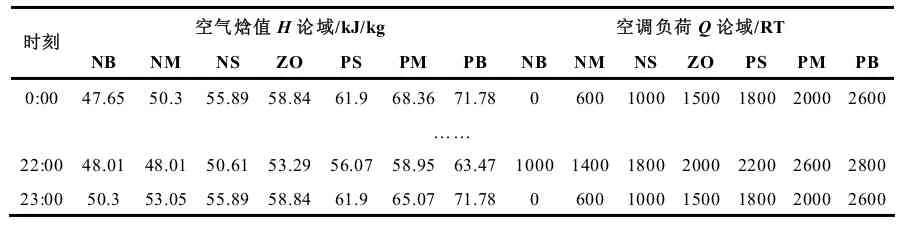
表3 H 和Q 变论域示例表

3.3 模糊推理

根据本文 2.3 节的模糊化推理方法进行冷冻水供水温度计算。需要注意的是，为避免由于Ts设定过于频繁造成系统波动，采用周期设定的方式进行寻优，即每隔固定周期进行一次参数寻优，在本案例中寻优周期为1 小时。

利用上述方法及表 2 制定的规则进行模糊推理，2019 年7月某星期冷冻水供回水温度及模糊推理设定温度曲线如图5 所示。

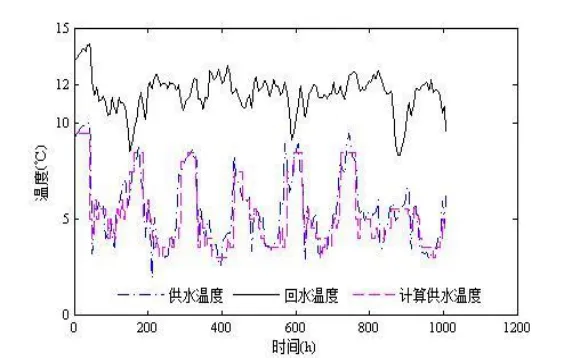
图5 某交通枢纽2019 年冷冻水供回水温度曲线

由图5 可以看出，使用本方法后，通过合理调整冷冻水供水温度，可将冷冻水回水温度控制在 12 ℃左右，实际上，图5 中冷冻水回水温度平均值为11.56 ℃，与2018 年同期运行数据相比冷冻水回水温度提升了1 ℃。同时，采用本方法后冷冻水供水温度平均值为5.54 ℃，而2018 年冷冻水的平均供水温度为4.88 ℃，可以看出，采用本方法后在维持冷冻水回水温度接近于设定值的同时，提高了冷冻水平均供水温度，有利于系统整体性的节能。对比数据表明，采用本方法可以有效实现冷冻水供水温度的自寻优，在满足负荷需求的同时将回水温度控制在设定值附近，可提升蒸发器平均温度，平衡系统制冷能耗和输送能耗，降低系统整体能耗。

4 结语

冰蓄冷空调系统具有出水温度低的特点，结合大温差小流量的供冷方式可有效减少系统输送能耗，最大化发挥冰蓄冷系统优点，实现削峰填谷。为解决冷冻水供水温度自寻优的问题，本文提出了基于模糊推理的冷冻水供水温度设定方法，并针对坏境参数、空调负荷等具有时变的特点，引入了变论域的概念，以时间轴自然实现变论域划分，同时通过统计分析手段实现各项参数的整定，具有较好的可操作性，方便各工程现场使用。工程应用证明，采用本方法进行冷冻水供水温度寻优，有利于空调系统质调和量调的结合，实现对冷冻水回水温度的精确控制，减少系统整体能耗和运行费用。