基于等效矢量模型的双光楔逆解算法研究

冯建鑫，王 强，王雅雷，胥 彪

（南京航空航天大学 航天学院，江苏 南京 211106）

1 引 言

高精度光束指向控制技术在空间光通信、红外对抗、激光雷达等工程领域中有广泛应用[1-2]。相较于传统万向架、复合轴等光束指向机构，基于双光楔结构的光束指向机构具有小型化、响应快速、成本低廉、结构紧凑等特点，该技术在光束扫描、远距离目标瞄准跟踪等方面展现出广泛应用前景[3]。

双光楔结构应用中的一个基本问题是根据出射光线的方向，求解两棱镜的旋转角度[4-5]，但目前对该问题的研究依然存在一些不足之处。Amirault采用两步法求解双棱镜的转角[6]，Li在两步法的基础上建立一个三阶表达式来求解反问题[7]，这两种算法虽然计算时间极短，但很难满足激光通信的精度要求。Tao提出了一种基于阻尼最小二乘法的迭代求解方法（ISD），该方法提高了计算精度，但是计算量剧增，导致计算时间过长，不适用于实时跟踪领域[8]。Li提出了一种查表方法，通过建立由棱镜转角(θr1,θr2)和扫描点坐标(xrp,yrp,zrp)组成数据库的方式，将棱镜转角从计算求解转换成查表获得；随着转角分辨率的提高，其计算精度不断提高，但所需内存也急剧增大，使得硬件成本增加[9]。Li还提出用正演方法进行反复迭代求解的方法，通过迭代使用两步法的思想不断减少扫描点与目标点偏差值，该方法大幅提高了计算精度，计算时间比ISD更小，但依然不满足实时性要求[10]。周远利用一阶近轴理论研究双光楔反向解，该方法计算量小，但实验结果存在偏差，不满足高精度工程应用要求[11]。

为了进一步提高双光楔反解算法的计算精度，同时减少计算时间，本文在正演迭代法的基础上结合双光楔等效矢量模型，提出一种等效矢量迭代反解算法。该方法利用矢量叠加的方式求解出射光线的位置坐标，避免多次计算，减少了计算量，缩短了计算时间。

综上所述，本文首先利用斯涅耳定律以及双光楔对入射光线的偏转作用，说明了两步法的原理；再利用反复迭代、不断逼近的思想介绍了正演迭代法的基本过程，解决了两步法精度不足的问题；最后引入光楔等效矢量模型，将该模型与正演迭代算法相结合，提出等效矢量迭代算法，该算法不仅计算精度高，而且计算量不大，计算时间大幅缩短。

2 双光楔原理

当光线发生折射时，入射光线和折射光线的方向分别由单位光线矢量sin和sout表示，单位向量N表示界面法线方向，界面两侧不同材料折射率分别为nin和nout，向量形式的斯涅耳定律可以表示为[12]

为了更好地说明光线在双光楔系统的折射情况，建立如图1所示的结构示意图。双光楔系统由两个楔角α、折射率n以及最薄端厚度d0均相同的棱镜组成，两个棱镜的平面向外，垂直于Z轴，其中每个棱镜的主截面位于ZOY平面上，最薄一端朝向Z轴正方向。记双光楔入射光线为A0，出射光线为Af，视场坐标轴的原点为Op，棱镜转角为θ1=θ2=0°时为初始状态，棱镜绕Z轴逆时针旋转设为正方向，两个平面之间距离为D1，棱镜2平面到视场距离为D2。

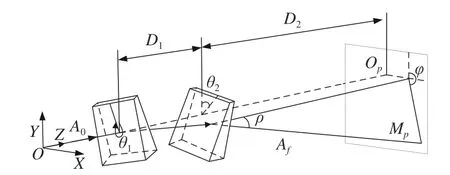
图1 双光楔系统坐标系示意图Fig. 1 Schematic diagram of the coordinate system of Risley-prism

图2 为双光楔平面光路图。棱镜界面法向量为Nj（j=1,2,3,4），各个折射光线表示为单位矢量sj。记棱镜1出射点M1(0, 0,d0)、棱镜2入射点M2(xm,ym,D1+d0)、棱镜2出射点为M3(xn,yn,D1−2d0)，由于d0远小于D1与D2，因此可以简化为M3(xn,yn,D1)。出射光线打到视场上的扫描点为p(xp,yp,D1+D2)。

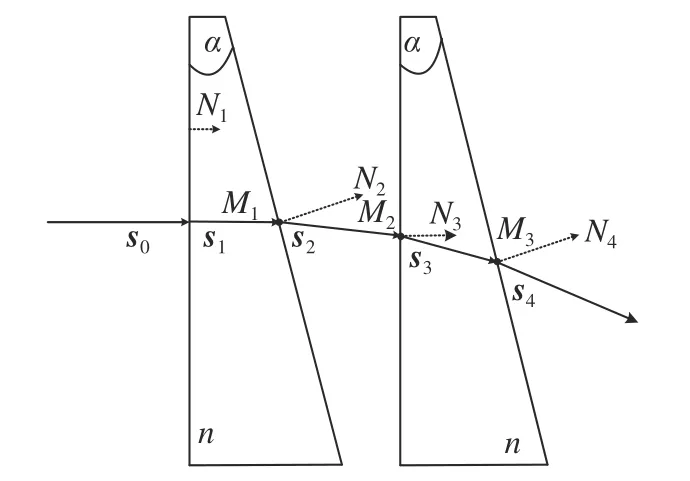
图2 界面处光线折射光路图Fig. 2 Light path diagram of light refraction at the interface

根据式（1）和图2的光路图，出射点M3(xn,yn,D1)和扫描点Mp(xp,yp,D1+D2)分别表示为

出射光线与Z轴正方向的偏差角定义为俯仰角ρ，投影在视场上的出射光线与Y轴正方向的夹角定义为方位角φ。俯仰角ρ和方位角φ的计算公式分别为

3 双光楔逆解算法研究

3.1 两步逆解法

当出射光线的俯仰角和方位角确定时，便可以借助两步法反解棱镜旋转角度[13]，具体步骤为：

（1）棱镜1保持静止，即θ1=0，旋转棱镜2直到出射光线的俯仰角ρ等于给定光线的俯仰角，由式（4）～式（6）得到此时棱镜2的转角，利用斯涅耳定律求解此时出射光线的方位角φ0，即

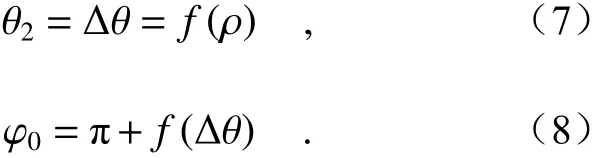
（2）两个棱镜同时旋转φ−φ0角度，使得出射光线与给定光线的方位角相等。两个棱镜转角分别为

由于入射光线经过多次折射后，棱镜2出射面的出射点不固定，无法只根据给定点得到出射光线矢量，因此两步法精度较低[10,14]。

3.2 正演迭代法

本文利用迭代求精思想使计算得到的出射光线逐步逼近期望出射光线，再利用两步法求解棱镜旋转角度，以此来提高计算精度。该算法步骤如下:

（1）给定目标点Mp(xp,yp,D1+D2)及棱镜2出射面上的初始出射点M3(0, 0,D1)；

（2）根据出射点和给定点得到出射光线矢量，再根据两步法求解棱镜转角近似解θi=(θ1i,θ2i)；

（3）将棱镜转角代入式（2）和式（3）中，更新此时出射点M3(xni,yni,D1)和扫描点pi(xni,yni,D1+D2)；

（4）计算此时扫描点与目标点之间误差值，即

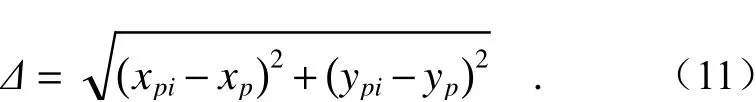
给定允许误差阈值ε，若Δ<ε，旋转角θi=(θ1i,θ2i)的解可视为最终结果。如果没有，转到步骤（2）。

正演迭代法相较于两步法提高了计算精度，但每次迭代需要计算多次斯涅耳定律，导致计算量过大，计算时间过长，不满足高性能应用领域实时性要求。因此减少计算量和计算时间有重要研究意义。

4 等效矢量迭代法

本文通过研究光楔折射特性，将其等效成运动矢量，运用矢量叠加法求解出射光线位置矢量。该方法减少了计算量，且精度满足激光通信要求[15-16]。

4.1 光楔矢量模型

记棱镜入射光线和出射光线的夹角为δ，由式（12）可得：

当棱镜绕Z轴旋转时，出射光线在空间的轨迹是一个顶角为2δ的圆锥面。在垂直于Z轴并且与棱镜出射点相距l的位置建立一个平面直角坐标系，原点为Z轴在平面上的投影，此时出射光线在该平面的轨迹是一个半径为r的圆，如图3所示。

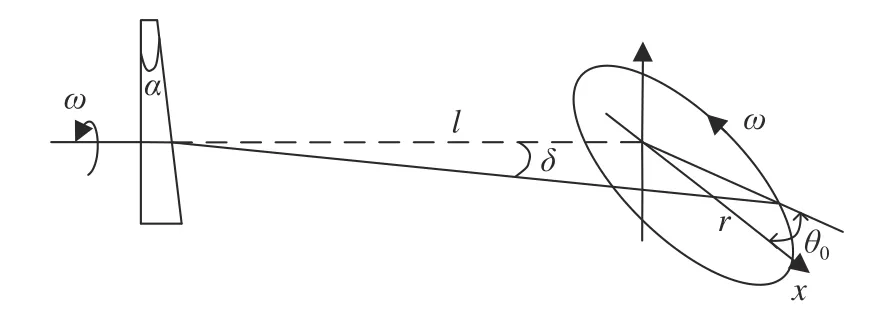
图3 旋转单光楔光路Fig. 3 Single rotating Risley-prism optical path

记出射光线与平面直角坐标系相交于A点，设棱镜位于初始位置时OA与x轴夹角为θ0，当棱镜旋转一定角度且转角为θr时，出射光线的方位角θ为

由式（12）可知，当棱镜折射率和顶角不发生改变时，δ为定值；由式（13）可知，出射光线的方位角由棱镜的旋转角度θr与初始方位角θ0共同决定。因此可以将棱镜等效成模长为δ，角速度为ω，初始相位为θ0的旋转矢量，如图4所示。

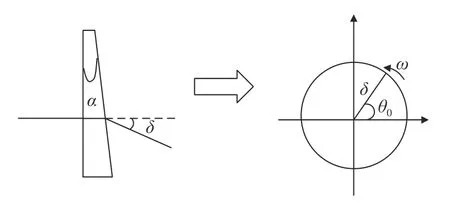
图4 旋转单光楔等效矢量模型Fig. 4 Equivalent vector model of the rotary single prism

4.2 基于等效矢量模型的逆解算法

4.2.1 双光楔等效矢量叠加算法

利用4.1节思路，将两个棱镜均等效成角速度为ω1、模长为δ的旋转矢量，初始相位分别为θ10、θ20，则两旋转矢量的相位分别为

根据两个旋转矢量的相位θr1和θr2可以确定出射光线的位置，如图5所示。由矢量叠加平行四边形法则可知，此时出射光线的俯仰角和方位角分别为

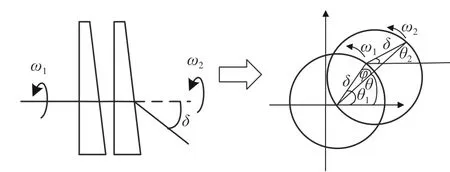
图5 旋转双光楔等效矢量模型Fig. 5 Equivalent vector model of the Risley-prism

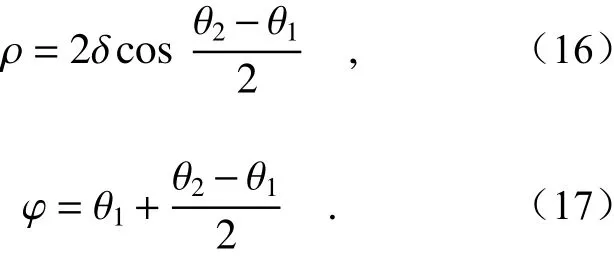
出射光线的位置由俯仰角与方位角确定，该方法把斯涅耳定律计算转换成简单的矢量叠加计算。

4.2.2 等效矢量两步逆解法

当出射光线的俯仰角与方位角确定后，利用两步法思路求解棱镜转角。

（1）棱镜1保持静止，即θ1=0，旋转棱镜2，直到出射光线的俯仰角ρ等于给定光线的俯仰角，此时由式（12）和式（16）可得棱镜2的旋转角度：

（2）同时旋转两个棱镜，使得出射光线与给定光线的方位角相等，此时棱镜1的旋转角度为

再由式（10）得到棱镜2的转动角度，即

两步反解算法的流程如图6所示。综上所述，基于等效矢量法的双光楔两步逆解法与前文的两步逆解法流程一致，但计算量大幅度减少。

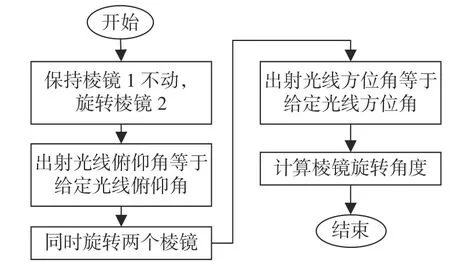
图6 两步逆解法流程图Fig. 6 Flow chart of two step inverse method

4.2.3 等效矢量迭代法

由于两步法本身存在缺陷，导致其精度较低，本文将正演迭代求精算法与等效矢量两步法相结合，以提高计算精度，等效矢量迭代法步骤如下：

（1）给定视场上的目标点Mp(xp,yp,D1+D2)，设棱镜2出射面的中心点为初始出射点N0(0, 0,D1)。

（2）出射光线矢量如式（21）所示，再由式（22）～式（24）求解ρ和φ，最后用两步法计算θi=(θ1i,θ2i).

（3）由于棱镜1入射平面的法向量与入射光线平行，入射光线方向不改变，即s1为(0, 0, 1)。由4.1节可知，棱镜1出射光线s2俯仰角ρs2为(n−1)α，方位角φs2为 θ1i+θ0，那么棱镜2入射点M2坐标为

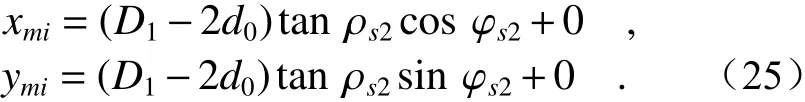
由平面光路图可知，根据M1和M2坐标可得到s2的矢量坐标，然后利用式（1）求解s3的矢量坐标及其俯仰角ρs3和方位角φs3。此时M3坐标为：

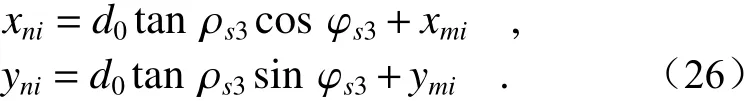
由于d0远小于D1与D2，因此可以将出射点坐标简化为M3(xni,yni,D1)。由式（16）～式（17）可得出射光线俯仰角ρ和方位角φ，此时扫描点pi坐标为：

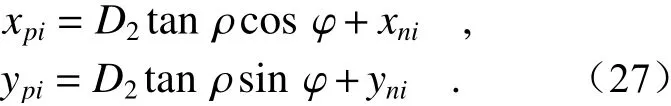
（4）计算此时扫描点与目标点之间偏差值：

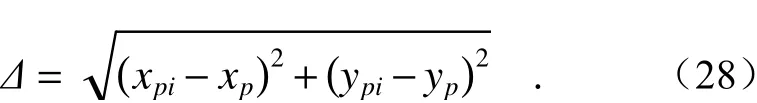
给定允许误差阈值ε，若Δ<ε，旋转角θi=(θ1i,θ2i)的解可视为最终结果。如果没有，转到步骤（2）。

图7为等效矢量迭代法的流程图。综上所述，等效矢量迭代法相比于正演迭代法虽然流程相同，但步骤（2）计算量大幅减少，步骤（3）仅计算一次斯涅耳定律，算法的整体计算量进一步降低，计算时间得到极大缩短。

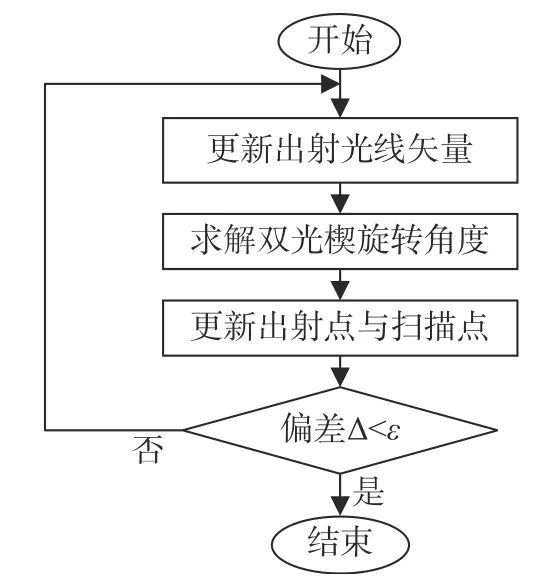
图7 等效矢量迭代法流程图Fig. 7 Flow chart of the equivalent vector iteration method

5 仿真与实验

5.1 计算精度比较

给定一个椭圆的目标轨迹，将其表达式设置为：

在轨迹上选取63个采样点，根据4组反解算法计算双光楔系统棱镜旋转角，再由棱镜转角求解相应扫描轨迹，误差为目标点与扫描点之间距离。

在Matlab2019环境下进行仿真实验，图8～11（彩图见期刊电子版）为模拟的扫描轨迹，并得到了偏差Δ和算法的解算时间，具体数值如表1所示。

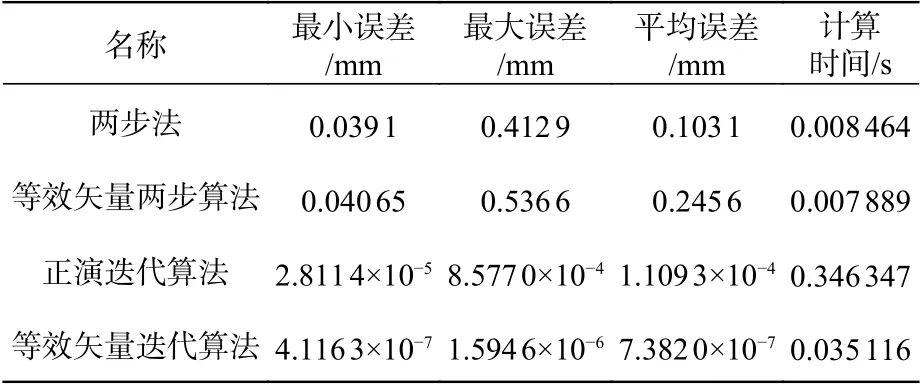
表1 4种逆解算法的结果比较Tab. 1 Comparison of the results of four inverse algorithms

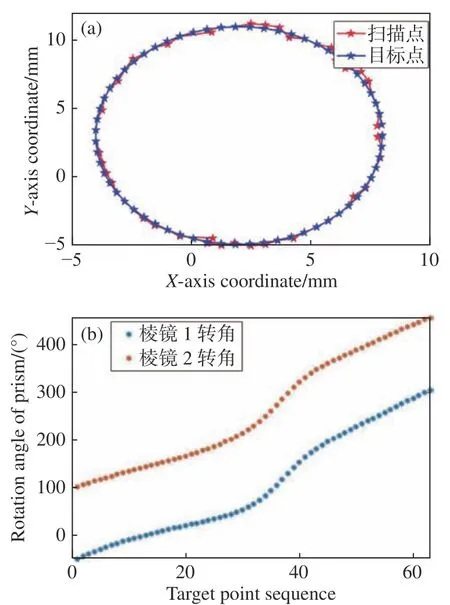
图8 两步法(a)目标轨迹、扫描轨迹与(b)棱镜转角Fig. 8 (a) Target trajectory and scanning trajectory and(b) rotation angle of prism for two-step method

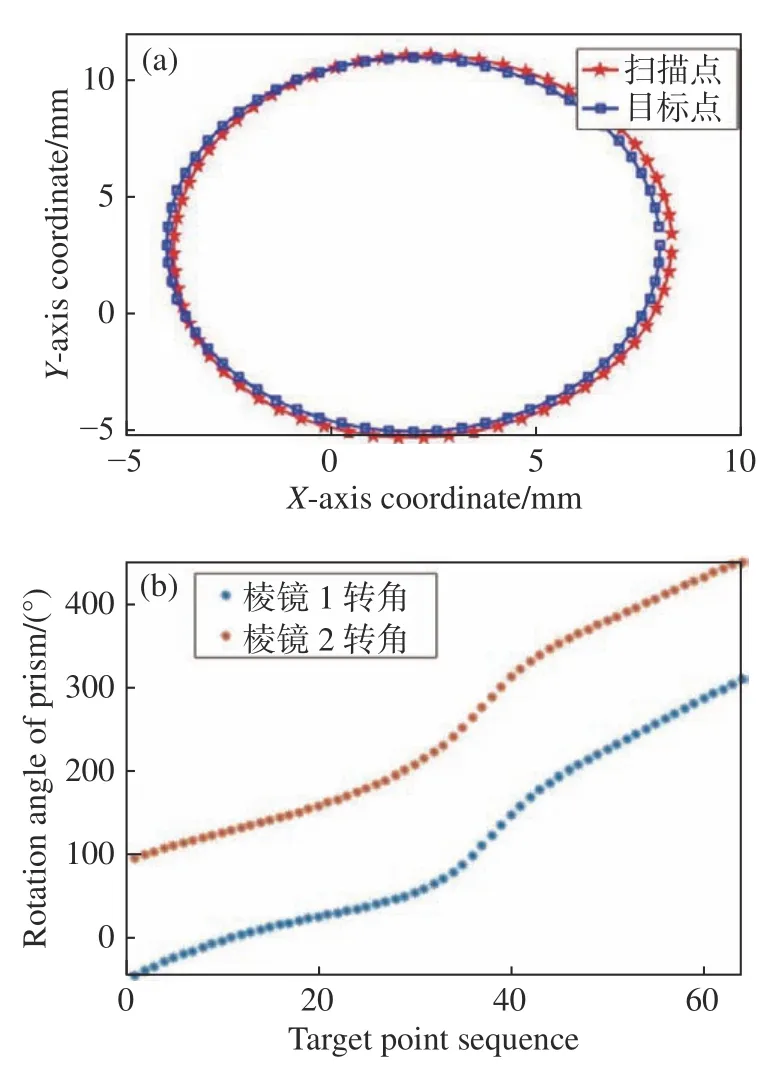
图9 等效矢量两步法(a)目标轨迹、扫描轨迹与(b)棱镜转角Fig. 9 (a) Target trajectory and scanning trajectory and(b) rotation angle of prism for equivalent vector two-step method

图10 正演迭代法(a)目标轨迹、扫描轨迹与(b)棱镜转角Fig. 10 (a) Target trajectory and scanning trajectory and(b) rotation angle of prism for forward iterative refinement algorithm

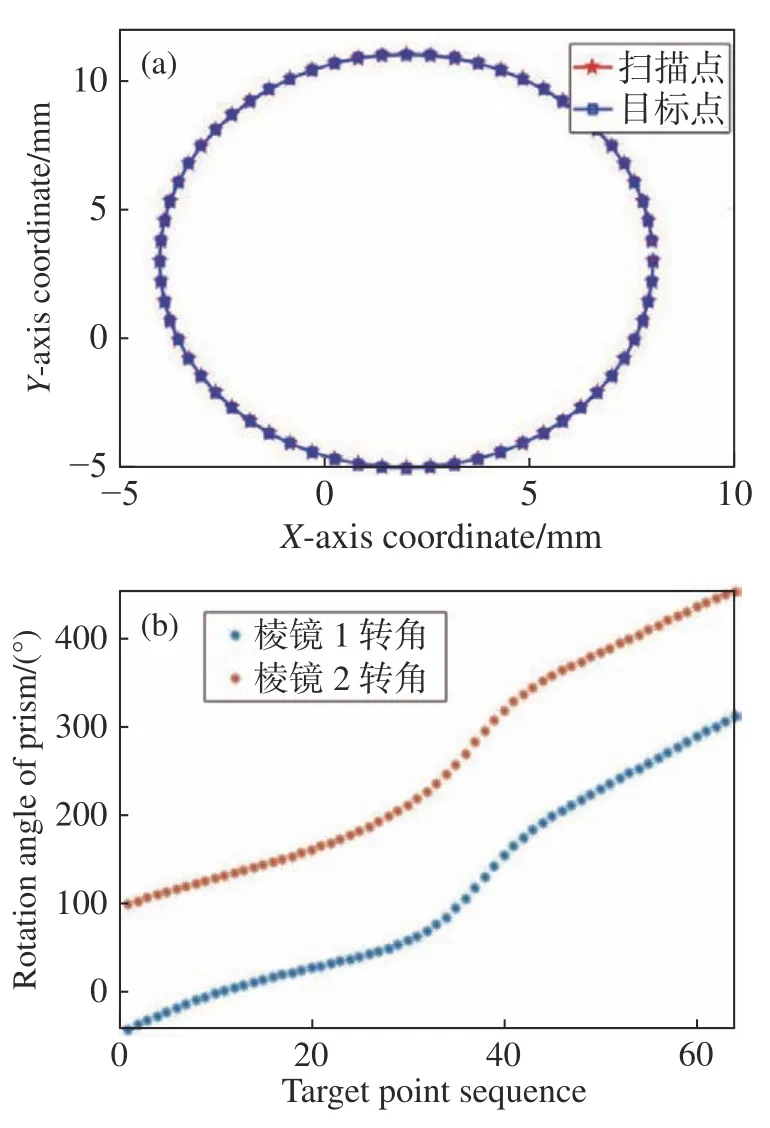
图11 等效矢量迭代法(a)目标轨迹、扫描轨迹与(b)棱镜转角Fig. 11 (a) Target trajectory and scanning trajectory and(b) rotation angle of prism for equivalent vector iteration method

5.2 逆解算法影响因素

为了研究两种算法的适用场合，需要分析不同因素对两种算法的影响。首先研究D2对两种算法的影响，引入相对精度R1=Δ1/D2和R2=Δ2/D2的概念。

图12（彩图见期刊电子版）为仿真实验图，蓝色实线为实际误差，对应左边y轴；红色虚线为相对误差，对应右边y轴。由图可知，两种算法的相对精度随着D2距离的增加而不断降低；在D2较小时，正演迭代法实际误差与相对精度的下降速度更大。综上所述，两种算法更适用于远距离扫描场合。

图12 D2对两种算法的影响。(a)正演迭代法；(b)等效矢量迭代法Fig. 12 Influence of D2 on two algorithms. (a) Forward iteration method; (b) equivalent vector iteration method

然后研究视场大小的影响。设给定椭圆轨迹为：

图13为通过增加a值大小使得视场角不断增大的仿真实验图，D2距离设为500 mm并保持不变。

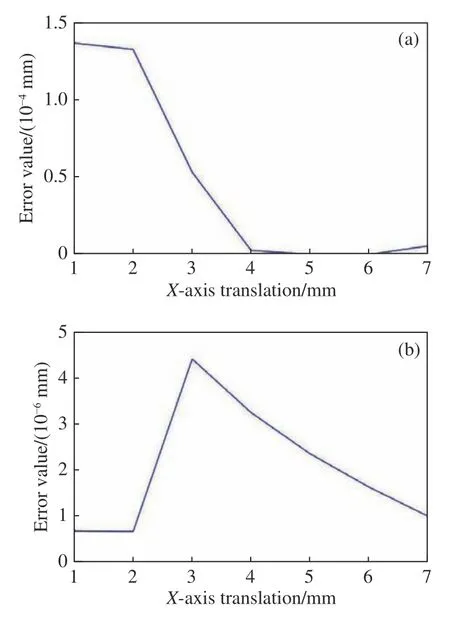
图13 视场角大小对（a）正演迭代算法和（b）等效矢量迭代算法的影响Fig. 13 Influence of angle of view on (a) forward interative refinement algorithm and (b) equivalent vector iteration method

由图13可知，等效矢量迭代法在距离原点较近时，误差值较小，并且存在一个尖峰使得误差值最大，但尖峰之后误差又会随a值增加而减少；正演迭代法实际精度在刚开始变化不大，但随着a值的增大而不断减少，呈明显下降趋势，并且在a值较大时，误差变化不明显。综上所述，正演迭代法在距离原点较远时计算精度更高，更适应于大视场的应用场合；等效矢量迭代法计算精度远小于正演迭代法，并且更适用于小视场的应用场合。

5.3 实验研究

本文选取4个点进行实验研究，分别运用正演迭代法与等效矢量迭代法求解棱镜旋转角度，测试两种算法在DSP芯片的计算精度与计算时间。本文选取的DSP类型为TI公司生产的TMS320F28335系列芯片，该芯片具有150 MHz的高速处理能力，具备32位浮点处理单元，实验装置图见图14。表2为DSP求解的具体数值。

表2 两种逆解算法的计算结果比较Tab. 2 Comparison of the results of two inverse algorithms

图14 DSP实验装置图Fig. 14 Experimental device

由于DSP芯片只有32位浮点处理单元，因此在进行相关计算时，必定会产生数据截断的现象，从而导致DSP上计算精度不如Matlab仿真环境，但是等效矢量迭代法的计算精度依然达到了10−5mm，基本满足高性能应用领域的计算精度要求。若使用更高级别芯片进行实验研究时，等效矢量迭代法精度更高，而计算时间随系统频率提升不断缩短。

6 结 论

近年来，双光楔系统的逆解问题得到了广泛地关注。本文通过研究常用的两步法和正演迭代求精算法之后，将两种算法与光楔等效矢量模型相结合，提出了基于光楔等效矢量模型的逆解算法。该算法通过简单的矢量叠加方式求解出射光线矢量坐标，使得计算量大幅度降低，缩短了计算时间；并且利用正演迭代求精的思想，使得扫描点逐步逼近目标点，极大地提高了计算精度。通过实验可知，正演迭代法和等效矢量迭代法的相对精度随着D值的增大而降低，因此这两种算法都更适用于远距离扫描应用场合，并且等效矢量迭代法的计算精度比正演迭代法高1～2个数量级；正演迭代法距离原点越远，其计算精度越高，因此该算法更适用于大视场的应用场合；而等效矢量迭代法在距离原点较近时其计算精度更高，因此更适用于小视场的应用场合。由DSP实验数据可知，等效矢量法的计算精度达到了10 μm级别，计算时间在0.1 ms以内，本文研究的等效矢量迭代法对基于双光楔结构的光束指向控制技术有重要意义。