天然气管网中一类新的压缩机功率拟合函数

马 越 寇彩霞

北京邮电大学理学院, 北京 100876

0 前言

近年来，中国天然气需求量不断增长、管道业务迅速发展,高效求解天然气管网系统运行优化问题越发重要。天然气管网系统运行优化问题通常以运行成本最低作为目标函数[1-2],压缩机功率作为运行成本的重要组成部分在整个优化过程中需要反复计算。对于大型天然气管网系统,完成一次运行优化问题的求解一般需要数十小时[3-4],而压缩机功率的计算量占绝大部分。因此,设法简化压缩机功率计算、减少该环节的计算量，对整个天然气管网系统运行优化尤为重要。

天然气管网系统中常用的压缩机有往复式压缩机和离心式压缩机。往复式压缩机功率计算较为简单,计算量小。离心式压缩机特性方程复杂,功率计算繁琐,但因其运行平稳、排量大、调节方便等优点而被广泛应用于天然气管网系统[5-6],本文主要对离心式压缩机的功率计算进行研究。在天然气管网系统运行优化问题的求解过程中,需要根据压缩机的入口气体流量、入口气体压力、出口气体压力及入口气体温度等变量计算压缩机功率。压缩机功率的传统计算方法需要利用压缩机特性方程、相关的气体热力学公式以及气体状态方程等,迭代求解压缩因子、压缩机转速等多个参数,计算过程极其复杂,计算量大[7]。

为提高计算效率、加快求解速度,Wu Suming等人[8]提出了1种基于拟合函数的压缩机功率近似计算方法。其思想是将压缩机功率与压缩机入口气体流量、入口气体压力和出口气体压力之间的关系拟合为1个显式函数,以代替压缩机功率的传统计算方法。但该压缩机功率拟合函数未考虑压缩机入口气体温度变化,适应性较差。为增强压缩机功率拟合函数的适应性,熊浩云等人[7]将压缩机入口气体温度作为自变量,对Wu Suming等人的压缩机功率拟合函数加以改进,精度明显提高,但对于实际应用仍需进一步提高精度。为满足实际应用需求,进一步提高压缩机功率拟合函数的精度,本文提出了3个新的压缩机功率拟合函数。

1 传统计算方法

离心式压缩机功率传统计算方法的主要思想是根据压缩机入口气体流量、入口气体压力、出口气体压力和入口气体温度等变量,结合压缩机特性方程、相关的气体热力学公式及气体状态方程,利用迭代法计算压缩机功率。

1.1 压缩机特性方程

压缩机特性方程是计算压缩机功率的依据[9-10],对于离心式压缩机,常用的变转速特性方程有压头—流量—转速方程、效率—流量—转速方程、喘振流量—转速方程和滞止流量—转速方程,见式(1)～(4)[11]:

(1)

(2)

Q=c1n2+c2n+c3

(3)

Q=d1n2+d2n+d3

(4)

1.2 气体状态方程

常用气体状态方程有Van den Waals[12]、RK[13]、SRK[14]、PR[15]和BWRS[16]等。本文采用精度较高的BWRS方程,见式(5):

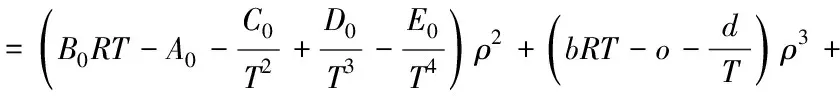
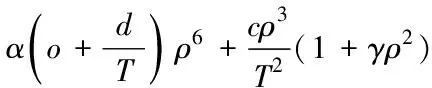
(5)

1.3 压缩机功率的传统计算方法

下面介绍天然气在离心式压缩机中增压多变过程的主要计算公式。表1[17]给出了随状态变化各点上的可压缩性函数X、Y，最大与最小等熵指数比kmax/kmin所规定的精确度。当气体状态满足表1所列的范围时,可以近似使用理想气体的相关计算公式[17-18],见式(6)～(9):

表1 用于状态变化简化计算的允许偏离表

(6)

(7)

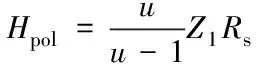
(8)

(9)

如果给定的真实气体特性超出表1所列极限值,确定多变指数时应考虑压缩过程中可压缩性系数的变化,故对于真实气体的相关计算公式见式(10)～(14)[17]:

(10)

(11)

(12)

(13)

(14)

根据压缩机特性方程式(1)～(4)、气体状态方程式(5)、上述方程式(6)～(14)及其推导出的其他气体物性参数,可以通过迭代计算得到压缩机出口气体温度T2和压缩机功率N。

2 拟合函数法

在天然气管网系统运行优化问题中,采用传统方法计算压缩机功率非常复杂、耗时。因此,本文考虑采用基于拟合函数的压缩机功率近似计算方法,将压缩机功率与压缩机入口气体流量、入口气体压力、出口气体压力和入口气体温度之间的关系拟合为一个显式函数。使用该拟合函数计算压缩机功率以降低计算成本、加快求解速度。目前已有的压缩机功率拟合函数均存在精度较低、适应性较差的缺点,不能满足实际应用需求。故本文在已有的研究基础上,提出了3个精度更高的压缩机功率拟合函数见式(15)～(17):

(15)

(16)

(17)

3 拟合函数精度对比

以中国某天然气管网系统中配置的3种型号压缩机为实验对象,检验3个新的压缩机功率拟合函数的数值表现效果。

实验中各自变量取值范围如下：380 m3/s≤入口气体体积流量Q≤591 m3/s，6.5×106Pa≤入口气体压力p1≤8.5×106Pa，8.5×106Pa≤出口气体压力p2≤1.0×107Pa，278.15 K≤入口气体温度T1≤298.15 K。相关参数取值如下:压缩机机械效率ηm为0.98,转速范围为3 120～4 800 r/min,压缩机特性方程系数见表2。天然气各成分摩尔含量为：甲烷96.30%、乙烷1.95%、丙烷0.16%、正丁烷0.03%、异丁烷0.03%、正戊烷0.01%、异戊烷0.01%、正己烷0.03%、二氧化碳0.66%、氮气0.82%。

表2 压缩机特性方程系数表

1)选取样本点[7]。在各自变量定义域内等距取10个点,组合得到10 000个工况数据,去掉不在可行域中的工况数据,得到4 904个可行工况数据。用传统计算方法计算可行工况数据对应的压缩机功率,得到4 904个样本点。

2)确定拟合系数。对于上述样本点,应用matlab中的非线性拟合函数nlinfit确定的拟合系数,结果见表3。

表3 的拟合系数表

Tab.3 Coefficients of

表3 的拟合系数表

拟合函数型号拟合系数值A1A2A3A4A5A6A7A8A9g1new14.830 9×1060.025 2-943.447 3530.321 6-0.004 5-0.031 33.246 0×10-482.619 7-2.669 1×10-427.320 0×105-0.002 5-168.922 593.807 60.008 6-0.008 41.667 8×10-434.625 0-1.567 1×10-431.436 9×106-0.009 4-199.774 381.779 80.001 7-0.001 44.231 6×10-489.675 4-3.914 1×10-4拟合函数型号拟合系数值B1B2B3B4B5B6B7B8B9g2new1312.183 01.807 4×10-6-0.074 90.033 21.763 6×10-7-1.694 4×10-63.233 5×10-491.291 4-2.665 5×10-4229.949 9-2.016 2×10-7-0.022 90.017 31.458 8×10-6-1.296 7×10-61.657 4×10-435.544 6-1.554 5×10-43103.078 6-7.990 5×10-7-0.050 30.032 13.021 6×10-6-2.196 3×10-64.221 5×10-494.940 9-3.905 6×10-4拟合函数型号拟合系数值C1C2C3C4C5C6C7C8C9g3new1245.424 19.833 2×10-7-0.043 50.006 61.160 7×10-6-1.927 5×10-63.313 3×10-490.796 9-2.534 7×10-4224.165 69.597 0×10-8-0.012 70.006 73.804 6×10-7-4.549 2×10-71.668 0×10-435.367 1-1.569 3×10-4381.726 63.651 4×10-7-0.027 20.009 5-1.858 0×10-7-0.755 9×10-74.226 6×10-494.663 5-3.914 0×10-4

其次,对不同压缩机功率拟合函数的精度进行对比。

1)选取测试工况数据。在各自变量定义域内随机取10个点,组合得到10 000个工况数据,去掉不在可行域中的工况数据,得到3 203个可行工况数据作为测试工况数据。

2)计算误差。分别采用传统计算方法和拟合函数法计算每个测试工况数据对应的压缩机功率并计算两者之间的最大相对误差与平均相对误差。

实验结果见表4。由表4可知，本文提出的3个新压缩机功率拟合函数的计算精度较其余4个压缩机功率拟合函数的计算精度均有明显提高。与中精度最高的相比,本文提出的3个新压缩机功率拟合函数的最大误差减小量最高可达59.56%,平均误差减小量最高可达74.36%,具体结果见表5。

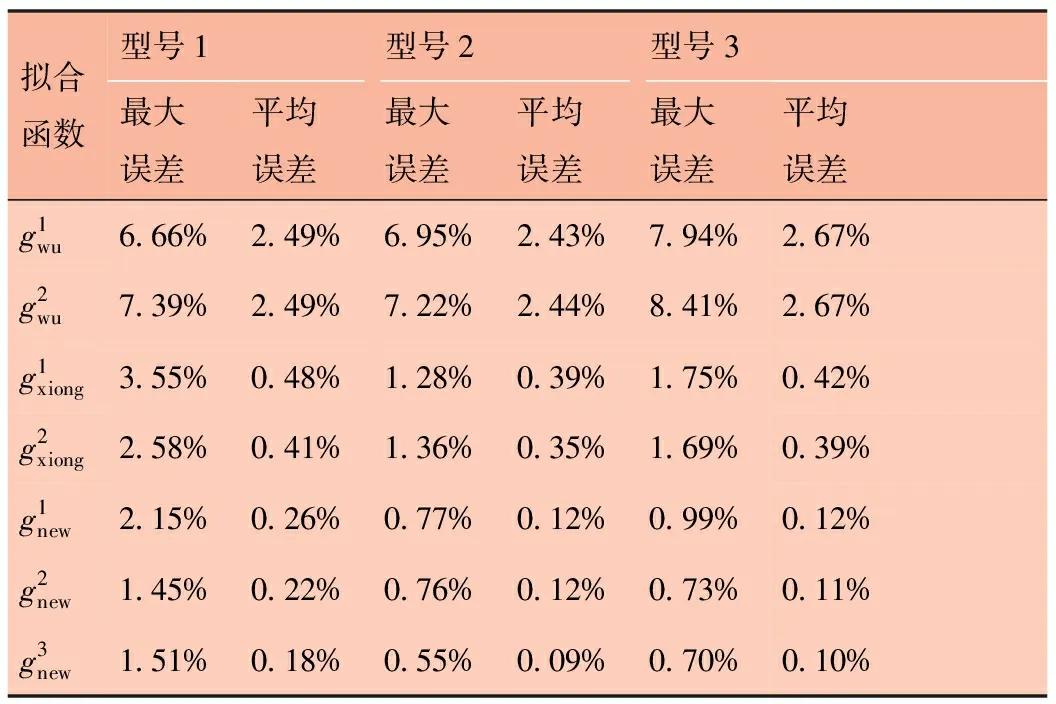
表4 各压缩机功率拟合函数的精度测试对比表

表5 的误差减小量对比表

Tab.5 Comparasion of error reduction of

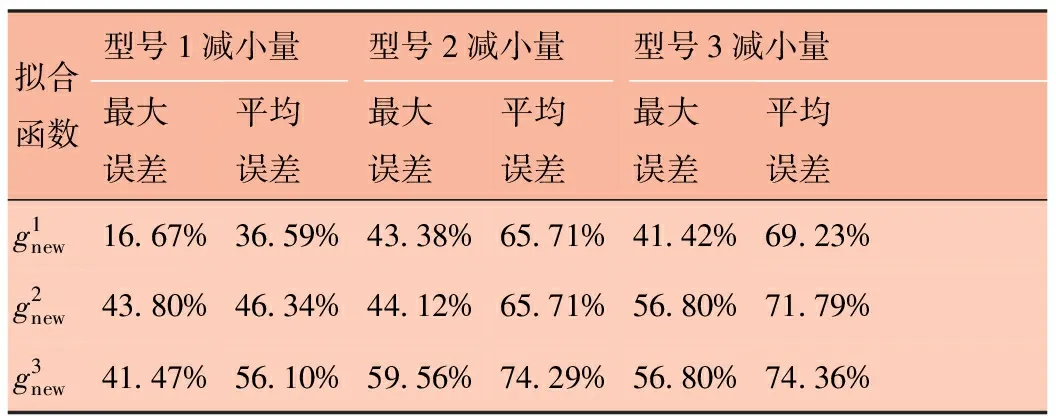
表5 的误差减小量对比表

拟合函数型号1减小量型号2减小量型号3减小量最大误差平均误差最大误差平均误差最大误差平均误差g1new16.67%36.59%43.38%65.71%41.42%69.23%g2new43.80%46.34%44.12%65.71%56.80%71.79%g3new41.47%56.10%59.56%74.29%56.80%74.36%

4 案例分析

本节使用拟合函数法代替压缩机功率的传统计算方法,应用于一小型虚拟天然气管网系统进行运行优化求解,并与传统计算方法进行对比,其中虚拟管网模型见图1。3台压缩机型号分别为1、2、3,每条管道长 20 km。首个压缩机入口气体压力为7 MPa、入口气体温度为288.15 K,每个压缩机允许的最低入口气体压力和最高出口气体压力分别为6.5 MPa和10 MPa。实验中采用动态规划算法对该天然气管网系统在多种流量下的运行优化问题进行求解[19-20],压缩机出口压力离散步长取0.01 MPa。

图1 虚拟天然气管网系统图Fig.1 Virtual gas pipeline network

所有实验均在matlab 2015b中编写,并在内核2.10 GHz、内存12 GB的笔记本电脑上运行。为减弱CPU性能对实验结果的影响,对于每种流量方案均进行了20次实验,计算时间取其平均值，实验结果见表6。由表6可得以下四点。

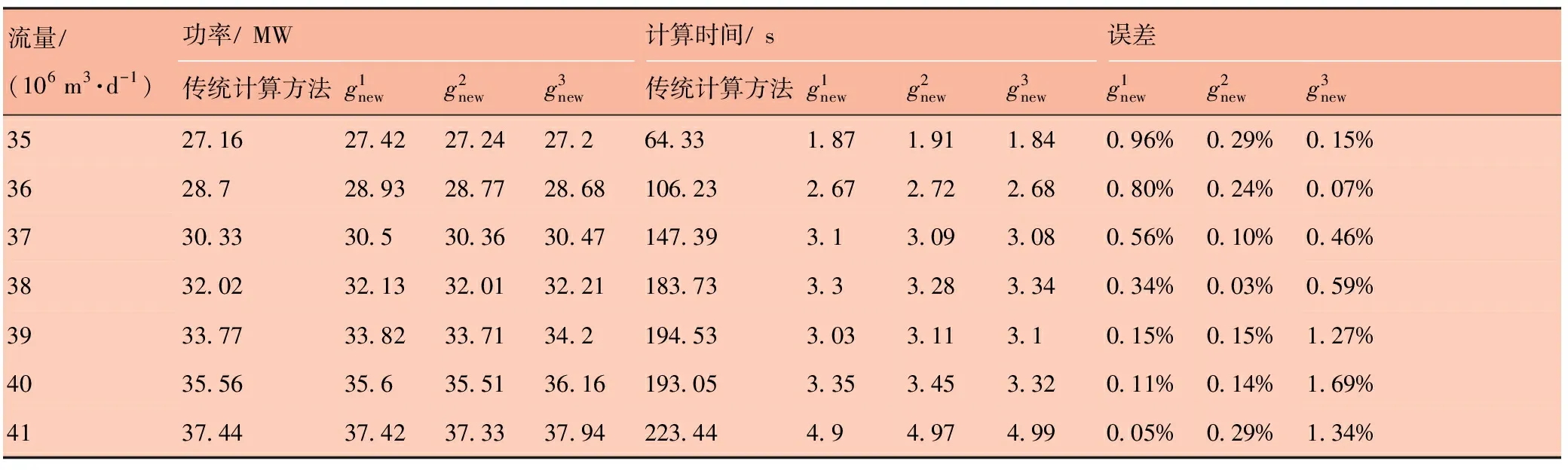
表6 案例分析实验结果表

4)与传统计算方法相比,使用3个新的拟合函数后的求解时间均减少了97%以上,求解效率大大提高。

5 结论