基于FLAC数值模拟的巧家县白泥沟滑坡稳定性分析

王 壮, 苏 雷，*, 时 伟, 张拥军, 凌贤长, 2

(1.青岛理工大学 土木工程学院，青岛 266525；2.哈尔滨工业大学 土木工程学院，哈尔滨 150090)

山体边坡常常发生各种破坏现象，其中滑坡是最常见的破坏形式。山体滑坡具有巨大的破坏力，其发生时携带大量岩土倾泻而下，对人们的生命与财产安全造成巨大的威胁。诱发山体滑坡的因素众多，如降雨、地震、人工开挖和工程爆破等，其中降雨、地震等自然现象是无法避免的，许多滑坡的产生也与此相关，如2008年汶川地震发生后，诱发了数以万计的滑坡灾害，造成巨大的人员伤亡及财产损失[1]；2006年的马达岭滑坡由连续降雨引发，该滑坡破坏了大量的农田及道路，所幸未造成人员伤亡[2]；2017年九寨沟发生MS7.0地震，触发大量的滑坡灾害，地震共造成25人死亡、6人失踪、525人受伤、1万多人受到影响，73 671间房屋受损，经济损失达80.43亿元[3]。

滑坡的分析方法主要有极限平衡法与数值分析法，其中数值分析法考虑土体间的应力-应变关系，可以在短时间内获得较多的体系反应量，因此众多研究人员采用数值模拟的方式对滑坡进行研究。如杨笑男等[4]介绍FLAC在特殊性岩土滑坡灾害治理评价中的一般方法，应用FLAC对典型黏土质硅藻土边坡的滑坡防治措施进行优化设计和数值模拟分析，提出经济合理的综合防治建议。张小雪等[5]采用颗粒流(PFC)模拟方法，对黏土试样的双轴试验进行数值模拟，并结合摩尔-库仑破坏准则，得到细观参数对宏观特性的影响规律，模拟黏性土坡在自重作用下变形破坏的全过程。王翔南等[6]克服扩展有限元法(XFEM)需要预先设定滑裂面的起始位置，以及滑裂面前端扩展方向的判断精度较低等缺陷，使扩展有限元法可以自动判断裂缝发生位置，提高其对滑坡破坏过程的模拟精度。王宵等[7]采用离散元软件UDEC4.0和有限差分软件FLAC3D，分别建立二维和三维数值模型模拟边坡破坏过程，结果表明岩石类边坡变形破坏主要经历三个时期，李守巨等[8]采用有限元强度折减方法评估含节理岩石边坡的稳定性，计算临界滑移面的安全系数，通过Drucker-Prager破坏准则判断岩石边坡有限元模型中每个单元的滑移状态，采用准静态方法模拟岩石边坡地震作用荷载，讨论地震动力放大系数对边坡抗滑稳定性安全系数的影响。

考虑到滑坡具有大变形的特点，FLAC计算程序采用显式差分法求解微分方程，在大变形问题的分析方面具有独特的优势[9]，因此本文采用FLAC计算程序模拟白泥沟滑坡，计算分析其在自重、降雨及地震工况下的稳定性。

1 工程地质概况及滑坡特征

白泥沟滑坡位于巧家县白鹤滩镇迆博社区跃进4组唐家山斜坡处，距离巧家县县城南侧5 km。白泥沟滑坡整体形态呈扇形，后缘清晰，两侧边界较为明显。滑坡体宽约350 m，长约300 m，滑坡面积约7.58×104m2。滑坡后缘、前缘标高高差117 m，滑坡体厚度最大为45 m，平均厚度32 m，滑坡体体积约2.5×106m3，属于巨型厚层基岩滑坡，滑坡区全貌如图1所示。

滑坡前缘存在采石场，开挖后造成卸荷作用导致滑坡后缘出现张拉性裂缝。滑坡区出露物质为残坡积土及灰岩，其中表层残坡积土由棕红色粉质黏土与碎石土组成，厚度分布不均。下覆基岩以灰岩为主，由钻孔岩芯可见，基岩具有强风化特征，岩体受构造挤压极其破碎，岩体透水性强。滑坡局部夹杂泥化软弱夹层，厚度为2～5 m，分布在地下25～40 m处，夹层倾角20～25°，接近山体斜坡倾角。钻探结果显示，钻孔深度内未见地下水，但由于雨水沿滑坡后缘裂缝入渗，导致泥岩层含水量较高，且该泥岩层具有良好的隔水效果，在雨水浸润下，抗剪强度明显降低。滑坡所在地区地震活动频繁，地震作用增大坡体的下滑力，从而促进滑体沿泥岩层产生滑动现象。

2 FLAC数值模型建立

2.1 模型的建立及参数选取

模型依据白泥沟滑坡地质勘察剖面图建立，模型长约389 m，模型坡顶至模型底部约215 m。模型上部覆盖粉质黏土，中间分布软弱夹层，地质勘察为黏土层，基岩为强风化灰岩，滑体由粉质黏土及强风化灰岩两部分组成。根据地质勘察报告[10]，各岩土层物理力学特性参数见表1，各层材料均采用摩尔-库仑屈服准则。网格划分考虑地震波在模型中传播的数值精度[10-12]，最大网格边长为1.6 m，x，y方向分别划分248，179个节点，共44 392个网格。静力计算下，模型两侧采用x向约束，模型底部采用x，y双向约束。FLAC数值模型如图2所示。

图1 白泥沟滑坡全貌[10]

图2 FLAC数值模型

在数值模拟中，FLAC采用强度折减法计算坡体安全系数。自重工况下的滑坡稳定性计算采用天然状态下的岩土物理力学特性参数；考虑到勘察报告中指出在钻探范围内未见地下水，所以本文未考虑孔隙水压力上升及岩土体内部渗流，在降雨工况下，将滑体材料参数改为饱和参数，用于计算坡体的稳定性；地震作用下的计算只考虑天然状态下的材料参数。

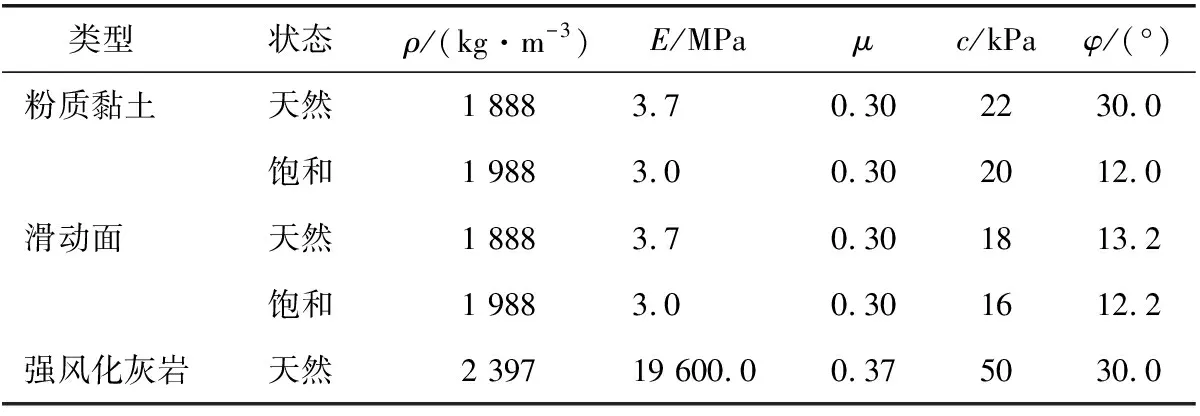
表1 白泥沟滑坡模型岩土物理力学特性参数

2.2 模型合理性验证

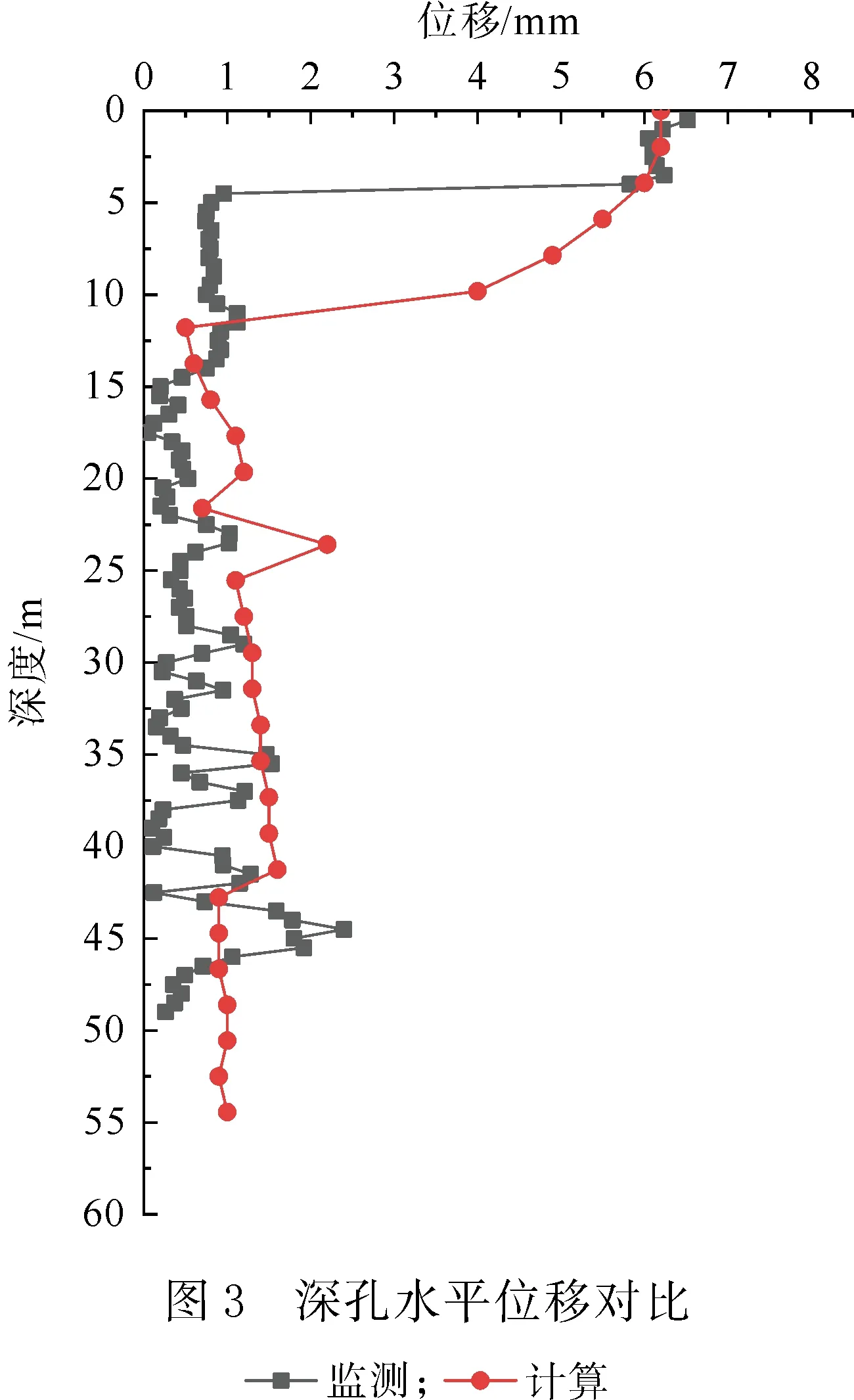
工程中为查明滑坡的分层、分级情况及滑面深度，掌握滑坡的变形速率及滑动方向，采用测斜仪对滑坡进行了深孔位移监测，记录坡体内部水平位移情况。依据实际工程中的深孔位置，在数值模型中记录相同位置的水平位移，并在自重作用下对模型进行计算。监测和计算的水平位移对比如图3所示。计算与监测的水平位移整体趋势一致，其中滑坡表面位移量一致，滑动面处(22～25 m)位移均出现增大现象，表明数值模型能够再现滑坡不同深度的位移。但是由于工程正处于施工中，受人工作业的影响，且监测位移量在毫米量级，致使数值模拟结果与监测结果存在一定的差异。

2.3 地震波处理

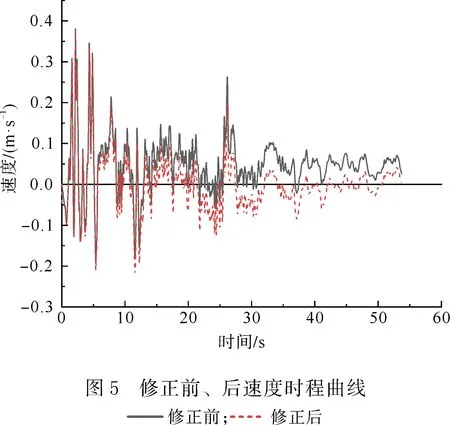
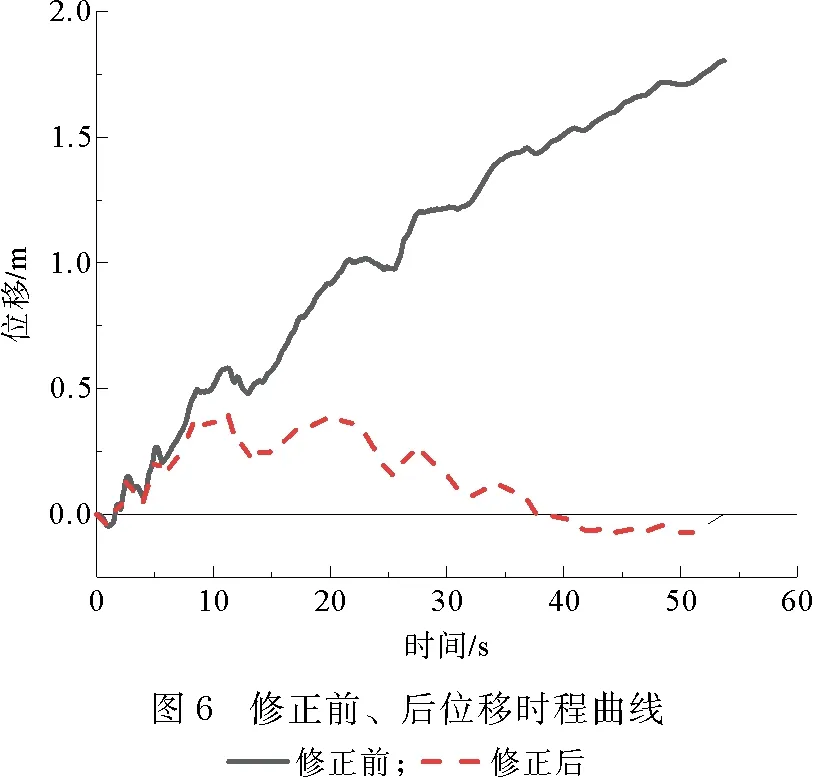
在数值模拟中，采用1940年Imperial Valley地震中的El Centro波，地震波如图4所示。地震波最大加速度0.349g，发生在2.12 s，地震波时间间隔0.02 s，总时长53.74 s。由地震波得到的最终速度与位移均不为0，如果直接将地震波施加到模型中进行计算，将导致FLAC模型在地震波结束后依旧存在持续速度或残余位移[9, 11-12]，因此需要将地震波进行基线修正处理。基线修正可以借助FLAC中的Fish语言功能实现，修正前、后的地震波速度、位移时程曲线如图5、图6所示。

2.4 地震波输入及阻尼的选取

地震波的施加方式有两种[9, 11]，第一种是直接在模型底部施加加速度或速度时程，该方式适用于刚性地基，即模型底部为模量较大的材料。第二种是将应力或力时程施加到模型中，该方式需要在模型底部施加静态边界。第一种方式存在潜在的缺点[11]，即模型底部的运动是完全指定的，相当于在底部施加了一个位移边界，对于一般模拟计算是不适用的。本文采用第二种方式实现模型在地震工况下的模拟计算，应力时程可以由速度时程通过公式σn=factor(ρCp)vn计算得到。式中：σn为应力；ρ为模型底部材料的密度；Cp为纵波在模型底部材料中的传播速度；vn为速度；factor需要进行试算，将得到的应力时程输入到模型中，并记录模型底部的速度响应时程，与速度时程进行对比，得到最合适的factor值。经过试算，本文中factor值为1.0。模型底部施加x和y向静态边界，使用静态边界可以较好地吸收地震反射波能量，防止地震波的反射；模型两侧施加自由场边界[9, 11]。

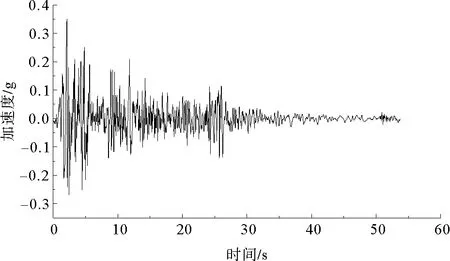
图4 地震波加速度时程曲线

地震工况下的模拟计算还需要设置合适的阻尼，FLAC提供三种阻尼类型，分别为瑞利阻尼、局部阻尼和滞后阻尼。相较另两种阻尼，瑞利阻尼可以近似地反映岩土体具有的频率无关性[10]，因此本次计算选用瑞利阻尼求解[13-14]，设置阻尼比为0.5%，中心频率为1.8 Hz。

3 数值计算结果分析

3.1 自重及降雨工况下结果分析

3.1.1 水平位移

FLAC采用强度折减法计算边坡安全系数，计算得到的自重及降雨条件下的安全系数分别为1.35，1.00，滑坡从稳定状态转变为欠稳定状态，说明降雨对滑坡的稳定性产生了较大影响。图7为自重工况下的水平(即x向)位移云图。由图可知，在自重工况下，滑坡的水平方向最大位移为0.25 m，发生在滑体表面上部的黏土层，与该位置坡度较大有关；滑体其余位置位移量在0.05～0.15 m之间。图8为降雨工况下水平位移云图。由图可知，在降雨工况下，模型水平位移扩大到了0.45 m，依旧发生在滑体表面上部的黏土层；滑体表面下半部黏土层的部分区域位移量有所扩大，达到了0.2 m；降雨主要影响了滑体表面黏土层的位移。

3.1.2 剪应力

图9、图10为自重及降雨工况下的剪应力云图。从图中可以得出，自重与降雨工况下的剪应力云图非常类似，均在滑动面中部产生应力增大现象，最大达到了2.5×105Pa，大于滑动面其他部位的5×104Pa。此处的应力分布也比较集中，这种集中现象容易造成局部剪切破坏，降低坡体的稳定性。可以说，该部位受到剪应力最大，且剪应力较为集中，容易产生滑动现象。

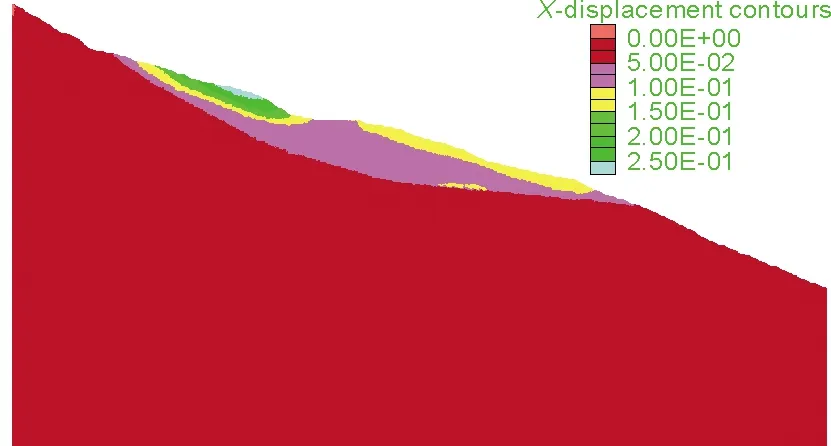
图7 自重工况下水平位移云图(单位：m)

图8 降雨工况下水平位移云图(单位：m)

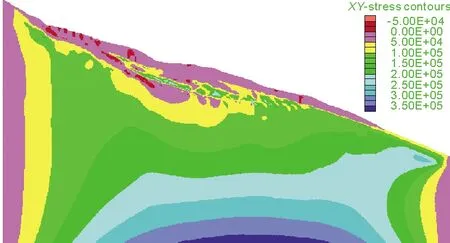
图9 自重工况下剪应力云图(单位：Pa)

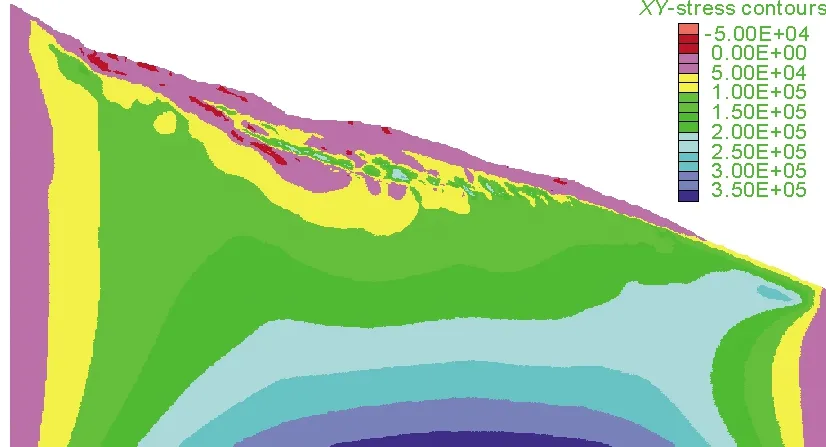
图10 降雨工况下剪应力云图(单位：Pa)

3.2 地震工况下的结果分析

3.2.1 加速度响应

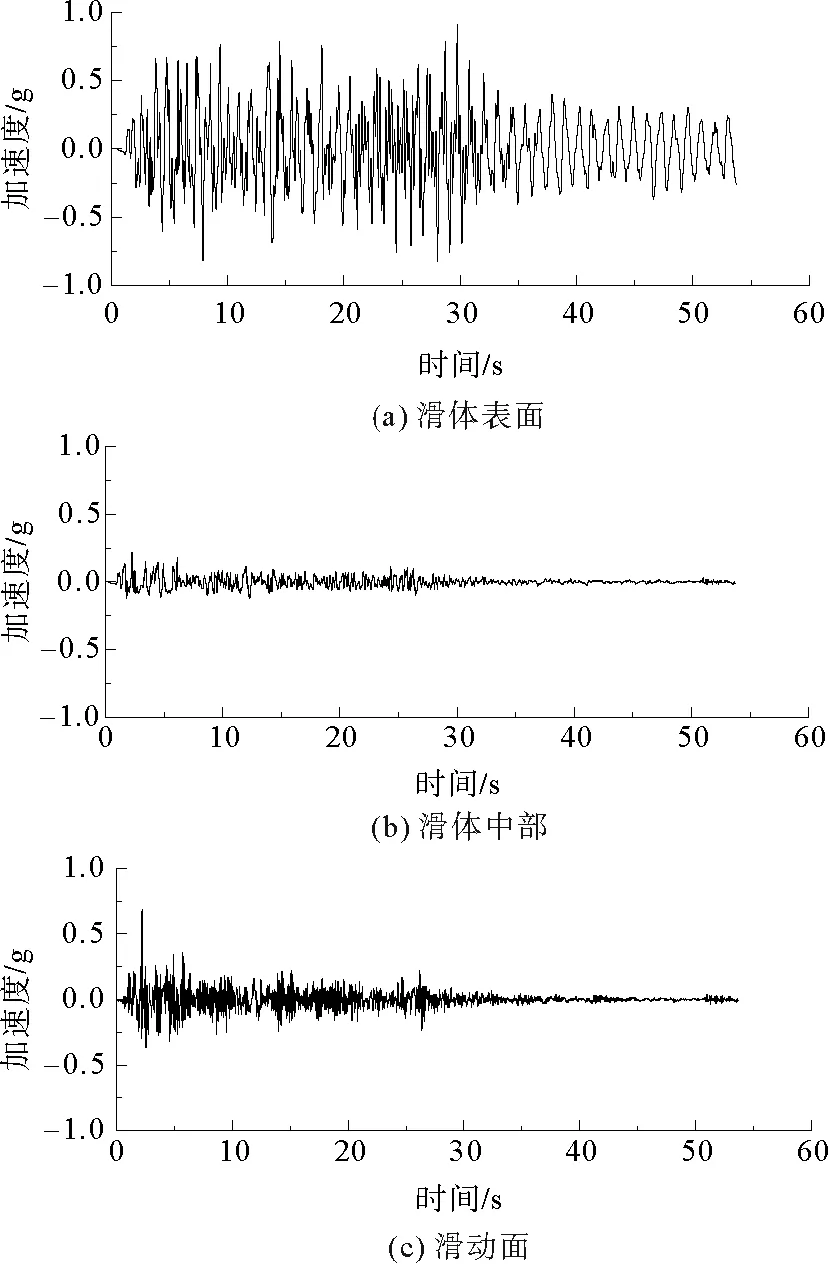
图11 监测点地震响应加速度时程曲线

在数值模型中，加速度监测点分别位于滑体表面、滑体中部及滑动面(具体位置见图1)，三点坐标依次为(115，179)，(115，164)，(115，149)。将监测点的最大响应加速度与输入的最大加速度相比，得到该点的加速度放大系数。监测点的加速度时程曲线如图11所示。从图中可以看出，滑体表面的加速度幅值最大，表明该处受扰动程度最激烈。滑体表面、滑体中部和滑动面最大加速度分别为0.91g，0.22g和0.69g。同输入的加速度相比，最大值分别放大了2.87，0.64和1.97倍，滑体表面及滑动面最大加速度均出现放大效应，而滑体中部最大加速度却有所减小。结合位移时程曲线(图12)，滑体中部加速度虽然较小，但其位移量始终处于滑体表面及滑动面之间。

图12为三个监测点水平位移时程曲线。从图中可以看出，三点的位移趋势一致，随着地震作用的施加，位移量呈波动性上升，在20 s左右达到位移最大值，随后位移值逐渐波动减小。滑体表面的位移波动十分剧烈，这应该与滑体表面为粉质黏土有关。从位移量上看，滑体表面黏土层的位移量始终最大，其次是滑体中部，滑动面的位移量始终最小。由图12知，在地震结束时刻，位移随时间仍不断增加，呈现一定的增加趋势，说明滑坡在地震作用下发生了破坏[15]。

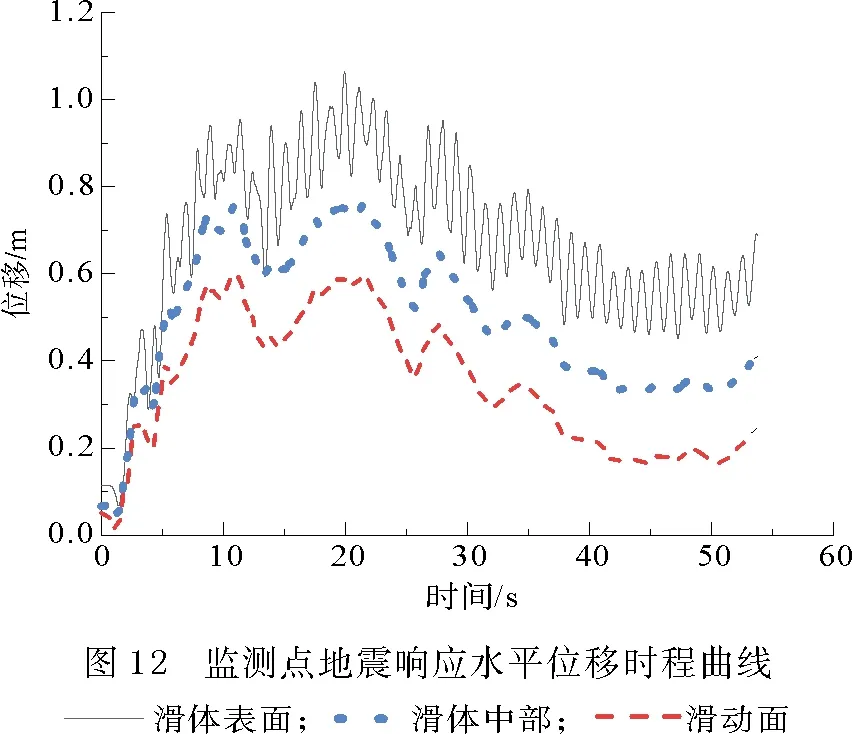
图13 地震结束后水平位移云图(单位：m)

3.2.2 水平位移响应

图13为地震结束后的水平位移云图。从图中可以看出，滑坡的最大位移达到了0.75 m，比自重工况下的位移增大了0.5 m，比降雨工况下增大了0.3 m，发生位置依旧在滑体表面上部的黏土层，滑体表面下半部的黏土层位移也达到了0.50～0.75 m，滑体其他位置水平位移处于0.20～0.50 m之间，与滑床之间存在相对位移。

3.2.3 剪应力、最大剪应变响应

图14、图15分别为地震结束后剪应力和最大剪应变增量云图。最大剪应变增量可反映岩土体的剪切变形程度，其分布范围及贯通情况可直观反映滑坡潜在破坏滑动面的分布位置和发展趋势[16]。从图14可以看出，地震工况下的模型未出现剪应力增大或应力集中现象。从图15中可以看出，最大剪应变增量最大值发生在滑动面中部，达到0.175，且最大剪应变增量在滑动面位置呈贯通现象，表明滑体容易产生滑动现象。

图14 地震结束后剪应力云图(单位：Pa)

图15 地震结束后最大剪应变增量云图

4 结论

1) 数值模拟表明：自重和降雨工况下安全系数分别为1.35和1.00，表明降雨降低了滑坡的稳定性。在这两种工况下，滑动面存在剪应力集中现象，容易导致局部产生剪切破坏。最大位移产生在滑体表面上部的黏土层，与自重工况相比，降雨使黏土层位移量明显增大。

2) 地震工况计算表明：地震作用下滑体不同部位动力响应差别明显。从位移上看，滑体表面水平位移量最大。从加速度动力响应上看，滑体表面、中部及滑动面加速度时程变化趋势一致，滑体表面加速度放大系数最大。模型并没有出现应力集中现象，但在模型滑动面处最大剪应变增量呈贯通现象，表明在地震工况下，滑体易产生滑动现象。

3) 综合自重、降雨及地震工况下的模拟情况，剪应力及最大剪应变增量最大值均发生在滑动面中部位置，对滑坡进行防治时，应注意该位置的位移、应力及应变情况。针对滑体上部黏土层位移量较大的情况，建议对其进行削坡处理。