基于改进Dijkstra算法的输电线路路径规划

张 超，李 欣，赵祥伟

(中国能源建设集团江苏省电力设计院有限公司，江苏 南京 211102)

0 引言

输电线路选线规划是电网规划设计的重要内容，传统的路径选线通常包括图上初选、搜资、初勘、设计方案、现场终勘、线路评定等工作[1]。由于前期的搜资和现场勘查需要花费大量的时间、人力和物力，而且搜集到的地理信息常常无法保证时效性和准确性。传统的选线方法跟专业人员的能力和经验密切相关，但线路设计考虑的因素和原则常常容易顾此失彼，无法得到最优的路径[2]。

随着地理信息技术的快速发展以及智能路径规划算法的涌现，输电线路智能路径规划逐渐得到业内人士的关注。余凤先[3]等应用地理信息系统(geographic information system，GIS)具有的定性、定量、定位分析功能进行九龙—石棉500 kV送电线路的优选工作，朱义中[4]等将层次分析法应用于地理信息系统输电线路决策支持系统中，实现线路路径的优选，陈小红[5]等引入元胞自动机模型，确定输电线路所要经过的各个元胞及走向，最终形成输电规划的路径，苏海峰[6-8]等介绍了改进蚁群算法和元胞自动机模型在输电线路路径自动选择中的应用。

Dijkstra算法是目前最短路径规划问题的基本算法，已广泛应用于公路、铁路、输电线路、油气管道等的路径规划中。本文采用专家决策法确定地图栅格综合成本，并通过限制目标搜索区域，减少无意义运算，提高Dijkstra算法搜索效率，能有效改善输电线路路径规划的效果。

1 Dijkstra算法

1.1 基本原理

Dijkstra算法是荷兰科学家狄克斯特拉于1959年提出的启发式搜索方法，故也叫狄克斯特拉算法。其基本思想是：从顶点V0出发，搜索从它到其他各顶点的最短路径。把有向图中的顶点集V分成两个子集S和T，S为已求出最短路径顶点的集合，T为尚未求出最短路径的顶点集合；循环遍历集合T，每次找出最短路径的顶点放入集合S中，直到集合T为空。

图1 Dijkstra算法示意图

如图1所示，设带权有向图G={V，E}，V=V0，V1，…Vn-1，用带权的邻接矩阵Arc表示 图G；Arc[i][j]表 示 弧 (Vi，Vj)上 的 权 值，S表示已求出以为起点的最短路径终点的集合；向量D的每个D[i]表示当前求得的从起点V0到每个顶点Vi的最短路径的长度，利用Dijkstra算法从源点s到终点t的步骤如图2所示。

图2 Dijkstra算法流程图

不同于图论和矢量GIS的传统线型网络最优路径搜索，基于栅格地形的最优路径搜索可以作为虚拟栅格网络的最优路径搜索，是一种格网邻域模型的路径搜索。根据栅格单元隐含的邻接关系，栅格数据模型可以通过连接相邻的节点来抽象成栅格网络。目前常用的格网邻域模型有四、八和十六格网邻域结构，其中八邻域模型不仅具有复杂度低，而且精确度高、时间性能好等优点，本文采用八邻域结构(如图3所示)。

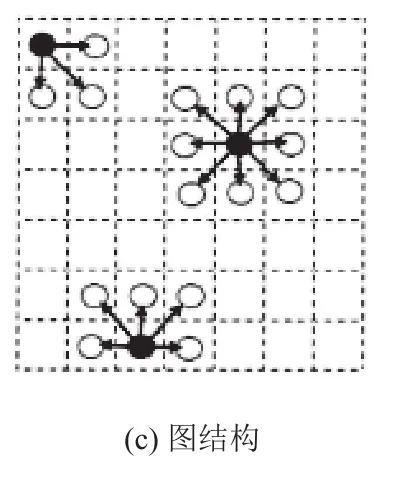
图3 八邻域模型结构图

八邻域模型实现Dijkstra算法的过程如图4所示。

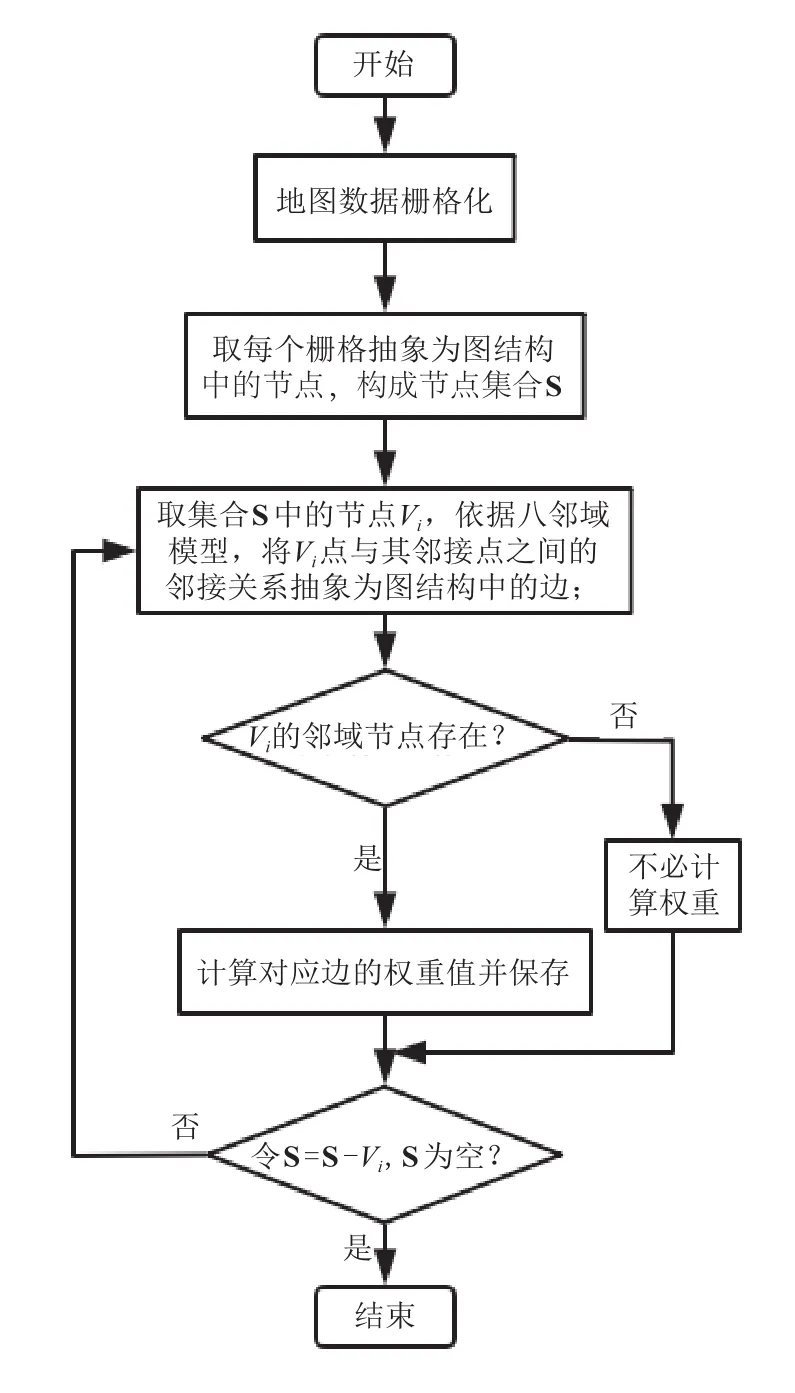
图4 Dijkstra八邻域模型算法流程图

1.2 算法改进

Dijkstra算法能够计算出两点之间最短路径的最优解，而且鲁棒性很强，但随着节点数量的增大，它的计算效率会降低。由1.1节可知，Dijkstra算法采用带权的邻接矩阵存储图形数据，占用大量内存空间；并且它是一种盲目或无向搜索算法，对于具有n个节点的图，它的算法时间复杂度为O(n2)，计算时间和存储开销都比较大。本文采用限制搜索区域[9]加载部分栅格模型，提高搜索效率，降低搜索时间。

Dijkstra算法的搜索过程类似于以起点为圆心不断向外扩展的一系列同心圆，是一种无向搜索，它没有考虑终点所在的位置或方向，因此在不断向外搜索的过程中，其他顶点与终点被搜索到的概率相同。当起点和终点距离较远时，会产生大量无意义的搜索，降低搜索效率，收敛时间大大增加。起点到终点之间除了距离关系外，还有方向的关系，两点之间的直线线段代表了最短路线的趋势方向，即最短路径顺着这个趋势方向的概率极大。因此，为了减少无意义的搜索，以起点和终点作为矩形区域对角线的两个顶点，只遍历矩形范围内的栅格。当发生矩形内的路径被障碍物阻挡而需绕至矩形外的情况时，本文采取的方案是逐步扩大矩形的范围，直到搜索到最优路径。

1.3 模拟实验

图5中红色圆圈代表障碍物，蓝色米字代表起点，红色米字代表终点。为了提高搜素效率，通过在周边设置障碍物的方式，阻止或减少无效的路径寻找。

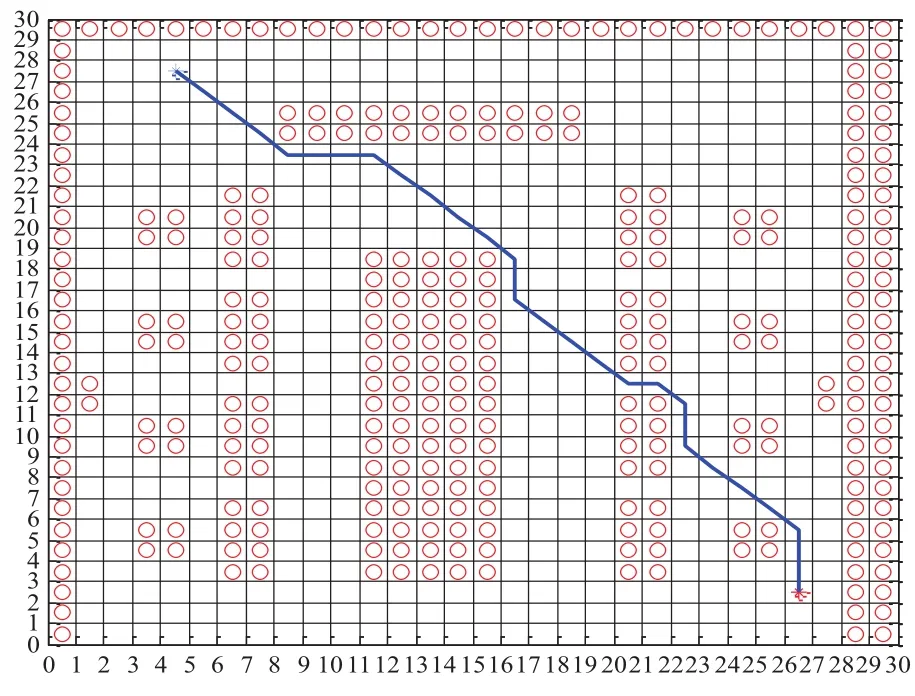
图5 模拟最短路径

2 输电线路智能选线Dijkstra算法建模

2.1 栅格数据准备

由于线路设计人员搜集到的资料通常都是遥感影像，而Dijkstra算法搜索最短路径是建立在栅格基础上的，所以需要对遥感影像进行栅格化处理。进行栅格化之前，需要对遥感影像进行地物分类，如房屋、道路、河流、农田、林地等，根据这些环境因素对输电线路选线的影响程度分别赋予不同的权重。

2.2 路径成本计算

Dijkstra算法采用“节点/联系”模型来表达，每个栅格被认为是一个节点，两个相邻节点用“联系”来连结，这个“联系”被表示为成本或代价。由于使用八邻域模型，故从某个节点出发会有8个方向，这8个方向又可分为两类，直线方向(上下左右)和斜线(对角)方向。每个栅格都被赋予相应的权重值，即线路经过此栅格的成本代价，用costi(i为栅格编号)表示。如图1中直线方向的“联系”值就是相邻两个栅格成本的平均值，如A、B两点间的联系成本为costAB=(costA+costB)/2，A、C两点间的联系成本为costAC=1.414×(costA+costC)/2，A、E两点间的累计联系成本为costAE=costAC+1.414×(costC+costE)/2。

从源点到终点，产生累计成本栅格数据以找到最佳路径，就是一个从源栅格开始向外探索的过程。如从源栅格A出发，首先搜寻相邻的东、西、南、北、东北、西北、东南、西南几个方向的8个栅格，用上面的公式计算相应的联结成本。由于这8个邻域栅格均可以到达源栅格，所以将他们放入OPEN列表中，然后对这8个栅格逐一扩展，将他们的邻域栅格加入OPEN列表，同时将这8个栅格加入CLOSE列表，代表已经遍历完毕。源栅格不一定要求是相连的，所有不相邻的栅格对于OPEN列表的贡献是相等的，只有具有最低成本的栅格才会被选择，其邻域栅格才可以被扩展，而无需考虑是从哪个源栅格开始计算的。逐渐向外扩展的过程中，如果发现某栅格有多个后向联结栅格，那么将具有最低联结成本的栅格安排到CLOSE列表中。计算累计成本时，这些成本也会计算新的被列入CLOSE列表中的栅格成本值，即使邻域栅格是从另外一个源栅格开始计算的。如果新的累计成本值比当前值大，则该值不计入；如果新累计值小，则当前位置栅格的累计成本会被新累计值代替，这表明根据新栅格发现了成本更低的一条路径，所以将其安排进CLOSE列表。如果扩展栅格有多个源栅格，扩展过程将继续将最低成本栅格加入到OPEN列表中，而不用顾及是从哪个栅格开始的，直到找到最终的最低成本也就是最优路径。

3 实例分析

3.1 实验数据来源及处理

本文采用的实例数据来源于江苏某220 kV线路工程，如图6所示，该线路地处江苏北部平原地带，地势平坦，地物以田地、房屋、道路、河道为主。因为输电线路跨越房屋会产生较大的拆迁赔偿费用，故线路设计原则上尽量不跨越房屋，道路上不允许立塔，河道尤其是通航河道立塔条件较差，一般情况下田地最适合立塔。基于上述分析及专业工作经验，本文对田地、房屋、林木、河流赋予的权重或成本值分别为1、4、3、2。

图6 实验区域的影像

首先对遥感影像进行矢量化，该过程也是一个地物分类的过程，本文将该区域的地物分为田地、房屋、林木、河流4类，如图7所示，其中浅绿色表示田地，粉色表示房屋，深绿色表示林木，蓝色表示河流。每种地物矢量化后，在属性表中添加权重值的属性。分类结束后，需进行栅格化，考虑到栅格边长太长，会导致分辨率低，地物抽象失真；栅格边长太短，会导致分辨率过高，栅格数量过多，搜索过程过长，因此栅格边长应取值适当，本文将栅格的边长为50 m。划分栅格以后，将每个栅格的权重属性赋予栅格中心，这样就完成了路径搜索前的数据准备工作。

图7 矢量化后的效果图

3.2 选线结果分析

设置起点和终点，并限制优先搜索区域，便可以进行最短路径寻找，结果如图8所示。可以看出，该路径避开了房屋和林木，而且距离较短，基本符合最优路径要求。

图8 最短路径栅格效果图

传统的Dijkstra算法耗时2.61 s，改进后的Dijkstra算法路径搜索效率耗时为1.82 s，相比传统算法提高了30%，效果显著。算法效率的提高程度与路径起终点在整幅图中的分布位置有关，当两个点在图的中间位置时，效率改善程度最高；在对角位置时，改善程度最低。

在很多情况下，运用智能路径规划算法得出的路径往往还需要进行适当的人工干预，因为在实际的输电线路工程中，要考虑的因素不止本文中所提到的几种，还包括地质、覆冰以及转角数量等很多其他因素。

4 结语

输电线路路径设计是一个复杂耗时的工作，结合地理信息技术能够大幅提高线路路径设计效率。本文使用地理信息技术，将遥感影像分类并栅格化，采用智能路径规划Dijkstra算法，并使用MATLAB编程实现，在输电线路设计工作中取得了不错的效果。进一步地以线路起点和终点作为矩形区域对角线的两个顶点，只遍历矩形范围内的栅格，减少无意义的耗时搜索，效率比传统算法提升30%，改善效果显著，能够在输电线路选线设计中发挥较大的作用。