智能车辆路径跟踪的模糊滑模横向控制

陶 捷， 郑思远， 黄昭烨， 黄子成， 郑燕萍

(南京林业大学汽车与交通工程学院，江苏 南京 210037)

路径跟踪控制系统在当前的相关研究领域中，是一个热门课题。当前，经典PID控制国内外最常用的是路径跟踪横向控制方法[1-2]、滑模变结构控制[3-4]、模糊控制[5-6]、模型预测控制[7-8]、最优控制[9-10]和自适应控制[11-12]。这些控制算法都各有优缺点，有的不需要精准的数学模型但是控制精度低，有的控制精度高但抗干扰能力弱，有的鲁班性强但系统易出现抖动。因此，以单一控制算法设计的横向控制器很难同时满足准确性、稳定性和实时性的要求。

本文以智能车辆路径跟踪横向控制为研究目标，结合模糊控制和滑模控制两种算法的优点，不但将滑模变结构控制的特征予以了充分地保留，而且响应速度快，实现相对来说也是比较简单的，同时也具备模糊控制不需要精确模型、鲁棒性和容错能力强的优势，为多种控制方法融合提供参考。

1 车辆动力学模型与预瞄模型的建立

1.1 车辆动力学模型的建立

智能车辆在路径跟踪横向控制的过程中主要涉及横向和横摆运动。本文将其简化成为单轨车辆模型，获得了相应的车辆模型，车辆二自由度模型如图1所示。

通过计算来获得车辆动力学方程的矩阵形式[13]为：

(1)

改写成车辆运动状态方程为：

(2)

(3)

(4)

1.2 预瞄模型的建立

预瞄距离的选取在预瞄跟踪中至关重要。预瞄距离在很大程度上受车速变化影响，随着车速的增减，预瞄距离也需要增减，两者大体上呈正相关变化。基于郭孔辉院士的预瞄理论，笔者构建出来了关于车辆的预瞄模型。式(5)为该距离的计算公式：

(5)

式中：DLmin、DLmax为智能车辆最小和最大预瞄距离；Vx为智能车辆当前车速；根据相关试验[14]数据选取DLmax为15.6 m，DLmin为4.5 m，Vxmax为16 m/s，Vxmin为7 m/s，a1为1.233，a2为-4.131。

2 设计模糊滑模控制器

2.1 模糊滑模控制器总体设计思路

车辆横向控制系统主要目的就是为了基于控制器，来对车辆的行驶加以控制，控制系统整体框架如图2所示。

图2 控制系统整体框架

2.2 方位偏差和横向偏差融合

在本研究中，方位偏差以及横向偏差处理在一个维度的方式使用极值方法，增加了加权系数处理横向和方位偏差，通过这一方式分配两者的比重，得到集成偏差表达式：

(6)

式中：η1，η2均为大于零的系数，且η1+η2=1，eL即为融合后的偏差。

2.3 滑模函数设计

考虑到将滑模和模糊控制相结合的优势，本文将滑模函数作为模糊控制的输入，只需控制过程使滑模函数降到零即可。根据集成偏差特性，选取集成偏差来建立控制系统所需的滑模函数s：

(7)

其变化率表达式为：

(8)

式中：c1为常数。

2.4 模糊控制器设计

S={NB NM NS ZO PS PM PB}

δf={NB NM NS ZO PS PM PB}

在此设定论域集 X、Y、Z，集合均设为[-1，1]，然后转化对应论域。在选取隶属度函数时，考虑到三角形隶属度函数具有很高的控制灵敏度和准确性，在论域的零点附近使用，以获得精确而敏感的控制效果；在远离零点的区域中，采用更平滑的Z型和S型隶属函数，使控制效果更加稳定。

在设计相应的模糊控制规则过程中，充分考虑到了驾驶经验和交通规则生成模糊控制规则。Mamdani模糊推理方法相当普遍[15]，通过选择重心的途径来进行反模糊化的操作，模糊控制器控制规则见表1。

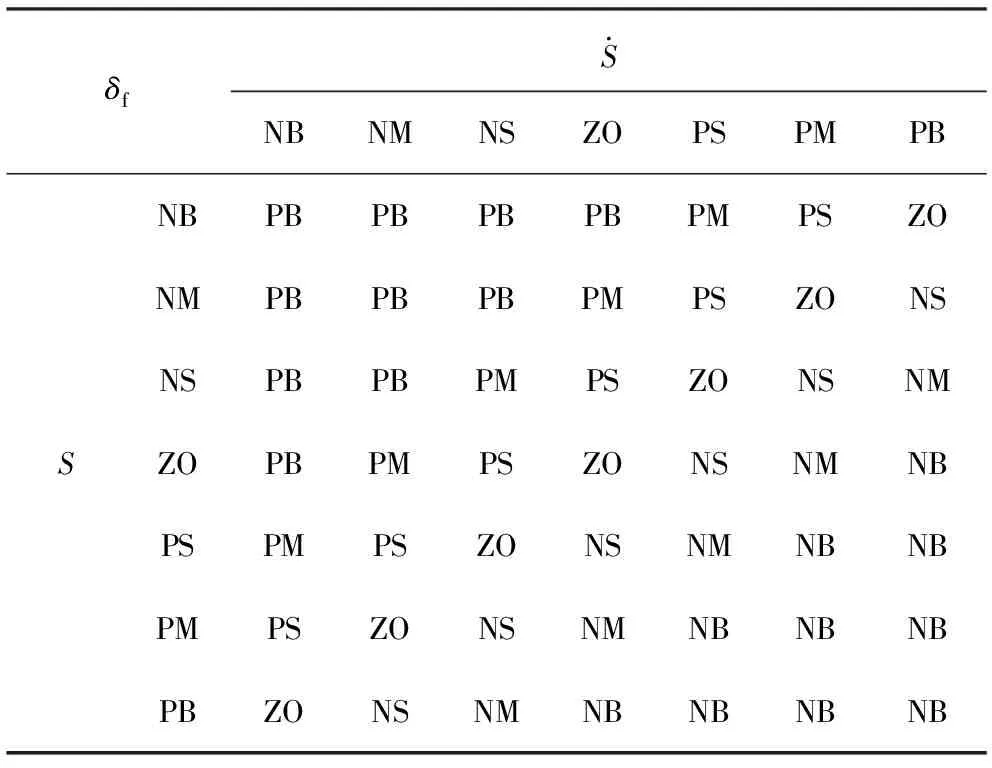
表1 模糊控制器控制规则

3 系统仿真及分析

3.1 控制系统仿真模型建立

本文仿真车辆模型的具体参数见表2[16]。

表2 车辆基本参数

在Matlab/Simulink中搭建了车辆动力学模块、道路曲率模块、预瞄模块、预瞄距离模块和模糊滑模控制器模块，完成了控制系统仿真模型的建立。

3.2 工况Ⅰ仿真分析

为了更好地反映出控制器在实际路径中的控制效果，工况Ⅰ选择了如图3所示的一段实际路径。数据来源：Open Street Map(OSM)众源地理信息数据平台。

图3 区域路径图

从目标路径中选取多个点位坐标，通过拟合速度快、精度高的最小二乘法拟合目标路径，在Simulink中以6次多项式得到拟合曲线：

y=f(x)=1.089 7×10-16x6-9.328 6×10-13x5

+2.957 9×10-9x4-4.215 7×10-6x3

+0.002 558 5x2-0.354 94x+2 284.9

where×∈[140,2 730]

拟合后目标路径如图4所示。

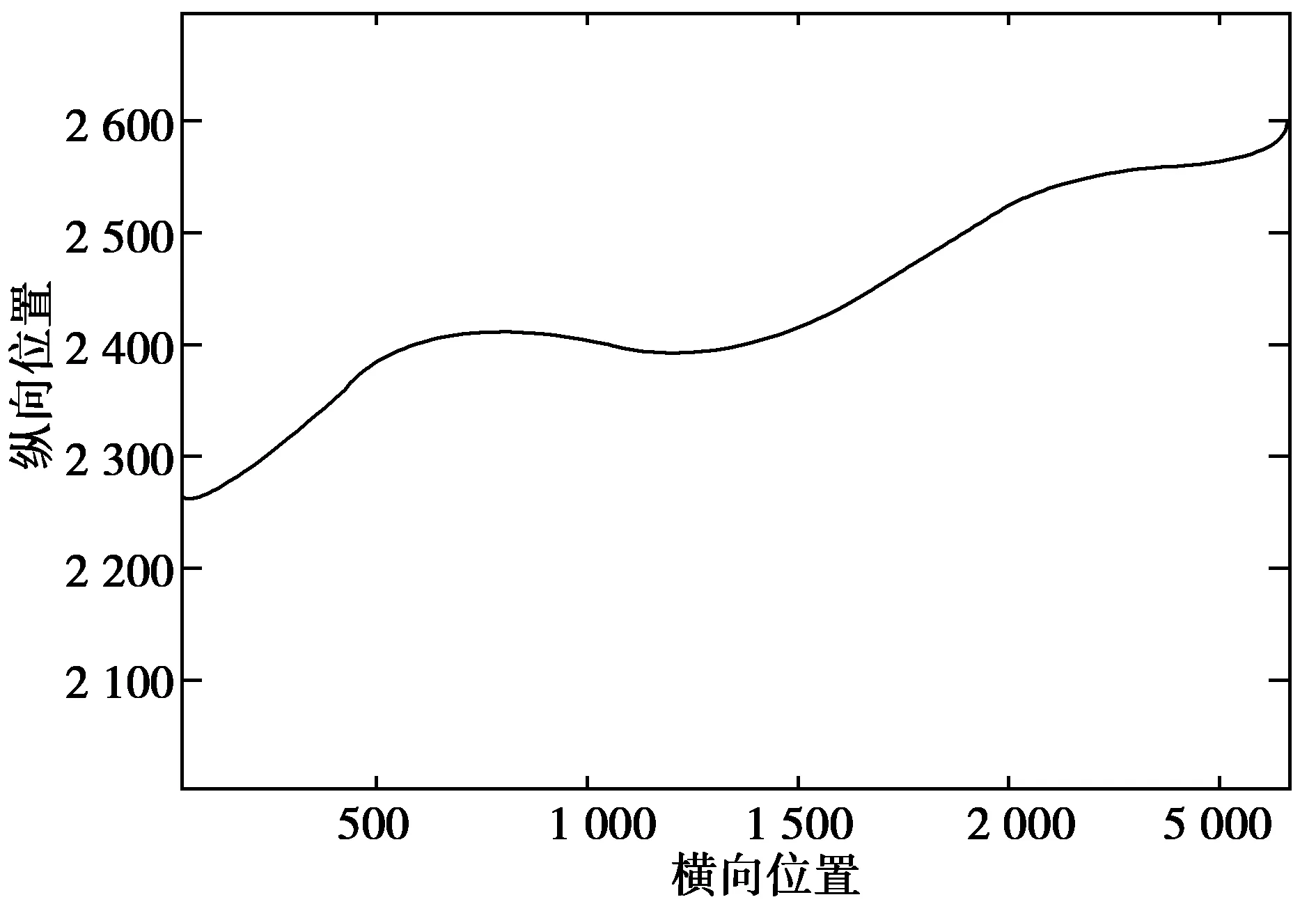
图4 拟合后目标路径

考虑到城市内行驶车速不会太高，故设置车速10 m/s。通过拟合曲线和曲率公式计算出道路曲率，并将目标路径曲率输入曲率生成器模块进行整体系统仿真，仿真时间共为240 s，初速10 m/s，预瞄距离为8.2 m，初始方位偏差0.1 rad，初始横向偏差0.2 m，得到前轮转角响应曲线如图5所示。

图5 前轮转角响应曲线

通过对前轮转角响应仿真曲线的分析可以看出，在一定的车速下，前轮转角输出曲线变化非常平稳，没有出现抖振，保证了自动驾驶汽车行驶过程中的稳定性，同时方位偏差稳定在±0.000 55 rad左右，横向偏差稳定在±0.02 m左右。结果充分说明了，所构想出来的控制方法能够以一种稳定、精确的状态跟踪实际路径。

3.3 工况Ⅱ仿真分析

工况Ⅱ选用生活中常遇到的侧方位泊车路径，经过一系列简化处理，具体轨迹与路径曲率如图6、图7所示[17-19]。

图6 运动轨迹

图7 路径曲率

同样，将目标路径曲率输入曲率生成器模块进行整体系统仿真，模拟时间需要设置为10 s，初始方向需要设置为0.1 rad，初始横向偏差需要设置为0.2 m，车速为-1 m/s，仿真结果前轮转角响应曲线如图8所示。

图8 前轮转角响应曲线

由图8可知，在大曲率工况下，曲线平滑无振荡，控制器稳定性好。但缺点是，前轮转角响应速度稍慢，方位偏差范围控制在±0.07 rad左右，横向偏差控制范围在±0.22 m左右，可见控制效果良好，能够满足实际泊车的需求。

4 结论

(1)本文将模糊、滑模两种控制算法的优势相结合，设计出智能车辆路径跟踪横向控制器。不仅发挥了滑模切换函数趋近速率快的优势，也保留了模糊控制鲁棒性和容错能力强的特点，并且采用方位偏差与横向偏差融合的集成偏差，降低了模糊控制的维数，减小了计算量，保证控制器的实时性和稳定性。

(2)应用Matlab/Simulink软件构建了车辆路径智能横向控制的仿真模型，在实际路径与侧方位自动泊车两种工况下进行仿真，测试控制器性能，其结果反映出了较好的控制效果，可以保证控制的精度，能够符合轨道跟踪和停车的需要。