基于复杂网络蜂群无人机网络拓扑结构分析*

林冰轩，徐明兴，陈志刚，沈雁鸣，甘文彪

（1.中国空气动力研究与发展中心，四川 绵阳 621000；2.北京航空航天大学无人系统研究院，北京 100000）

0 引言

蜂群无人机作战是未来无人机作战体系发展主要趋势，蜂群无人机之间通过相互协作和优势互补，能够大幅提升执行任务的成功率和生存率。蜂群无人机协同作战作为信息化时代的新型集群作战样式，具有显著的复杂网络特性。传统的分层级编队方法已经不适合当前复杂信息环境下蜂群无人机网络化运用的需要，借助复杂系统和复杂网络理论实现蜂群无人机网络化运行有望带来新突破。通过复杂性理论研究蜂群无人机运用，近年来得到了越来越多军事理论专家的认同。美国空军“2030 年科学技术发展战略”中，明确提出“在未来的冲突中要掌握时间、空间和复杂性的主动权”，并将之视为夺取未来空天优势的关键。

目前关于蜂群无人机网络化运用的概念已达成共识，但蜂群网络拓扑结构方面的研究还较少，而且其中大部分都集中在网络实例的实证研究，对基于复杂网络拓扑结构的蜂群无人机运用研究就少之更少了。如何进行分析、设计、改进蜂群无人机编队网络，使其实现信息的倍增效果，已经成为无人机集群智能相关的新兴研究领域。本文在传统树型编队网络研究的基础上，将蜂群无人机看作复杂自适应系统，基于复杂网络构造蜂群无人机网络拓扑结构，对网络拓扑结构的典型统计特性参数和抗毁伤特性进行分析，科学评估了基于复杂网络拓扑结构的蜂群无人机编队效果。

1 网络拓扑结构模型构造

本文分别构建了分层级的传统树形无人机编队和基于复杂网络拓扑结构的蜂群无人机编队。研究中不对各类节点的差异进行区分，采用无向无权图表示网络关系，将无人机个体视为网络节点，无人机之间的通讯视为边，任意两个无人机之间只要有信息交互，则两个无人机节点之间有连线，构建出二维网络图为无人机编队的网络拓扑模型。

网络拓扑模型研究中，采用矩阵来表示网络：设N 为全部节点的总数，则模型可以用N×N 的矩阵A 来描述，矩阵元A的值定义为节点v和节点v有无连接，有为1，无为0，研究中不涉及自环，因此，对角线的值为0。其一般表达形式如下所示：

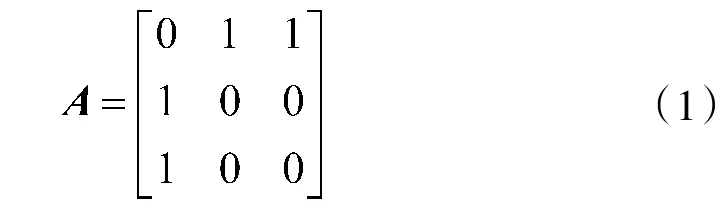
节点v的度k定义为与该网络节点形成连接的边数，度越大则节点在网络中越“重要”。网络中所有节点v的度k的平均值称为网络的平均度，记为＜k＞，即

网络中任意两个节点v和v的距离d代表从节点v和节点v的所有路径中最短的路径包含的边数量，它的倒数1/d称为节点v和v之间的效率。在无向网络中，平均路径长度L 则是任意两个节点之间距离的均值：

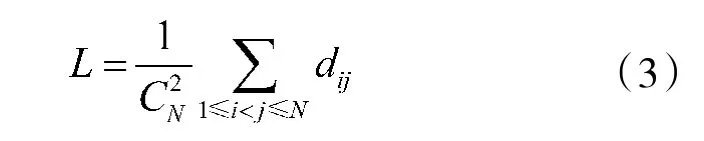
现实中复杂网络的平均路长通常较小，形成复杂网络的小世界现象，即任意两个貌似没有联系的节点，能够用较短的连接把它们联系在一起。

整个网络的聚集系数C 是全部节点聚集系数的均值。复杂网络是由不同粒度上关联密切的集群构成，集群内部关联密切，但多个集群之间只存在少量连接。与随机网络相比，复杂网络的集聚系数较高，通常在0.1～0.8 之间。

2 网络拓扑模型分析

2.1 传统树形网络拓扑模型无人机编队

传统无人机多机编队通常采用树形网络结构，由一个或多个簇群与指控中心构成网络，是以“指控中心”为中心的有中心网络结构，作为“中心节点”的无人机是实现簇群与指控中心构建信息交换网络的关键节点。各无人机单体之间信息传递较少，基本遵循“指挥中心-中心节点-子级节点-终端节点”的节点构造原则，自上而下地传递信息。因此，研究中采用树型网络来模拟传统无人机多机编队。“指控中心”即为树形网络的根节点（最高层节点），所在层次为0，指挥中心下面的“中心节点”无人机的层次是1，“子级节点”无人机的层级为2，“终端节点”无人机的层级为3，构造一个4 层的无人机多机编队网络，无人机总数量为85 架，具体节点和边如表1 所示。

表1 无人机树形编队网络数据

生成传统树形网络网络拓扑模型如图1 所示。每个终端节点的地位是对等的，而对于需要与“指控中心”进行信息交换的“中心节点”和“子级节点”，则是子网络的铰链节点。

图1 无人机树形编队网络拓扑模型

2.2 基于复杂网络拓扑结构的蜂群无人机编队

信息时代的蜂群无人机编队具有复杂网络的数学结构，该结构的基础是一个由链路连接的节点的集合。蜂群无人机复杂网络有着与规则网络和随机网络都不相同的拓扑统计性质，如“小世界特性”、“无标度特性”等，在节点和链路上的具体体现为：

1）节点特性。蜂群无人机采用分布式控制方式，网络中没有预设的中心控制节点。蜂群无人机节点的地位是对等的，无主从之分，能够根据无人机在蜂群网络中所处位置，在边缘节点和中心节点之间进行相应的角色切换。

2）链路特性。在蜂群无人机无线自组织网络中，通过无线资源使用、路由发现等控制方法，实现无人机节点之间的无线链路通信。无线链路受到有效通信距离的限制，当两个无人机之间的距离在某一特定值内，认为二者具有有效链路，超出这一距离，则认为二者无法通信。

基于蜂群无人机网络发展规律，提出了如下构建模型的思想：

1）设置M×M 的二维平面网格作为蜂群无人机分布区域，相邻两个网格点之间距离1，代表蜂群无人机之间的最小安全距离。

2）蜂群无人机总数量N 架，则设节点总数为N，在0～M×M 之间随机取N 个整数，对每个整数除以M 取商作为横坐标（x），取余数作为纵坐标（y），构成在二维平面网格上随机分布的节点v。

3）对任意两个无人机v和v在二维平面网格中的间距D进行计算，并与通讯距离D进行对比，如D≤D，则认为无人机v和v之间能够有效通讯，节点v和v之间存在边。

根据上述建模思想，借助MATLAB 生成N×N阶矩阵，即如果节点v和节点v之间有边，则矩阵元素A为1，否则为0，该矩阵即为蜂群无人机网络的连接矩阵，建立网络拓扑模型如图2 所示。

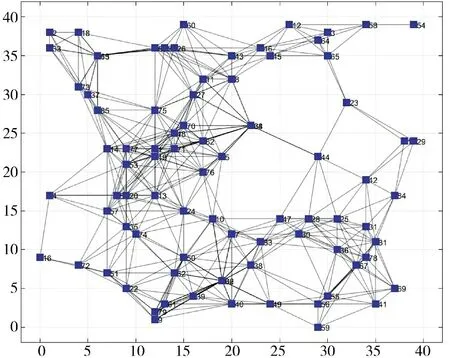
图2 蜂群无人机复杂网络拓扑模型

2.3 无人机网络拓扑模型性质分析

根据复杂网络参量计算方法，进行网络拓扑模型的平均路径长度、聚类系数、节点度等相关参数的计算。其中，进行复杂网络编队时采用了二维网格随机取点的方式，具有一定的随机性，本文进行了收敛性验证，图3 展示了蜂群无人机采用复杂网络编队的聚集系数和平均路长与随机取点运行次数的变化规律，结果表明，随机取点运行次数在20次以内变化波动较大，40 次之后基本稳定，为了确保数据可靠性，所计算复杂网络的聚集系数和平均路长均为50 次随机取点的平均值。

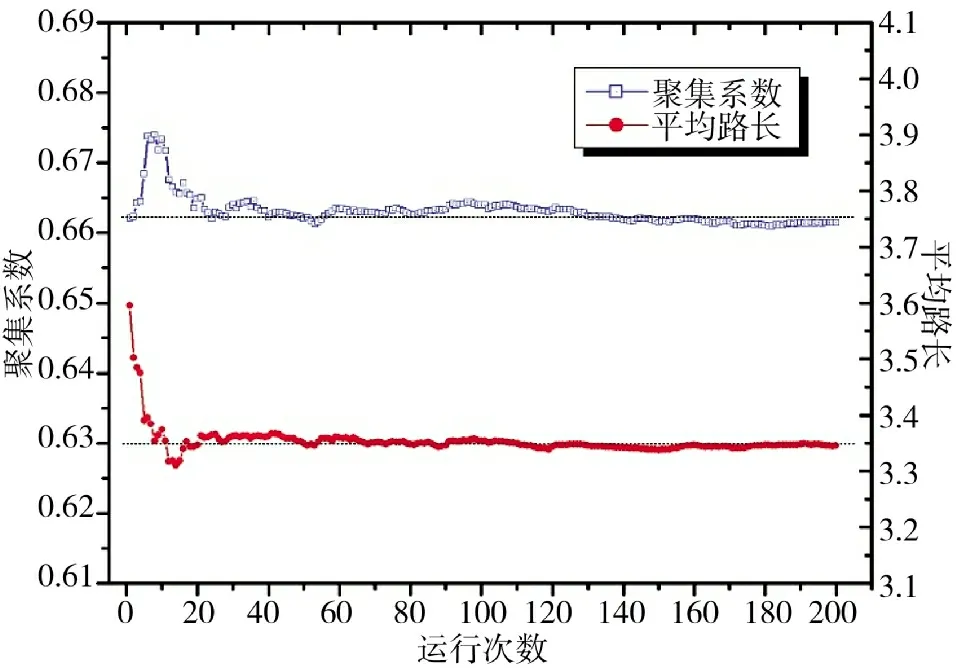
图3 聚集系数、平均路长与随机取点运行次数变化

经计算，得到传统无人机树形编队网络模型和蜂群无人机复杂网络模型的平均路径长度、聚类系数以及平均度值如表2 所示。

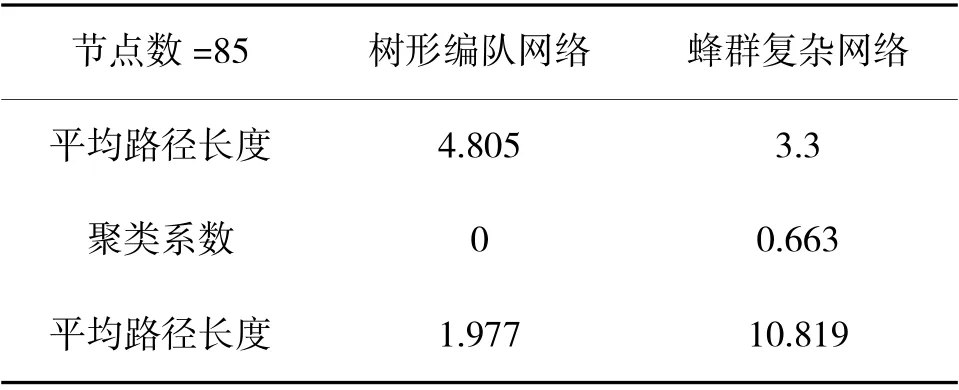
表2 两种无人机编队的网络模型统计参数对比

2.3.1 节点度

从树形编队网络图中可以清楚看到，大多数终端节点的度为1，只有少数“指控中心”、“中心节点”度为4 或5，该情况贴近真实的分层级无人机编队模式。节点度为1 的节点相当于无人机编队的末端执行单元，该类型无人机负责将收集的信息向上级节点汇报以及执行上级节点发布的任务指令，而这类末端无人机之间无法进行信息共享传输。度高的无人机节点属于上级指控节点，这类无人机虽然数量不多但负责的工作比较重要，与其通讯的无人机较多，成为无人机编队中的关键节点。担任指控节点的无人机汇集了整个无人机编队网络中的大多数信息，一旦被摧毁整个无人机编队将陷入瘫痪。基于复杂网络拓扑结构的蜂群无人机平均度为10.819，相比于传统树形编队，其网络拓扑模型具有较高的平均度值。在蜂群无人机复杂网络中，各无人机节点单元均处于连通的网络中，边缘节点和中心节点的角色可自由切换，实现蜂群无人机各单元间的组织协同。

2.3.2 平均路径长度

树形编队网络平均路径长度为4.805，蜂群无人机复杂网络平均路径长度为3.363，明显降低。在无人机编队网络中，任意两个网络节点之间的距离代表两架无人机信息传输所需要的跳数，蜂群无人机复杂网络的层次较少，网络中信息传输、共享和同步加快，有利于整个网络的信息交互。这也正是蜂群无人机涌现性的优势所在，多个无人机之间快速进行信息共享，不断进行交互后，以自组织方式产生远远超出个体效益之和的整体性质，使蜂群无人机实现1+1＞2 的突破。

2.3.3 聚类系数

计算结果表明，树形编队网络的聚类系数为0，说明传统的树形无人机编队按层级传递信息，网络内部松散，层级内无法互联互通，网络非常脆弱，编队受到打击后网络重建能力较差。而蜂群无人机复杂网络的聚类系数为0.663，各无人机节点连接紧密，即使在遭受敌方打击时失去了部分无人机单元，蜂群网络也能够借助其余无人机单元与重要节点建立通讯，进行网络重建。较短的平均路长和较大的聚集系数，表明基于复杂网络结构的蜂群无人机具有小世界特性，各无人机单元之间联系紧密，信息资源传递快捷。

2.4 无人机网络拓扑模型抗毁性分析

网络拓扑结构的抗毁性被定义为网络中节点或边遭受打击时，网络维持及恢复其联通的能力。不同拓扑结构的网络具有不同的抗毁性，复杂网络的容错抗毁性对于无人机编队研究是一项非常有意义的工作。

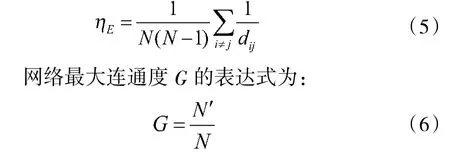
网络效率和网络最大连通度是衡量网络抗毁性的重要指标。网络效率η可表示为：式中，N'为无人机编队遭受攻击后网络最大连通集团的节点数。η和G 越大，网络重建能力越强。

计算得到无人机树形编队网络和蜂群无人机复杂网络在遭受敌方随机攻击时网络效率和最大连通度随被摧毁无人机节点个数的变化曲线，如图4、图5 所示。图中可见，蜂群无人机复杂网络的初始网络效率远高于树形编队网络。随着被摧毁无人机节点个数增加，树形编队网络的网络效率和最大连通度快速下降，当被摧毁节点达到一定数量时，甚至出现“断崖式”下跌。相比之下，蜂群无人机复杂网络展现出良好的抗毁伤特性，在部分节点被毁时仍然能够保持较强的重建能力。

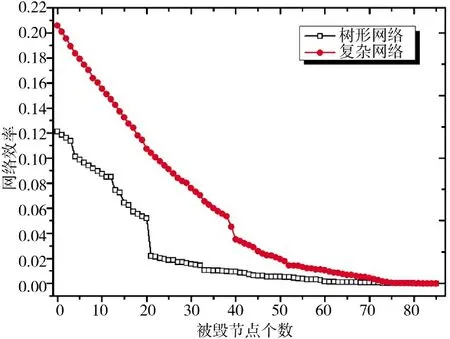
图4 网络遭受攻击后网络效率变化曲线

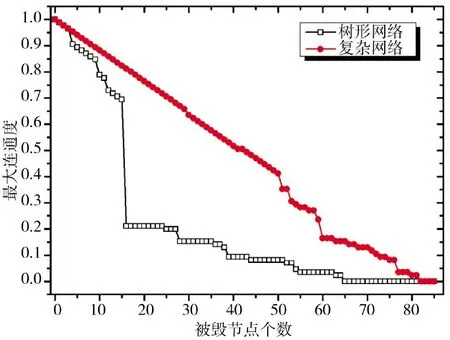
图5 网络遭受攻击后网络最大联通度变化曲线

为了对网络抗毁伤特性进行深入研究，采用基于节点收缩法的节点重要性分析。通过节点重要度评估分析重要的核心节点，是一种确定性网络分析方法，从网络拓扑结构出发研究抗毁性。

节点收缩法：这种方法假设在节点正常工作的情况下，将待测节点和与其相连的所有节点收缩为一个节点，对比不同节点收缩后得到的网络凝聚度来衡量节点的重要性。例如：节点V收缩是指将与节点V相连接的K个节点都与节点V短接，即节点V与周围的K个节点“凝聚成了一个节点”。若节点V是“核心节点”，则收缩后整个网络将更好地凝聚在一起。也就是说，收缩后网络凝聚度越大，该节点也就越重要。

根据收缩法，计算得到树形编队网络和基于复杂网络蜂群无人机的各个节点重要性计算结果，分别如图6 和图7 所示。从图6 中可以看出，编号为1的“指挥中心”重要性最高，达到了0.314，排序靠前的“中心节点”无人机和“子级节点”无人机的节点重要性分别为0.177 和0.064，而处于“终端节点”无人机的重要性仅为0.013，可见传统树形编队无人机网络非常脆弱，最高级的“指挥中心”节点被攻击，或者部分“中心节点”无人机被攻击，网络就会陷入瘫痪，从而造成网络效率和最大连通度的“断崖式”下跌。

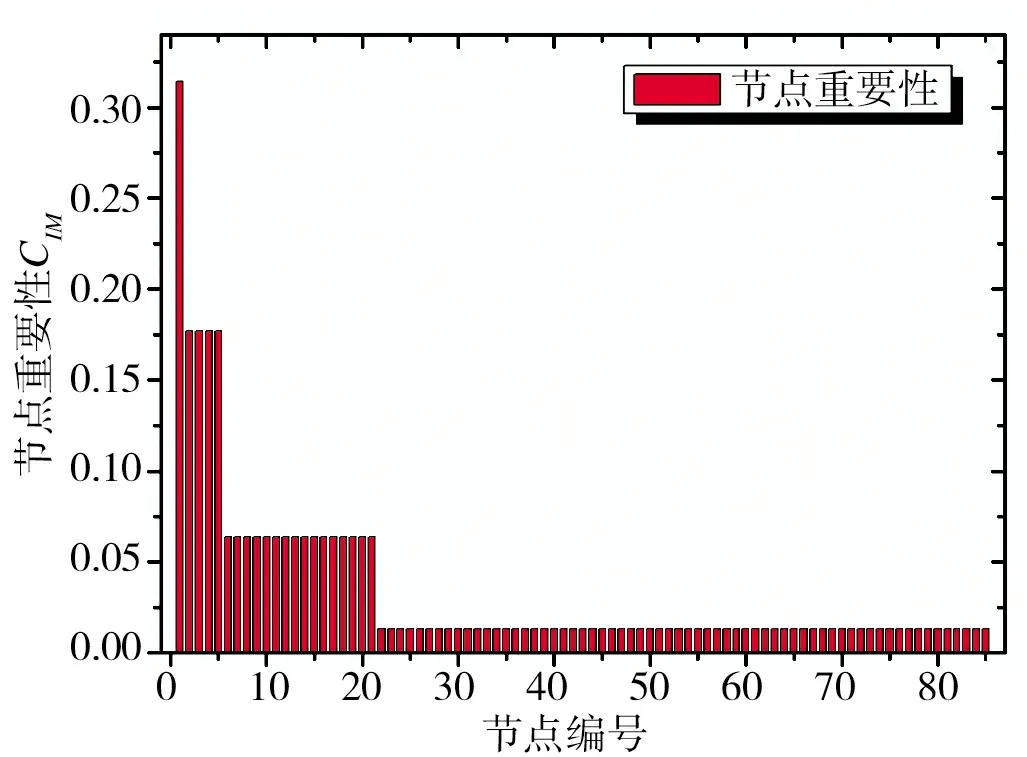
图6 基于节点收缩法的树形编队网络节点重要性分布图

图7 基于节点收缩法的蜂群复杂网络节点重要性分布图

对于蜂群无人机复杂网络的节点重要性计算结果表明，基于复杂网络拓扑结构的蜂群无人机节点重要性分布相对均衡，大多数无人机节点重要性在0.17 左右，没有出现重要性特别突出的中心节点，这意味着蜂群网络受到攻击时，被摧毁的节点为重要性相对均衡的一般节点，蜂群无人机网络模型中各节点仍具有较好的紧密性，保持足够的联通性维持其重建作战能力。

3 结论

蜂群无人机作战是未来军用无人机作战体系发展的主要趋势，基于复杂性理论设计了蜂群无人机复杂网络结构，并与常规树形树形网络的无人机编队进行了对比，分析了两种网络拓扑模型的统计特性参数和抗毁伤特性。结果表明，基于传统树形网络的无人机编队较为脆弱，网络内部松散，少量指挥节点在通讯中起到关键作用，受到打击后网络重建能力较差；基于复杂网络拓扑结构的蜂群无人机具有网络层次少，信息传输、共享和同步性强的优势，各无人机节点之间以自组织方式产生远远超出个体效益之和的整体性质。蜂群无人机复杂网络具有更好的抗毁性，受到破坏的蜂群复杂网络可通过其他无人机节点与重要节点取得联系，从而有效实现网络重建，极大地增强未来空战对抗体系的弹性。下一步工作重点是构建一套准确、量化的蜂群无人机协同效果评价指标和协同效果评价方法，分析、设计、改进未来蜂群无人机作战网络提供帮助。