数学黑洞495的Python求解和验证

丁大为 王德贵

通过前期的文章，我们了解了“数学黑洞6174”，也确实感到了数学中的玄妙。卡普雷卡尔（Kaprekar）黑洞，又称重排求差黑洞，其计算过程称为卡普雷卡尔运算，这个现象称归敛，“6174”称归敛结果。四位数的黑洞是“6174”，那三位数有同样的黑洞吗？

今天我们用Python来求解和验证。

数学黑洞问题，经过几天的研究，真的感觉很有意思，那么除了四位数的6174，三位数、五位数是不是也有类似的规律呢，这期分享三位数的黑洞。

找到三位数的数学黑洞是一个求解和验证的问题，也要解决以下三个问题。

一是输入任意一个三位数（不包含全部相同的数字），验证最后经过运算是不是得到一个固定的值;二是在一定范围内，是不是所有数都能得到这个固定值;三是要得到这个值最多需要多少步骤。

思路与四位数验证一样，首先要将三位数分解开单个数字，存储在新列表中，然后排序列表，输出最大和最小数，做差，然后再存储在新列表中，循环操作，看看最后是不是得到一个固定的值。

程序涉及的是中国电子学会编程等级考试四级知识点。

1.求解

即求解三位数的归敛结果，是什么样的数据。

参照四位数验证方法，程序设计（如图1）。

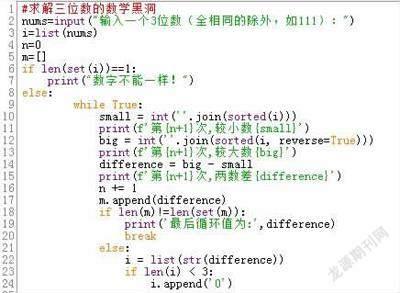
将输入的三位数转化为列表，然后判断数字是否完全相同，如果不完全相同，则循环执行将列表中的三个数字排序，取出最大和最小的数，做差，在屏幕上显示出来，同时添加到列表m中，如果有归敛结果，则会有重复数据，于是判断列表的长度和转换为集合后的长度比较，如果不相等，则输出最后一个数据，即为归敛结果。

比如输入：123，运行结果（如图2）。

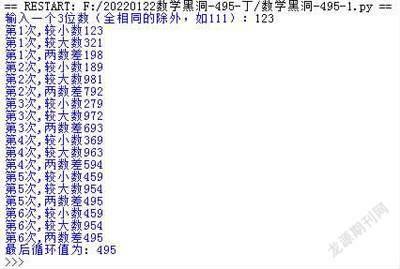
大家可以看到，归敛结果为495！那其他三位数也是归敛结果吗？下面我们来验证一下。

2.验证

即是输入任意一个数字不完全相同的三位数，进行验证，看看能不能得到495，需要几步。这里利用了自定义函数。

（1）递推法

输入一个三位数，但三个数字不能完全相同，将其转换为列表，排序、连接、转换出最大值和最小值，做差，再转换为列表，如果不够3位，则添加“0”，进行下一轮循环，直到得到“495”，然后输出转换用了多少次（如图3）。比如验证输入123，5次后获得结果495。

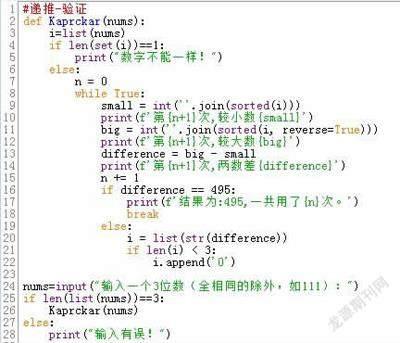
（2）递归法

递归与递推的不同之处，是调用了自身，达到循环的目的。过程和方法与递推类似。不同的是，递推算法中第7行的n=0去掉了，这是因为如果加上这行，每次调用自身的时候，n都会归0，不能计数，因而必须先设置n=0，然后在自定义函数中用“global n”。两种方法验证的结果是完全一样的（如图4）。

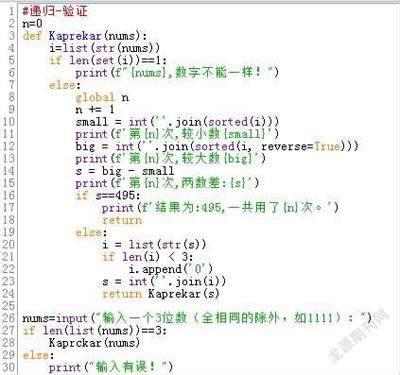
3.范围

即是验证一定范围内所有数字不完全相同的三位数，看看能不能得到495，在这个范围内需要最多的步数是多少。

（1）递推法

通过递推法验证（如图5）。

下面是在100-999范围内的递推法验证，即所有三位数的验证结果。在数字完全一样时，给出提示，从验证结果看，所有不完全相同的三位数，经过运算均可以得到“495”，并运算的最多次数是“6”（如图6）。

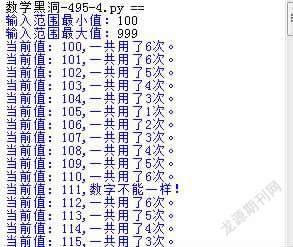
（2）递归法

递归法和递推法一样，也是在验证的基础上，验证一定范围内的所有整数，经过运算是不是都能得到“495”，并输出最多的运算次数。不同的是递归是通过调用自身，达到循环的目的。

同样，递归法需要将递推算法中的n=0去掉，而在遍历前设置n=0，然后在自定义函数中設置为“global n”。m为最大次数变量（如图7）。

下面是在100-999范围内的递归法验证，即所有三位数的验证结果。在数字完全一样时，给出提示，从验证结果看，所有不完全相同的三位数，经过运算均可以得到“495”，并运算的最多次数是“6”（如图8）。

我们看到，两种方法的验证结果是完全一样的。

通过验证，递推和递归方法得出的结果完全相同。这是在“6174”验证的基础上，修改程序后，比较容易得到的。那你注意到三位数和四位数在验证的时候，有什么相同点和不同点吗？

我们只用Python做了验证，有兴趣的老师和同学可以参考“6174”的方法用Scratch和APPInventor去验证。

本文是我自己的研究过程和心得，有不妥之处，请各位老师和同学斧正！