UUVs集群协同定位的分散式增广信息滤波方法

杜祯强，柴洪洲，向民志，章 繁，黄紫如，朱华巍

1. 自然资源部海洋测绘重点实验室，山东 青岛 266590； 2. 信息工程大学地理空间信息学院，河南 郑州 450001； 3. 中国电子科技集团公司第二十八研究所，江苏 南京 210007

随着水下勘探侦察、海洋工程、水下作业和水下作战等任务难度和复杂度的不断提升，水下无人航行器(unmanned underwater vehicle,UUV)以集群的形式互相协作成为UUV发展的必然方向[1-4]。自20世纪90年代中期开始，UUV协同定位就引起了许多西方国家的重视，美国、欧盟等开展了“The European GREX Project”[5]、“Autonomous Ocean Sampling Network”[6]等一系列项目。迄今为止，UUVs协同定位技术已经有了长足发展，并在海洋监测、资源探查及海军防御领域有着广泛的应用[7-9]。

协同定位与单UUV定位的最大区别是多个UUV之间可进行协调、合作与信息交互，如何用合理的数据融合算法有效地融合UUV内、外部传感器信息以及UUV之间的声学测距信息是实现UUVs集群协同定位的关键[10-11]。文献[12]首次提出了基于“移动长基线”的协同定位方法，并利用有人驾驶的母船通过声学通信设备实现了UUV的协同定位。文献[13]利用扩展Kalman滤波方法融合领航艇按时广播发送的参考位置坐标、协方差矩阵以及观测数据实现了UUVs协同定位。文献[14]和文献[15]分别提出容积卡尔曼滤波和无迹卡尔曼滤波的UUVs协同定位方法，解决协同定位中的非线性滤波问题。文献[16]提出了基于学生t-分布(Student 's t-distribution)的稳健滤波协同定位算法处理声速测量误差。高精度定位需要有符合系统特性的随机模型，但是由于观测受环境、信号等多种因素影响，先验权随机模型精度有限[17-18]。为了处理多径效应引起的量测厚尾噪声，文献[19]将最大相关熵应用到协同定位中。文献[20]在无多普勒测速仪(Doppler velocity log，DVL)或DVL受限情况下建立了协同定位的动态过程模型，通过海上试验验证了所建立的动态过程模型相比传统运动学模型在速度测量受限情况下的优势。文献[21]添加载体运动学约束，提出了适应复杂场景下的抗差渐消Kalman滤波。文献[22]和文献[23]分别提出顾及声线入射角的水下随机模型、顾及观测值时空相关性估计当前历元残差的方差协方差的随机模型。文献[24]采用自适应Huber滤波算法处理非高斯噪声的异常观测量。然而，以上研究主要致力于观测模型的精化和观测量噪声的处理，由于集群中各UUV互相观测后，状态参数相关所需要的庞大实时通信在实际中难以实现，均采用近似求解得到不严密的结果。

信息滤波作为Kalman滤波的对称形式，同属于高斯滤波，近年来在SLAM领域已得到广泛应用[25]。本文提出一种UUVs集群协同定位的分散式滤波(decentralized extend information filter,DEIF)方法，在顾及算法严密性的基础上有效地降低了通信载荷，实现了UUVs集群的分散式协同定位。

1 UUVs集群协同定位数学模型

1.1 协同定位原理

UUVs集群协同定位中主UUV通过搭载高精度的传感器实现自身高精度的定位，搭载低精度传感器的从UUV通过获取与主UUV之间的观测信息，实现观测资源的共享，从而对自身行位推算(dead reckoning，DR)位置进行校正，其原理示意图如图1所示。图1中椭圆表示误差椭圆，椭圆面积表示位置误差的不确定度，圆环的宽窄表示观测噪声的大小，从UUV根据主UUV的观测信息对自身行位推算误差进行修正，降低自身位置的不确定度。

图1 UUVs协同定位原理Fig.1 UUVs cooperative localization

假定UUVs集群由N个UUV构成，其运动状态的空间模型可表示为

(1)

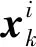
(2)

(3)

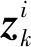
1.2 传统分散式Kalman滤波

对于UUVs集群，k时刻单平台的观测更新为

(4)

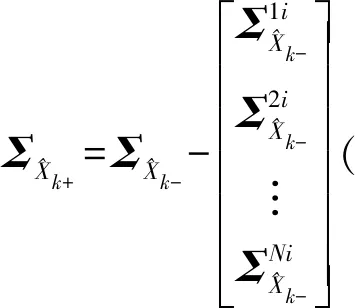
(5)

(6)

(7)

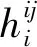
按照严密的理论要求，首先传统分散式Kalman滤波需要所有UUVs集群平台保持时间同步，不断发送/接收来自集群中每一个平台的信息，这导致庞大的实时通信量。其次观测更新只能依次进行，对于同一个时刻的观测，UUV集群在完成一个观测量的更新后，才能启动另一个观测量的更新。当UUVs集群规模增大，同一时刻的观测量增多，传统的分散式Kalman滤波在实际中难以实现。因此传统方法只能忽略平台之间的相关性，即观测更新只考虑观测量涉及的UUV平台，但这样的计算结果显然不是严密的。

1.3 协同定位的分散式增广信息滤波

(8)

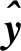
采用矩参数的高斯滤波即为Kalman滤波，采用信息参数的高斯滤波即为信息滤波，Kalman滤波与信息滤波仅为形式上的不同，但由于参数形式的不同使得处理不同问题会有不一样的复杂度。将k时刻单平台观测更新的Kalman滤波形式替换为信息滤波形式，即将式(8)代入式(5)

(9)

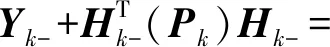
(10)

Yk+=Yk-+Ik

(11)

同理将k时刻UUVi单平台观测更新的Kalman参数替换为信息参数，即将式(8)代入式(4)，即

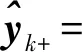
(12)

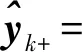
(13)

(14)

由式(13)和式(11)可以看出，在进行UUVi的单平台观测更新时，仅需要更新UUVi的信息参数。UUV单平台的观测更新仅与其自身有关，而不像传统方法单平台观测更新需要更新所有平台的状态参数。同理将k时刻UUVi对UUVj观测更新的Kalman滤波参数表达替换为信息滤波表达，即将式(8)代入式(7)，即

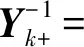
(15)

等式两边同时求逆，进一步化简整理得

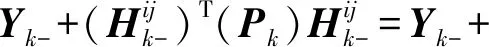
(16)

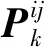
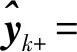
(17)

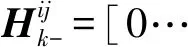
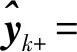
(18)

(19)

由式(18)可以看出，进行UUVi与UUVj的平台间观测更新时，仅需要对UUVi和UUVj的信息参数更新，而无须像传统方法对UUVs集群整体进行信息参数更新。对于UUVs集群协同定位，信息滤波的观测更新仅改变观测量直接涉及状态的信息参数，相比于传统方法的观测更新需要改变所有与观测相关的状态参数，信息滤波的观测更新具有局部性。

考虑到水下环境的复杂性和水声通信引起的时间延迟，交换信息滤波观测更新和时间更新的顺序，存储部分历史信息，即可得到增广信息滤波。UUVs集群进行状态添加即每个UUV平台各自进行状态添加，不同时刻UUV状态参数之间存在协方差，可按协方差公式推导得到。体现在马尔可夫随机场上，状态添加即为增加一个新的UUV状态结点，如图2所示。将新结点Ak+1连接到一个已有的结点Ak上，并且改变被连结点Ak的数值。

图2 UUVs状态添加Fig.2 State augmentation of UUVs

(20)

(21)

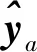
(22)

(23)

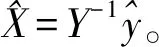
2 理论仿真分析

仿真时间设置为1800 s，观测间隔为1 s且每次仅能进行两两UUV之间的观测，水声测距标准差为1 m。海域水流速度为2 m/s，UUV航行速度为4节。3个UUV的轨迹路线如图3所示，黑线表示UUV的实际运动轨迹，绿线表示UUV航位推算轨迹。

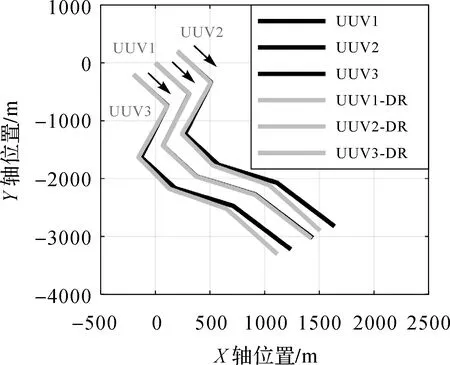
图3 UUVs的实际轨迹及航位推算轨迹Fig.3 Trajectory and dead reckoning trajectory of UUVs

对于搭载高精度INS和DVL的UUV A，其航位推算的误差要远小于UUV B和UUV C。状态添加时，同一时刻各UUV按照预定的编号(A、B、C)进行排序，每个时刻两个UUV之间进行观测。图4表示前5个时刻UUVs集群的状态添加及观测更新，实线表示UUV按照运动学方程进行状态添加，虚线表示两个UUV之间进行观测。

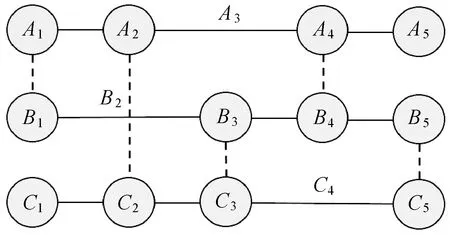
图4 前5个时刻UUVs的状态添加和观测更新Fig.4 UUVs state augmentation and observation update in the fifth epochs

对UUVs集群进行状态添加时，对应的信息矩阵Y的变化体现在两方面，一是信息矩阵维数的增大，且新增元素位于原矩阵的右侧和下方；二是原信息矩阵内的部分区域会发生改变。图5表示t=5时UUVs集群状态添加引起的信息矩阵变化。状态A5、B5和C5添加到已有的联合状态中，其中A5连接到A4,B5连接到B4,C5连接到C4。信息矩阵维数增加的部分来自新状态的添加，原有信息矩阵的变化位置为状态添加连接到节点的相应位置，红色区域和蓝色区域重叠的部分为信息矩阵需要修正的序列。

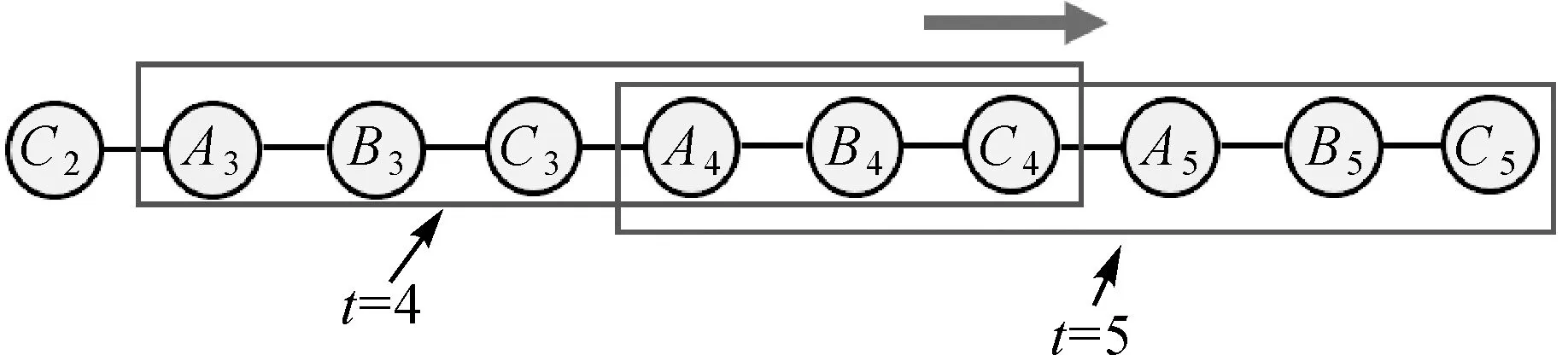
图5 t=5时状态添加引起信息矩阵Y的变化Fig.5 Change of information matrix Y caused by state augmentation in t=5

为进一步显示信息矩阵的变化，图6给出了对应上述状态添加的信息矩阵(a)及其Cholesky分解矩阵(b)。灰色表示该处矩阵值不为零，白色表示该处矩阵值为零。信息矩阵中5个红色方框分别对应5个时刻，方框内表示该时刻UUV所对应状态的信息矩阵，红方框外表示不同时刻间UUV所对应状态的信息矩阵。对于图6(a)第一个红色方框，UUV A和UUV B进行了相互观测，其信息矩阵相对应位置的元素不为零；UUV C状态与UUV A、B都不相关，其信息矩阵相应位置元素为零。

由Cholesky分解的性质，带状稀疏矩阵的Cholesky因子L保持带状性，仅原来带状区域内的部分零元素会变成非零元素。如图6所示，信息矩阵分解后的Cholesky因子矩阵依旧满足带状性。带状矩阵Cholesky分解具有局部性，使得UUVs集群的信息矩阵可以实现递增分解，并且每一步的计算量不随矩阵规模的增大而增大。图7表示UUVs集群信息矩阵的状态添加过程，图7(a)、图7(b)、图7(c)分别表示第3、4、5个时刻的UUVs的信息矩阵，图8表示与图7相对应的Cholesky分解矩阵。

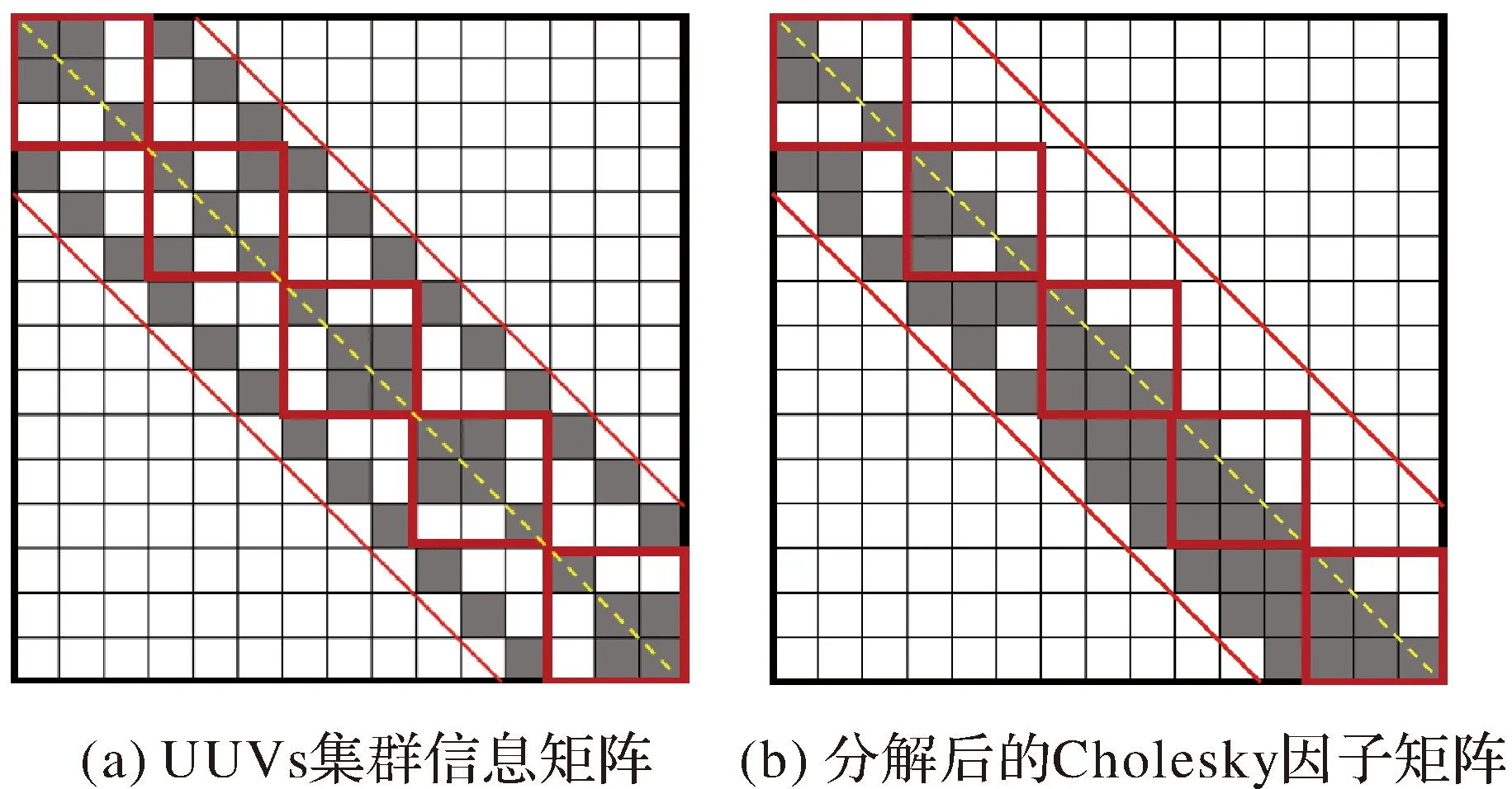
图6 UUVs集群信息矩阵及其Cholesky因子Fig.6 UUVs information matrix and Cholesky factor

将上述UUVs集群状态添加过程展开，图7(a)中橙色方框为t=3时刻的状态添加，图8(a)中蓝色方框表示图7(a)中信息矩阵相应位置的Cholesky分解。t=4时刻，UUVs状态添加如图7(b)所示，状态添加仅增加了橙色方框右侧和下侧的区域，其Cholesky分解后的结果如图8(b)所示，状态更新后的Cholesky分解并未改变原有位置的分布。信息矩阵中元素影响Cholesky分解的区域仅为其右侧和下方，即意味着每次状态更新仅需改变红色方框内的Cholesky因子即可，进而实现信息矩阵的递推分解。

图7 UUVs集群信息矩阵状态添加Fig.7 State augmentation of UUVs information matrix

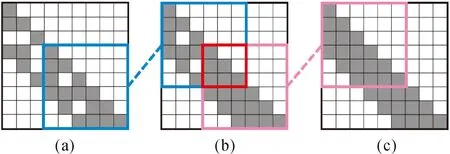
图8 UUVs集群信息矩阵Cholesky因子Fig.8 The Choresky factor of the UUVs information matrix

图9 传统分散式Kalman滤波的通信策略Fig.9 Communication strategy of traditional decentralized Kalman filter

图10 UUVs增广信息滤波的通信策略Fig.10 Communication strategy of UUVs extend information filter

图11为UUVs集群的真实轨迹，航位推算和分散式增广信息滤波的解算结果。图中黑线表示UUV的真实轨迹，绿线表示UUV的航位推算结果，红线表示本文方法的计算结果。可以看出，使用本文方法能够显著提高UUVs集群的定位精度。为进一步说明所提出的UUVs集群协同定位分散式增广信息滤波与集中式滤波的精度一致性，图12表示分别采用集中式扩展Kalman滤波和分散式增广信息滤波进行UUVs集群协同定位后UUV B和UUV C在X、Y方向的精度。

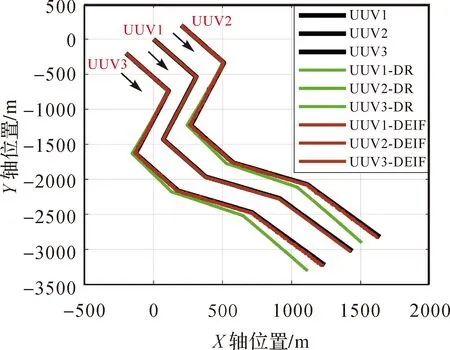
图11 UUVs的轨迹、航位推算及本文方法解算结果Fig.11 The trajectory and dead reckoning of UUVs and the results of the proposed method

图12(a)中绿线表示航位推算的结果，红线表示集中式Kalman滤波的结果，图12(b)红线表示本文方法的结果，两种方法的具体计算结果见表1。由表1可以看出，UUV2采用航位推算在X、Y方向上的误差RMS为54.82、35.27 m，采用集中式Kalman在X、Y方向上的误差RMS为5.67、4.92 m，采用本文方法在X、Y方向上的误差RMS为5.40、4.74 m。对于UUV3采用航位推算在X、Y方向上的误差RMS分别为59.07、31.95 m，采用集中式Kalman在X、Y方向上的误差RMS为6.10、4.87 m，采用本文方法在X、Y方向上的误差RMS为5.22、4.64 m。传统集中式Kalman滤波RMS和STD的平均值分别为5.39 m和3.28 m，分散式本文方法的RMS和STD分别为5.00 m和3.07 m。可以看出，分散式本文方法与集中式Kalman滤波保持精度上的一致性。

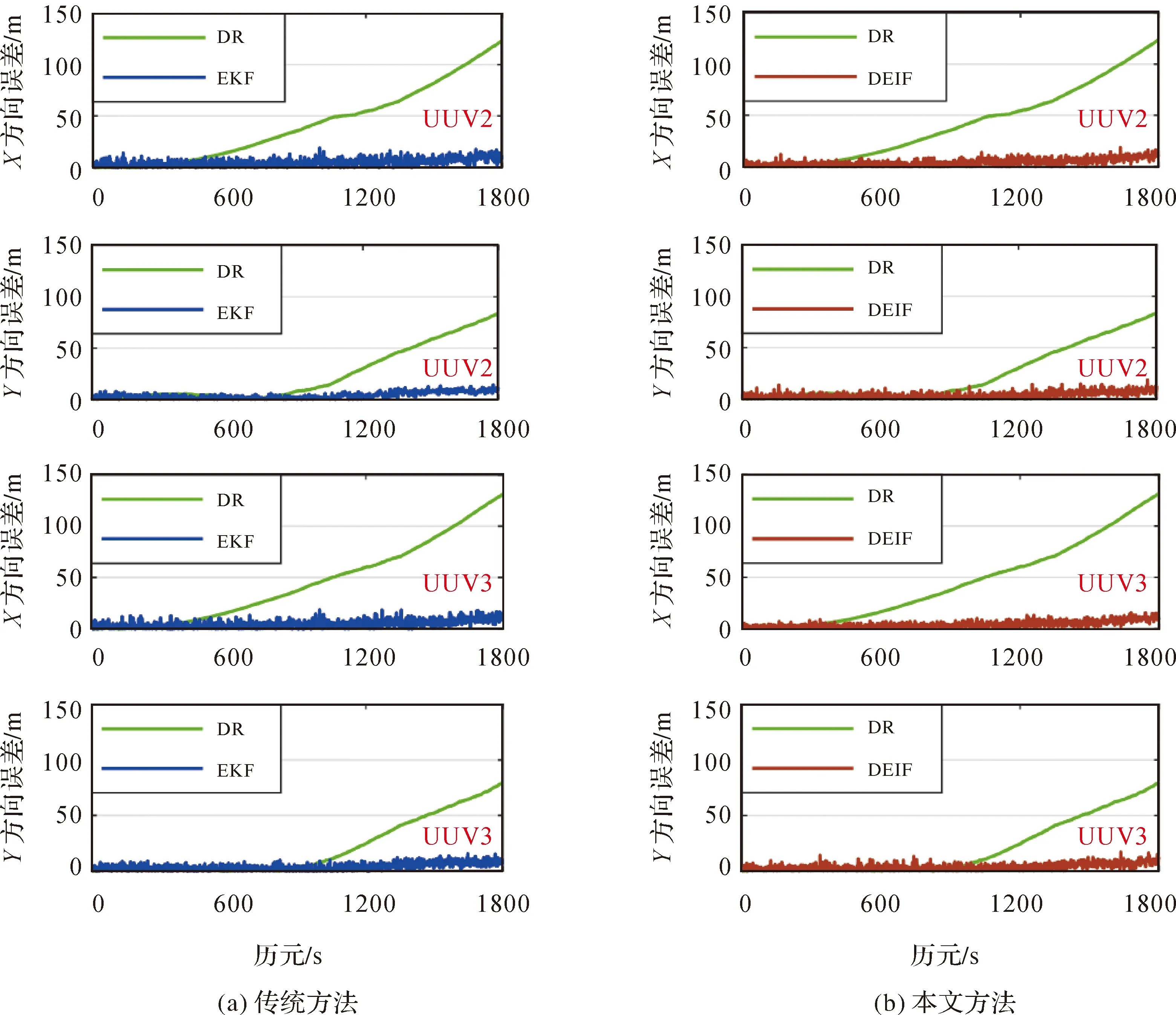
图12 传统集中式Kalman滤波与本文方法一致性对比Fig.12 Consistency comparison between traditional centralized Kalman filter and the proposed method

表1 分散式方法与集中式的Kalman滤波统计结果Tab.1 Decentralized new method and centralized Kalman filter statistical results m

3 结 论

针对水下复杂环境及UUV搭载水声传感器的特性，从高斯分布的角度构建了一种基于增广信息滤波的UUVs集群协同定位方法，解决了传统分散式Kalman滤波由于庞大通信限制无法得到严密结果的问题。每个UUV平台根据本地的传感器数据建立自己的状态链，同时广播自己的测距状态信息，各个平台协同完成修正序列的Cholesky修正。基于严密的数理理论证明了所提出的分散式滤波与集中式滤波的误差一致性，并与传统Kalman滤波进行对比分析。

理论仿真分析表明，分散式方法与集中式Kalman滤波保持精度上的一致性，且本文方法使得观测更新仅与观测直接涉及的UUV相关，有效地降低了通信载荷，实现观测信息的即插即用。