波导式偏振调制测距系统

高超纪荣祎高书苑董登峰周维虎*

波导式偏振调制测距系统

高超1，2，纪荣祎1，2，高书苑3，董登峰1，2，周维虎1，2*

（1.中国科学院 微电子研究所，北京 100094；2.中国科学院大学，北京 100049；3.常州大学 机械与轨道交通学院，江苏 常州 213164）

为消除体相位调制器工作过程中热效应对偏振调制测距精度的影响，提出了利用波导式相位调制器替代体相位调制器的全光纤波导式偏振调制测距方法。对波导式偏振调制测距系统进行原理分析，利用琼斯矩阵得出传输过程中测量光偏振态的变化规律，建立调制信号频率、偏振光强度与被测距离的函数关系。然后，进行了直波导相位调制器特性测试，验证其半波电压随调制频率在3.5～7 V之间变化，正反电光响应一致性为2%～3%。最后，构建波导式偏振调制测距系统装置并进行实验验证，重复性测试实验中测量平均误差为0.44 mm，测量重复性为0.54 mm，变距离实验中测量平均误差为0.39 mm。波导式偏振调制测距系统能够实现距离的有效测量，具有不产生热效应，结构简单等优点，在激光测距方面具有应用价值。

激光测距；波导相位调制器；偏振调制；保偏光纤

1 引言

近年来，我国载人航天、大飞机、高能粒子加速器、500米口径球面射电望远镜等大型装备和大科学工程建设过程中的精密装配，对大尺寸高精度测量技术提出了更高的要求，以激光跟踪仪、全站仪、激光测距仪等为代表的大尺寸高精度几何量测量装备发挥了重要作用。这些测量装备的关键是高精度激光绝对距离测量［1-2］。

激光绝对测距技术按原理可分为激光飞行时间测距和非飞行时间测距两类。激光飞行时间测距法又分为脉冲式激光测距［3-4］、相位式激光测距［5-6］及干涉法激光测距［7-8］。其中，脉冲式激光测距和相位式激光测距受限于时间或相位测量精度，系统测距精度在毫米甚至厘米量级，无法满足高精度测量需求。激光干涉测距法的测距精度可以达到微米量级，但系统复杂且对现场条件要求高，无法完全满足大尺寸工业测量的现场需求。飞秒激光测距法具有测量精度高、量程大的优点，但飞秒激光光源成本较高，且技术成熟度有待提升，在工业领域尚不能大范围使用［9-11］。1988年，瑞士Kern公司借鉴斐索旋转齿轮测光速原理提出偏振调制测距法，并在此基础上研制出ME5000型精密激光测距仪，其测量范围最远可达8 000 m，测距精度为±（0.2 mm+0.2×106D）［12］。瑞士Leica公司收购Kern公司后推出μ-Base型高精度绝对激光测距仪，该仪器在160 m全量程范围内的测量精度为±10 μm［13］。这两款仪器利用体相位调制器对偏振光进行扫频调制，通过检测反射光强度极值点的调制频率解算出被测距离。由于光强度测量精度高于时间和相位测量精度，且光偏振态在空间传输过程中受温湿度等环境的影响较小，因此偏振调制测距方法在大尺寸高精度测量领域有着广阔的应用前景。

目前，偏振测距技术专利主要掌握在瑞士Leica公司，国外研究多以设备测试和结构分析为主。国内2014年天津大学进行了偏振测距理论方法研究，使用NewPort公司4431型体相位调制器构建了空间光路测距系统，验证了偏振调制测距方法的可行性，利用光纤延迟线测得该系统的测距精度为±10 μm［14-16］。然而，体相位调制器需要几十伏的调制电压，由此产生的热效应会影响测距精度。2019年，中国科学院光电研究院基于QUBIG公司D7v-T3型体调制器研究了热致相位差对测距精度的影响及其补偿方法［17-18］，但该方法无法满足偏振调制测距的高精度需求，且外加温度控制装置导致系统庞大，实用性受到限制。

本文研究利用波导式相位调制器替代体相位调制器的可行性，首先分析了波导式偏振调制测距原理，利用琼斯矩阵推导了测量光偏振态变化，得出调制频率与被测距离的函数关系，然后分别对波导式相位调制器和偏振调制测距系统进行了实验验证。实验结果表明，波导式偏振调制测距系统可实现距离测量，具有结构简单、无热效应等优点，有利于实现小型化、低功耗设计。

2 电光偏振调制测距原理

2.1　铌酸锂晶体电光调制效应

偏振调制测距利用铌酸锂晶体电光效应对光的偏振态进行调制。电光效应是指电光晶体折射率在电场作用下变化导致透射光的传输特性发生改变，电光晶体折射率是外加电场的函数，其在0附近的泰勒级数展开式为：

式中：为线性电光系数（Pockels系数），为平方电光系数（Kerr系数）。

偏振调制测距利用电光效应中的一次线性关系，当施加电场与通光方向垂直进行横向调制时，线偏振光相移如下：

式中：为加载电压，为沿通光方向的晶体长度，为晶体沿电场方向的长度，0为真空中波长。

当线偏振光的偏振方向与调制电场成45°角时，只对平行于电场方向的偏振光分量调制，因此两偏振光分量经过电光晶体调制后会产生相位差Δ，即：

通常将Δπ时所需的电压定义为半波电压π，π与材料性质、光波长和晶体外形尺寸有关，是衡量调制器的重要参数。

对调制器施加正弦调制信号，测量光往返两次通过电光晶体时产生的相位差分别为：

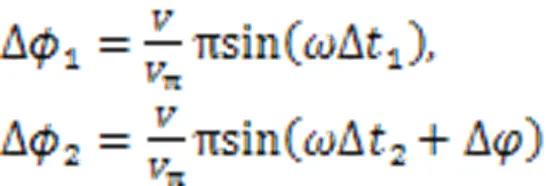
式中：Δ1和Δ2为测量光往返通过调制器的调制时间，Δ为测量光在测距空间往返飞行过程中调制信号的相位变化量。利用铌酸锂晶体的晶体对称性，合理设计系统测量光偏振态的变化，使光电探测器检测到的相位变化只与Δ相关，再利用Δ包含的飞行时间信息即可实现距离解算。

2.2　直波导相位调制器

基于铌酸锂电光晶体制成的相位调制器是偏振调制测距系统的核心器件，可分为体相位调制器和波导相位调制器，二者工作原理相同，但制作工艺不同。波导相位调制器是基于半导体工艺制成的集成光学器件，主要应用在光发射机、光纤陀螺及光纤传感等领域。这些领域中只需要单向通光，而偏振测距在测量光收发过程中需要正反双向通光，因此需要选取满足偏振调制测距系统使用需求的波导相位调制器。

波导相位调制器的制作工艺有质子交换法和钛扩散法两种，质子交换法只能工作在单偏振状态，钛扩散工艺调制器能够实现两种偏振态通光，具有低偏振相关损耗，满足偏振测距对两个偏振态分量进行调制的需求［19］。根据电极结构可分为集总参数电极、行波电极等，集总参数电极结构和电气参数具有对称性［20］，能够最大限度地保证正反通光过程中光电响应的一致性，因此选取基于钛扩散工艺制成的集总参数电极直波导相位调制器用于偏振调制测距系统，其结构如图1所示。在铌酸锂晶体衬底上扩散钛增加折射率，制成宽度为的波导带，集总参数单电极相对于波导中截面镜像对称，正负电极相对于波导镜像对称，利用T型耦合器将电极与调制信号源连接，施加电场可对波导内光信号的偏振态进行调制。电极自身阻抗很小，可等效为15～20 pF电容，需外接终端电阻实现调制器与信号源间的阻抗匹配。

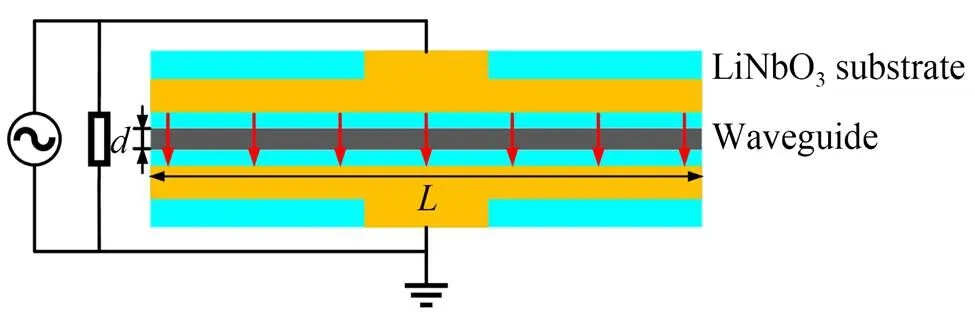
图1　直波导式相位调制器示意图

与体相位调制器需要对整个铌酸锂晶体进行调制不同，波导相位调制器只需对波导内光信号进行调制，波导宽度为微米量级，长度为厘米量级。根据式（3）可知，波导相位调制器具有较小的半波电压，商用产品的半波电压多在4 V左右，可避免热效应产生，降低系统功耗。

3 波导式偏振调制测距系统

结合直波导相位调制器工作原理，设计的波导式偏振调制测距系统结构如图2所示。该系统由光源、光纤隔离器、保偏光纤环形器、直波导相位调制器（EOM）、光纤1/4波片、准直扩束器、保偏光纤分束器（Polarized Beam Splitter，PBS）和光电探测器（Photodetector，PD）等构成。

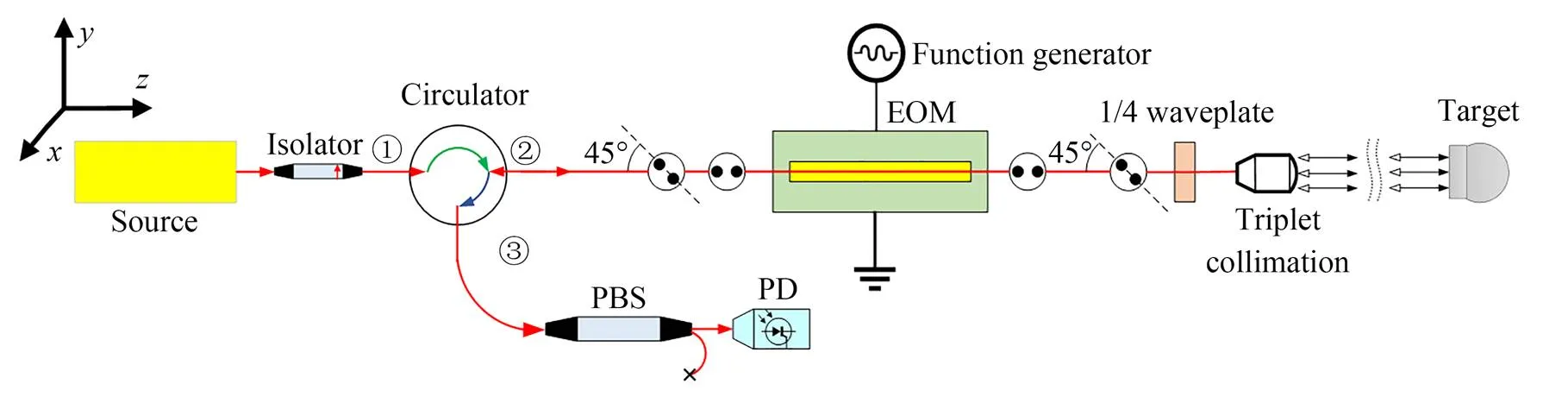
图2　波导式偏振调制测距系统结构

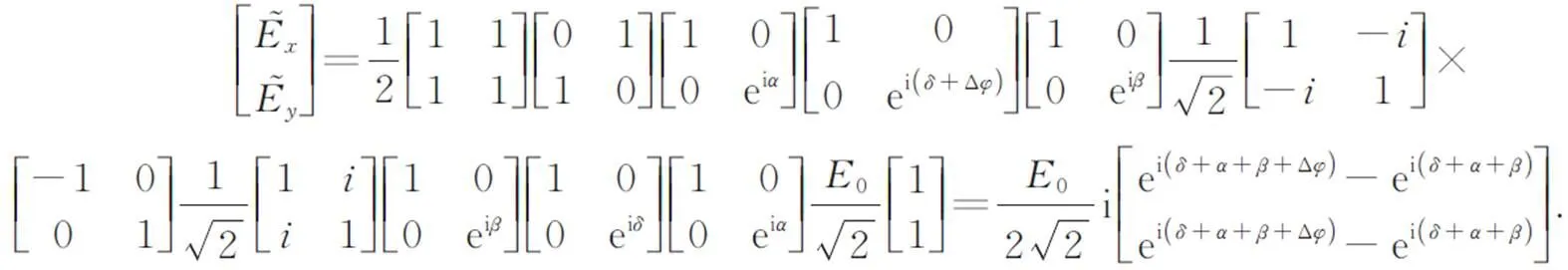
光电探测器检测到的偏振光光强如下［22］：

式（6）表明，光强度只与测距飞行过程中的调制信号相位变化量Δ成三角函数关系。为提升测距精度，避免进行反三角函数运算，选取Δ2π时刻光能量极值点进行空间距离解算。由于存在多周期导致的模糊距离问题，扫频调制得到连续两个光强极值点频率1，2，联立方程即可得到空间距离的计算公式：

式中：［］表示取整运算，为光速，1为零相差时半波长数。由式（7）可知，系统的测距精度和测量范围由极值点频率决定，因此光强极值点调制频率检测的准确性和调制信号源频率的稳定性对测距精度有重要影响。

4 实验与结果

4.1　直波导相位调制器特性测试

通过分析琼斯矩阵可知，调制器正反光电响应的一致性直接影响推导结果，选取的直波导相位调制器具有很好的结构对称性，但仍需对其电光响应特性进行实验验证。由于偏振调制测距只利用电光晶体的一次特性，因此可通过半波电压测试反映其电光响应特性。

由于对调制器进行高频信号调制时，信号源的输出功率会受到限制，因此实验系统利用正弦信号对电光调制器进行相位调制时在频谱上会产生边带，即光频梳［23-24］，如图3（a）所示。载波光能量、边带光能量与调制深度符合贝塞尔函数关系，如图3（b）所示。测得载波0和边带1的能量占比后，即可得到当前调制电压对应的调制深度，进而计算得到半波电压值，实现利用低压信号源测得高频调制下的半波电压。

图3　相位调制器调制波形

直波导相位调制器特性测试系统如图4所示，它由1 550 nm超窄线宽激光器（RIO MP-RIO-1550）、扫描式法布里珀罗干涉仪（Thorlabs SA210-12B）和射频模拟信号发生器（Keysight N5171B）等构成。

图4　相位调制器特性测试实验装置

由信号发生器在20，50，100，200，300，400，500，550 MHz固定频率点输出正弦信号，利用法布里珀罗干涉仪测量载波0和边带1的能量占比，计算得到半波电压，结果如图5所示。实验过程中用热成像仪（Fluke Ti110）监测调制器的壳体温度。

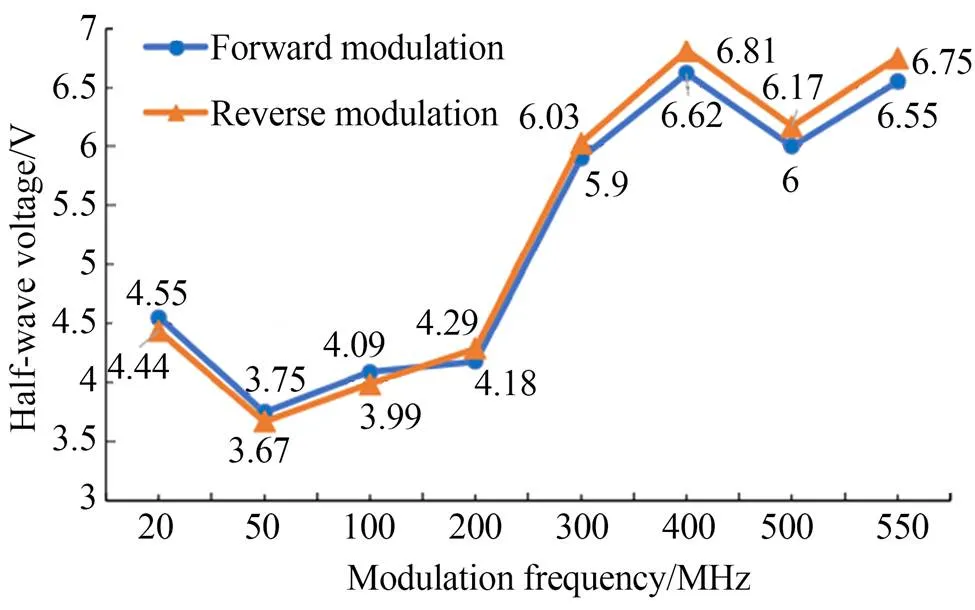
图5　相位调制器特性测试实验结果

由图5可知，相位调制器的半波电压随调制信号频率在3～7 V间变化，同频率下正反光电响应一致性为2%～3%，实验过程中壳体温度在28.9～29.2 ℃之间变化。实验结果表明，直波导相位调制器工作过程中未产生热效应，具有较低的半波电压和较好的正反电光响应一致性，能够满足测距系统的使用要求。但由于半波电压随调制器频率变化，为保证调制效果，需结合器件特性对调制信号进行分段设计输出。

4.2　测距实验

测距实验装置如图6（a）所示，以10 kHz步进在100～200 MHz内进行调制测试，测得实验数据如图6（b）所示，光强度与调制频率呈正弦关系。

图6　偏振调制测距系统及扫频波形

保证实验条件不变，利用固定长度光纤反射镜进行系统重复性测试。调制器到反射镜的光纤长度为8.15 m，光纤折射率为1.46～1.47，等效空间距离为11.899 0～11.980 5 m，实验过程中信号源以10 kHz步进在150～250 MHz输出正弦调制信号。本实验为单次重复性测距实验，在其他条件不变的情况下，重复扫描3次，如图6（b）所示，在100 MHz扫描区间有8个极大值，根据偏振测距计算公式，每相邻两个极值点即可得到一个距离值，因此每次扫描可以得到7个测量距离值，测试结果如表1所示。

表1150～200 MHz重复测试实验结果

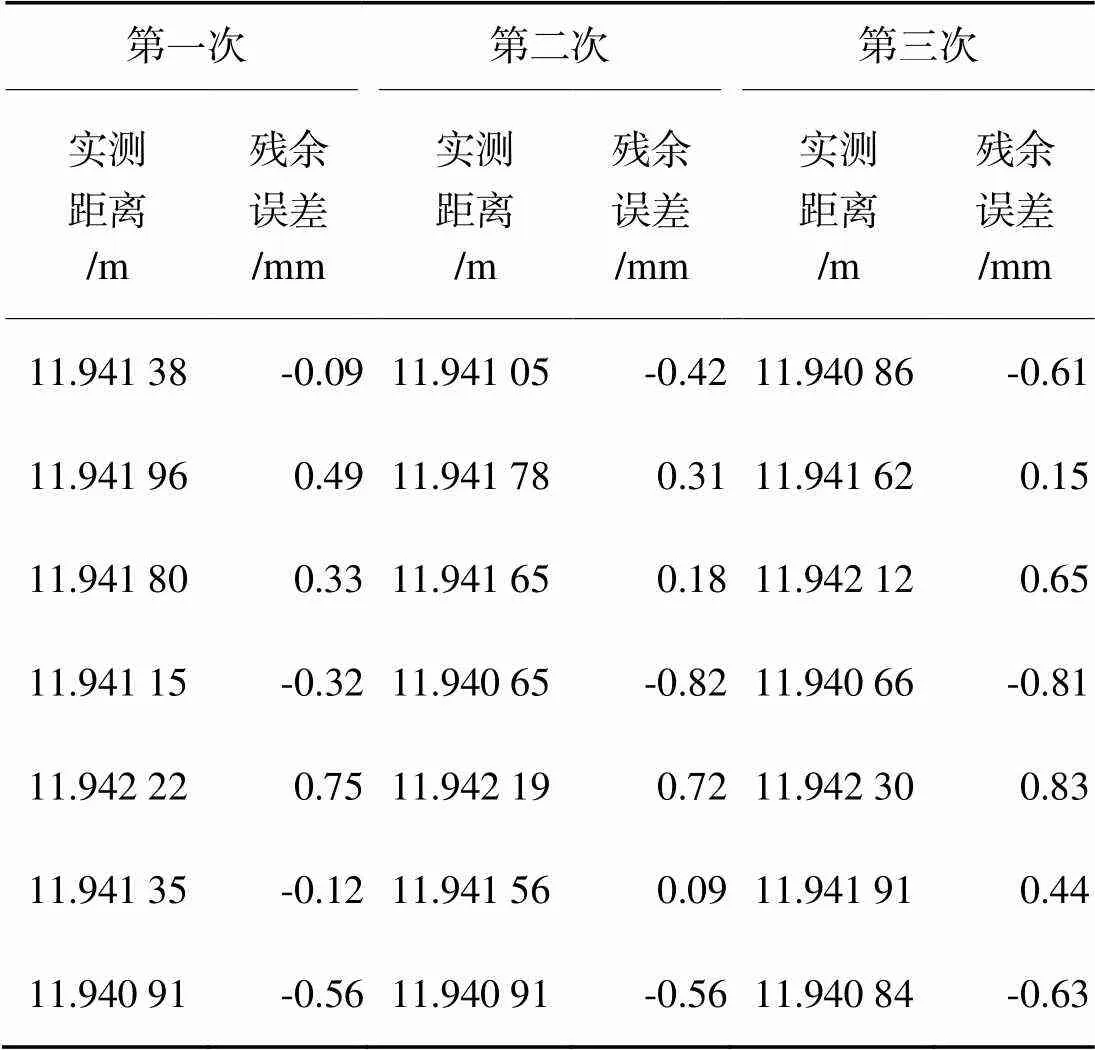
Tab.1　Result of repeated test at 150-200 MHz

3次重复测量结果相对独立，对21个实测距离值进行计算得到距离的算术平均值为11.941 47 m，以此为基础计算得到的残余误差如表1所示。系统测量平均误差为0.44 mm，重复性标准差为0.54 mm。

调制器特性测试实验表明，不同频率段器件电光响应不同，为验证调制频率对测距系统精度的影响，保持12 dBm的输出功率不变，以50 MHz间隔在100～500 MHz区间分频率段输出调制信号，测试结果如表2所示。

表2分区间测试实验结果

Tab.2　Result of different frequency separation test

为验证调制频率对测距精度的影响，未进行重复性测试。每个扫频区间只测得3个距离值，误差分析过程中用8个频率段的24次测量结果计算得到算术平均值为14.913 69 m，并在此基础上进行残余误差和标准差计算，以增加样本容量。表2表明，相同条件下，不同频率区间段测得的数据标准差不同，其中200～250 MHz区间段标的准差最小为0.01 mm，350～4 000 MHz区间段的标准差最大为0.69 mm，两个区间段的测试数据对比如图7所示。为便于比较，横坐标统一为频率调制范围0～50 MHz，图7显示在350～400 MHz区间段波形畸变比较严重，影响了极值点频率确定以及最终的距离解算精度。

图7　不同频率段测试波形对比

在光路系统中接入光纤延迟线，通过光纤延迟模拟空间距离变化，测试系统对距离变化的响应。延迟线采用莱特索斯LT-ODL-1500-1550型电动光纤延迟线，测量结果如表3所示。

表3变距离测试实验结果

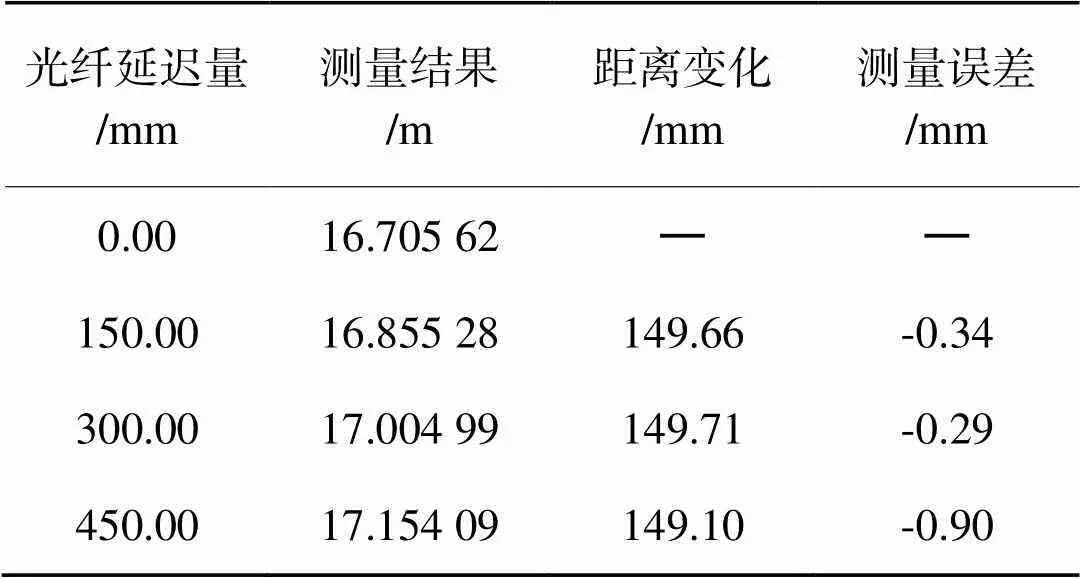
Tab.3　Result of different distance test

测量结果表明，波导式偏振调制测距系统能够准确测量光纤延迟线等效的空间距离变化。由于光纤延迟线精度为1.5 μm，高于本系统测量精度，以光纤延迟量作为距离变化的实际值，得到本系统空间距离测量的平均误差为0.39 mm。

5 结　论

针对偏振测距系统中体相位调制器在工作过程中产生热效应影响测距精度的问题，本文提出利用波导式相位调制器代替体相位调制器构建扫频偏振调制测距系统，对系统器件及测量光的偏振态变化进行了理论分析，得出调制频率、被测光强和被测距离的函数关系，通过实验验证了直波导相位调制的特性以及测距系统的可行性。波导式偏振调制测距实验装置的测量分辨率可以达到亚毫米量级，重复测量平均误差为0.44 mm，重复性标准差为0.54 mm，变距离测量的平均误差为0.39 mm。研究表明，波导式偏振调制测距系统在实现距离测量功能的同时，可以有效避免热效应对测量精度的影响，简化了系统结构，降低了系统功耗。

实验数据表明，扫描频率对测量结果有直接影响，因此接下来工作拟对调制器特性进行深入研究，合理匹配调制信号，优化极值点频率查找算法，提高系统测量精度，进一步提升波导式偏振调制测距系统的工程应用价值。

［1］ 李广云，范百兴. 精密工程测量技术及其发展［J］. 测绘学报， 2017， 46（10）： 1742-1751.

LI G Y， FAN B X. The development of precise engineering surveying technology［J］.， 2017， 46（10）： 1742-1751. （in Chinese）

［2］ GOLYGIN N K， LYSENKO V G， KHIZHNYAKOV V A. Metrological support for opto-electronic coordinate measurements［J］.， 2017， 59（10）： 1073-1077.

［3］ KILPELÄ A， PENNALA R， KOSTAMOV AARA J. Precise pulsed time-of-flight laser range finder for industrial distance measurements［J］.， 2001， 72（4）： 2197-2202.

［4］ 施智勇，潘晓声，张谦. 利用延时法进行高精度脉冲激光测距［J］. 光学精密工程， 2014， 22（2）： 252-258.

SHI ZH Y， PAN X SH， ZHANG Q. High-precision pulsed laser measuring distance by time delay method［J］.， 2014， 22（2）： 252-258. （in Chinese）

［5］ LIU Y Z， ZHAO B. Phase-shift correlation method for accurate phase difference estimation in range finder［J］.， 2015， 54（11）： 3470-3477.

［6］ 徐永垚，张铁犁，高小强，等. 激光绝对测距中相位信号的数字处理方法综述［J］. 宇航计测技术， 2020， 40（6）： 1-6.

XU Y Y， ZHANG T L， GAO X Q，. Review of digital processing techniques for phase signal in absolute distance measurement［J］.， 2020， 40（6）： 1-6. （in Chinese）

［7］ PAN H， QU X H， SHI C Z，. Resolution-enhancement and sampling error correction based on molecular absorption line in frequency scanning interferometry［J］.， 2018， 416： 214-220.

［8］ MEDHAT M， SOBEE M， HUSSEIN H M，. Distance measurement using frequency scanning interferometry with mode-hoped laser［J］.， 2016， 80： 209-213.

［9］ HYUN S， KIM Y J， KIM Y，. Absolute length measurement with the frequency comb of a femtosecond laser［J］.， 2009， 20（9）： 095302.

［10］ 纪荣祎，周维虎，黎尧，等. 激光跟踪仪高精度绝对测距系统［J］. 光学精密工程， 2016， 24（10s）：148-155.

JI R Y， ZHOU W H， L Y，. High absolute distance measurement system of laser tracker［J］.， 2016， 24（10s）：148-155. （in Chinese）

［11］ 谢建东，严利平，陈本永，等. 可调谐激光器激光波长宽范围自动偏频锁定［J］. 光学精密工程， 2021， 29（2）： 211-219.

XIE J D， YAN L P， CHEN B Y，. Automatic offset-frequency locking of external cavity diode laser in wide wavelength range［J］.， 2021， 29（2）： 211-219. （in Chinese）

［12］ DVOÁEKFILIP.［D］. Prague： Czech Technical University， 2012.

［13］ SABATKE D， HANDORF RVON， SULLIVAN J. Polarization and fold mirrors in application of the Leica Absolute Distance Meter［C］ .，， 2009， 7461： 74610N.

［14］ 黑克非，于晋龙，王菊，等. 基于二次偏振调制的变频测距方法与系统实现［J］. 物理学报， 2014， 63（10）： 62-67.

HEI K F， YU J L， WANG J，. Variable frequency range finding technology based on double polarization modulation method and system implementation［J］.， 2014， 63（10）： 62-67. （in Chinese）

［15］ 肖洋，于晋龙，王菊，等. 二次偏振调制测距系统中调制频率与测距精度的关系［J］. 物理学报， 2016， 65（10）： 44-48.

XIAO Y， YU J L， WANG J，. Relationship between modulation frequency and range accuracy in the double polarization modulation range finding system［J］.， 2016， 65（10）： 44-48. （in Chinese）

［16］ 王茜婷. 基于二次偏振调制的微波干涉激光测距系统研究［D］.天津：天津大学， 2019.

WANG X T.［D］. Tianjin： Tianjin University， 2019. （in Chinese）

［17］ 高书苑，黎尧，纪荣祎，等. 偏振调制测距系统频率漂移误差及其补偿［J］. 光学精密工程， 2019， 27（2）： 279-286.

GAO SH Y， LI Y， JI R Y，. Frequency drift error and its compensation in polarization modulation range-finding system［J］.， 2019， 27（2）： 279-286. （in Chinese）

［18］ GAO S Y， JI R Y， LI Y，. Compensation of frequency drift in frequency-sweep polarization-modulation ranging system［J］.， 2019， 9（6）： 1243.

［19］ 孔勇发，许京军，张光寅，等. 多功能光电材料——铌酸锂晶体［M］. 北京：科学出版社，2005.

KONG Y F， XU J J， ZHANG G Y，.-（LiNbO3）［M］. Beijing： Science Press， 2005. （in Chinese）

［20］ RAO A， FATHPOUR S. Compact lithium niobate electrooptic modulators［J］.， 2018， 24（4）： 1-14.

［21］ 廖延彪，黎敏. 光纤光学［M］. 2版. 北京：清华大学出版社， 2013.

LIAO Y B， LI M.［M］. 2nd Edition. Beijing： Tsinghua University Press， 2013. （in Chinese）

［22］ 郁道银，谈恒英. 工程光学［M］. 3版. 北京：机械工业出版社， 2011.

YU D Y， TAN H Y.［M］. 3rd Edition. Beijing： China Machine Press， 2011. （in Chinese）

［23］ PARRIAUX A， HAMMANI K， MILLOT G. Electro-optic frequency combs［J］.， 2020， 12（1）： 223-287.

［24］ 赵显宇，曲兴华，陈嘉伟，等. 一种基于电光调制光频梳光谱干涉的绝对测距方法［J］. 物理学报， 2020， 69（9）： 090601.

ZHAO X Y， QU X H， CHEN J W，. Method of measuring absolute distance based on spectral interferometry using an electro-optic comb［J］.， 2020， 69（9）： 090601. （in Chinese）

Polarization modulation range-finding system based on waveguide phase modulator

GAO Chao1，2，JI Rongyi1，2，GAO Shuyuan3，DONG Dengfeng1，2，ZHOU Weihu1，2*

（1，，100094，；2，100049，；3，，213164，），：

To improve the range-finding accuracy of a polarization modulation range-finding method and eliminate the thermal effect of bulk phase modulators， we propose waveguide phase modulators to substitute the bulk phase modulators. First， the polarization modulation range-finding method and system based on waveguide phase modulator were studied. The functional relationship between the frequency of the modulation signal， the intensity of the polarization light， and the distance was established by analyzing the polarization state change of light in the transmitted path of the system with the Jones matrix. Then， the characteristics of the waveguide phase modulator were tested. The test results show that the half-wave voltage ranges in 3.5-7 V and the consistency of the forward half-wave and backward half-wave voltages ranges in －2%-3%. Finally， a polarization modulation range-finding system with straight waveguide phase modulator was set up to verify the operation of the polarization modulation range-finding system. The average measurement error of the fixed-length fiber is 0.46 mm， and its measurement repeatability is 0.54 mm. The average measurement error is 0.39 mm according to a variable distance test. The experimental results demonstrate that this system can be employed for laser ranging. The system presents a simple structure that can help realize low power consumption and miniaturization.

laser ranging； waveguide phase modulator； polarization modulation； polarization maintaining fiber

O436.3；TH741.1

A

10.37188/OPE.2021.0381

1004-924X（2022）03-0246-10

2021-06-25；

2021-07-29.

国家重点研发计划资助项目（No.2019YFB1310100,No.2017YFF0107300）

高超（1983），男，河北秦皇岛人，博士研究生，高级工程师，2002年于北京航空航天大学获得学士学位，2009年于中国航空研究院获得硕士学位，主要从事光电精密检测、光纤传感等方面的研究。E-mail：gaochao@ime.ac.cn

周维虎（1962），男，安徽无为人，博士，研究员，博士生导师，1983年、2000年于合肥工业大学分别获得学士、博士学位，现为中国科学院微电子研究所光电研发中心主任，主要从事光电检测、光电系统总体设计与集成测试、光电精密测量技术与仪器等方面的研究。E-mail：zhouweihu@ime.ac.cn