不同围压条件下淤泥质黏土蠕变力学特性试验及模拟*

李 春，谭维佳

(1.重庆市建筑科学研究院有限公司，重庆400016；2.长安大学 地质工程与测绘学院，陕西 西安 710054)

淤泥质黏土是码头常见地基土，在应力作用下不仅会瞬间发生变形，还会随着时间推移而累积蠕变变形，威胁码头工程的长期稳定和安全[1-2]。研究淤泥质黏土蠕变特性，对控制淤泥质黏土地基沉降具有重要的工程意义[3]。

目前对于淤泥质黏土蠕变特性研究已有一定成果，李军世等[4]以上海淤泥质黏土为研究对象，选取合理经验参数，建立具有适用性的Singh-Mitchell蠕变经验模型；朱登峰等[5]对淤泥质黏土进行循环蠕变试验，研究蠕变应变特征和孔压变化规律；Wang等[6]开展天津滨海地区淤泥质软黏土蠕变试验，基于元件模型建立了非线性蠕变本构模型；赖华辉[7]研究不同干密度下的膨胀土蠕变特性，分析干密度对蠕变变形、蠕变速率、长期强度的影响；李硕等[8]研究上海淤泥质黏土固结蠕变过程中水和微机构变化规律，为淤泥质黏土宏观蠕变研究提供微观参考依据。

本文以某遮帘式板桩码头工程淤泥质黏土为研究对象，制备饱和重塑样，开展固结排水三轴压缩蠕变试验，分析淤泥质黏土应变特征、蠕变速率和等时轴压-轴向应变关系，结合淤泥质黏土的等时轴压-轴向应变双曲线形态特征，分别引入Mesri和Log-Modified模型辨识蠕变数据，给出两者模型参数求解方法，分别得到适用于本文淤泥质黏土的Mesri和Log-Modified蠕变经验模型，对比两者蠕变经验模型辨识效果，给出本文码头工程淤泥质黏土的推荐蠕变模型。研究成果可为淤泥质黏土蠕变特性研究及码头地基设计、施工及后期运营提供一定参考。

1 淤泥质黏土蠕变试验

1.1 试验材料及方案

本文淤泥质黏土取自某遮帘式板桩码头工程，其基本物理力学参数见表1。蠕变试验之前，根据取样深度完成先期k0不等向固结条件(k0为土的静止侧压系数)，取k0=0.5。

表1 淤泥质黏土基本物理力学参数

根据《土工试验方法标准》[9]，制备直径39.1 mm、高80 mm的饱和重塑样，蠕变试验采用SR-6型土体三轴流变试验机，蠕变试验方案见表2。

表2 蠕变试验方案

由表2可看出，本文试验分为两步：1)固结。首先对重塑饱和土样施加围压，完成等向固结后再依据先期k0固结条件，将轴向荷载缓慢加至目标值，完成k0不等向固结。2)蠕变。依据表2的试样方案控制轴压和围压的变化，蠕变稳定后再施加下一级轴向荷载直至破坏，每一级加载均维持在90 h以上，本文淤泥质黏土在第5级加载时破坏，3种围压下的破坏偏应力(σ1-σ3)f分别为300、400和500 kPa。为便于后文蠕变模型辨识及参数求取，再进行固结排水三轴压缩试验，确定3种围压条件下的剪切强度，分别为523、736和945 kPa。

1.2 试验结果

蠕变试验数据由三轴试验机数据系统采集，得到分级加载全过程曲线，如图1所示。

图1 逐级轴向加载蠕变曲线

由图1可看出，3种围压下的蠕变曲线轴向应变存在一个初始值，这是由于淤泥质黏土蠕变试验是完成先期不等向固结后进行的。蠕变试验中，淤泥质黏土在轴压提升的短暂时间内，轴向应变瞬间增大，这部分轴向应变为瞬时应变。随着加载时间的增长，土样表现出衰减蠕变行为，应变率逐渐降低，应变率趋于稳定后土样便进入了稳定蠕变阶段，土样在衰减和稳定蠕变阶段的轴向应变为蠕变应变。

2 试验结果分析

2.1 分别加载蠕变曲线

通过Boltzmann线性叠加原理[10]处理后的分级加载蠕变曲线如图2所示。

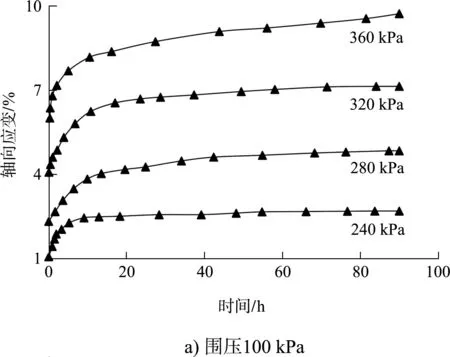
图2 分级加载蠕变曲线

由图2可看出，淤泥质黏土不同围压不同加载等级下的蠕变曲线形态较相似。同一围压下，随着轴压的提升，轴向应变逐渐递增。同一加载等级下，围压和轴压的升高促进轴向应变的增长。

2.2 蠕变速率

蠕变速率求取引用文献[11]中的计算方法：

(1)

式中：εn为蠕变应变；n为蠕变试验应变数据个数；Δε为蠕变应变差值之和；Δti为蠕变时间；vi为蠕变速率。

利用式(1)在图2的基础上进行计算，绘制蠕变速率曲线，如图3所示。

由图3看出，蠕变速率曲线分为衰减和稳定蠕变阶段两个部分，衰减蠕变阶段存在一个较高的初始蠕变速率，在10 h内逐渐衰减，接着进入稳定蠕变阶段，10～90 h蠕变速率基本保持恒定。在同一围压下，随着加载等级的提升，衰减和稳定蠕变阶段的初始蠕变速率和稳态蠕变速率均逐渐增大。

图3 分别加载蠕变曲线

为研究初始蠕变速率、稳态蠕变速率与围压、轴压之间的关系，选取图3中的稳态蠕变速率平均值及初始蠕变速率，绘制相对应的曲线如图4所示。

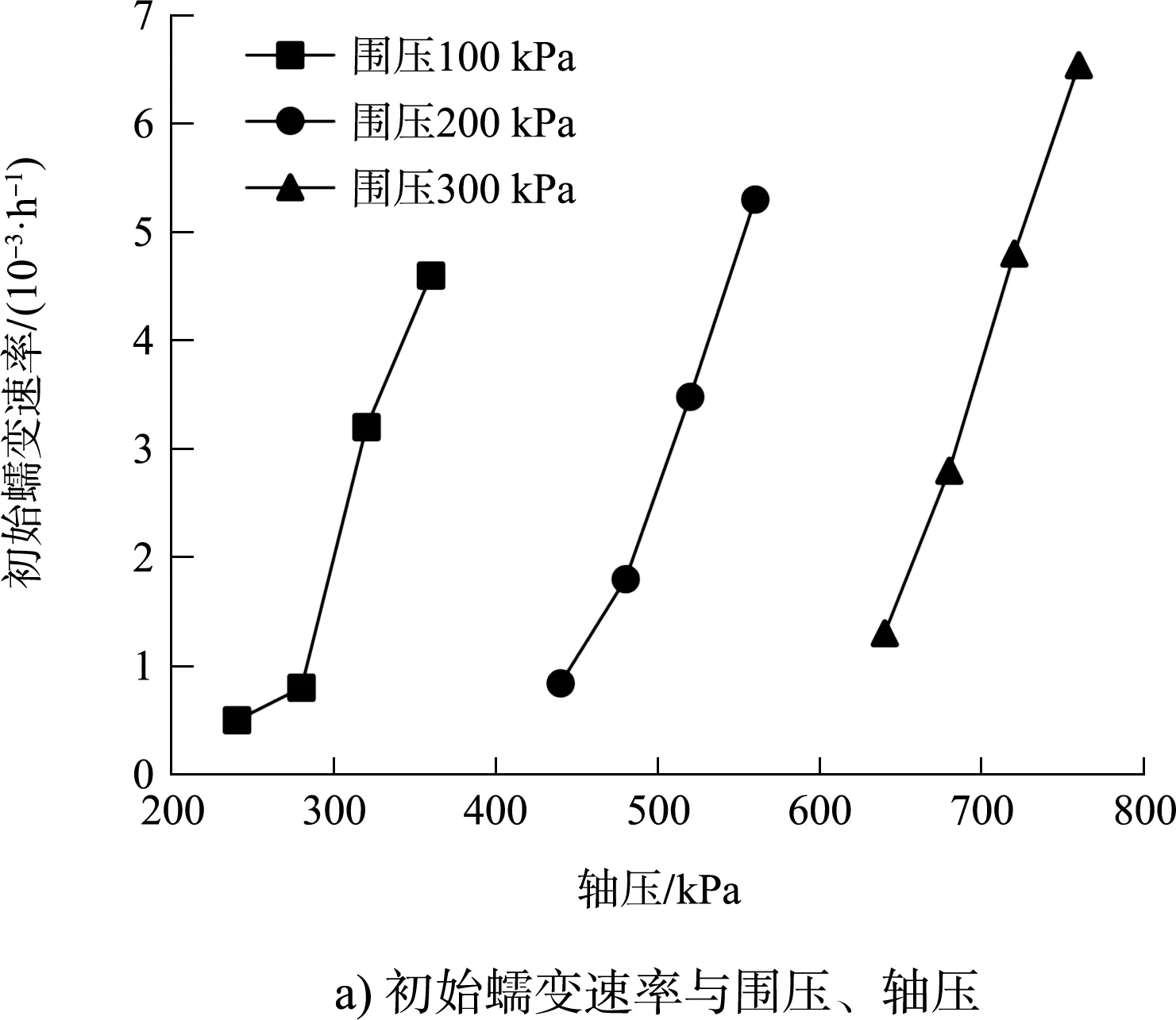
图4 初始、稳态蠕变速率与围压、轴压关系曲线

由图4a)可看出，在围压100 kPa、轴压240 kPa下，初始蠕变速率最小，仅为0.502×10-3/h；在围压300 kPa、轴压760 kPa，初始蠕变速率最大，达到6.538×10-3/h。在同一围压下，初始蠕变速率随着轴压的增大呈线性递增趋势。在同一加载等级下，较高轴压和围压条件下初始蠕变速率始终大于较低轴压和围压条件，这说明应力水平的提升会增高初始蠕变速率。由图4b)可看出，稳态蠕变速率与围压、轴压之间的变化规律与初始蠕变速率较为相似，在围压100 kPa、轴压240 kPa下，稳态蠕变速率最小，为0.007×10-3/h；在围压300 kPa、轴压760 kPa，稳态蠕变速率最大，达到0.890×10-3/h。在同一加载等级下，较高轴压和围压条件下稳态蠕变速率始终大于较低轴压和围压条件，这说明应力水平的增高使稳态蠕变速率增大。

2.3 等时刻轴压-轴向应变曲线

在图2中选取0.1、10、20、30、40、50、60、70、80和90 h共10个时刻的轴压-轴向应变数据点，绘制等时轴压-轴向应变曲线，如图5所示，限于篇幅，仅以淤泥质黏土围压100 kPa为例。选取3种围压下0.1和90 h时刻的轴压-轴向应变数据点，绘制不同围压下等时轴压-轴向应变曲线，如图6所示。

图5 等时轴压-轴向应变曲线

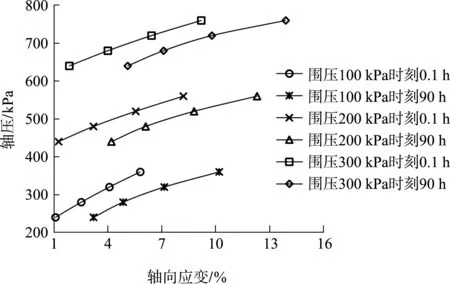
图6 不同围压下的等时刻轴压-轴向应变曲线

由图5看出，等时轴压-轴向应变曲线由0.1 h时刻的曲线和10～90 h曲线簇组成，0.1 h时刻的曲线近线性，10～90 h曲线簇具有明显的非线性特征，随着轴向应变的增长，曲线簇表现出逐渐靠拢应变轴的趋势。综合图5、6可看出，等时轴压-轴向应变曲线0.1 h时刻曲线近似线性，10～90 h时刻曲线簇形态近似双曲线。

3 淤泥质黏土蠕变经验模型

3.1 经验模型理论

目前Singh-Mitchell和Mesri经验模型在土体蠕变分析中应用较广，文献[12]在Mesri模型的基础上改进得到Log-Modified经验模型。其中Mesri和Log-Modified经验模型的应力-应变关系式一致，均为双曲线型，Singh-Mitchell经验模型的应力-应变关系式为指数型，由于Singh-Mitchell模型被证明不适用于低应力水平下蠕变行为模拟[13]，而Mesri和Log-Modified经验模型的应力-应变关系式与本文淤泥质黏土等时轴压-轴向应变较吻合，故本文分别引入Mesri和Log-Modified模型辨识淤泥质黏土的蠕变力学行为，Mesri和Log-Modified模型本构方程分别见式(1)(2)：

(2)

(3)

式中：ε为蠕变应变；t为蠕变时间；Eu为初始切线弹性模量；σ1为轴压；σ3为围压；(σ1-σ3)f为蠕变试验中的破坏偏应力；D为每一级加载轴压与三轴固结排水试验中剪切强度之间的比值；Rf为破坏比；a、b和c均为模型参数；t1为初始蠕变的参考时间，本文取t1为1 h；m为待定参数。

Mesri和Log-Modified模型共同的应力-应变关系式为：

(4)

式中：ε1为应力-应变关系中的应变。

Mesri模型的应变-时间关系式为：

(5)

Log-Modified模型的应变-时间关系式为：

ε2=(a+bt)c

(6)

式中：ε2为应变-时间关系中的应变。

两者模型求取时，应力-应变关系参数与时间关系参数分别求解，两者的应力-应变关系参数相同。

3.2 应力-应变关系参数求解

为了便于参数求解，变形式(4)为：

(7)

式(7)中的ε1/D与ε1线性相关，Rf为斜率，(σ1-σ3)f/Eu为截距。选取0.1～90 h共10个时刻的蠕变数据，以围压100 kPa为例，绘制不同时刻下ε1/D-ε1的关系曲线，如图7所示，为观察方便，省去部分时刻的数据。应力-应变关系参数见表3，限于篇幅，仅给出围压100 kPa下的参数取值。

图7 不同时刻下的ε1/D-ε1曲线

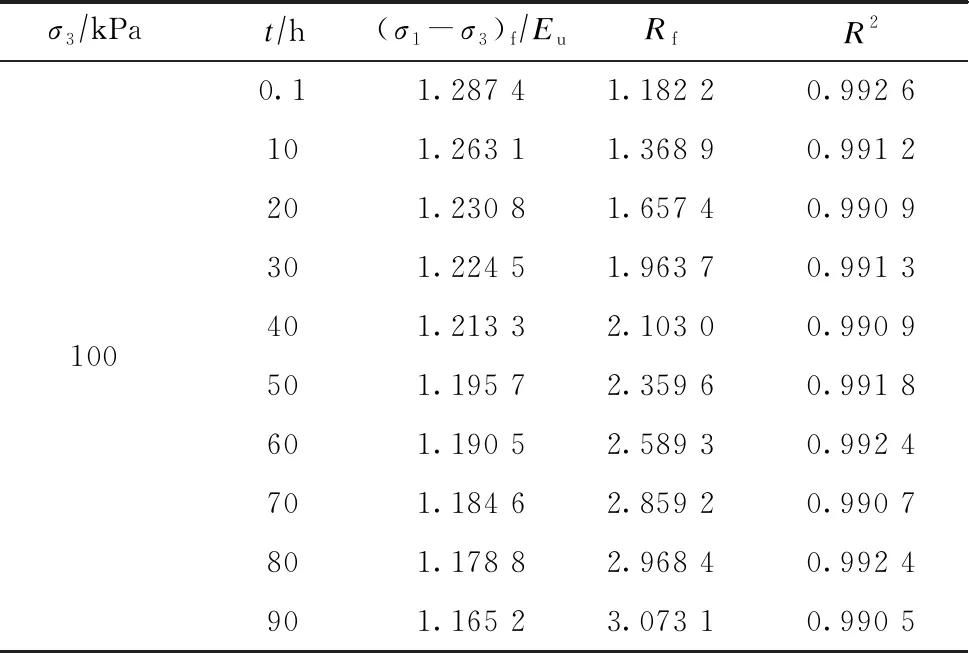
表3 应力-应变关系参数

由表3可看出，(σ1-σ3)f/Eu随时间增长呈递减趋势，Rf随时间增长呈递增趋势。通过式(7)线性拟合求解的方法得到不同时刻下的(σ1-σ3)f/Eu和Rf的平均值，见表4。

表4 应力-应变关系参数平均值

由表4可知，(σ1-σ3)f/Eu和Rf平均值均随着围压增大而递减，Eu随着围压增大而递增。

3.3 Mesri模型应变-时间关系参数求解

式(5)等号两边取对数可得：

lnε2=mlnt

(8)

由式(8)可看出，lnε2与lnt线性相关，m为该线段的斜率，于是绘制lnε2-lnt曲线，以围压100 kPa为例，如图8所示，应变-时间关系参数见表5。

图8 lnε2-lnt曲线

表5 Mesri模型应变-时间关系参数

由图8可看出，lnε2-lnt线性拟合较好，R2的平均值达到0.950 7。通过式(8)线性拟合求解的方法得到不同时刻下的m的平均值，见表6。

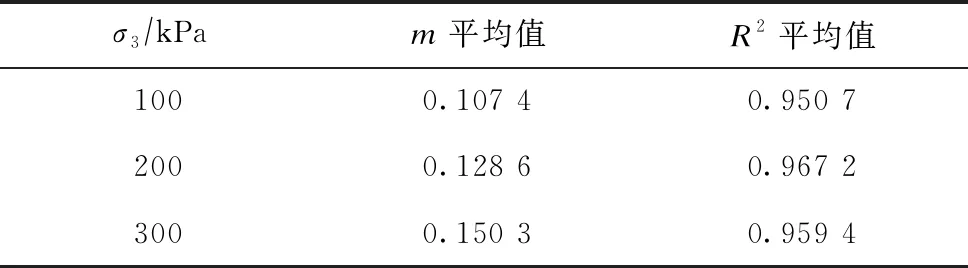
表6 参数m平均值

分析式(7)(8)发现，(σ1-σ3)f/Eu、Rf和m与轴压和时间无关，均通过线性拟合求解的方法确定，故取不同加载等级下(σ1-σ3)f/Eu、Rf和m平均值作为Mesri经验模型参数，将表4、6中相关参数代入式(2)可得：

(9)

式(9)即为本文淤泥质黏土在σ3=100 kPa下的Mesri蠕变经验模型。

3.4 Log-Modified模型应变-时间关系参数求解

通过数学软件Origin对图2蠕变数据进行拟合，算法采用一般的非线性最小二乘法，取参数a、b和c的平均值见表7。

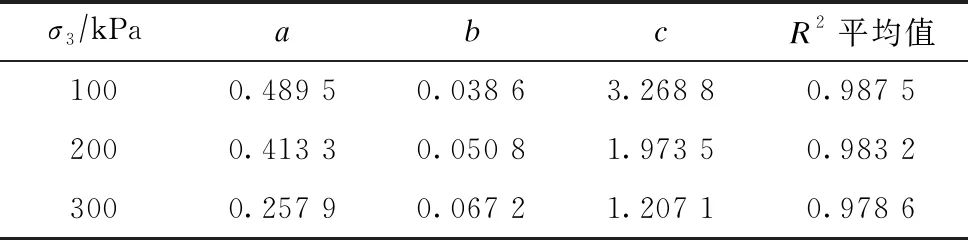
表7 参数a、b和c平均值

将表7中参数a、b和c的平均值及表4中(σ1-σ3)f/Eu和Rf平均值代入式(3)可得：

(10)

式(10)即为本文淤泥质黏土在σ3=100 kPa下的Log-Modified蠕变经验模型。

4 模型参数求解及验证

以σ3为100和300 kPa的试验数据为例，对本文Mesri和Log-Modified蠕变经验模型进行对比模拟验证，经验值与试验值对比曲线如图9所示。

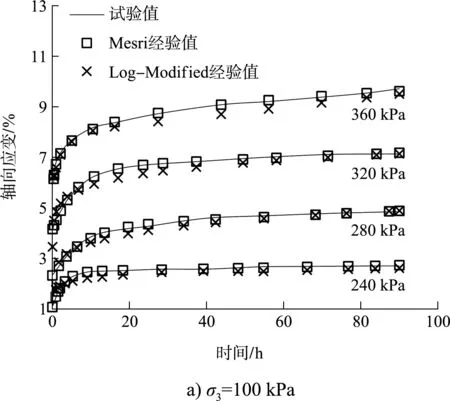
图9 经验值和试验值对比曲线

由图9可看出，Mesri蠕变经验模型辨识能力较强，拟合精度较高，R2平均值为0.990 5，而Log-Modified蠕变经验模型的经验值总体上低于试验值，拟合效果一般，R2平均值为0.954 7。工程实践中，若采用Log-Modified蠕变经验模型预测计算淤泥质黏土地基长期沉降及稳定性，在更长时限范围内，可能会造成较大误差，造成潜在的安全隐患。Mesri蠕变经验模型能较好地描述本文淤泥质黏土蠕变特性，将其作为本文淤泥质黏土的推荐模型。

5 结论

1)本文开展淤泥质黏土固结排水三轴压缩蠕变试验，淤泥质黏土在加载时瞬间弹性变形，随后依次进入衰减、稳定蠕变阶段。同一围压下，随着轴压的提升，轴向应变逐渐递增。同一加载等级下，围压和轴压的升高促进轴向应变的增长。

2)在同一围压下，随着加载等级的提升，淤泥质黏土初始蠕变速率和稳态蠕变速率均呈线性递增趋势。在同一加载等级下，较高轴压和围压条件下初始、稳态蠕变速率均始终大于较低轴压和围压条件。淤泥质黏土等时轴压-轴向应变曲线近似双曲线，具有明显的非线性特征，随着轴向应变的增长，曲线簇表现出逐渐靠拢应变轴的趋势。

3)结合淤泥质黏土的等时轴压-轴向应变双曲线形态特征，分别引入Mesri和Log-Modified模型来辨识蠕变数据，给出两者模型参数求解方法，得到适用于本文淤泥质黏土的Mesri和Log-Modified蠕变经验模型，通过对比发现Mesri蠕变经验模型辨识效果优于Log-Modified蠕变经验模型，R2平均值达到0.990 5，将Mesri蠕变经验模型作为本文淤泥质黏土的推荐模型。