面向时变回诊患者需求的急诊周排班研究

王子翔， 吴泽锐， 刘 冉

(上海交通大学 工业工程与管理系，上海 200240)

急诊服务主要是对突发疾病、意外损伤等急诊患者提供医疗服务[1]，一般由医院急诊科承担，为急诊患者提供7×24 h持续服务.近年来急诊医疗需求的大量增加，急诊科室的严重拥堵引起的急诊服务质量下降是普遍面临的问题.

急诊科室拥堵的原因是多方面的，一个重要原因是患者无法预约且到达率高度时变.以武汉市某医院为例，一天中急诊患者到达率在夜间较低，在上午5点左右剧增，7点到达第1个高峰，随后患者到达率下降并于11点再次剧增，并在约下午2点到达第2个高峰.面对需求的时变、随机特性，急诊科常规采用的仅区分日间、夜间的排班往往难以在高峰时段提供充足的人员，继而造成拥堵.同时，患者回诊是导致拥堵的重要原因.由于医生一般需要检查结果(如血检、B超、X光等)作为医疗决策的依据，所以大量患者必须经过一项或几项检查后回到医生处再次问诊，才能完成诊疗.患者甚至需要经历多次检查、问诊.时变、随机到达的回诊患者与初次到达患者相叠加，成为加剧急诊科室拥堵的重要因素.

为了缓解急诊科室拥挤，灵活的柔性排班方案被提出并已被部分医院采纳.不同于传统的排班方案(如8:00—16:00、16:00—24:00、24:00—8:00固定三班制)，柔性排班的可用班次更多，相比于传统的排班方案，每个医生可被安置的上班班次更加多样灵活，通过在高峰时段安排更多的医生，能够缓解拥堵问题.虽然柔性排班具有显著优点，但是如何针对患者的到达规律、考虑大量回诊现象而设计出科学合理的医生柔性排班方案却较为困难.首先，其备选班次多，比传统方式更加复杂.同时，急诊非常关注患者是否能够及时得到治疗，即患者的候诊时间等指标，如何采用柔性排班准确有效地减少患者的等待时间需要深入探讨.

本研究与多个研究领域相关.首先是医护人员的排班问题，对该问题建立数学规划模型是常用方法[2-4]，求解方法包括精确和启发式算法.精确算法包括使用求解器如CPLEX[5]、Branch-and-Cut[6]和Branch-and-Price[7]等.启发式算法包括模拟退火算法[8]、遗传算法[9]、禁忌搜索算法[10]、基于列生成的启发式算法[11]等.精确求解算法的优点在于能够求解问题的最优解，缺点在于其求解规模受限，而启发式算法则可以在较短时间获得大规模问题的可行解.

医护人员的排班问题中患者等待队长、等待时间等常作为目标函数或模型约束，因此需要对其进行解析计算评估.由于对此类时变排队系统建模具有挑战，常用的方法是基于稳态排队论的近似建模方法.文献[12]使用SIPP(Stationary Independent Period-by-Period)方法研究了时变服务系统的建模问题，通过将长时间段划分为若干时段，将每个时段的系统近似为稳态系统，完成长时段服务系统建模.文献[13]同样将长时间段分割，将每个分割时段的系统近似为稳态系统，给出了时变排队系统中顾客等待时间的评估方法，并在此基础上研究了以最小化患者总等待时间为目标的医生排班问题.文献[14]使用逐点稳态(PSA)法研究了时变服务系统的建模问题，该方法假设在任何时间点排队系统几乎都能立即到达稳态，对每个时间点的系统使用稳态排队系统加以近似以完成长时间服务系统建模.其他常使用的时变排队系统建模方法是仿真方法[15-16]和样本均值近似方法.文献[17]考虑了时变、存在回流客流的急诊患者需求，使用样本均值对急诊患者的等待时间进行近似评估，进而建立了混合整数规划模型求解医护人员的排班方案.文献[18]同样使用样本均值近似方法对考虑时变、带回流客流的门诊预约和非预约患者的等待时间进行解析建模.其他方法如数值方法[19]、无限服务台近似[20]、流模型近似[21]等方法也都曾被用于时变排队系统的建模研究.

尽管已有许多医生排班和医院排队系统建模的相关研究，由于时变的回流患者与初次到达患者的叠加效应和不同医疗服务流程的相互影响，考虑医院时变、带回流客流的排队服务系统的医生排班优化非常具有挑战性.仅有文献[22]研究了类似的时变、带回流系统，并结合简单的平方根规则给出了医生配置方法.

针对时变、带回流患者需求的急诊医疗服务系统，提出新的准确患者队长的解析计算方法，在给定医生排班的情况下，迅速且准确地评估每个时段患者等待队长.在此基础上，建立医生排班的混合整数数学规划模型，提出模型的线性化方法，并设计禁忌搜索算法对模型进行求解.所得模型方法不仅可以应用于急诊医疗服务系统，也可以应用于其他类似的存在回流客流的时变排队系统.

1 时变、带回流客流的排队服务系统队长计算

急诊服务系统是一个涉及到多个科室、人员、设备、床位的复杂排队网络，其基本服务流程如下.首先，患者到达时按照危重级别分诊，危急患者需立即送至抢救室抢救治疗；普通急症患者需至急诊科各科室等待区域候诊.由于实际运营中，普通急症患者占绝对多数，针对该部分患者，其就诊流程如图1所示.患者按照先到先服务的等待规则，等待医生的第1次问诊.经第1次问诊后，少数患者无需检查直接离开急诊科或被安排住院，多数患者需至检查科排队检查，检查后返回急诊科，与初次到达急诊患者形成混合队列等待.医生再次诊断后，患者经过治疗离开急诊科或被安排住院.急诊科的医生排班将直接影响患者等待队长等服务质量的关键性能指标，因此首先研究在给定医生排班的情况下，如何近似计算每个时段结束时医生处和检查台处的患者队长.其中，医生处的患者队长为初次到达患者与回诊患者数量之和.

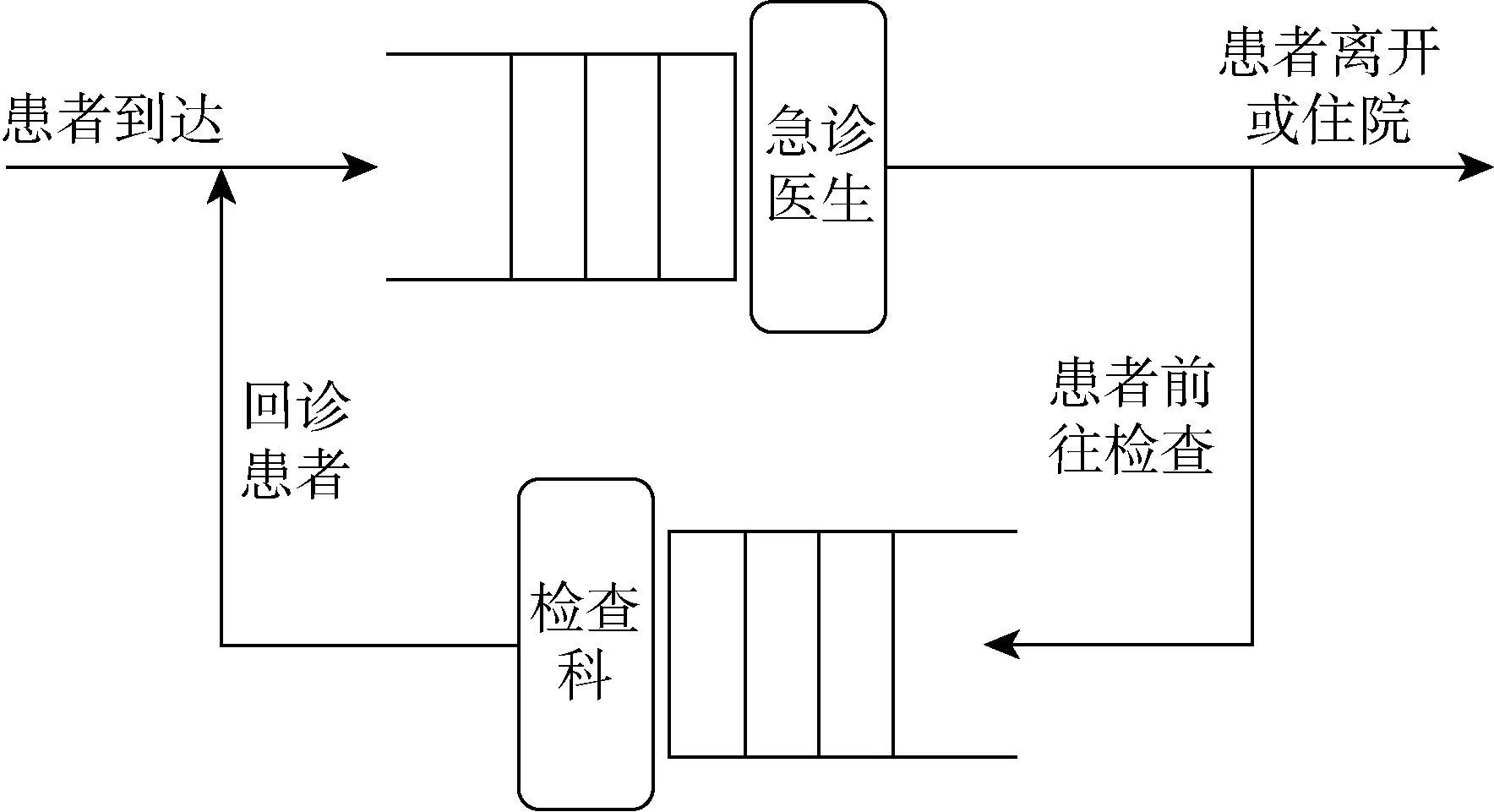
图1 急诊科室患者排队系统示意图Fig.1 Schematic diagram of queuing system of emergency patients

根据医院实际调研，做出以下设定：

(1) 研究聚焦一周的服务时间，其划分为若干等长时段，每个时段时长为δ，假设患者的平均到达率、医生数目在每个时段内均保持不变；

(2) 患者泊松到达，且不考虑未接受服务即离开的患者，第t个时段内患者到达率为λt；

(3) 医生及检查台服务对患者服务时间随机，均服从指数分布，设医生及检查台的服务速率不随时段变化，分别为μ1和μ2；

(4) 回诊患者排队时是否具有更高优先级并不影响医生处的队长结果，因此不妨设回诊患者在排队中无优先级.

1.1 不带回流的时变非稳态排队系统队长计算

由于带回流的时变非稳态排队系统的复杂性，首先探讨不带回流的时变排队系统队长计算方法，记该方法为“APP1”.基于以上设定，该系统为Mt/M/ct(时变泊松到达、指数分布服务时间、时变服务台数)的排队系统.对于第t个时段，排队系统时段初，系统中的顾客数加上时段内到达的顾客数应等于时段末系统中的顾客数加上时段内离开的顾客数.假设第t个时段内完成服务离开的顾客数为ut，时段初和时段末的系统队长分别为lt-1和lt，有如下流平衡方程成立：

lt+ut=lt-1+λtδ

(1)

Mt/M/ct排队系统流平衡模型如图2所示.

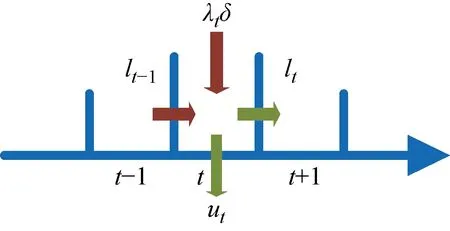
图2 Mt/M/ct排队系统流平衡模型Fig.2 Fluid balance model of Mt/M/ct queuing system

假设第t个时段的平均服务强度为ρt，单位服务台的服务速率为μ，则式(1)可改写为

lt+ctμρtδ=lt-1+λtδ

(2)

根据排队论，当系统中服务台数c>1，且服务强度ρ<1时，稳态M/M/c(泊松到达、指数分布服务时间、服务台数恒为c)排队系统中，顾客期望队长l的计算方法为[23]

(3)

(4)

需要指出的是，严格来说式(3)和(4)仅适用于稳态的排队系统，其中服务强度ρ是稳态M/M/c排队系统的服务强度.但是考虑到排队系统由于时变到达率无法达到稳态，所以采用一个时段内的短期平均服务强度ρt加以替代，即假设该时段排队系统处于稳态，且该短期平均服务强度的值为(ut/δ)/(ctμ).在该假设下，时段末系统队长lt可通过l(ρt,ct)近似计算.

由以上假设，lt为关于ρt和ct的函数，且当ct固定时，lt随ρt单调递增.将l(ρt,ct)作为lt代入式(2)，则式(2)仅有一个未知数ρt，且式(2)左侧关于ρt单调递增，右侧为固定值，显然满足式(2)的ρt存在且唯一，因此可以使用二分法快速迭代出ρt的近似值[24].经实验，一般经过20次迭代后即可使式(2)左右侧的绝对误差小于0.001.在获得ρt的近似值后，代入式(3)即可计算该时段结束时的系统队长lt.由于一个时段结束时的系统队长即是下一个时段开始时的系统队长，根据式(2)可求得每个时段结束时的系统队长.

本文考虑的排队系统在部分时段可能面临超负荷情况，即系统的服务能力小于顾客需求，尽管排队论中的服务强度λt/(ctμ)>1，但时段内的短期平均服务强度ρt的取值范围仍然在0～1，因此该方法仍然可用.当系统过负荷，即系统的服务能力远小于顾客需求(λt/(ctμ)>2)时，可以近似认为服务系统一直在以cμ的速率服务顾客，此时可将短期平均服务强度ρt近似取1，代入式(2)进行计算，即lt可通过下式计算(第t个时段的结束时队长不小于0)：

lt=max{lt-1+λtδ-ctμδ,0}

(5)

记式(5)所示的队长计算方法为“平稳流”方法.

1.2 带回流的时变非稳态排队系统队长计算

本节队长计算方法记为“APP2”.记医生和检查台分别为系统1和系统2，l1,t和l2,t分别为医生和检查台处在第t个时段结束时的队长.该时段的医生数和检查台数分别用c1和c2表示，医生处和检查台处的平均服务强度分别用ρ1和ρ2表示，假设顾客去往检查的概率为P.类似于Mt/M/ct排队系统，带回流客流的排队系统有流平衡等式如下：

l1,t+μ1c1ρ1δ=l1,t-1+λtδ+μ2c2ρ2δ

(6)

l2,t+μ2c2ρ2δ=l2,t-1+Pμ1c1ρ1δ

(7)

医生及检查台处流平衡模型如图3所示.对于l1,t和l2,t的计算同理，在c1和c2已知的情况下，式(6)和(7)仅有两个未知数ρ1和ρ2.对于一个给定的ρ2，代入式(6)使用二分法迭代可计算ρ1，再将迭代得出的ρ1作为给定值代入式(7)使用二分法迭代计算ρ2，重复以上求解过程直至式(6)和(7)左右侧绝对误差均足够小，再将ρ1和ρ2代入式(3)即可得到医生和检查台处的队长.

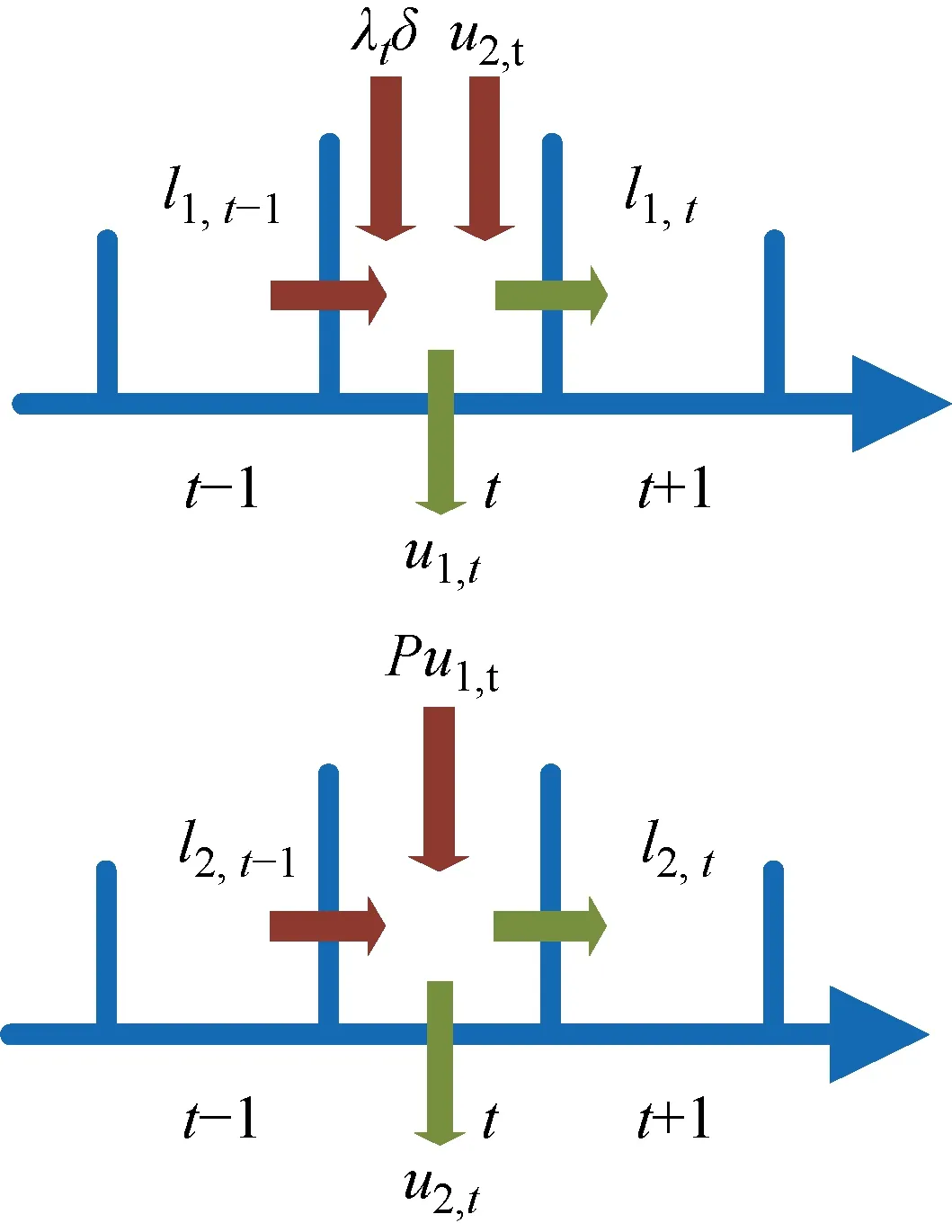
图3 医生及检查台处流平衡模型Fig.3 Fluid balance model of physicians and examination servers

同样地，当系统过负荷时，可将系统强度假设为1，代入式(6)和(7)计算医生和检查台处的队长.现实中一般医生处易处于过负荷状态(λt/(c1μ1)>2)，而检查台处往往不处于过负荷状态，在此种情况下可将ρ1假设为1，式(7)中仅有的未知数ρ2仍使用二分法迭代获得，ρ2代入式(3)获得检查台处的队长.医生处队长由下式计算：

l1,t=max{l1,t-1+λtδ+μ2c2ρ2δ-μ1c1ρ1δ,0}

(8)

2 医生周排班数学模型

基于以上队长计算方法，对急诊科室医生周排班问题建立数学模型.数学模型以最小化患者医生处总等待队长及医生人力成本为目标，确定每个医生一周的排班.在模型中，医生用集合K={1,2,…,O}表示，医生总数为O.排班周期为7 d，用集合A={1,2,…,7}表示，一周时间共168 h，分为168/δ个时段，用集合T={1,2，…,168/δ}表示.每天有N个相同的可用排班，假设N个排班中最后一个排班为夜班，所有排班用集合S={1,2，…, 7N}表示，第n个排班覆盖的时间范围用二元参数rn,t表示，该变量仅当第n个排班覆盖第t个时间段时取1，否则取0.c1,t为第t个时间段的医生数，检查台数c2设为常数.xi,n为二元决策变量，该变量仅在第i个医生被安排至第n个排班时取1，否则取0.由于系统队长的计算表达式非常复杂且非线性，无法直接使用求解软件如Gurobi直接求解，所以引入二元决策变量aj,t、bk,t、yl,t和dj,k,l,t对队长的计算线性化.假设U和V分别为l1,t和l2,t可能的最大取值，L1和L2分别为APP2近似中l1,t和l2,t的计算方法.医生周排班数学模型如下：

MIP1：

(9)

s.t.

(30)

式中：α为平衡系统队长和医生人力成本的系数；F为医生一周最大工作时长；G为医生两班最大时间间隔.目标函数式(9)为最小化患者的医生处总队长及人力成本；式(10)保证每个医生每天最多只在1个排班工作；式(11)保证医生上夜班后至少休息24 h；式(12)～(13)保证每个医生一周最多上夜班Cmax次，最少Cmin次；式(14)保证医生一周工作最多不超过Fh；式(15)给出每时段医生数；式(16)～(17)保证每时段医生数不超过最大医生数且不少于1；式(18)保证每个医生两班间隔不少于G；式(19)～(20)使只有在l1,t=j时，aj,t才取为1；式(21)～(22)使只有在l2,t=k时，bk,t才取为1；式(23)～(24)使只有在c1,t=l时，yl,t才取为1；式(25)～(26)使只有在l1,t=j、l2,t=k且c1,t=l时，dj,k,l,t才取为1；式(27)～(28)给出每时段结束时医生和检查台处队长；式(29)～(30)为初始化条件.尽管以上模型可以被离散线性化[1]，但由于以上问题规模很大且约束复杂，使用求解软件求解得到的解质量不高，具体见数值实验4.3节.

3 算法设计

由于使用求解软件(如CPLEX、Gurobi等)对以上模型求解非常困难，本文设计了一种禁忌搜索(TS)算法，基本流程如图4所示.其中：s为每轮迭代的当前解；s0为初始解；s′为领域中最好的可行解.

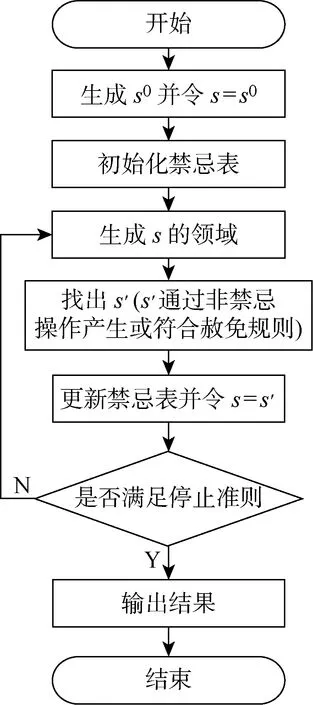
图4 禁忌搜索算法流程图Fig.4 Flowchart of TS algorithm

3.1 产生初始解

算法通过简单的原则产生初始可行解s0.首先，安排第i个医生(当医生数O≥7)值第md 的夜班(i=m, 1≤m≤7)，接着通过“First-accept”策略安排医生使每个时段都有医生上班，即当某时段医生数为0时，找到覆盖该时段的排班中序号最小的，将能够满足所有排班约束的最小序号的医生安排至该排班，重复这一过程直到每个时段医生数均大于0.通过以上过程能够得到医生上班总时长最小的初始解，在此解的基础上，将医生按贪婪法安排排班，即选择能最小化目标函数值的位置加入排班，直到每个医生均无法再加入更多排班.

3.2 邻域结构及禁忌操作

获得解s0后，记该解为第1个当前解s，构造当前解的邻域集合，邻域解通过以下两个操作产生：① 为1名医生增加1个工作班次；② 去除1名医生的1个已有排班.若解集合中所有解均为不可行解，则随机选择两个医生的两个排班交换，直到产生新的可行解作为新的当前解(实验中未出现由以上邻域操作产生的邻域集合全部为不可行解的情况).获得邻域集合后，选择集合中最好的一个邻域可行解s′，令其为新的当前解.为了防止算法在迭代过程中陷入局部最优，反复搜索已经搜索过的解或解空间，算法需要规定禁忌操作.算法的禁忌规则设计如下：若一轮迭代中当前解为s，产生新的当前解为s′，定义使解s变化至解s′操作的逆操作为该轮迭代的禁忌操作，并在此后θ轮迭代中禁止该禁忌操作.

3.3 解评估

算法需要对当前解的所有可行邻域解进行评估，即计算该解对应医生排班下的目标函数值，所提算法对患者等待队长的近似评估使用1.2节中“APP2”系统评估方法.

3.4 赦免规则

若当前解的一个邻域可行解通过被禁忌的操作产生，但其目标函数值较当前最好解的目标函数值更好，则算法对该解实行赦免，即取消对该解的禁忌限制.

3.5 停止条件

所设定算法的迭代次数为停止条件，当算法迭代给定次数(如500次)后停止并输出当前最好解.

4 数值实验

设计数值实验验证所提出的队长近似方法和TS算法.首先，针对医院实际的患者到达数据和医生排班方案，通过对比仿真结果验证所提出的队长近似方法的有效性，然后使用设计的TS算法对医院的医生排班进行优化，并将TS算法解分别与实际排班、基于仿真模型的遗传算法(GA)解和MIP1模型求解结果进行对比，以验证TS算法的有效性.数值实验所使用的硬件为3.1 GHz CPU，512 GB内存，运行Win10操作系统.

实验数据来自武汉市某医院急诊科5周的实际数据，该医院急诊科目前实际采用固定的四班制排班：8:00—16:00为第1班，9:00—17:00为第2班，17:00—1:00为第3班，1:00—9:00为第4班，每班分别安排1、2、1、2个医生.数值实验使用的柔性排班如表1所示，其他参数如表2所示.所有数值实验的系统初始队长均假设为0，流平衡允许误差设为10-4.

表1 柔性排班的班次时间Tab.1 Schedule time of flexible scheduling plan

表2 数值实验参数表Tab.2 Parameters of numerical experiments

4.1 队长计算方法精度实验

表3 仿真与APP1、APP2近似方法的医生处总队长比较

从表3可以看出，在5个算例下APP2近似方法得到的总队长结果与仿真结果均非常接近，而由于未考虑患者的回流现象，APP1近似方法得到的总队长结果与仿真结果相差较大.APP1近似方法所得结果与仿真结果的相对误差均高于80%;APP2近似方法所得结果与仿真结果的相对误差均低于5%，5个算例使用APP2近似方法得到的平均总队长为 1 586.24，而仿真结果为 1 627.96，平均误差为2.44%.由图5和6可以看出，APP1近似方法与仿真结果在每时段结束时的医生处队长上有明显差别，而APP2近似方法与仿真方法得到的结果不仅趋势一致，在数值上也十分接近.因此，所提队长近似方法能够作为TS算法中的解评估方法.

图5 W2每时段结束时APP1、APP2医生处队长与仿真结果比较Fig.5 Hourly patient queue lengths by APP1, APP2, and simulation in the physicians’ queue of W2

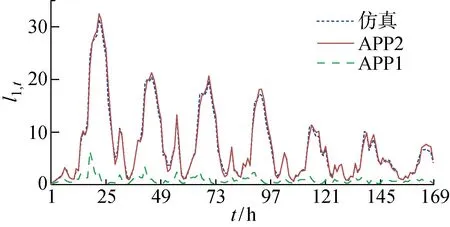
图6 W3每时段结束时APP1、APP2医生处队长与仿真结果比较Fig.6 Hourly patient queue lengths by APP1, APP2, and simulation in the physicians’ queue of W3

4.2 TS算法求解结果与实际排班方案的对比

使用所设计的TS算法对5个算例分别进行求解，设定算法迭代500次后停止并输出结果.每个算例的TS算法解与实际排班的目标函数值和患者医生处总等待时间如表4所示.其中：γTS为算法解；γREAL为实际排班值；tCT为算法求解时间；ω3为算法解与实际排班目标函数值的相对误差；ω4为算法解与实际排班患者在医生处的总等待时间的相对误差；tWT为患者在医生处的总等待时间，通过仿真得到.以W1为例，算法解与实际排班下的每时段结束时医生处仿真队长对比如图7所示，算法解与实际排班的对比如图8所示.

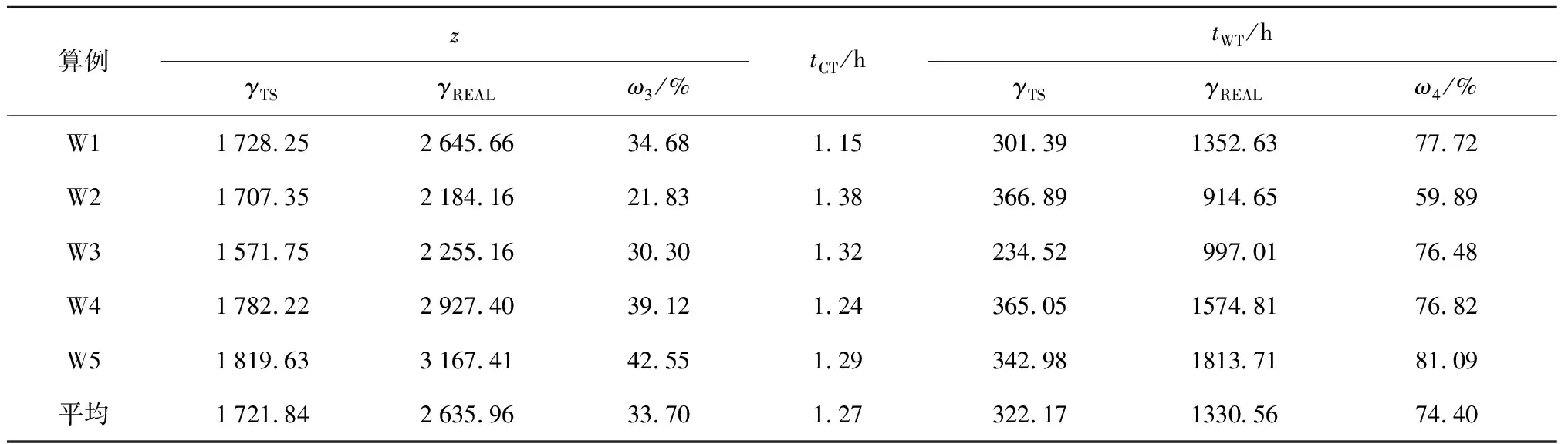
表4 TS算法解与实际排班对比Tab.4 Comparison of TS scheduling solutions and real scheduling plan

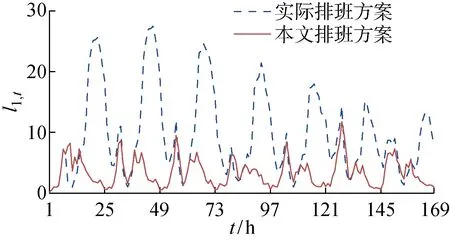
图7 W1时的TS算法解与实际排班下医生处仿真患者队长对比Fig.7 Comparison of patient queue lengths of TS scheduling solutions and real scheduling plan in the physicians’ queue of W1

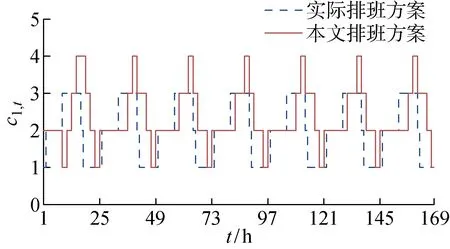
图8 W1时的TS算法解与实际排班各时段医生数对比Fig.8 Comparison of physician staffing plan of TS scheduling solutions and real scheduling plan of W1

由表4可以看出，每个算例的TS算法解对应的目标函数值较实际排班小21.8%～42.6%.同时，患者总等待时间的仿真结果显示，相比于实际排班，TS算法排班能够平均减少患者医生处的总等待时间70%以上.所有算例中，W2的算法运行时间最长，为1.38 h，5个算例的平均运行时间小于1.3 h.

由图7可以看出，TS算法排班能有效地降低患者的等待队长.相较于实际排班，算法排班下除了少量时段(如时段9～14、57～59、81～85)结束时的医生处队长较大，多数时段算法排班下的医生处队长更优，同时在算法排班下，医生处的峰值队长由27降至12，排队超过10人的“峰”的数量明显减少.对比W1患者的到达率变化和图8可以看出，使用表1所示的柔性排班方案，TS算法排班在患者到达的高峰时段(如15～18、39～40、63～64等时段)增加了医生数量以降低患者队长，而在患者到达率相对降低的时段(如9、34～35、57等时段)适当减少医生数量，从而在整体上减少患者在医生处的等待队长及等待时间.值得注意的是，表1所示的柔性排班方案并不适用于所有医院，医院可根据自身实际运营情况，设计并应用适合自身的柔性排班方案，降低患者的等待队长，提高医生的整体利用率.

4.3 与GA算法及大型优化软件结果对比

比较TS算法解与GA算法和MIP1模型的求解结果，以评估TS算法的有效性.首先设计GA算法，采用二进制编码方法，当第i个医生被安排至第n个排班时，第7iN+n位编码取1，否则取0.算法基本流程如下：首先对医生上班总时长最小的初始解编码，在此解的基础上随机改变1个基因位，生成50个个体组成初始种群，对编码解码后计算每个个体的适应度；在每一轮迭代中基于适应度采用轮盘赌方法对群体进行选择，对被选择的两个个体进行交叉，交叉方式为随机生成一个基因位，交换该基因位后的所有编码，交叉完成后对个体进行变异操作；随机选取1个基因位变异，交叉概率为0.8，变异概率为0.15；迭代500次后终止计算，将算法迭代中得到的具有最优适应度的个体作为算法的最好解输出.

与TS算法不同，GA算法对于待评估的个体采用基于仿真的方法计算其适应度(即目标函数值).首先，根据编码与医生排班的对应关系解码得到该个体对应的医生排班方案，再对该排班方案进行仿真，计算每时段结束时医生处的排队队长，进而得到该个体的适应度.仿真模型采用基于事件的仿真方法，使用C++实现仿真程序，对每周的算例运行5×104次取平均得到队长仿真结果.为了进一步对比TS算法，同时使用软件Gurobi 9.0.2对MIP1模型进行求解，设定求解时间为 8 h.

GA、MIP1以及TS算法的求解结果对比，如表5所示.其中：ω5为GA与TS算法解目标函数值的相对误差；ω6为MIP1模型求解结果与TS算法解目标函数值的相对误差.

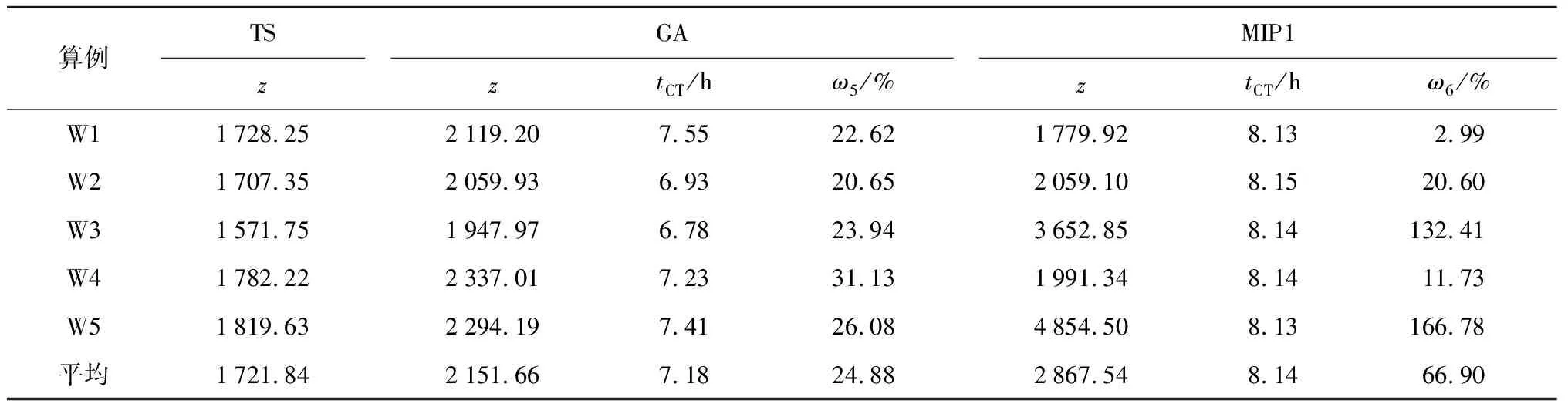
表5 TS、GA算法解与MIP1模型求解结果Tab.5 TS solutions, GA solutions, and solutions of MIP1 models

通过表5可以发现，TS算法解与GA算法解和MIP1结果的差异较为明显.TS算法解目标函数值较GA算法解平均小24.9%，较MIP1结果平均小66.9%，而TS算法的平均求解时间仅为GA算法和MIP1模型的1/5.同时，以计算时间为终止条件输出MIP1模型求解结果得到的解质量可能很差.通过以上对比可以发现，使用所提TS算法能够在合理时间范围内得到更好的医生排班方案.

4.4 算法参数分析和灵敏度分析

首先对TS算法的迭代次数进行分析，确定算法迭代次数的合理性，然后在W1数值实验的基础上，分别增加和减少医生数、医生最大工作时长、医生服务效率和检查台数，以对TS算法的表现进行灵敏度分析.以W1和W2为例，TS算法每轮迭代后最好解的更新如图9所示，其中：η为算法迭代次数.

图9 TS算法收敛速度Fig.9 Convergence rate of TS algorithm

由图9可以看出，在TS算法迭代过程中，最好解的目标函数值在前期迅速下降，并在迭代100次左右时基本达到收敛.尝试将迭代次数增加至 1 000，未发现更大的迭代次数能带来解的改进.考虑到算法的解质量和求解时间，500次迭代次数是一个合理的终止条件.

在实际的患者到达及医生配置下，所提数学模型和TS算法可以给出合理的医生排班，降低患者的等待队长.在W1数值实验的基础上，每次只改变一个参数生成不同的场景，研究TS算法的表现.在第1、2个场景中，可用医生数由原先的9分别增加至10和减少至8；在第3、4个场景中，每个医生的周最大工作时长分别增加和减少10%；在第5、6个场景中，医生的服务速率分别增加和减少10%；在第7、8个场景中，检查台数由原先的10分别增加至11和减少至9.由于医院实际排班无法更改医生数或医生工作时长，场景1～4使用如下方法产生新排班方案：在场景1、2中分别增加和减少1个医生，假设该医生每天在同一个班次工作；在场景3、4中分别给每个医生增加和减少1个工作班次，对每个场景均选择目标函数值最小的新排班方案.由仿真得到的8个新场景下TS算法排班和实际排班的目标函数值如表6所示.

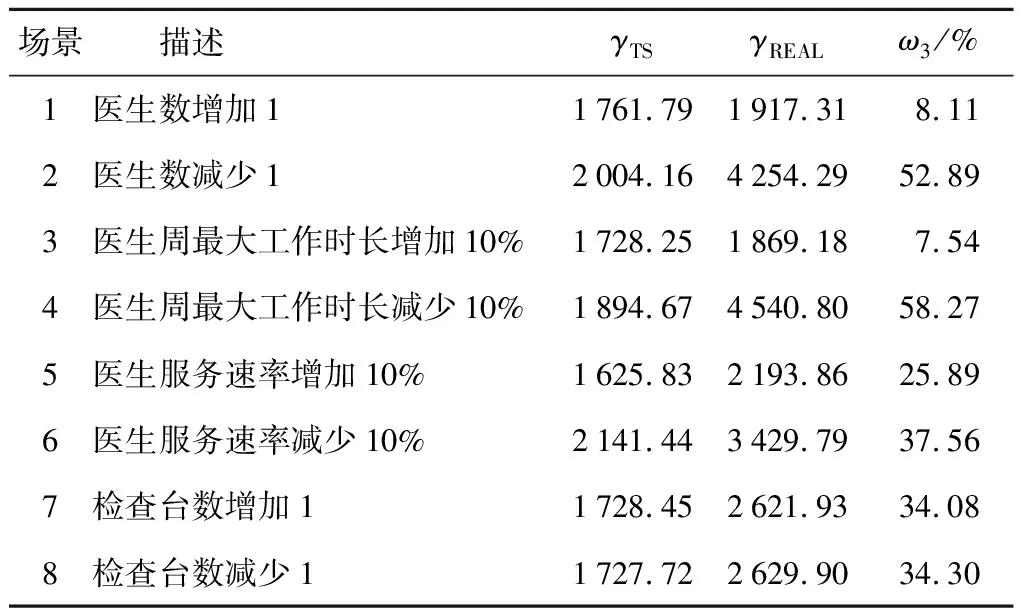
表6 不同场景下TS算法解与实际排班的目标函数值对比

从表6可以看出，在场景1～8下TS算法排班的目标函数值较实际排班小7.5%～58.3%.对比表4和6可以发现，即使可用医生数减少1或医生的周最大工作时长减少10%，TS算法排班的目标函数值仍优于医院实际排班的目标函数值(2 645.66).以上实验表明，所提 TS算法对不同场景均能给出合理的排班方案.

4.5 非负指数分布服务时间拓展实验

本文所提出的“APP2”队长近似计算方法建立在患者到达时间间隔和服务时间均服从指数分布假设基础上.医院实际运营数据显示，指数分布的患者到达时间间隔可作为实际情况的一种合理近似，而实际服务时间与指数分布则常偏离很大.因此，本文对比了TS算法排班与医生实际排班在非指数分布服务时间下的患者医生处总等待队长和总等待时间.医生和检查台的服务时间均服从退化分布和Erlang分布时患者医生处总等待队长和总等待时间分别如表7和8所示.其中：ω7为“算法解”与“实际排班”医生处总等待队长的相对误差；退化分布和Erlang分布的参数均经过调整，使医生和检查台的服务时间均值与表2所示的指数分布下的服务时间均值大小一致；Erlang分布的阶数取为3；患者医生处总等待队长和总等待时间结果均通过仿真得到.由表7和8可以看出，当服务时间不满足指数分布的情况下，TS算法排班仍能够有效降低患者的总等待队长和总等待时间.当医生和服务台的服务时间服从退化分布时，算法解相比实际排班，患者的总等待队长和总等待时间平均分别减少了63.7%和78.2%，当医生和服务台的服务时间服从3阶Erlang分布时，算法解相比实际排班，患者的总等待队长和总等待时间平均分别减少了63.0%和76.2%.

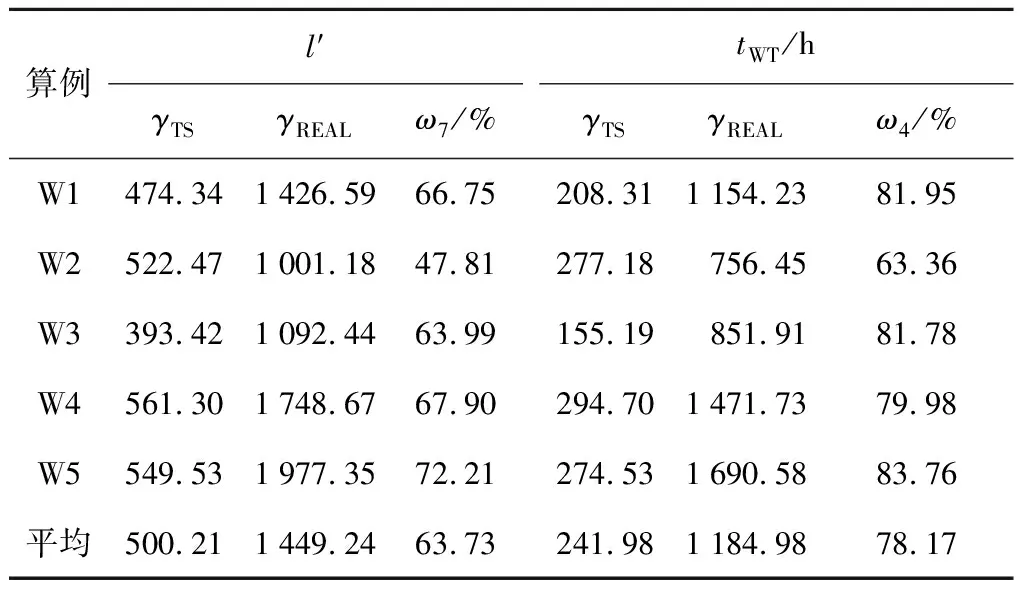
表7 退化分布服务时间下的TS算法解与实际排班对比

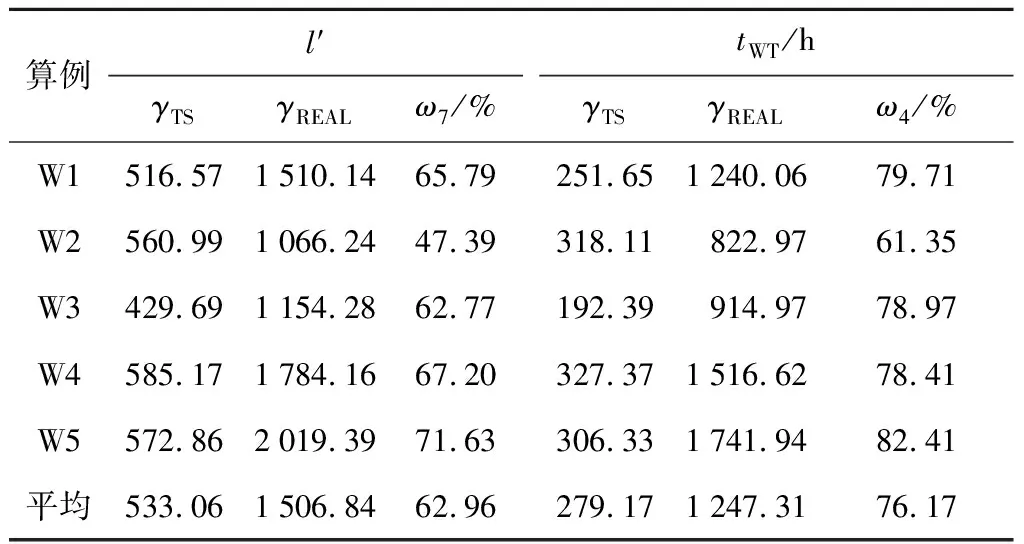
表8 Erlang分布服务时间下TS算法解与实际排班对比

5 结语

医院急诊科往往面临时变、回流的患者流，由于医院服务能力有限，急诊科常常面临拥挤，解决方法之一是将医生排班的传统排班方案改为柔性排班方案.为了得到较优的医生周排班方案，本文首先提出了一个时变、带回流客流排队服务系统的队长近似方法，该方法将排班周期分割为若干等长的时段，对每个时段建立流平衡方程并近似将每个时段内的系统视为稳态，应用稳态下的排队论公式和二分法，给出了每个时段结束时系统队长的近似值.基于该系统评估方法，针对急诊医疗排队服务系统建立了一个混合整数规划模型，并设计TS算法求解医生的周排班方案.基于武汉市某医院急诊科实际数据的数值实验显示，本文所提出的队长近似方法能够很好地近似时段结束时的系统队长，TS算法得到的优化排班能够有效地降低患者的等待队长，进而缓解急诊科的拥堵现象.

将所提出的模型扩展至更一般的排队网络，可以将其应用于更实际的场景.后续的研究可以从以下几个方面进行扩展：① 由于不同医疗检查所需时间不同，考虑在检查台处根据患者的检查类型分流，研究不同患者不同检查的排队网络；② 由于部分患者经医生检查后需要进入观察区，接受一段时间观察方能判断是否需要再次返回医生处问诊，考虑引入观察区，研究患者经观察后返回医生处再次问诊的排队网络.