重力异常向上延拓严密改化模型及向下延拓应用

黄谟涛，邓凯亮，吴太旗，欧阳永忠，陈 欣，刘 敏，王 许

1. 海军研究院，天津 300061； 2. 自然资源部海洋环境探测技术与应用重点实验室，广东 广州 510300； 3. 91001部队，北京 100830

依据地表重力观测研究确定地球形状大小及其变化特性，是重力和大地测量学的核心研究任务，既包含传统的大地测量边值问题解算和局部重力场逼近，又涵盖外部重力场逼近计算和全球重力场建模[1-5]。外部重力场逼近计算主要有两个方面的重要应用，一是为精密确定运载火箭、人造卫星、宇宙飞船、导弹武器、航天飞机等航天器飞行轨迹提供重力异常场补偿[6-7]；二是为近地空间开展重力测量数据质量评估提供比对基准[1,8-9]。重力异常向上延拓是外部重力场逼近计算最重要的研究内容之一，它既可直接用于地球外部重力异常计算，又可间接用于重力异常向下延拓迭代解算[2,10-14]。这说明互为反问题的重力异常向上和向下延拓不仅在计算地球物理学研究中发挥着不可替代的作用[15]，在大地测量边值问题“先向下后向上”解算中也具有非常重要的应用价值[1,2,16-17]。Poisson积分方程是计算地球外部重力异常的基础数学模型，它源于大地测量底律希勒(Dirichlet)边值问题的球面解，因其不能顾及地形高度的起伏变化，故在陆域实施重力异常向上延拓计算时，必须在Poisson积分模型基础上补偿地形效应的影响。早在1966年，Moritz就推出了一组依据地面重力异常和地形高数据计算外部重力异常严密而复杂的积分公式[10]。但由于受数据保障条件的限制，在实际应用中，人们更多采用的是所谓“移去-恢复”技术，即首先移去地形质量对观测重力异常的影响，然后使用Poisson积分完成向上延拓计算，最后在计算结果中恢复地形质量的影响[7,17]。显然，不管是采用顾及地形效应的严密公式，还是“移去-恢复”技术，都离不开Poisson积分方程的理论支撑和模型工程化实现。因此，精密求解Poisson积分方程自然就成为获取高精度重力异常向上延拓计算结果的核心关键。

计算地球外部重力异常的向上延拓公式是一类有代表性的全球积分模型，其积分核函数具有与三维空间Dirac函数相似的特性，当计算点由外部空间趋于数据观测界面时，积分计算会出现由Dirac核函数引起的数值跳跃现象；而当计算点趋于数据点或与数据点重合时，此类积分式还会出现不同程度的奇异性问题，需要通过引入合适的积分恒等式变换，将原计算模型转换为具有稳定数值解的连续函数模型[1]。其次是，受观测数据覆盖范围的限制，实施计算时需要对此类全球积分模型进行积分域分割处理，即将全球积分划分为近区和远区，近区采用实测重力数据进行数值积分计算，远区则采用地球位模型进行补偿[4]。需要指出的是，第一阶段为消除奇异积分而实施的积分恒等式变换通常是在全球积分意义下完成的，在第二阶段实施全球积分域分区处理时，人们往往会忽视积分恒等式成立的全球积分条件[1,18-19]，不再关注采用局域积分对积分恒等式带来的数值影响，从而引起不可忽略的计算模型误差[20]。为此，本文针对地面重力异常向上延拓全球积分模型改化问题进行分析研究，依据实际应用中的数据保障条件和全球积分域分割处理方式，推导出外部重力异常全球积分模型的严密改化公式，同时通过数值计算检验，分析验证采用严密改化模型的必要性和有效性。

1 计算模型改化与分析

1.1 重力异常向上延拓全球积分模型及稳定性分析

由重力位场理论得知，依据球外Dirichlet问题球面解的Poisson积分方程，可直接推得由地面观测重力异常计算地球外部重力异常的全球积分式为[1]

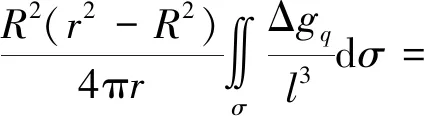
(1)

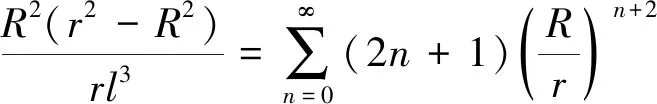
Pn(cosψ)

(2)

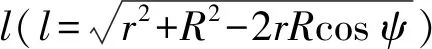
首先，将全球积分域σ划分为σ1和σ2两部分，σ1代表以计算点为中心、s1为半径且无限接近于计算点的小球冠区域，σ2代表剩余部分(σ-σ1)的区域。因当r→R，ψ≠0时，K(r,ψ)→0，故对应于σ2部分的积分项为零。可见，只需分析讨论对应于小球冠σ1部分的积分项。考虑到σ1是一个很小的区块，故可在该区块内对由式(2)表示的积分核函数作平面近似处理，以极坐标系(s,α)表示，可近似取

式中，h代表计算点的高度。此时，式(2)表示的积分核函数可近似表示为

(3)

将式(3)代入式(1)，得σ1部分的积分为

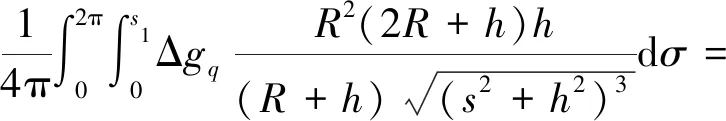
(4)

在无限小的球冠σ1内，可将Δgq看作一个常值，恒等于计算点处的重力异常，即可取Δgq=ΔgRp，代入式(4)，得

(5)

由式(5)看出，当h→0(即r→R)时，Δgpσ1→ΔgRp，即计算值收敛于地面上已知的重力异常观测值。很显然，这只是理论上的理想化推证结果，在实际应用中，是无法完全按照上述推证过程来实现重力异常向上延拓数值计算的。因为，选择一个无限小的球冠σ1既不现实也不符合数据实际，而当计算点与数据点重合时，在超低空高度段，由式(2)表示的积分核函数会出现非常严重的奇异性问题，从而导致式(1)的数值计算结果严重偏离预期的理论“真值”，这些都是由地球外部扰动位(类同于单层位)法向导数在边界面存在不连续性的固有特性和积分核函数具有与三维空间Dirac函数相似的跳跃特性所决定的[1]。尽管通过直接扣除计算点所在的数据块，理论上即可消除积分奇异性问题，但因该数据块距离计算点最近，对计算结果的影响也就最大，故扣除该数据块必然会对计算结果带来一定程度甚至是不可忽略的影响，从而显著降低向上延拓结果的计算精度[19]。

1.2 全球积分模型严密改化公式

为了消除式(1)的奇异性，确保地球外部重力位场调和函数在边界面上的连续性，Heiskanen和Moritz[1]建议采用由式(6)定义的积分恒等式对式(1)进行改化

(6)

在式(6)两端同乘以地面计算点处的已知观测值ΔgRp，可得

(7)

将式(1)减去式(7)，并略加整理可得

(8)

式(8)即为经去奇异性改化后的地球外部重力异常全球积分计算公式。不难看出，经积分恒等式(6)变换后，式(8)不再存在积分奇异性问题。同时，理论上，当r→R和ψ→0时，由式(8)确定的外部重力异常Δgp收敛于球面上已知的观测值ΔgRp。可见，经第一步改化后的计算式(8)在边界面也不再出现数值跳跃现象。至此，就从理论上解决了式(1)存在的积分奇异和数值不连续性问题。

如前所述，受观测数据覆盖范围的限制，在实际应用式(8)时，通常需要将全球积分域划分为近区和远区处理，近区定义为以计算点为中心、ψ0为半径的球冠区域σ0，通过引入一定阶次(比如N阶)的重力位模型参考场和移去恢复技术，在近区采用实测数据(减去N阶重力位模型)进行计算，远区效应则采用更高阶次(比如L阶)的重力位模型进行补偿。引入“移去-恢复”处理模式后，还需要对积分核函数作相应的改化处理，以满足积分核函数与观测重力异常信息之间的频谱匹配要求[21-22]。这里统一使用简单实用的Wong和Gore[23]方法对积分核函数进行改化。经分区处理和核函数改化后，式(8)从全球积分模型转换为局域积分模型，即得第2步改化公式

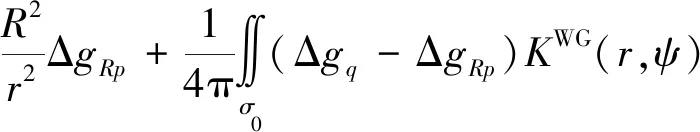
dσ+Δgq(σ-σ0)

(9)

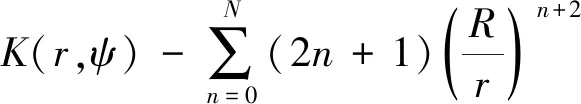
(10)

(11)

(12)

(13)

(14)

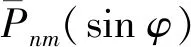
需要指出的是，当把式(9)作为计算外部重力异常的实用公式使用时，往往会忽略一个事实：式(8)是从积分恒等式(6)变换过来的，两者都建立在全球积分基础之上[1,19]。很显然，分区改化模型计算式(9)中的局域积分并不满足恒等式(6)的理论假设要求，因为Δgq(σ-σ0)只代表对式(9)右端积分项Δgq在远区(ψ0-π)的补偿，并未顾及另一积分项ΔgRp在远区(ψ0-π)的影响。这就意味着，一直在使用的重力异常向上延拓计算模型即式(9)是不严密的，存在系统性偏差。数值试验结果表明，由此引起的外部重力异常计算误差随观测值ΔgRp和积分半径ψ0取值大小变化而变化，最大可达数十mGal(mGal=10-5m/s2)。因此，要想获得高精度的外部重力异常计算结果，必须消除该项误差的影响。由前面的分析不难得知，该项误差的计算式可表示为

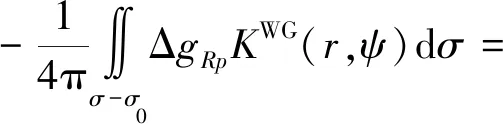
(15)

式中，Δgp(σ-σ0)代表ΔgRp在积分远区(σ-σ0)的影响。将式(10)代入式(15)，得

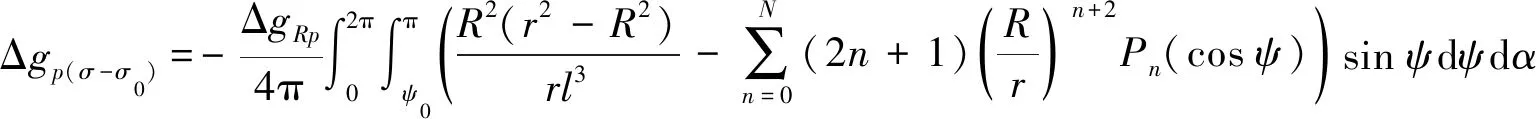
(16)

完成式(16)积分后可得

(17)

(18)

(19)

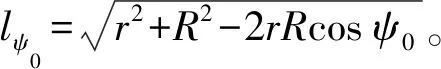
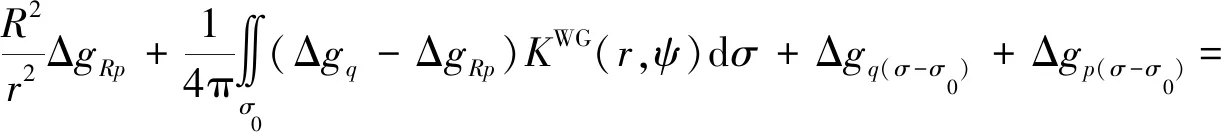
(20)

由式(8)推导过程得知，计算点所在数据块ΔgRp对计算参量Δgp的影响已经在式(8)右端的第一项中得到补偿，故在式(20)右端的积分项中不再体现数据块ΔgRp的作用。需要指出的是，这样的处理结果是在把数据块ΔgRp当成常值条件下获得的，如果该条件不满足，那么还应对数据块ΔgRp作单独处理。假设与计算点重合的网格数据块半径为ψ00，考虑到该数据块是一个很小的区域，故可采用与上一小节相同的方式对由式(2)表示的积分核函数作平面近似处理，此时，计算点所在数据块的积分式可写为

sdsdα

(21)

式中，Δgp0代表计算点所在数据块对计算参量Δgp的影响；s0代表数据网格大小的一半，当数据网格为1′×1′时，s0=0.5′。由式(21)得知，如果把数据块ΔgRp当成常值看待，即认为在计算点所在的数据网格内处处满足Δgq=ΔgRp，则有Δgp0=0。当计算点附近的重力异常场变化比较剧烈时，上述处理方法会带来一定的计算误差，此时，可参照文献[1]的思路，将重力异常Δgq在空间计算点P的球面投影点Rp处展开为泰勒级数

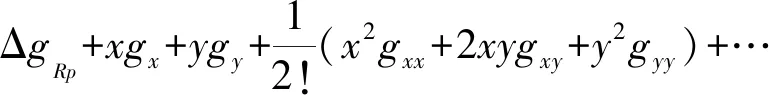
(22)

式中，x轴指向正北，y轴向东，x=scosα，y=ssinα。并且有

将式(22)代入(21)，可得

(23)

假设计算点所在的数据格网为(i,j)，则有

(24)

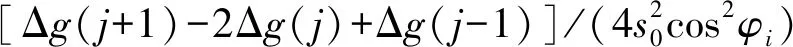
(25)

将式(23)代入式(20)的右端，可得到计算外部重力异常的第4步也是最终的严密改化公式

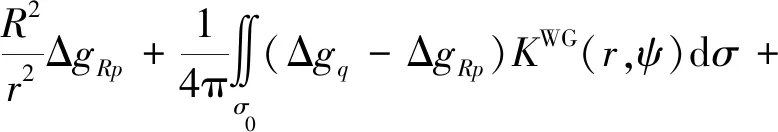
Δgq(σ-σ0)+Δgp(σ-σ0)+Δgp0

(26)

相比传统的向上延拓计算式(9)，式(26)增加了Δgp(σ-σ0)和Δgp0两个补偿量。

1.3 严密改化公式在向下延拓迭代计算中的应用

如前所述，位场向下延拓实为同一位场向上延拓的反问题，由于向上延拓解算具有稳定可靠的优良特性，因此在重力场向下延拓迭代计算中具有多方面的应用：①通过向下和向上延拓迭代计算将航空重力测量成果向下延拓到某个基准面[10,22,25-26]；②将地面观测重力异常向下延拓到地球内部的某个球面，然后采用球面延拓公式完成向上延拓计算[10,17]；③将地面或航空重力测量成果统一向下延拓到大地水准面，用于解算大地测量边值问题[1,27]；④将地面或航空重力测量成果向下延拓到地球内部更接近于位场源体的高度面，以提高位场数据解释推断的准确性和可靠性[15,28-29]。在这些应用中，重力异常向上延拓模型几乎都是以同一个方式为各方所用，也就是在向下与向上的迭代计算中起到一个关键性的桥梁作用。以航空重力测量数据向下延拓计算为例，具体原理和流程说明如下。

假设在高度为h的等高面上完成了航空重力测量，经处理后得到一组重力异常网格值Δgp，现需要将Δgp向下延拓到半径为R的球面上。由式(26)得知，现在的问题是已知向上延拓方程左端的球面外部观测量Δgp，需要求解方程右端第一项和第二积分项内的球面重力异常ΔgRp

(27)

由式(27)还不能直接求得球面值ΔgRp，因为式(27)右端仍包含未知参量ΔgRp和Δgq。为了解决此问题，一般采用迭代计算方法对式(27)进行求解。首先取迭代计算初值

(28)

(29)

(30)

如此继续进行，按式(31)计算ΔgRp第k次近似值

(31)

直到前后两次计算值的互差绝对值或互差均方根值小于某个设定的大于零的限差值ε或σ(如可取ε=0.3 mGal或σ=0.1 mGal)为止。

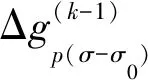
2 数值计算检验与分析

2.1 数值检验使用的数据及区域

为了分析比较前面提出的重力异常向上延拓积分模型改化效果，本文采用超高阶位模型EGM2008作为数值计算检验的仿真标准场[31]，用于模拟产生球面及其外部设定高度的1′×1′网格重力异常理论“真值”(这里使用1′×1′而非5′×5′网格数据是为了减弱积分离散化误差的影响)。由地球位模型计算球面及其外部设定高度面重力异常的公式为[1,4]

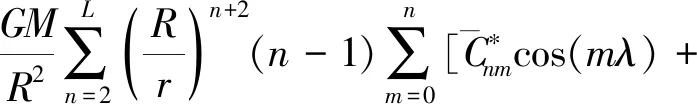
(32)

式中，各个符号的意义同前。

为了体现检验结果的代表性，这里特意选取重力异常场变化比较剧烈的马里亚纳海沟作为试验区，具体覆盖范围为：6°×6°(φ：10°N～16°N；λ:142°E～148°E)。首先选取截断到360阶次的位模型EGM2008作为参考场，即取N=360，然后选取361～2160阶次的位模型EGM2008作为计算检验的标准场，即取L=2160，进而选取ri=R+hi，R=6371 km，使用EGM2008模型(361～2160阶次)分别计算对应于9个高度面上的1′×1′网格重力异常理论“真值”Δgti(i=1,2，…，9),每一个高度面对应360×360=129 600个网格点数据，9个高度分别为：hi=0、0.1、0.3、1、3、5、10、30、50 km。表1列出了其中的5个高度面上的重力异常理论“真值”统计结果，图1、图2分别给出了对应于0 km高度面和3 km高度面上的理论“真值”分布态势图。表1为由EGM2008模型(361～2160阶次)计算得到的重力异常统计结果。

图1 0 km高度面重力异常分布Fig.1 The gravity anomalies on 0 km altitude surface

图2 3 km高度面重力异常分布Fig.2 The gravity anomalies on 3 km altitude surface

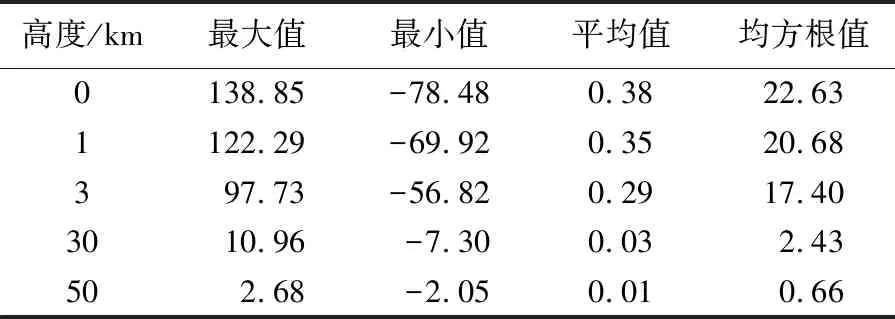
表1 由EGM2008模型(361～2160阶次)计算得到的重力异常统计结果

表1统计结果和图1、图2显示的重力异常变化形态说明，尽管已经扣除掉2～360阶次频段的参考场，本试验区域重力异常场变化的激烈程度仍然非常显著，足以代表真实地球绝大多数局部重力场的变化特征。

2.2 改化模型数值检验方法及结果分析

为了对比分析不同改化模型的计算效果，这里采用零高度面也就是球面上的1′×1′网格重力异常“真值”Δgt作为观测量，同时使用4种改化模型对前面选定的对应于试验区9个高度面上的1′×1′网格重力异常进行了计算分析。其中，第1模型是指直接使用式(1)作为基础计算模型，并对全球积分域作了分区处理，但在实施近区计算时，直接扣除掉与计算点重合的1′×1′数据块，以避免出现奇异积分；第2模型对应于式(9)；第3模型对应于式(20)；第4模型对应于式(26)。将4种模型的计算值分别与相对应的理论“真值”Δgti做比较，可获得不同改化模型的计算精度评估信息，具体比对结果列于表2。这里积分半径统一取为ψ0=2°，为了减小积分边缘效应对评估结果的影响，表2只列出试验中心区2°×2°方块内的数据比对结果(下同)。为了定量评估重力异常远区效应大小及由全球积分过渡到局域积分引起的模型误差影响，表3给出了采用式(11)计算得到的3组对应于积分半径ψ0=2°、ψ0=5°和ψ0=10°的远区效应贡献量Δgq(σ-σ0)统计结果，表4给出了采用式(17)计算得到的相对应的3组误差补偿量Δgp(σ-σ0)统计结果。表5为依据式(18)计算得到的比例系数k(r,ψ0,N)随位模型参考场阶数N、积分半径ψ0和高度h取值变化而变化的数值结果。

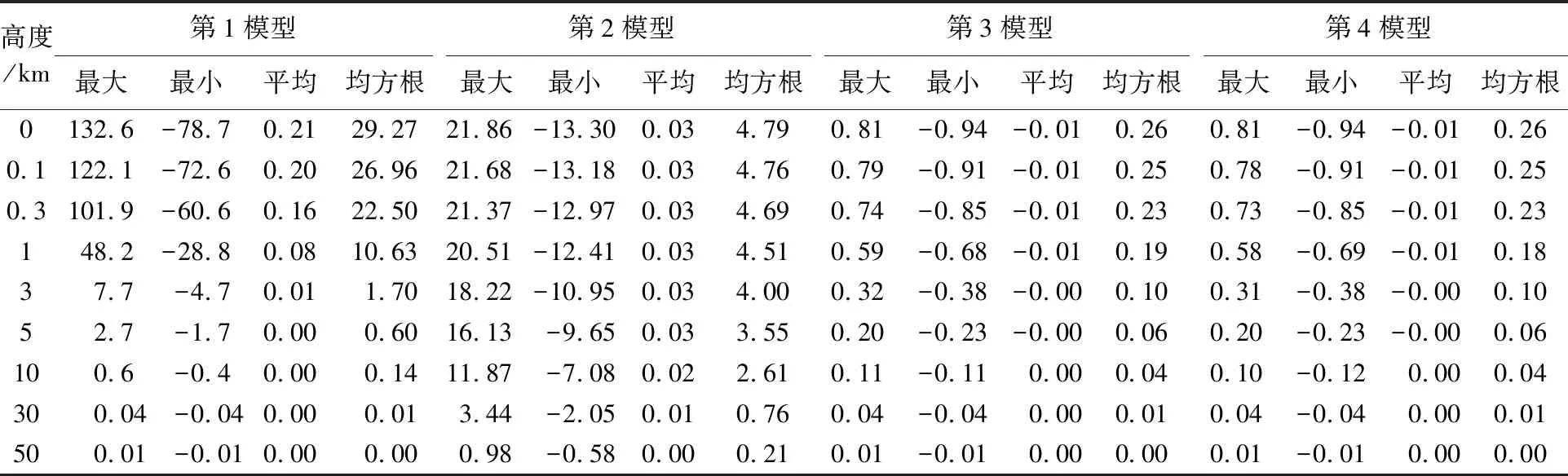
表2 由不同改化模型计算得到的9个高度面重力异常与“真值”比较Tab.2 Comparisons between the gravity anomalies from different modified models and the “true values” on 9 altitude surfaces mGal

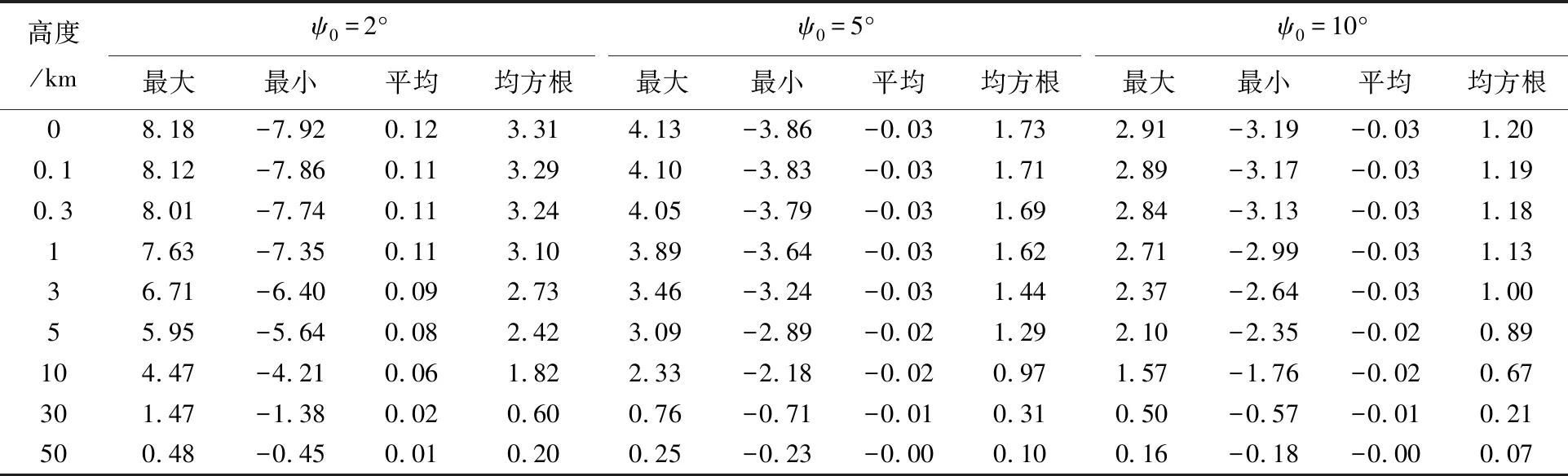
表3 远区效应贡献量Δgq(σ-σ0)结果统计Tab.3 Statistics of the computational results of far-zone contribution Δgq(σ-σ0) mGal

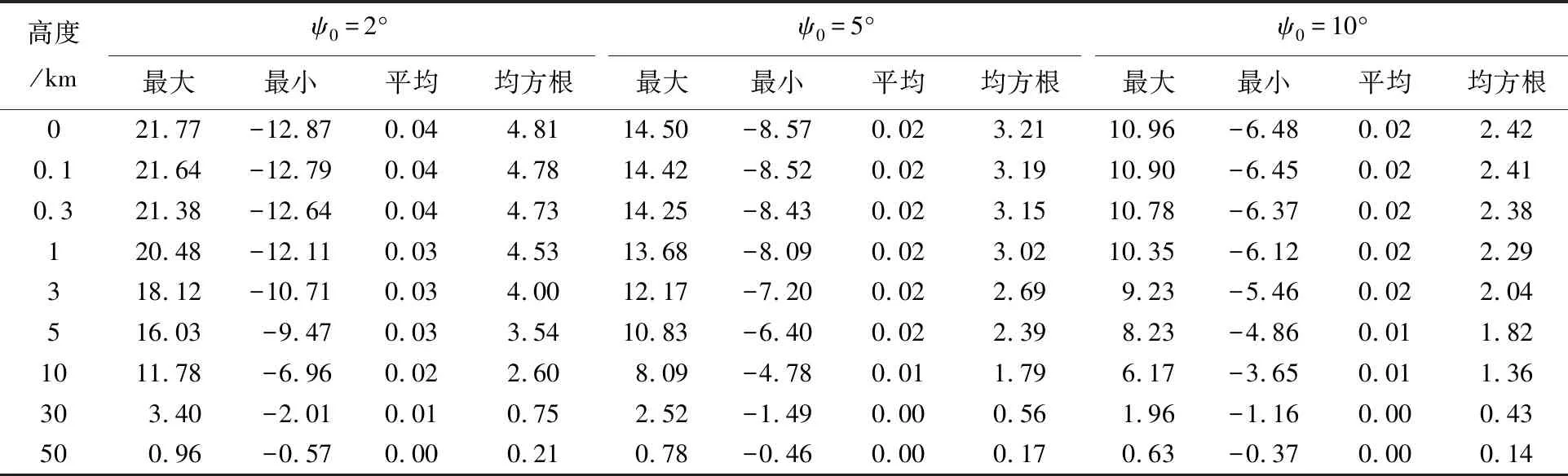
表4 模型误差补偿量Δgp(σ-σ0)计算结果统计Tab.4 Statistics of the computational results of error compensationΔgp(σ-σ0) mGal

表5 比例系数k(r,ψ0,N)随位场阶数N、积分半径ψ0和高度h变化情况Tab.5 The scale factor k(r,ψ0,N) with the changes of degree N, integral radius ψ0 and altitude h

由表2比对结果可以看出，除了第3和第4模型之间的计算结果差异较小以外，其他3个模型的计算精度差异明显。第1模型一方面由于直接扣除了计算点所在数据块的影响，另一方面在边界面附近，受数值积分不连续性影响严重，故在3 km以下高度段，该模型的计算误差起伏较大，从近30 mGal减小到不到2 mGal,变化幅度超过一个数量级，可见该模型不能直接用于这个高度段的重力异常向上延拓计算；第2模型尽管从理论上消除了核函数奇异性影响，并在超低空高度段取得了比第1模型好得多的计算精度，但由于该模型的改化过程存在不可忽略的缺陷，故即使到了10 km高度，该模型的计算误差仍然超过不可接受的2 mGal；第3模型从理论上弥补了第2模型的缺陷，使得该模型的计算精度得到显著改善，即使在零高度面，该模型计算值与比对基准“真值”的最大互差也不超过1 mGal，互差均方根值不超过0.3 mGal。这个结果说明，对第2模型所作的补偿改化处理是正确有效的，对于高精度要求的向上延拓计算应用，更是必不可少。第4模型是对第3模型的进一步改进和优化，理论上更加严密，其计算精度的改善幅度取决于采用的数据网格间距大小和计算点周围重力异常场变化的剧烈程度。理论上，采用的数据网格间距越大，计算点周围重力异常场变化越剧烈，第4模型相对第3模型的精度改善效果会越显著。本试验未能体现该模型相对于第3模型的显著改善效果，是因为这里采用的是1′×1′网格数据，而且是来自2160阶次的位模型EGM2008仿真数据，对应的1′×1′网格范围内的重力异常变化幅度相对较小。可以预见，如果是在重力异常场变化更为剧烈的大山区且使用更大网格(如2′×2′或5′×5′)的实测数据，那么第4模型定会显现出符合预期的优势。

由表3和表4计算结果可看出，重力异常远区效应贡献量和计算模型误差补偿量的大小均在毫伽级以上且后者大于前者，两者的影响都不可忽略。由表4和表5结果可进一步看出，尽管第3模型对第2模型的补偿量均随位场阶数N、积分半径ψ0和计算高度h的增大而减小，但当位场阶数取为N=360时，即使积分半径增大到ψ0=10°，计算高度h=10 km处的误差补偿量仍然超过1 mGal；而当积分半径取为ψ0=2°时，即使位场阶数提高到N=2160，高度h=1 km处的误差补偿量也可能超过1 mGal。这样的结果再次说明，本文对传统向上延拓计算模型进行精细改化是必要且有效的。

前面完成的数值计算检验都是基于输入数据无误差假设条件，得到的比对评估结果只是计算模型自身完备程度的反映。为了考察数据观测误差对向上延拓解算结果的影响，本文在前述试验基础上，进一步开展有输入数据误差影响条件下的数值计算检验。具体做法是，在前面作为观测量的位模型剩余重力异常“真值”Δgt中分别加入1 mGal和3 mGal的随机噪声，形成两组新的模拟观测量，然后按照前面相同的计算方案和流程，依次采用4种改化模型完成9个高度面上的1′×1′网格重力异常计算，最后将计算结果与相对应高度的重力异常“真值”做比对评估(表6、表7)。

将表6和表7的计算结果与表2作对比可知，数据误差对4种改化模型解算结果的影响规律是一致的，没有因为模型改化形式的不同而产生实质性差异，总体而言，数据误差只对5 km高度以下的计算结果产生有限度的影响。模型误差和数据误差共同作用于向上延拓解算结果，完全符合随机误差作用传播规律。不同的是，模型误差影响在第1和第2模型中占主导地位，相反，在第3和第4模型中，占主导作用的则是数据误差的影响。同时，相比较而言，在相同误差影响条件下，第4模型的计算效果要略优于第3模型。这些结果说明，即使采用严密的第3和第4改化模型进行重力向上延拓计算，也要尽可能将数据观测误差控制在较低的水平。

表6 1 mGal误差影响下不同改化模型计算得到的9个高度面重力异常与“真值”比较Tab.6 Comparisons between the gravity anomalies from different models with 1 mGal error and the “true values” on 9 altitude surfaces mGal

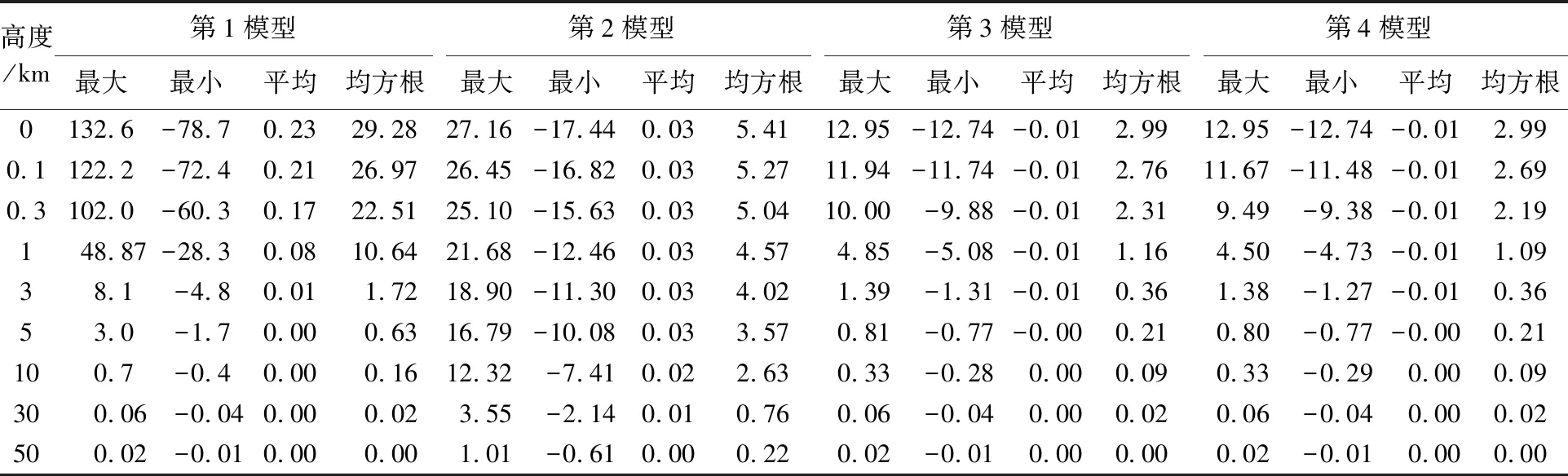
表7 3 mGal误差影响下不同改化模型计算得到的9个高度面重力异常与“真值”比较Tab.7 Comparisons between the gravity anomalies from different models with 3 mGal error and the “true values” on 9 altitude surfaces mGal

2.3 改化模型应用于向下延拓迭代计算效果检验

为了进一步检验前述严密改化公式应用于向下延拓迭代计算的实际效果，这里继续采用前面定义的4种向上延拓改化模型作为向下延拓迭代逼近的计算式，将事先计算得到的3 km高度面上的1′×1′网格重力异常理论“真值”向下延拓到0 km高度面，具体迭代过程见式(28)—式(31)。将由4种改化模型用于向下延拓迭代计算获得的重力异常网格值分别与0 km高度面上的理论“真值”做比较，可获得相对应改化模型的应用效果评估信息，具体比对评估结果列于表8。为了比较，表8同时列出了输入数据存在观测噪声情况下的迭代计算比对结果。这里的积分半径同样统一取为ψ0=2°，结束迭代计算的阈值取为σ=0.1 mGal。表8所列结果只限于中心区2°×2°方块内的比对数据。

表8比对结果全面反映了向上延拓模型完备性对向下延拓迭代解算精度和稳定性的影响。首先，由表2检核评估统计结果得知，第1模型在3 km高度面的计算精度为1.7 mGal，第2模型为4.0 mGal，第3和第4模型均为0.1 mGal。表8比对结果说明，向上延拓计算模型误差越大，对向下延拓解算结果的影响也越大，需要迭代计算的次数也越多，模型误差和数据误差共同作用的结果也符合前面所作的理论分析预期。但观察迭代计算收敛过程可知，尽管随着迭代次数的增加，第1和第2模型的迭代解算结果也在缓慢逼近空中的观测重力异常，但向下延拓结果并不趋近于0 km高度面上的理论计算“真值”，表8中对应于第1和第2模型迭代结束后的比对结果并不是它们的最好结果。实际情况是，第1模型的最好比对结果出现在第2次迭代结束之后，第2模型出现在第1次迭代之后，具体比对结果列于表9。第1模型从第3次、第2模型从第2次迭代开始，随着迭代次数的增加，其相对应的向下延拓解算结果实际上是越来越偏离理论计算“真值”。显然，两个模型出现最好比对结果的迭代次数是无法预估的，与计算模型误差大小有关，具有较大的不确定性。模型误差较小的第3和第4模型则不存在这方面的问题。这样的结果再次说明，向上延拓计算模型完备程度直接决定向下延拓迭代计算精度水平，同时影响迭代计算结果的稳定性。

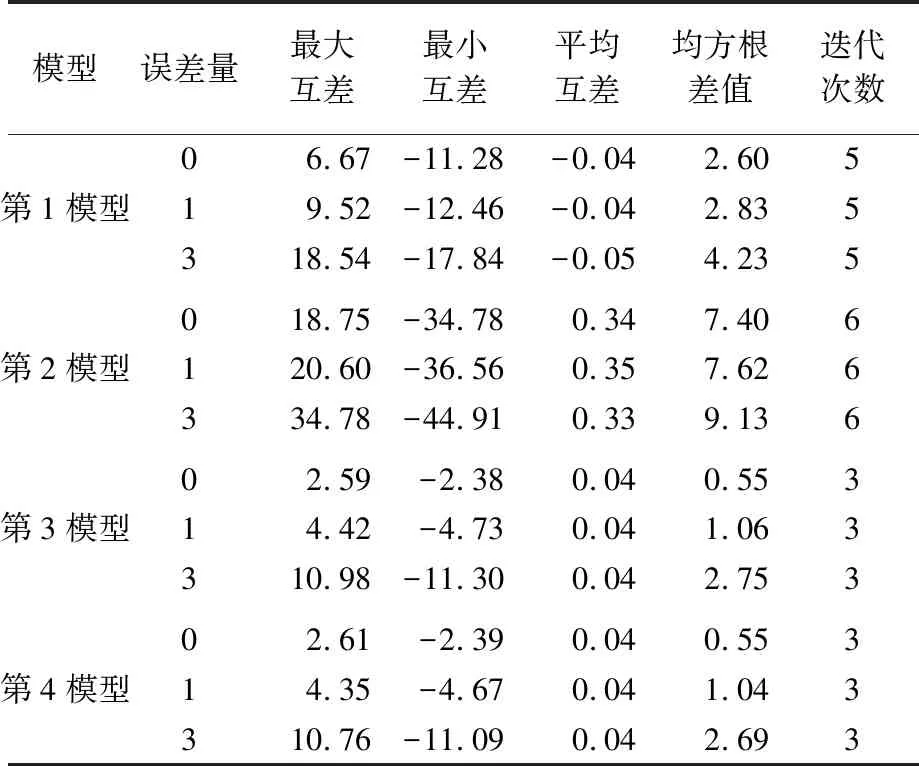
表8 有无误差影响下使用不同向上延拓改化模型进行向下延拓迭代计算结果与“真值”比较

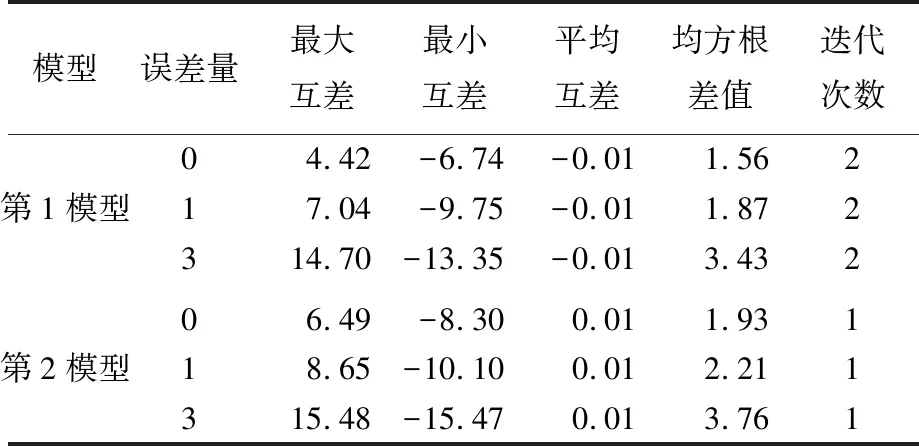
表9 有无误差影响下使用第1和第2向上延拓改化模型进行向下延拓迭代计算结果与“真值”比较

3 结 论

针对位场转换中经常遇见的重力异常向上延拓计算模型改化问题，本文分析研究了此类全球积分模型改化的技术流程和适用条件，指出了传统改化方法存在的理论缺陷，同时依据实测数据保障条件和积分恒等式适用条件要求，导出了重力异常向上延拓积分模型的分步改化公式，提出了补偿传统改化模型缺陷的修正公式。针对应用广泛的位场逆转换需求，提出了将最终的向上延拓严密改化模型应用于重力异常向下延拓迭代解算的方法和步骤。采用超高阶地球位模型EGM2008作为比对标准位场，同时选择在重力异常场变化比较剧烈的马里亚纳海沟区块开展数值计算符合度检验，分别对重力异常向上延拓分步改化模型的计算精度及在向下延拓迭代解算中的应用效果进行了检核分析和评估，表明采用严密改化模型是必要和有效的，不仅可显著提高重力异常向上延拓的计算精度，同时有利于提高向下延拓迭代解算过程的稳定性和可靠性。