非完整约束的OD/SINS自适应组合导航方法

刘万科，农 旗，陶贤露，朱 锋，胡 捷

1. 武汉大学测绘学院, 湖北 武汉 430079; 2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079

在地面车辆组合导航中，基于微机电系统(micro-electro-mechanical system，MEMS)技术的低成本惯性测量单元(inertial measurement unit，IMU)因其体积小、成本低而受到广泛应用，但受限于其误差发散快而无法单独使用[1-4]。全球导航卫星系统(global navigation satellite system，GNSS)已经被广泛应用于减少MEMS捷联惯性导航系统(strap-down inertial navigation system，SINS)误差累积，但当车辆在高楼之间、树荫和隧道内行驶时，GNSS会遇到频繁的信号遮挡甚至中断，导致组合导航结果发散[5-7]。

针对GNSS信号中断导致车辆组合导航结果发散的问题，国内外学者开展了一系列的研究工作。根据运动学原理，车辆在地面上运动时，如果没有侧向滑动或上下跳跃波动，其横向和垂直分量的速度将接近于零[1，8]，即车辆运动的非完整性约束(non-holonomic constraint，NHC)，因此可以在组合导航中构建虚拟的速度观测量。相关研究已经表明，里程计和NHC可以显著提高组合导航精度，增强SINS的性能，尤其是当GNSS信号不可用时，可以有效抑制组合导航系统的误差发散[9-13]。此外，有学者指出在使用NHC时，前向杆臂对非完整性约束的影响最大，为保证非完整约束辅助的准确性和可靠性，杆臂误差应控制在厘米级[14]。

NHC的虚拟观测信息是在特定的车辆运动状态中建立的，然而车辆在实际行驶时不可能完全沿直线，在转弯过程和速度较高的情况下，发生侧滑及垂向跳动是非常普遍的。因此，在使用NHC时应考虑车辆运动状态信息[15-18]，实时调整约束噪声。已有学者对车辆运动状态进行了相关研究，通过车辆速度与IMU的原始数据可以检测出车辆行驶过程中绝大部分转弯、小弧段变化及变道情况[18-19]，该方法为NHC自适应调整噪声提供了可能性，但相关学者没有进一步将NHC与车辆运动状态结合进行研究。

综上所述，目前学者们广泛将NHC用于抑制GNSS信号中断期间组合导航的误差发散，但大多数研究使用NHC时并未考虑车辆转弯等特殊情况，也未详细说明使用NHC时的噪声设置。为解决NHC固定噪声与车辆实际运动状态不相符的问题，本文分析了NHC噪声与车辆运动状态的关系，构建了一种基于车辆速度与运动状态的NHC噪声自适应估计方法，该方法通过IMU测量值与车辆CAN总线提供的速度测量值判断车辆运动状态，实现了NHC噪声的自适应估计。通过实测车载数据的分析表明，该方法能够较好地抑制GNSS中断期间组合导航系统的误差发散。

1 NHC/OD/SINS组合模型

1.1 状态方程

本文采用地心地固系(e系)松组合模型，系统状态选取机械编排结果的3轴位置误差δre、速度误差δve、失准角误差φ，IMU 3轴加速计零偏ab，3轴陀螺零偏εb，共15维

(1)

e系下机械编排误差的时域微分方程可表示为[20-21]

(2)

(3)

式中，ηa和ηε为随机白噪声。

将式(2)的时域微分方程离散化，可得到状态方程

Xk,k-1=Φk,k-1Xk-1+Wk-1

(4)

式中，Xk,k-1和Xk-1为当前时刻状态预测值和上一时刻状态值；Φk,k-1为状态转移矩阵；Wk-1为状态噪声。

1.2 观测方程

在车辆导航中，通常假设侧向与高程方向的运动速度近似为0，且NHC一般适用于非转向轮(即车辆后轮)。此外，从车辆的CAN总线中可以获取到前进方向的运动速度，即里程计(OD)速度vod。结合NHC适用于非转向轮，本文选取的b系的方向为右前上，即y轴朝车辆前进方向，x轴垂直于y轴朝车辆前进方向的右向，z轴垂直朝上。将NHC/OD组合，考虑IMU安装失准角为可忽略的小角度，可得b系下车辆的速度为

(5)

由惯性导航机械编排获得速度在b系下可表示为

(6)

其中，上标“～”表示该量带有误差(由机械编排直接获得)；“φ×”表示φ的反对称矩阵。

(7)

考虑NHC/OD测量值带有误差σ，则有

(8)

对式(8)进行扰动分析，即将机械编排的速度与理论真实速度相减，有

(9)

将式(7)代入式(9)，并整理得

(10)

式(10)即NHC/OD/SINS测量方程，可表示为

Zk=HkXk+σ

(11)

其观测噪声表示为

(12)

式中，σod为里程计测速噪声项；σNHC,x、σNHC,z为NHC噪声项，其值的大小反映了速度约束的松紧。

1.3 误差校正

滤波更新完成以后，立即进行全闭环校正操作，分为3步。

(1) 用公共误差状态修正机械编排结果，输出最终的导航参数，并且用该导航参数初始化下一历元机械编排中的位置、速度和姿态

(13)

式中，下标“mech”表示惯导机械编排结果。

(2) 用IMU误差状态修正下一历元的惯导输出

(14)

式中，Δvk+1、Δθk+1分别表示下一历元的加速度计与陀螺测量值；上标“^”表示该量进行了修正。

(3) 将所有误差状态置零

Xk=0

(15)

1.4 车辆转弯运动分析

对车辆转弯时进行运动学分析，如图1所示，A、B两点分别为前轴中心与后轴中心。根据阿克曼理论转向特性，车辆在转弯时所有车轮应绕着同一点O′做瞬时圆周转动，且点O′位于两后轮轴线延长线上，此时根据圆周运动原理，车辆后轴速度的方向应垂直于O′B(即沿vB1方向)。然而，阿克曼理论转向特性,是以汽车车辆前轮定位角都等于零、行走系统为刚性、车辆行驶过程中无侧向力为假设条件的，实际车辆的垂直载荷，轮胎结构、材料和充气压力，路面的形状及潮湿程度，侧向风，车轮外倾角，转弯半径和转弯速度等均会影响轮胎侧偏角，导致理论上瞬时转动点(O′)与实际瞬时转动点(O)无法交汇于一点[22-24]，即实际车辆转弯时是以O点为圆心做瞬时圆周转动。此时B点处速度vB的方向如图1所示，垂直于OB。对vB进行速度分解可得vB1与vB2，vB2为由于车辆转弯运动时产生横向速度分量。如上所述，其方向与车辆转弯幅值大小等因素相关。

图1 车辆转弯Fig.1 Vehicle turning

由以上分析可知，由于车辆轮胎的侧偏角等受转弯速度、转弯幅值等因素的影响，车辆在转弯时会产生一定的横向速度噪声，因此在设置NHC噪声时，不能设置为固定值，应当考虑车辆的运动状态进行自适应调整。

2 NHC噪声自适应模型

为研究NHC横向速度噪声与车辆运动状态的关系，选取了实际路测数据进行分析：数据于2020年8月27日下午在武汉市卓刀泉立交采集，轨迹如图2所示，标记点为主要的转弯的路段。试验使用加拿大NovAtel公司的PwrPak7测量型GNSS接收机与SPAN-FSAS高精度组合导航系统，通过Inertial Explorer 8.70软件后处理计算得到b系下车辆的行驶速度(vy)、右向速度(vx)及历元间航向角差(da)。

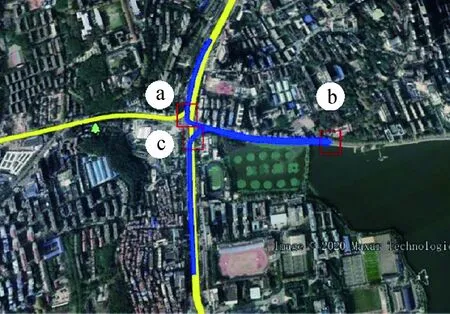
图2 路测轨迹(卓刀泉立交)Fig.2 Road test track (Zhuodaoquan Interchange)

图2中轨迹部分为选取的验证路段，标记点为主要的转弯路段，图3为对应的横向速度(vx)与车辆行驶速度(vy)、历元间航向角差(da)关系。根据NHC假设，车辆横向的速度vx应为0，而由图3可知，vx不为0，即存在横向速度偏差，车辆实际运动时并不能完全满足NHC假设：图3(a)为vx与vy的关系图，可以发现两者在数值上有明显的正相关性，在车速vy增大/减小时，vx数值也相应地增大/减小(图3(a)中标记部分尤其明显)，即NHC横向速度噪声受车辆前进速度影响；图3(b)为vx与da的关系图，标记处为图2对应标记的主要转弯路段，可以发现在转弯路段，vx数值的增大/减少主要由da的增大/减小引起，其中b处进行大幅度转弯运动时，vx变化尤其明显，即NHC横向速度噪声受车辆转弯影响。综上可知，NHC横向速度噪声项σNHC,x受车辆速度与车辆转弯的共同影响。

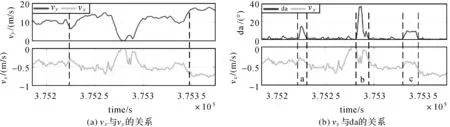
图3 横向速度与车辆行驶速度、历元间航向角差Fig.3 Lateral speed, vehicle speed, heading angle difference between epochs

本文根据文献[18]，提出了基于车辆运动状态的NHC噪声自适应模型。如前所述，σNHC,x受车辆速度与车辆转弯的共同影响，车辆的速度可直接从车辆CAN总线获取(vod)，而车辆转弯的判断条件可表示为[18]

(16)

式中，|δY|为航向角变化值；λi(i=1,2,3)为角度变化率阈值；vi(i=1,2,3)为速度阈值；详细可参考文献[18]。

根据式(16)可判断车辆是否转弯，当车辆存在转弯运动时，根据车辆行驶速度和转弯角度的大小，动态调整NHC噪声项σNHC,x

σNHC,x=vod·|δY|·SY

(17)

式中，SY为设定的自适应比例因子。

为减少过松或者过紧的噪声约束导致滤波结果异常，在进行滤波更新时，首先根据式(17)计算噪声项σNHC,x，再进行自适应调整

(18)

3 实测分析

本文采用两组实测车载数据进行验证与分析，采用的MEMS IMU为Bosch Sensortec公司生产的IMU BMI160，其部分参数见表1。里程计数据直接从车辆CAN总线中获取，参考值为加拿大NovAtel公司的SPAN-CPT组合导航结果。

表1 BMI160参数Tab.1 Parameters of BMI160

3.1 测试结果1

车载数据1于2020年9月10日在武汉市洪山区采集获得，IMU数据采样率为100 Hz，GNSS数据采样率为1 Hz，从车辆CAN总线中获得的里程计数据采样率为20 Hz。为验证本文算法，选取了车辆行驶110 s总长约1.3 km的转弯路段模拟GNSS中断。轨迹图和GNSS中断区间如图4所示，图中箭头指示车辆的行驶方向。可以发现，车辆在GNSS中断后共经过了两段360°转弯路段，能够充分验证车辆转向时对NHC约束性能的影响。

图4 实测轨迹1与模拟GNSS中断区间(白线轨迹)Fig.4 Measured trajectory 1 and simulated GNSS interruption interval (White line trajectory)

在GNSS中断期间，根据式(10)，使用里程计速度与NHC结合进行测量更新。本文设计了不同数据处理方案进行对比见表2，其中方案3、方案4用于说明NHC对于OD/SINS组合系统的有效性，方案1、方案2用于验证本文所构建算法的有效性。由于σNHC,x主要影响水平位置精度，因此，本文主要从水平轨迹、水平误差序列及其统计值对比分析不同方案的定位性能。

表2 数据处理方案Tab.2 Data processing strategy

图5为使用不同方案得到的GNSS中断期间的水平轨迹对比，可以发现在GNSS信号中断后，车辆随即进入转弯路段。可以发现采用NHC辅助OD/SINS导航的方案1、方案2的轨迹与实际运动轨迹基本吻合；采用纯SINS解算的方案3在GNSS信号中断后误差迅速发散，轨迹已经完全偏离实际轨迹；仅采用OD辅助SINS导航的方案4在GNSS信号中断后在第一个转弯路段整体维持在车道线附近，在车辆驶出第一个转弯路段进入直线后，轨迹出现了明显发散的现象。由此可知，GNSS中断后误差的发散是由于SINS带入的。相比于单OD/SINS组合导航，使用NHC引入了右向与垂向的速度观测值，从而提高了卡尔曼滤波估计器的冗余度，有利于提升系统的抗差性和稳定性。由此可见，使用NHC辅助可以显著提升OD/SINS组合系统的可用性(由表3的统计结果可以进一步佐证)。因此，下文主要针对本文所提出的自适应噪声方案与传统固定噪声的方案进行对比分析。

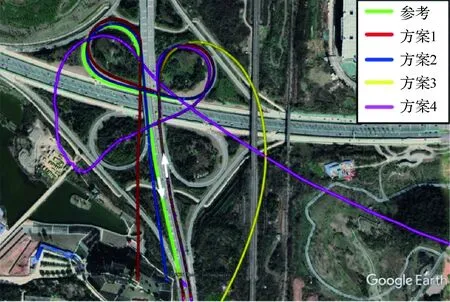
图5 不同方案的水平轨迹——数据1Fig.5 Horizontal trajectory of different strategies—data 1

图6为GNSS中断期间分别使用方案1、方案2得到的水平轨迹对比。可以发现，在第1个转弯路段中，两种方案解算的轨迹都与参考轨迹基本重合，整体无明显发散的现象。在车辆驶出第一个转弯路段进入直线时，使用方案1，车辆未能准确进入直线路段，轨迹开始出现发散现象，明显偏离车道；而方案2轨迹虽然也有一定的发散，但整体还是可以维持在车道附近，没有明显发散。在第2个弯道部分，方案1轨迹出现了明显偏移的现象，而方案2轨迹与参考轨迹符合程度较好。在车辆驶出弯道进入直线路段后，方案1、方案2都可以维持直线行驶，但方案1由于之前的误差累积，轨迹迅速发散，而方案2轨迹发散程度明显更小，能与实际轨迹维持较高的符合度。

图6 不同方案的水平轨迹(方案1与方案2)——数据1Fig.6 Horizontal trajectory of different strategies(strategy 1 & strategy 2)—data 1

图7为水平误差序列图，可以发现在前35 s部分(第1个转弯路段)， 由于使用与直线行驶时一样的固定NHC噪声项， 组合导航滤波结果的误差累积加快，方案1的误差曲线已经出现波动，而方案2由于可以正确探测到车辆的转弯，对NHC噪声项进行了自适应调整，误差曲线基本维持在0附近。在第60 s左右时(第2个转弯路段中段)，方案1的水平误差已经达到了30 m，而方案2误差在10 m左右。第80 s(车辆驶出弯道进入直线)后，由于误差累积，方案1的右向误差相比于方案2迅速发散，进而导致水平误差的迅速发散。

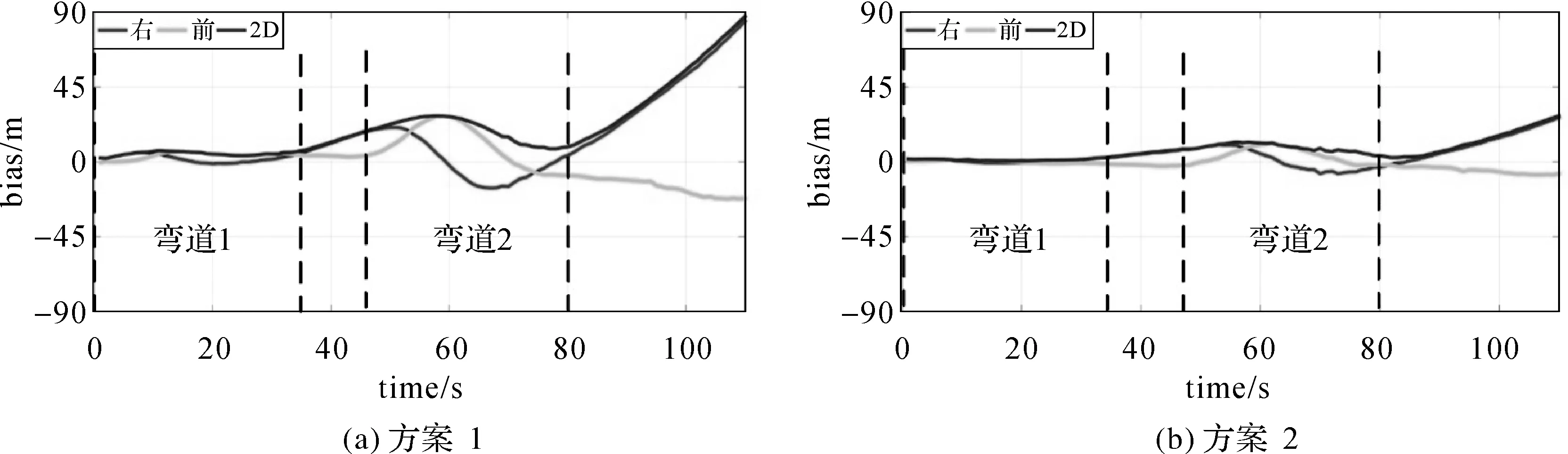
图7 误差序列图——数据1Fig.7 Error sequence diagram—data 1

图8为两种方案给出的NHC噪声对比序列，方案1使用固定的σNHC,x值(设置为0.01)，方案2根据式(18)自适应调整σNHC,x值，可以发现方案1在转弯与直线路段都使用了固定的σNHC,x值，在转弯路段不能完全符合车辆实际运动状态，因此最终定位误差较大。而由方案2给出的σNHC,x在实时调整，σNHC,x在转弯路段明显增大，更加符合车辆实际运动状态，因此最终定位误差相对较小。由此可见，本文构建的基于车辆运动状态的NHC噪声自适应模型，相比于固定噪声的NHC模型，通过自适应调整噪声，限制了NHC方法在转弯状态下的对观测结果的影响权重。

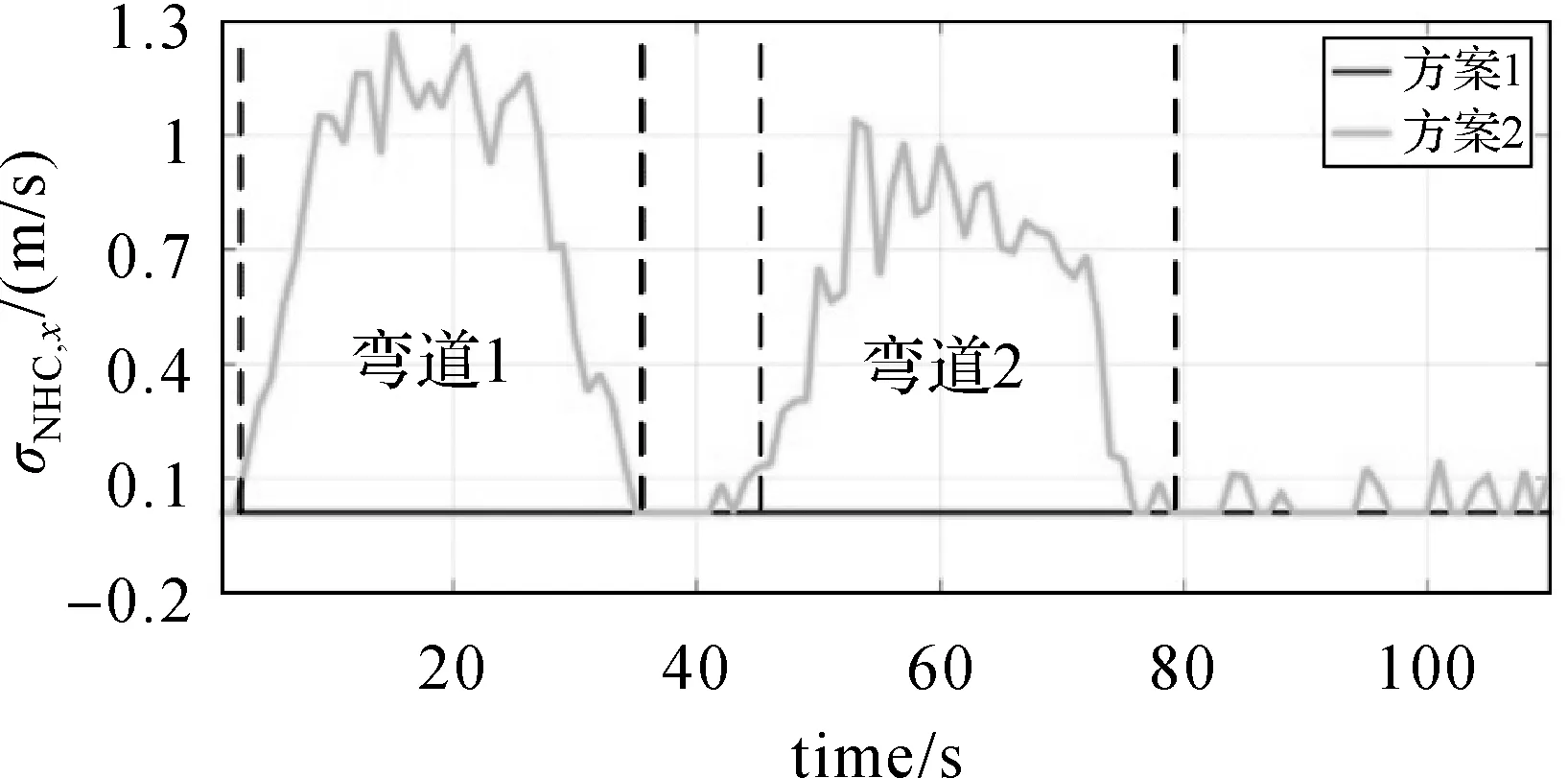
图8 不同方案NHC噪声对比序列图——数据1Fig.8 NHC noise comparison sequence diagram of different strategies—data 1

表3给出了不同数据处理方案得到的最大位置误差结果。在GNSS信号中断的110 s期间，采用纯SINS解算的方案3误差最大，使用OD/SINS组合的方案4相比于方案3的误差明显减小，但明显大于使用了NHC的方案1、方案2，进一步说明了使用NHC辅助可以显著提升OD/SINS组合系统的可用性。与方案1使用固定的NHC噪声项相比，方案2使用自适应的NHC噪声项的最大右向误差从84.60 m减小到26.66 m，最大前向误差从27.52 m减小到11.08 m，最大水平误差从87.40 m减小到了27.61 m，结果表明本文构建的NHC噪声自适应算法是有效的。

表3 不同方案统计指标对比——数据1Tab.3 Comparison of statistical indicators of different schemes—data 1 m

3.2 测试结果2

为进一步验证本文所构建自适应噪声方案相比于固定噪声方案的有效性，选取一段实测直线路段车载数据进行分析。车载数据2于2020年9月10日在武汉市洪山区采集获得，所采用的设备与数据记录、处理方案均与车载数据1一致。

图9为轨迹图和GNSS中断区间示意图，图中箭头指示车辆的行驶方向。可见GNSS中断路段为直线路段，GNSS中断时长为74 s，路线长度约为700 m，车辆进行变速运动。

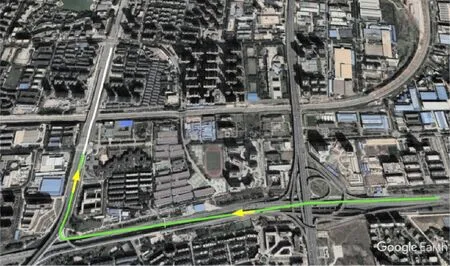
图9 实测轨迹2与模拟GNSS中断区间Fig.9 Measured trajectory 2 and simulated GNSS interruption interval

图10为两种方案给出的NHC噪声对比序列，方案1使用固定的σNHC,x值(设置为0.01)，方案2根据式(18)自适应调整σNHC,x值，可见在变速运动下，方案2会自适应调整σNHC,x值，因此两种方案的结果也会存在差别。

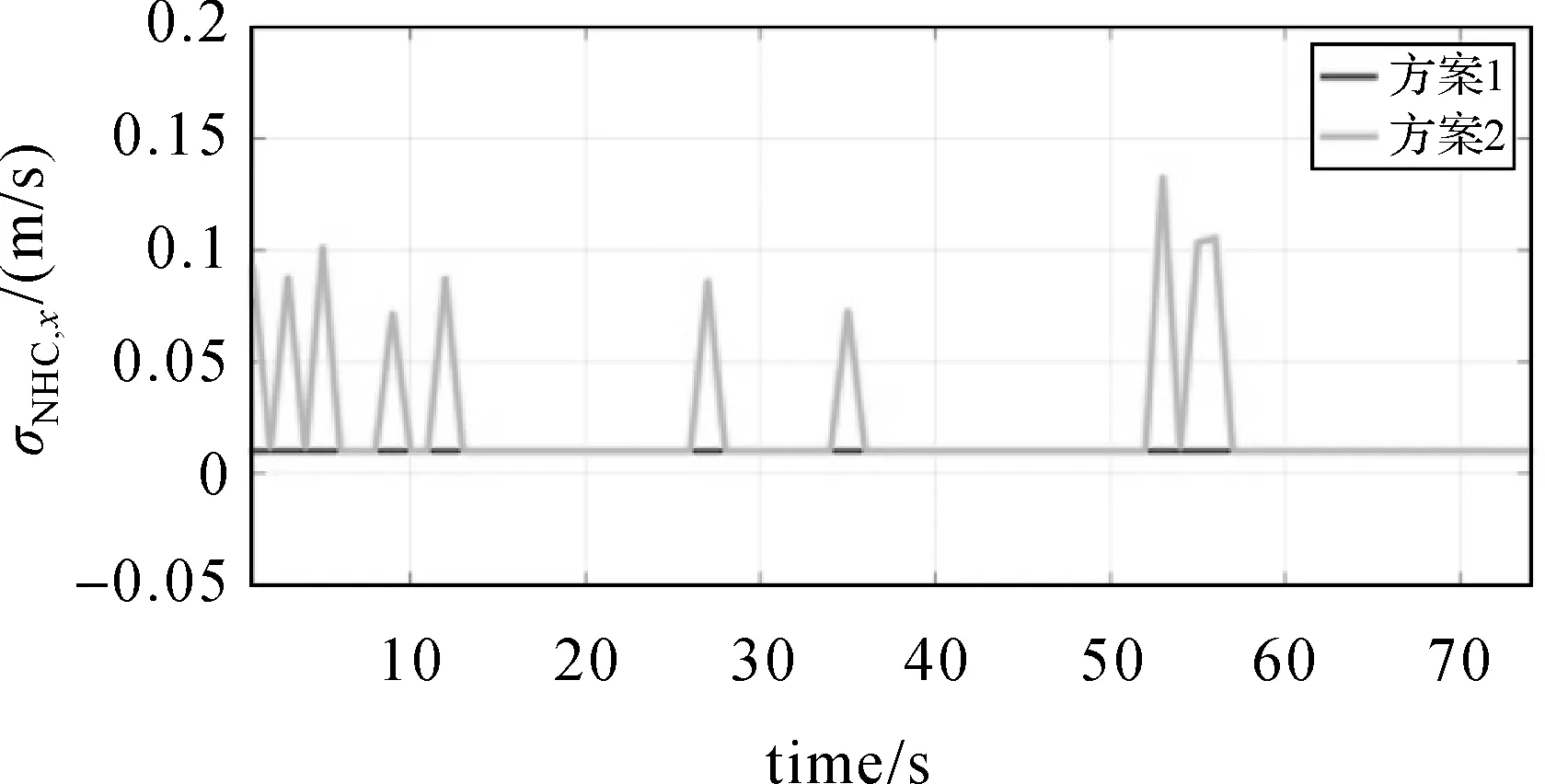
图10 不同方案NHC噪声对比序列图——数据2Fig.10 NHC noise comparison sequence diagram of different strategies—data 2

图11为水平轨迹对比图，表4为不同数据处理方案得到的最大位置误差结果。由结果可见，在GNSS中断74 s的直线路段中，采用本文所构建的自适应噪声方案2，最大水平误差不超过10 m，而采用固定噪声的方案1时，最大水平误差超过了60 m，结果表明本文构建的NHC噪声自适应算法是有效的。

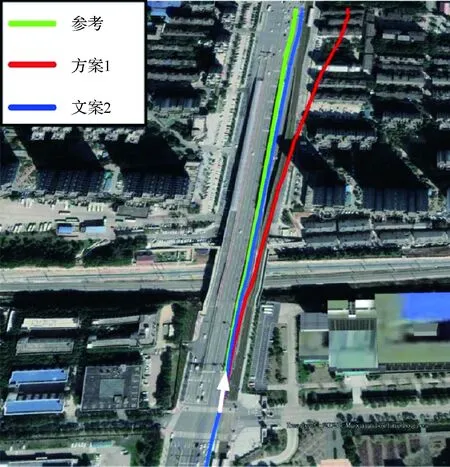
图11 不同方案的水平轨迹(方案1与方案2)——数据2Fig.11 Horizontal trajectory of different strategies(strategy 1& strategy 2)—data 2

表4 不同方案统计指标对比——数据2Tab.4 Comparison of statistical indicators of different schemes—data 2 m

综合以上分析可知，根据车辆的运动状态，使用NHC噪声自适应的方法能更加有效地利用NHC信息，可有效地提高车辆组合导航定位的精度。所选场景的实测结果表明，相比于固定噪声的NHC/OD/SINS组合算法，采用自适应噪声的NHC/OD/SINS组合算法，在110 s的GNSS信号中断、车辆连续转弯的情况下，最大水平位置误差减小了68.4%；在74 s的GNSS信号中断、车辆直线行驶的情况下，最大水平位置误差减小了87.3%。

4 结 语

在地面车载组合导航中，当GNSS信号中断时采用NHC/OD/SINS组合可以抑制组合导航结果的误差发散。本文构建的基于车辆运动状态的NHC噪声自适应方法，通过IMU测量值与车辆CAN总线提供的速度测量值判断车辆的运动状态。所选场景的实测结果表明，该自适应方法能够较好地抑制GNSS中断期间组合导航系统的误差发散，采用自适应噪声的NHC/OD/SINS组合算法的最大水平位置相比于固定噪声的NHC/OD/SINS组合算法，在110 s的GNSS中断的连续转弯路段，最大水平位置误差减小了68.4%；在74 s的GNSS中断的直线路段，最大水平位置误差减小了87.4%。