华龙一号失水事故后安全壳内气溶胶自然沉降现象研究
2022-03-07刘建昌陈忆晨陈韵茵沈永刚张亚培苏光辉
刘建昌,陈忆晨,余 剑,陈韵茵,沈永刚,*,张亚培,苏光辉
(1. 中广核研究院有限公司,深圳 518000; 2. 西安交通大学,西安 710000)
对于未采用喷淋系统的安全壳设计,安全壳内的自然沉降过程是放射性核素在安全壳内的一个重要去除机理。
在参考文献[1]中,对安全壳内放射性核素的自然沉降研究进行了充分的调研,并给出了国内外开展的自然沉降实验和开发的沉降模型。安全壳内放射性核素的主要沉降机理包括重力沉降、扩散电泳、热电泳和布朗扩散,此外还有湍流扩散和湍流凝聚等。总的趋势为:安全壳内大气中粒径较大的放射性核素沉降下来,粒径较小的放射性核素继续悬浮在大气中。放射性核素在安全壳内的沉降过程与核素几何形状、粒径分布、核素密度和安全壳内的热工水力状态有关。
华龙一号在分析事故后向环境的放射性释放时,未考虑安全壳内的自然沉降过程。对于释放到安全壳内的放射性核素,仅考虑在瞬态过程中的自然衰变。从放射性释放角度而言,这一分析假设是非常保守的。PHÉBUS-FP实验研究发现,在严重事故工况下,堆芯熔化阶段和随后的20min内,安全壳内大气中80%的核素会沉积到安全壳壁面[2,3]。本文将对华龙一号发生冷管段双端剪切断裂事故后,安全壳内气溶胶的自然沉降现象开展研究。
1 气溶胶的自然沉降模型
气溶胶在安全壳内的自然沉降机理,包括重力沉降、扩散电泳、热电泳、布朗扩散、湍流扩散和湍流凝聚等。目前的研究表明,前四种机理在安全壳内气溶胶的自然沉降过程中起主导作用,湍流扩散、湍流凝聚等机理对释放到安全壳内气溶胶的去除贡献很小,因此本文忽略这些去除机理的作用,仅考虑前四种自然沉降过程。
1.1 重力沉降
在重力的作用下,悬浮在安全壳内大气中的气溶胶会向下运动,最终沉降在朝上的表面上。
对于气溶胶,重力沉降速率υs可通过求解最终下落速度得到[4]:

式中:
ρp为气溶胶密度;
r为气溶胶的半径,dp=2r;
μ为气体的粘度;
Cn为滑移修正因子,是Kn数的函数:
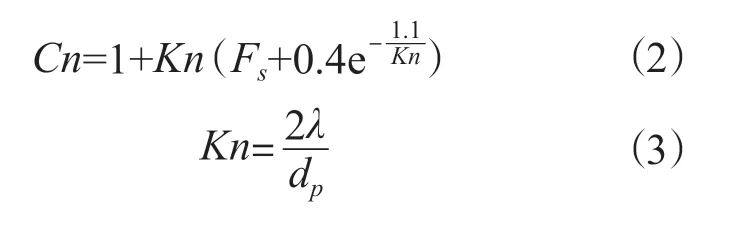
φ为动力形状因子,与气溶胶的形状有关:

公式(2)至公式(5)中:
Fs为滑移因子;
λ为气体分子平均自由程;
ρv为空泡物质的密度;
ε为空泡物质的份额。
从公式(1)可以看出,重力沉降速率υs与的平方成正比;气溶胶半径越大,重力沉降速率越快。
1.2 扩散电泳
扩散电泳是指粒子被由冷凝蒸汽形成的流动扫向壁面的过程。气溶胶的扩散电泳沉降速率υd可用下式进行计算[5]:
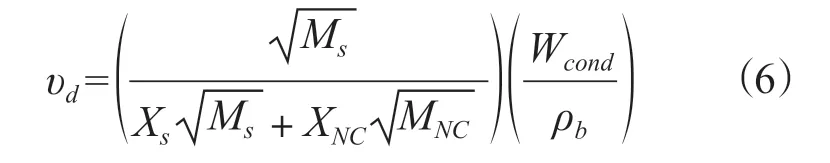
式中:
Ms、MNC分别为水和不可凝气体的摩尔质量;
Xs、XNC分别为气体中水蒸气和不可凝气体所占的摩尔份额;
Wcond为表面凝结水质量流量;
ρs、ρd分别为水蒸气和不可凝气体的密度。
从公式(6)可以看出,气溶胶在冷凝表面的沉降速率与粒子尺寸无关,与蒸汽在表面上的冷凝速率成正比。
1.3 热电泳
热电泳是粒子在安全壳内大气与表面(如安全壳内壁等)之间的温度梯度的影响下,向表面迁移的过程。热电泳的沉降速率υth可用下式进行计算[6]:

式中:
α=kg/kp;kg和kp分别为气体和气溶胶 的热导率;
μg和ρg分别为气体的粘度和密度;
Cs为滑移修正系数;
CT为热量修正系数;
CM为动量修正系数。
对于壁面附近的温度梯度,根据壁面处热流密度φs计算得到:

参考文献[5]中给出的热量修正系数推荐值为2.25。参考文献[6]中根据前人研究成果进一步指出,从分子运动论得到的动量修正系数、热量修正系数和滑移修正系数的最佳修正值分别为CM=1.14、CT=2.18和Cs=1.17。
1.4 布朗扩散
布朗扩散又称分子扩散,指的是粒子在流体内所做的无序不规则运动。这种无序运动是在一定的无序热运动下,气体分子和粒子间的碰撞造成的。不同方向的碰撞动量所形成的冲力大小无法平衡,就形成了这种布朗运动。静止条件下气体中粒子的扩散沉降层流流动中的粒子扩散均属于布朗扩散。布朗扩散沉降速率υdiff可用下式计算得到[5]:
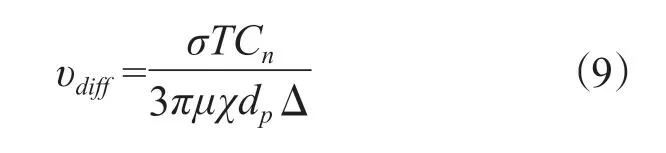
式中:
σ为波尔兹曼常数;
T为安全壳内大气温度;
μ为气体的粘度;
χ为气溶胶动力学形状因子;
Δ为扩散边界层厚度。
1.5 自然沉降去除因子
根据2.1节至2.4节中给出的自然沉降速率计算公式,可以计算得到气溶胶的自然沉降去除因子λ:
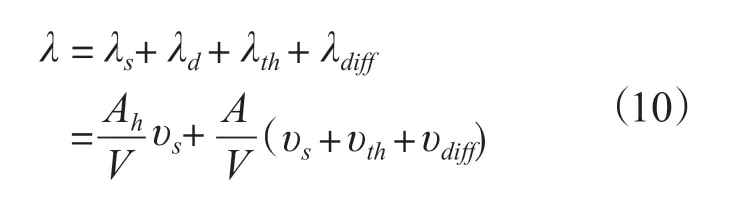
式中:
Ah为朝上的地板或设备表面面积;
A为安全壳内可供沉降的所有表面面积(包括Ah);
V为安全壳内自由容积。
1.6 安全壳内大气中气溶胶质量变化
从1.1节至1.4节中给出的自然沉降速率计算公式可以看出,气溶胶的自然沉降速率与气溶胶的粒径有关。在分析安全壳内大气中气溶胶质量变化时,应对不同粒径的自然沉降过程进行分析,计算不同粒径气溶胶的质量变化,进而得到安全壳内大气中气溶胶总质量Ql(t):
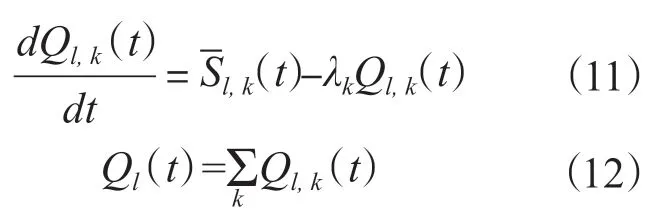
式(12)中,仅考虑了安全壳内的自然沉降去除过程,没有考虑气溶胶凝聚导致的气溶胶粒径变化。其中,Sl, k为气溶胶的注入速率;λk为某一粒径气溶胶的自然沉降因子,根据公式(10)进行求解。
1.7 气溶胶粒径分布特性
从前文中给出的气溶胶沉降模型可以看出,安全壳内气溶胶自然沉降过程与气溶胶的粒径分布特性有关。参考文献[1]中指出,气溶胶的粒径为0.01 μm到20 μm,在事故工况下气溶胶的浓度小于100 g/m3。在实际分析中很难以微观的角度去分析单个气溶胶粒子的行为,通常采用统计方法去分析气溶胶特性。在分析过程中认为气溶胶粒径分布是连续变化的。假设气溶胶粒径呈现对数正态分布,即[7]
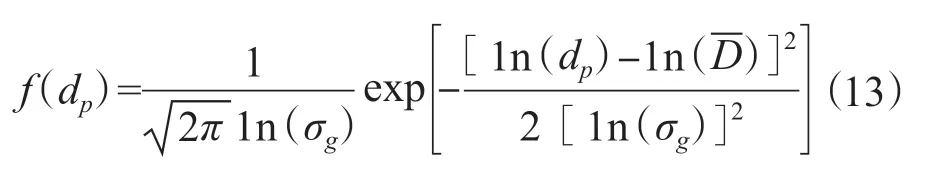
式中,D和σg分别为几何平均直径和几何标准偏差。
2 华龙一号安全壳内气溶胶自然沉降现象
从第1节中给出的沉降 模型可以看出,气溶胶在安全壳内的沉降过程与事故后安全壳内热工响应有关,包括壁面的冷凝质量流量、壁面温度梯度、温度分布等。破口位置、破口尺寸不同,安全壳热工响应不同,气溶胶在安全壳内的自然沉降速率也不同。在考虑事故安全壳内气溶胶的自然沉降过程时,需要结合破口位置、破口尺寸,开展安全壳热工响应分析;根据不同事故的安全壳内冷凝质量流量、壁面温度梯度、温度分布等,以及释放到安全壳内气溶胶质量,评估气溶胶在安全壳内的自然沉降过程。
本文中假设华龙一号发生冷管段双端剪切大破口失水事故,分析该事故条件下的安全壳内气溶胶(本文分析中以CsI气溶胶为分析对象)自然沉降现象。
通过采用CATHARE GB程序和CONPATE程序分析冷管段双端剪切大破口失水事故后安全壳内热工响应,可以得到事故后安全壳内压力和温度响应,以及壁面的温度梯度和冷凝水流量。本文分析的是事故后安全壳内气溶胶的沉降过程,不再对事故后安全壳内热工响应进行详细展开。分析得到的事故后安全壳内压力、冷凝水流量和壁面温度梯度分别如图1至图3所示。

图1 LOCA后安全壳内压力Fig. 1 Containment Pressure of LOCA
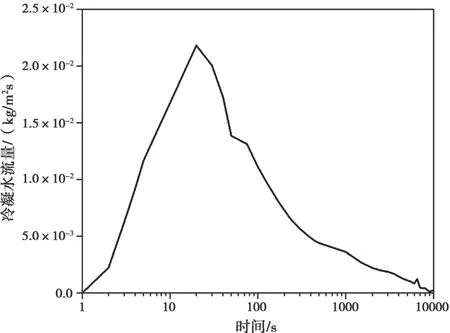
图2 LOCA后冷凝水流量Fig. 2 Mass Flow Rate of Condensation Water of LOCA

图3 LOCA后壁面温度梯度Fig. 3 Wall Temperature Gradient of LOCA
在分析假设事故后30 s,事故导致全堆芯燃料包壳发生破损,包壳间隙中碘和碱金属全部释放到安全壳内[8],根据堆芯积存量和包壳间隙中碘和铯的份额可以计算得到释放到安全壳内的气溶胶质量。包壳间隙中碘和铯的份额假设为5%[8],计算可以得到释放到安全壳内CsI的总质量为89 g。
安全壳内自由容积取72000 m3。对于安全壳内可供沉降表面积,即天花板、墙体和水平地板分别为2200 m2、6700 m2和1650 m2。
除事故后安全壳内热工响应外,沉降过程还与气溶胶的粒径有关。对于不同粒径的气溶胶,重力沉降和布朗扩散的沉降速率如图4所示[1]。可以看出,随着气溶胶粒径的增大,布朗扩散的沉降速率越小,而重力沉降速率越大。在研究事故后安全壳内气溶胶的沉降现象时,需要针对不同的气溶胶粒径开展分析。

图4 不同粒径下重力沉降和布朗扩散的沉降速率[1]Fig. 4 Comparison of deposition velocities of gravitational and diff usion deposition for diff erent partical diameters
在分析安全壳内气溶胶沉降现象时,动量修正系数、热量修正系数和滑移修正系数分别取CM=1.14、CT=2.18和Cs=1.17[6]。从重力沉降模型可以看出,动力形状因子φ越大,重力沉降速率越小,为保守评估气溶胶在安全壳内的沉降过程,假设气溶胶内的空泡中充满空气,空泡份额假设为0.9,可根据公式(4)计算形状因子φ。
2.1 气溶胶粒径分布特性对沉降现象的影响研究
本小节中将首先分析不同气溶胶粒径对安全壳内沉降现象的影响。假设释放到安全壳内的气溶胶粒径满足对数正态分布,在研究气溶胶粒径对沉降现象的影响时,可以通过分析不同几何平均直径对气溶胶沉降速率的影响。
本节中选取0.4 μm、1 μm、3 μm和10 μm四种不同几何平均直径,评估气溶胶几何平均直径对沉降现象的影响。在分析安全壳内大气中气溶胶质量变化时,按气溶胶粒径将释放到安全壳内的气溶胶划分为10组,每一组内的气溶胶质量 可以根据公式(13)计算得到。在计算时,假设几何标准偏差σg=1.8。
在分析气溶胶粒径对沉降现象的影响时,假设包壳间隙中释放的CsI瞬时释放到安全壳内。对于上述四种不同几何平均直径,安全壳内大气中悬浮气溶胶份额(悬浮气溶胶质量与释放到安全壳内气溶胶总量之比)如图5所示,在计算时间终止时刻(10000 s),沉降的气溶胶质量份额如表1所示。
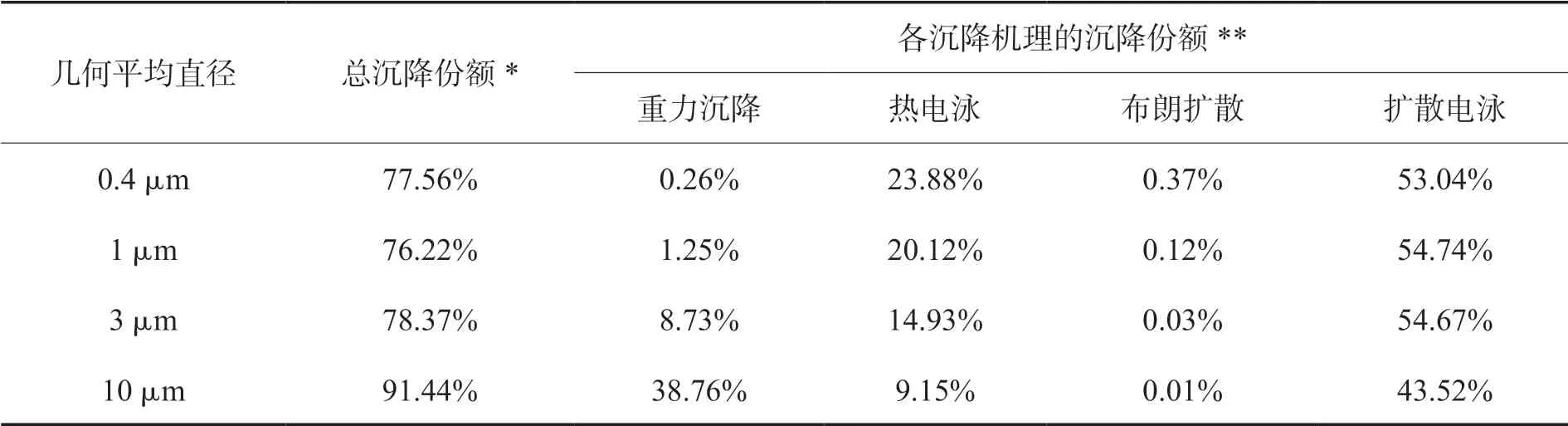
表1 自然沉降机理的贡献Table 1 Contributions of Diff erent Natural Deposition Mechanisms

图5 气溶胶粒径对沉降现象的影响Fig. 5 Eff ects of Aerosol Diameter on Natural Deposition
从分析结果可以看出,随着气溶胶几何平均直径的增大,沉降的气溶胶质量呈先减小后增大的趋势。这主要受重力沉降、热电泳两种沉降机理的影响。随着气溶胶几何平均直径的增大,释放到安全壳内的气溶胶中,大直径气溶胶的份额越高,重力沉降机理的贡献越大,而热电泳沉降机理的贡献逐渐减小。扩散电泳与气溶胶的尺寸无关。当气溶胶直径较小时,扩散电泳是主要的沉降机理,此时气溶胶几何平均直径的变化对总沉降份额的影响较小;随着几何平均直径的进一步增大,重力沉降的贡献逐渐增大,而热电泳的贡献逐渐减小,部分直径较大的气溶胶在重力沉降的作用下沉降到水平朝上的表面上,扩散电泳的贡献逐渐减小。对于所考虑的工况,布朗扩散沉降机理的贡献均很小。
2.2 气溶胶释放速率对沉降现象的影响研究
在3.1节中,假设在事故后30s,燃料包壳间隙中释放的碘和铯瞬时释放到安全壳内。参考文献[8]、参考文献[9]和参考文献[10]中,指出包壳间隙释放的持续释放时间为0.5 h,在包壳间隙释放阶段,对于放射性核素的释放过程考虑线性释放。
在本节中,假设在30 s后,包壳间隙中释放的碘和铯以均匀速率释放到安全壳内,释放持续时间为0.5 h。在分析中,假设释放到安全壳内的气溶胶粒径满足对数正态分布,几何平均直径=0.4 μm、几何标准偏差σg=1.8。
线性释放假设下,安全壳内大气中悬浮气溶胶质量和沉降质量如图6所示。对比线性释放和瞬时释放两种气溶胶释放假设可以看出,在分析安全壳内气溶胶沉降过程时,相比线性释放假设,采用瞬时释放假设,高估了瞬态过程中的沉降质量。这主要与气溶胶在安全壳内的自然沉降时间有关。释放到安全壳内后,在自然沉降机理的作用下,气溶胶开始逐渐沉降到安全壳内不同表面上。当采用瞬时释放假设时,高估了气溶胶的自然沉降时间,进而高估了气溶胶在安全壳内的沉降质量。因此,在分析事故后向环境的放射性释放量时,若考虑气溶胶在安全壳内的自然沉降过程,不应采用瞬时释放假设,而应该考虑气溶胶从堆芯向安全壳内的释放过程。
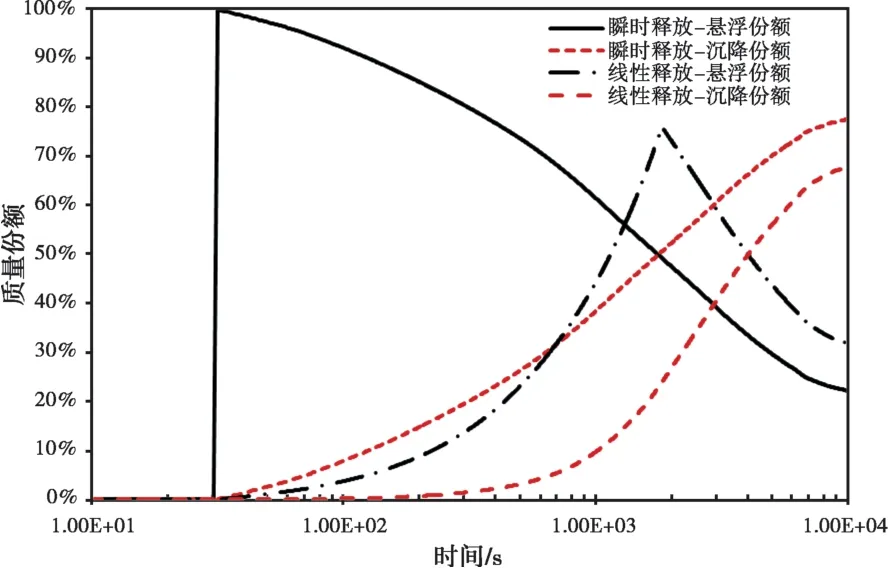
图6 气溶胶释放假设对沉降现象的影响Fig. 6 Eff ect of Aerosol Release Assumption on Natural Deposition
3 总结
本文给出了重力沉降、扩散电泳、热电泳和布朗扩散四种自然沉降机理的沉降速率分析模型。
针对华龙一号冷管段双端剪切大破口失水事故,开展了安全壳内气溶胶自然沉降现象研究,分析了气溶胶粒径分布特性、气溶胶释放假设对自然沉降现象的影响。分析结果表明:
(1)对于冷管段双端剪切大破口失水事故,布朗扩散机理的贡献很小,对于粒径不是很大的气溶胶,扩散电泳和热电泳是主导的自然沉降机理;
(2)气溶胶的粒径分布特性影响自然沉降过程,即粒径越大,重力沉降机理的贡献越大,而热电泳沉降机理的贡献机理逐渐减小;
(3)相比线性释放假设,采用瞬时释放假设,高估了瞬态过程中的沉降质量。
从分析结果可以看出,对于冷管段双端剪切大破口失水事故,对于粒径不是很大的气溶胶,扩散电泳和热电泳是主导的自然沉降机理。从沉降模型可以看出,扩散电泳和热电泳两种机理的沉降速率,分别与冷凝速率、壁面温度梯度成正比。对于不同尺寸、不同破口位置的失水事故,瞬态过程中冷凝速率、壁面温度梯度均不相同,在考虑不同事故的安全壳内自然沉降过程时,应对不同事故开展安全壳热工响应分析,根据安全壳热工响应分析结果,分别分析不同事故下气溶胶在安全壳内的自然沉降速率。
需要进一步指出的是,对于不同粒径分布的气溶胶,几种自然沉降机理的贡献不同,本文在分析安全壳内气溶胶沉降过程时并未考虑气溶胶的凝聚生长。当气溶胶主要为较大粒径的颗粒时,不考虑气溶胶的凝聚生长,从评估安全壳内大气中气溶胶质量角度而言是保守的;但当释放到安全壳内的大部分气溶胶为小粒径的颗粒时,不考虑气溶胶的凝聚生长,有可能会高估沉降的气溶胶质量。对于事故后安全壳内的沉降过程,应结合释放到安全壳内气溶胶的粒径分布特性,合理地评估气溶胶的凝聚生长过程,进而保守评估气溶胶在安全壳内的自然沉降速率。
