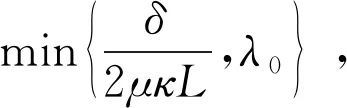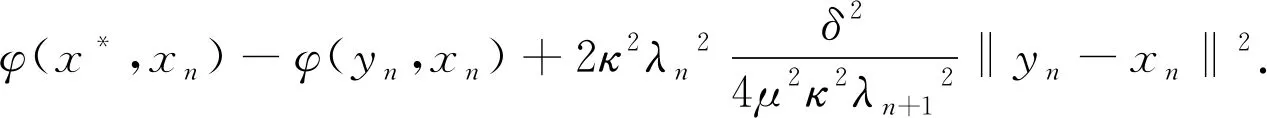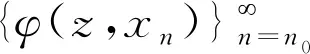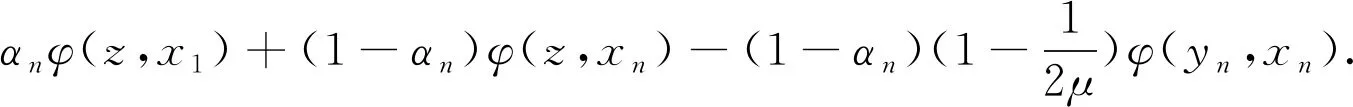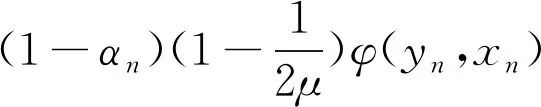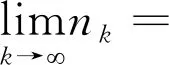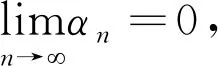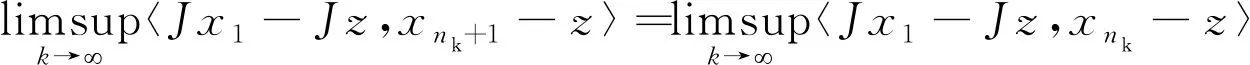求解Banach空间中变分不等式新的单投影算法
2022-03-07周韵红
周韵红
(西华师范大学数学与信息学院,四川南充 637009)
0 引言
设E是一个实Banach空间,E*是其对偶空间,‖·‖和‖·‖E*分别是E和E*的范数,〈f,x〉是f∈E*在点x∈E处的函数值.设C是E中的一个非空闭凸子集,并且A:E→E*是一个Lipschitz连续映射.在本文中,考虑下面的变分不等式问题(VIP),即找x∈C,使得下面式子成立
〈Ax,y-x〉≥0,∀y∈C.
(1)
用VI(A,C)来表示变分不等式问题(1),且用S表示它的解集.
变分不等式问题是数学最优化理论中一个有用而有效的工具.它统一了应用数学中的几个重要概念:必要条件、网络平衡问题、互补问题和算子方程的方程组.对于VIP,最简单的投影方法是只在可行集上执行一次投影的梯度方法,然而这种方法的收敛性需要一个轻微的强假设,即要求算子是强单调的或反强单调的.Korpelevich[1]提出了一个解决鞍点问题的外梯(EGM)算法,它使我们避免了上述的强假设.在那之后,它被发展并推广到有限维和无限维的Hilbert空间中的VIP.在映射A是单调的和L-Lipschitz连续的假设下,保证了该方法的收敛性.该算法(EGM)的迭代格式如下:
(2)
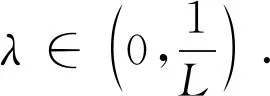
(3)
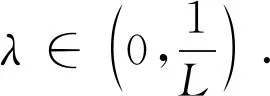
(4)
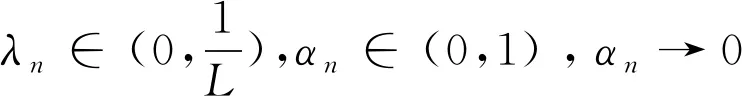
1 预备知识
本节给出一些概念和预备知识.
设E是一个实的Banach空间,C是E中的一个非空闭凸子集.{xn}弱收敛到x表示为
xn→x(n→∞)(弱),{xn}强收敛到x表示为xn→x(n→∞).
正规对偶映射J:E→E*定义为Jx={x*∈E*|〈x*,x〉=‖x*‖2=‖x‖2}.如果对所有的x,y∈SE,下式极限存在
(5)
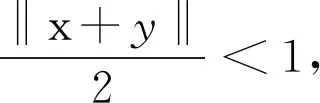
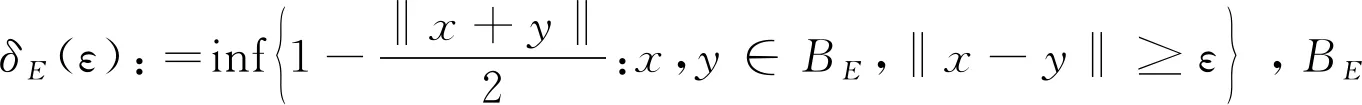
如果存在c>0使得对于所有的ε∈[0,2]都有δE(ε)≥cε2,则称空间E是2-一致凸的.显然,所有的Hilbert空间都是2-一致光滑和2-一致光滑凸的.此外,所有的LP(1 引理1.1空间E是2-一致凸的当且仅当存在μE≥1,使得 (6) 对于所有的x,y∈E,所有满足(6)式的μE≥1所构成的集合中的最小值记为μ,称为空间E的2-一致凸性系数.显然μ=1当且仅当E是Hilbert空间. (i)E是2-一致凸的. 定义1.1假设C⊆E是一个非空集合,A:C→E*是一个连续映射,则有 (i)A是单调的当且仅当 〈Ax-Ay,x-y〉≥0,∀x,y∈C; (ii)A是L-Lipschitz连续的(L>0),即存在常数L>0,使得 ‖Ax-Ay‖≤L‖x-y‖,∀x,y∈C. 下面介绍一个非常有用的函数,即Lyapunovfunctionalφ:E×E→R,其定义如下: φ(x,y):=‖x‖2-2〈x,Jy〉+‖y‖2,∀x,y∈E 显然,φ(x,y)≥(‖x‖-‖y‖)2≥0. SCADA系统是进行电网数据采集与监控的系统。通过SCADA系统检验开关状态,去除不良数据,计算出比SCADA遥测数据更准确的运行方式,以及未装量测的设备潮流和难以测量的电气量。数据在SCADA中需有定义,没有定义的数据不从SCADA获取。 引理1.4令E是一个实的、一致凸的、光滑的Banach空间,则下面的式子成立: (i)φ(x,y)=φ(x,z)+φ(z,y)+2〈x-z,Jz-Jy〉,∀x,y,z∈E; (ii)φ(x,y)+φ(y,x)=2〈x-y,Jx-Jy〉,∀x,y∈E. 接下来介绍一个相关的函数,它对文章后面的收敛分析非常有用.假设C⊆E是实的、一致凸的Banach空间E的一个非空集合.则函数V:E×E*→R,其定义为: 如果算子ΠC:E→C⊂E将函数φ(y,z)的最小值点与任意固定点z∈E相联系,即下面最小值问题的解,则称该算子称为广义投影算子,其定义如下 下面将介绍ΠC的一些性质. 引理1.5下述结论成立. (ii)广义投影算子产生了相关函数φ(w,z)的一个最优值,即 (iii)V(x*,x)+2〈J-1x*-x,y*〉≤V(x*+y*,x),∀x∈E,x*,y*∈E*. 引理1.6假设E是一个2-一致凸的Banach空间,则存在μ≥1使得 引理1.7令{an}是一个实数列,使得这里存在n的一个子序列{ni}满足ani amk≤amk+1且ak≤amk+1.实际上,mk={j≤k:aj 引理1.8令{an}是一个非负实数列并且满足下面的关系: 则有an→0(n→∞). 引理1.9C是E一个非空闭凸子集.令A:C→E*是一个连续单调算子并且z∈C,则有 z∈S⟺〈Ax,x-z〉≥0对所有的x∈C都成立. 这一节介绍了求解Banach空间中单调变分不等式问题的一种新的迭代算法.为了给出该算法并证明其收敛性,现作如下假设: 假设1 (a)可行集C上是实的2-一致凸、光滑的Banach空间E的一个非空闭凸子集. A:E→E*在C上是单调的且在E上是L-Lipshitz连续的. (c)VI(A,C)的解集S是非空的. 现在,讨论以下算法用来解决单调变分不等式的收敛性.该算法(算法A)如下: (步骤0)令λ0>0,x0∈E是初始值,δ∈(0,1). (步骤1)已知xn,计算yn=ΠCJ-1(Jxn-λnAxn),如果xn=yn,则停止;否则转向步骤2. (步骤2)计算wn=J-1[Jyn-λn(Ayn-Axn)]和xn+1=J-1[αnJx1+(1-αn)Jwn]. (步骤3)计算 这里μ是E的2-一致凸性系数;κ是E*的2-一致光滑系数.设n:=n+1返回步骤1. 下面给出算法的强收敛性. 引理2.1若假设1成立,xn,yn,λn是算法A产生的序列,则有下面的成立: (1)对于某个n∈N,如果xn=yn,那么xn∈S; 证明(1)如果xn=yn,又由xn=ΠCJ-1(Jxn-λnAxn),所以xn∈C.由引理1.3(i),有 〈w-xn,Jxn-(Jxn-λnAxn)〉≥0,∀w∈C, 由上式可得到λn〈Axn,w-xn〉≥0,∀w∈C,因为λn>0,所以有xn∈S. (2)显然{λn}是一个递减序列.因为A是L-Lipschitz连续映射且L>0, 若‖Axn-Ayn‖>0,有 引理2.2若假设1成立,{xn}是由算法A产生的序列,并且αn⊂(0,1).那么序列{xn}是有界的. 证明令x*∈S.由φ的定义,得到 φ(x*,wn)=φ(x*,J-1(Jyn-λn(Ayn-Axn))) =‖x*‖2-2〈x*,JJ-1(Jyn-λn(Ayn-Axn)〉+‖J-1(Jyn-λn(Ayn-Axn))‖2 =‖x*‖2-2〈x*,Jyn-λn(Ayn-Axn)〉+‖Jyn-λn(Ayn-Axn)‖2 =‖x*‖2-2〈x*,Jyn〉+2λn〈x*,Ayn-Axn〉+‖Jyn-λn(Ayn-Axn)‖2. (7) 利用引理1.2,可得到E*是2-一致光滑的,再利用引理1.3,则得到 ‖Jyn-λn(Ayn-Axn)‖2≤‖Jyn‖2-2〈yn,λn(Ayn-Axn)〉+2κ2‖λn(Ayn-Axn)‖2. (8) 将(8)带入(7),可得到 φ(x*,wn)≤‖x*‖2-2〈x*,Jyn〉+2λn〈x*,Ayn-Axn〉+‖Jyn‖2-2λn〈yn,Ayn-Axn〉 +2κ2‖λn(Ayn-Axn)‖2=φ(x*,yn)-2λn〈yn-x*,Ayn-Axn〉 +2κ2‖λn(Ayn-Axn)‖2. (9) 利用引理1.4(i),得到 φ(x*,yn)=φ(x*,xn)+φ(xn,yn)+2〈x*-xn,Jxn-Jyn〉 =φ(x*,xn)+φ(xn,yn)+2〈xn-x*,Jyn-Jxn〉. (10) 将(10)带进(9),可得到 φ(x*,wn)≤φ(x*,xn)+φ(xn,yn)+2〈xn-x*,Jyn-Jxn〉-2λn〈yn-x*,Ayn-Axn〉 +2κ2‖λn(Ayn-Axn)‖2=φ(x*,xn)+φ(xn,yn)-2〈yn-xn,Jyn-Jxn〉 +2〈yn-x*,Jyn-Jxn〉-2λn〈yn-x*,Ayn-Axn〉 +2κ2‖λn(Ayn-Axn)‖2. (11) 利用引理1.4(ii),则得到: -φ(yn,xn)+2〈yn-xn,Jyn-Jxn〉=φ(xn,yn) (12) 结合(11)和(12),得到 φ(x*,wn)≤φ(x*,xn)-φ(yn,xn)+2〈yn-x*,Jyn-Jxn〉 -2λn〈yn-x*,Ayn-Axn〉+2κ2‖λn(Ayn-Axn)‖2. (13) 利用引理1.5(i),得到〈Jxn-λnAxn-Jyn,x*-yn〉≤0,因为x*∈C,这就意味着 〈Jyn-Jxn+λnAxn,yn-x*〉≤0,这就等价于 〈Jyn-Jxn,yn-x*〉≤-λn〈Axn,yn-x*〉. (14) 将(14)带入(13),则得到: φ(x*,wn)≤φ(x*,xn)-φ(yn,xn)-2λn〈Axn,yn-x*〉-2λn〈Ayn-Axn,yn-x*〉 +2κ2‖λn(Ayn-Axn)‖2=φ(x*,xn)-φ(yn,xn)-2λn〈Ayn,yn-x*〉 +2κ2‖λn(Ayn-Axn)‖2≤φ(x*,xn)-φ(yn,xn)+2κ2‖λn(Ayn-Axn)‖2 -2λn〈Ayn-Ax*,yn-x*〉-2λn〈Ax*,yn-x*〉. (15) 因为A是单调的且x*∈S,所以可得到〈Ayn-Ax*,yn-x*〉≥0和〈Ax*,yn-x*〉≥0,从(15)中有: φ(x*,wn)≤φ(x*,xn)-φ(yn,xn)+2κ2‖λn(Ayn-Axn)‖2 (16) (17) 利用xn+1的定义,对每个n>N0,有: φ(x*,xn+1)=φ(x*,J-1(αnJx1+(1-αn)Jwn))=‖x*‖2-2〈x*,JJ-1(αnJx1+(1-αn)Jwn)〉 +‖J-1(αnJx1+(1-αn)Jwn)‖2=‖x*‖2-2〈x*,αnJx1 +(1-αn)Jwn〉+‖αnJx1+(1-αn)Jwn‖2≤‖x*‖2 -2αn〈x*,Jx1〉-2(1-αn)〈x*,Jwn〉+αn‖Jx1‖2+(1-αn)‖Jwn‖2 =αn‖x*‖2-2αn〈x*,Jx1〉+αn‖Jx1‖2+(1-αn)‖x*‖2 -2(1-αn)〈x*,Jwn〉+(1-αn)‖Jwn‖2=αnφ(x*,x1)+(1-αn)φ(x*,wn) =αnφ(x*,x1)+(1-αn)φ(x*,xn)≤max{φ(x*,x1),φ(x*,xn)} ≤··· ≤max{φ(x*,x1),φ(x*,x1)}=φ(x*,x1). (18) 所以{φ(xn,x*)}有界,则有{xn}有界. 引理2.3若{xn},{yn}是由算法A产生的序列,假设‖xn-yn‖→0,n→∞,p∈C是{xnk}的弱极限,这里k⊆N,那么有p∈S. 证明对任意的x∈C,利用引理1.5(i),则有(因为A是单调的) 0≤〈Jynk-Jxnk+λnkAxnk,x-ynk〉 =〈Jynk-Jxnk,x-ynk〉+λnk〈Axnk,xnk-ynk〉+λnk〈Axnk,x-xnk〉 ≤〈Jynk-Jxnk,x-ynk〉+λnk〈Axnk,xnk-ynk〉+λnk〈Ax,x-xnk〉 通过取极限,得到〈Ax,x-p〉≥0,∀x∈C,利用引理1.9得到p∈S. 现在证明本文算法的强收敛性. 证明利用引理2.2,可知道{xn}有界,又由引理1.5(iii)则有 φ(z,xn+1)=φ(z,J-1(αnJx1+(1-αn)Jwn)) =V(z,αnJx1+(1-αn)Jwn) ≤V(z,αnJx1+(1-αn)Jwn-αn(Jx1-Jz))+2αn〈Jx1-Jz,xn+1-z〉 =V(z,αnJz+(1-αn)Jwn)+2αn〈Jx1-Jz,xn+1-z〉 ≤αnV(z,Jz)+(1-αn)V(z,Jwn)+2αn〈Jx1-Jz,xn+1-z〉 =(1-αn)V(z,Jwn)+2αn〈Jx1-Jz,xn+1-z〉 ≤(1-αn)V(z,Jxn)+2αn〈Jx1-Jz,xn+1-z〉 =(1-αn)φ(z,xn)+2αn〈Jx1-Jz,xn+1-z〉. (19) 为了得到算法A的强收敛性,设an:=φ(z,xn)并且将证明分成两个部分,如下: φ(z,xn+1)≤αnφ(z,x1)+(1-αn)φ(z,wn) (20) 又因为‖xn-yn‖→0,n→∞,所以从wn的定义可以得到: 这里M2>0,所以有‖wn-yn‖→0,n→∞.此外由xn+1的定义得到: ‖Jxn+1-Jwn‖=αn‖Jx1-Jwn‖≤αnM3→0(n→∞), (21) 这里M3>0,因为J-1在E*的有界子集上是范数到范数一致连续的,所以可以得到‖xn+1-wn‖→0,n→∞. 所以有‖xn+1-xn‖≤‖xn+1-wn‖+‖wn-yn‖+‖yn-xn‖→0,n→∞,因为{xn}有界,所以我们可以选择 {xn}的一个子序列{xnk},使得{xnk}弱极限是p∈E,并且有: 因为z=ΠCx1,所以有: (22) 因此xn→z,n→∞. φ(z,xnk)≤φ(z,xnk+1)andφ(z,xk)≤φ(z,xnk+1). (23) 通过观察,得到: φ(z,xnk)≤φ(z,xnk+1)≤αnkφ(z,x1)+(1-αnk)φ(z,wnk)≤αnkφ(z,x1)+(1-αnk)φ(z,xnk). xn→z,n→∞.‖xnk-ynk‖→0,k→∞,‖ynk-wnk‖→0,k→∞,‖xnk+1-xnk‖→0,k→∞. 类似地,可以推出: (24) 从(19)和(20)得到: φ(z,xnk+1)≤(1-αnk)φ(z,xnk)+2αnk〈Jx1-Jz,xnk+1-z〉 ≤(1-αnk)φ(z,xnk+1)+2αnk〈Jx1-Jz,xnk+1-z〉. 因为αnk>0,所以有φ(z,xnk)≤φ(z,xnk+1)≤2〈Jx1-Jz,xnk+1-z〉,由(24)则有: 因此xk→z,k→∞.即证.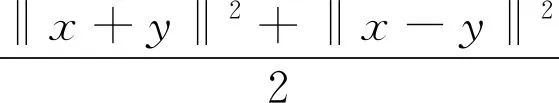
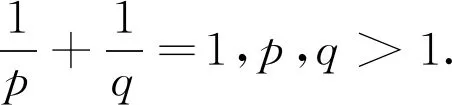

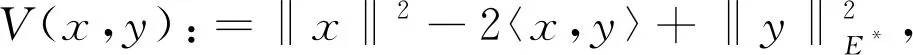
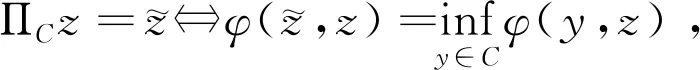
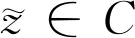
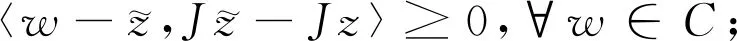

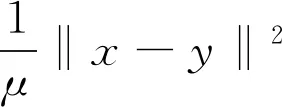
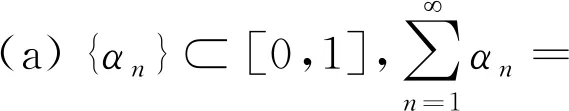
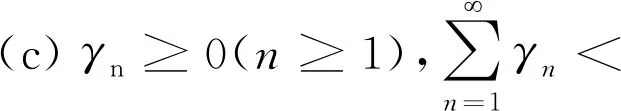
2 结果