“四招”破解含参不等式恒成立问题
2022-03-07谢志坚谢梅林
语数外学习·高中版上旬 2022年1期
谢志坚 谢梅林
含参不等式恒成立问题的综合性较强,常与不等式、方程、三角函数、解析几何、向量等知识相结合,侧重于考查同学们的逻辑思维能力和运算能力.含参不等式中含有参数,导致题目的难度增加,很多同学在解题时经常出现束手无策的情况.对此,笔者总结出解答含参不等式恒成立问题的四个“妙招”,供大家参考.
一、采用判别式法
判别式法通常用于求解含参二次不等式恒成立问题.在解題时,首先要判断二次不等式的二次项系数是否为0.若为0,需将不等式看作一次不等式进行讨论;若不为0,需将不等式构造成一元二次方程,根据根的分布情况,讨论一元二次方程的判别式是大于0、等于0还是小于0;最后通过计算得出结论.

该二次不等式的二次项系数中含有参数,因此需分系数为0或不为0两种情况进行讨论.值得注意的是,只有在二次项系数不为0时,才可运用判别式法解题.
二、分离参数
有些不等式中的参数容易被分离出来,此时,我们可以采用分离常数法来求解不等式恒成立问题.首先将含参不等式进行变形,把参数分离出来,使不等式的一端只含有参数,另一端不含有参数,然后将不含有参数的式子构造成函数式,通过研究函数的性质或者导函数的性质求得函数的最值,建立使不等式恒成立的关系式,便可求得问题的答案.



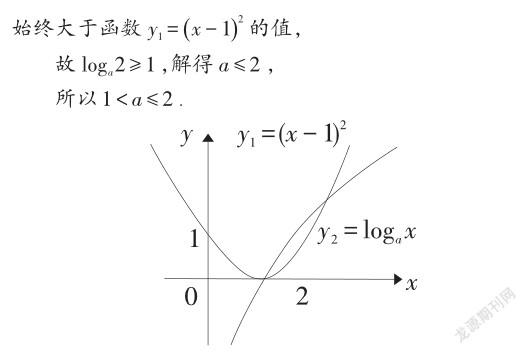
我们根据不等式的特点构造两个函数:二次函数和指数函数,其图象分别为抛物线的一部分和对数函数的图象.采用数形结合法,通过分析图象的位置关系,即可求出a的取值范围.
虽然含参数不等式恒成立问题形式多变且解法众多,但是我们只要抓住解题的关键,将不等式进行适当的变形,构造出一元二次方程、分离参数、变更主元、将数形结合,便能将问题转化为方程、函数、图形问题来求解,快速破解难题.
(作者单位:江西省赣州市南康区第三中学)
