2021年高考概率与统计试题的统计与分析
2022-03-07胡茗洁石浩楠胡典顺
胡茗洁 石浩楠 胡典顺



【摘要】概率与统计是高中数学课程的主线,也是高考数学的主要考查内容.以2021年高考数学新高考Ⅰ卷、新高考Ⅱ卷、全国甲卷理科等八套试卷中“概率与统计”相关试题为研究对象,从情境类型、知识点、数学核心素养、关键能力、综合难度五个维度对其进行特点分析.发现,2021年高考数学“概率与统计”试题具有情境类型丰富、讲究知识的应用性与综合性、融合多种核心素养与关键能力的特点,在难度上不同试题在难度因素的侧重上各有不同,大部分试题强调运算难度.对教师的概率与统计教学和高考试题的命制提出以下几点建议:丰富问题情境,培养关键能力;注重知识整合,建构完整体系;回归知识本质,落实核心素养;合理设置难度,优化试卷质量.
【关键词】高考数学;概率与统计;试题分析
1问题提出
随着大数据时代的到来,概率与统计的基础知识已经成为一个未来公民所必须具备的常識.在高中数学课程中,概率统计是一个重要主题,贯穿必修、选择性必修和选修课程.解决概率与统计相关问题需要经历问题情境的数学化、模型的建构、数据分析、数学运算、还原为现实问题的解等步骤[1],是培养学生数学核心素养、发展应用意识的重要媒介.
近年来,高考对统计与概率的考查出现了新的趋势:注重基本概念的理解与应用,试题情境更加真实和复杂,模型更加精细和完善[2].这不仅为教师的教学指明了方向,也对学生的学习提出了更多新的要求.故本文对2021年高考数学中的概率与统计试题进行分析,以期更清楚地把握高考的考核方向,为教师的教学提供思路,也为高考试题的命制提供参考.
2分析框架
本文以新高考Ⅰ卷、新高考Ⅱ卷、全国甲卷理科、全国乙卷理科、北京卷、上海卷、浙江卷、天津卷共八套试卷为研究对象,从情境类型、知识点、数学核心素养、关键能力、综合难度五个维度出发对概率统计相关试题进行统计与剖析,并归纳得出2021年高考数学概率与统计试题的命制特点.在统计编码过程中,统计结果经过与相关专家与团队成员多次讨论后确定,以尽可能保证统计的准确性与全面性.
2.1情境类型
概率是研究随机现象的强有力工具,统计通过收集、分析数据解决实际生活中的问题,概率与统计已经渗透到现实生活的方方面面[3].基于概率与统计内容领域的特色,高考对此部分的考查一直坚持与情境相联系,本文参考《普通高中数学课程标准(2017年版2020年修订)》(以下简称“课标”)中对情境与问题的解释,将情境划分为现实情境、数学情境、科学情境三个维度.
2.2知识点
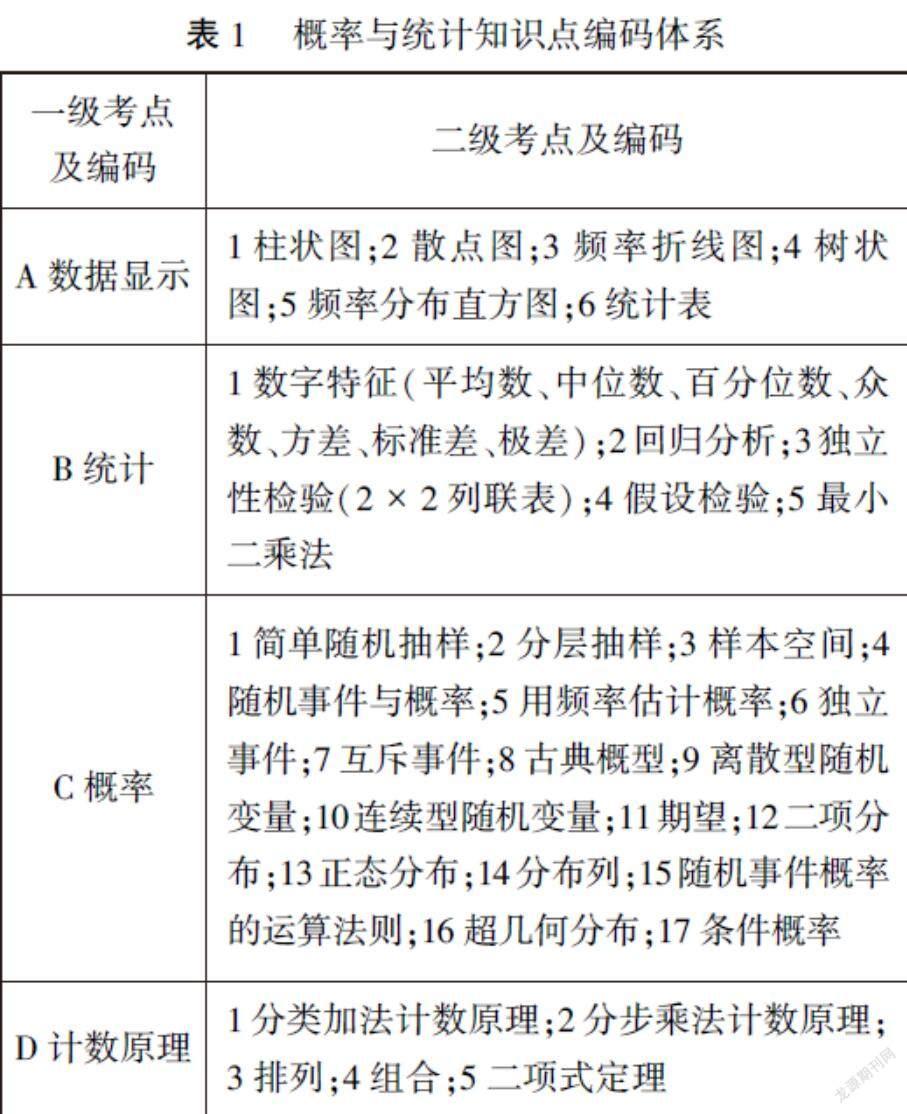
明晰考查内容领域的知识点,有利于教师和学生把握核心知识点,更好地应对高考的挑战.本文参考课标中对知识点的划分,选取其中“概率与统计”内容,结合试题实际情况,得到概率与统计的知识点编码框架,具体内容见表1.
如表1所示,一级考点用字母表示,二级考点用数字表示.如,A2表示散点图,B2表示回归分析.试题中涉及的其他领域的知识点,由于不是主要内容,不做一一编码,遇到时直接列出即可.
2.3数学核心素养
作为课标的一大亮点,数学核心素养渗透在几乎所有的数学知识、技能中,是学生在接受教育过程中逐步形成的具备数学本质特征而且适应个人终身发展和社会发展需要的关键能力与思维品质[4].在概率统计的学习中,学生需要经历数据统计的全过程,多种素养均能得到发展,本文参照课标中提出的六大数学核心素养——数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析[8]进行试题的统计与分析.
2.4关键能力
关键能力作为“一核四层四翼”中“四层”的一环,指学生在生活实践中或探索问题情境时,应用知识有效地认识问题、分析问题、解决问题的能力[3],是高中数学课程的培养目标.高考数学通过情境承载考查内容,以实现考查要求,这与概率与统计特有的情境性不谋而合,因此,在概率与统计这一内容领域更容易培养学生的数学关键能力.本文依据高考评价体系将关键能力划分为逻辑思维能力、运算求解能力、空间想象能力、数学建模能力、创新能力五个维度.
2.5综合难度
试题难度是反映试题质量和测验公平性的一项重要指标.目前已有不少学者展开了对高考试题难度的研究,并形成了一些比较成熟的框架.本文综合武小鹏所搭建的综合难度模型框架[3],以及薛欢等在此基础上提出的针对于概率与统计试题的综合难度模型[4],对试题进行综合难度的分析,模型的具体因素及其等级如表2所示.
在表2中,利用di=∑jnijdijn计算各因素的难度系数di,其中i表示不同的因素,dij表示第i个因素中的第j个等级的权重(依据不同等级分别取1,2,3,…),nij表示这组题目中属于第i个因素中的第j个等级的题目个数,n代表题目的总个数.因此整套试题的综合难度系数就是各因素综合难度系数的加权平均,设ki为各因素在整个试题中所占的权重系数,那么整套试题的综合难度系数D=∑7i=1diki.关于权重系数的确定,参考武小鹏[6]研究中韩高考试题时提出的权重系数,即以“背景因素”权重为1.00作为参考标准,各因素所占权重依次为1.00,1.21,1.19,1.53,0.91,1.17,1.35.
3数据的统计与分析
根据分析框架,将所得结果分为两个部分分析:一部分呈现试题的命制特点,包括情境类型、知识点、核心素养和关键能力的分析;另一部分呈现综合难度系数的分析.
3.1试题命制特点分析
在进行统计分析时,根据题目的设问方式,将试题分为封闭型试题和开放型试题两类,封闭型试题包括选择题和填空题,开放型试题包括解答题.
(1)封闭型试题特点分析
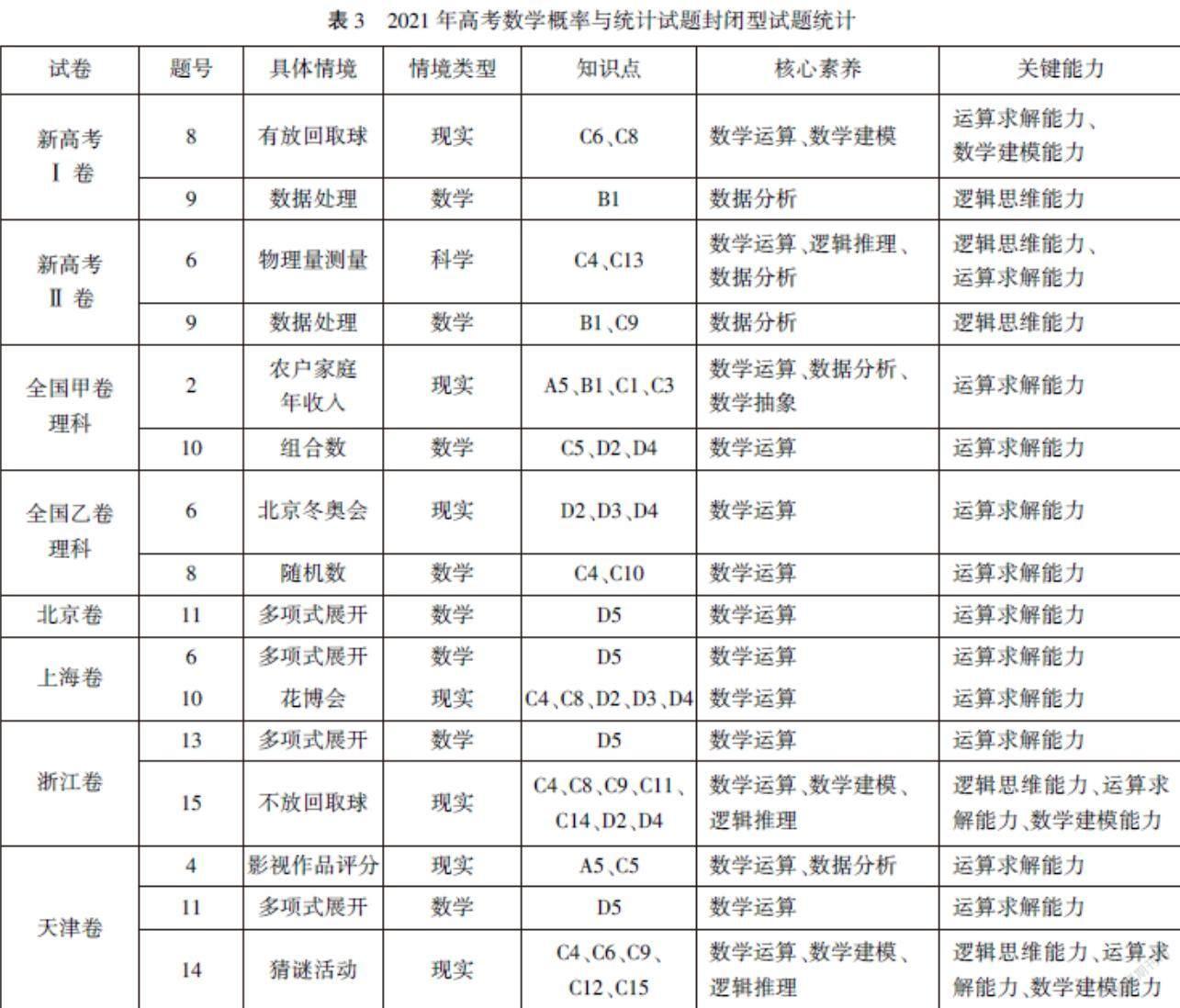
根据第二部分搭建的分析框架对2021年高考数学封闭型的概率与统计试题进行统计,具体内容如表3.
在情境类型方面,如图1所示,考查情境类型多样,以数学情境最多,现实情境次之,仅有新高考Ⅱ卷涉及科学情境的封闭型试题.从具体情境来看,高考充分体现了数学思政的要求,于问题情境中关注社会时事与经济发展.如全国甲卷理科第2题[6],“以我国在扶贫脱贫工作取得全面胜利和农村振兴为背景,通过图表给出某地农户家庭收入情况的抽样调查结果”,培养学生社会责任感,增强民族自豪感与国家意识.
在知识点的考查上,封闭型试题考查的知识点一般为1~3个,仅全国甲卷理科涉及4个知识点的封闭型试题.具体考查以概率为主干知识点,向外延伸,考查范围广,但与其他领域结合较少,符合概率与统计“广而不深”的特点,讲究知识的应用性与综合性.
对于核心素养,在“重视理性思维,坚持素养导向、能力为重的命题原则”[7]下,核心素养以数学运算为主,在强调简单运算的基础上,落实数学建模、数据分析等素养的考查,表明高考数学命题顺应时代特征,對概率与统计的实用性提出了要求,以便让学生更好地应对现实生活中的问题.
对于关键能力的考核,以运算求解能力居多,但在兼顾概率与统计领域特点的同时,尽可能多地考查了其他能力,合理科学地践行了高考评价体系,充分发挥了高考的选拔功能.
(2)开放型试题特点分析
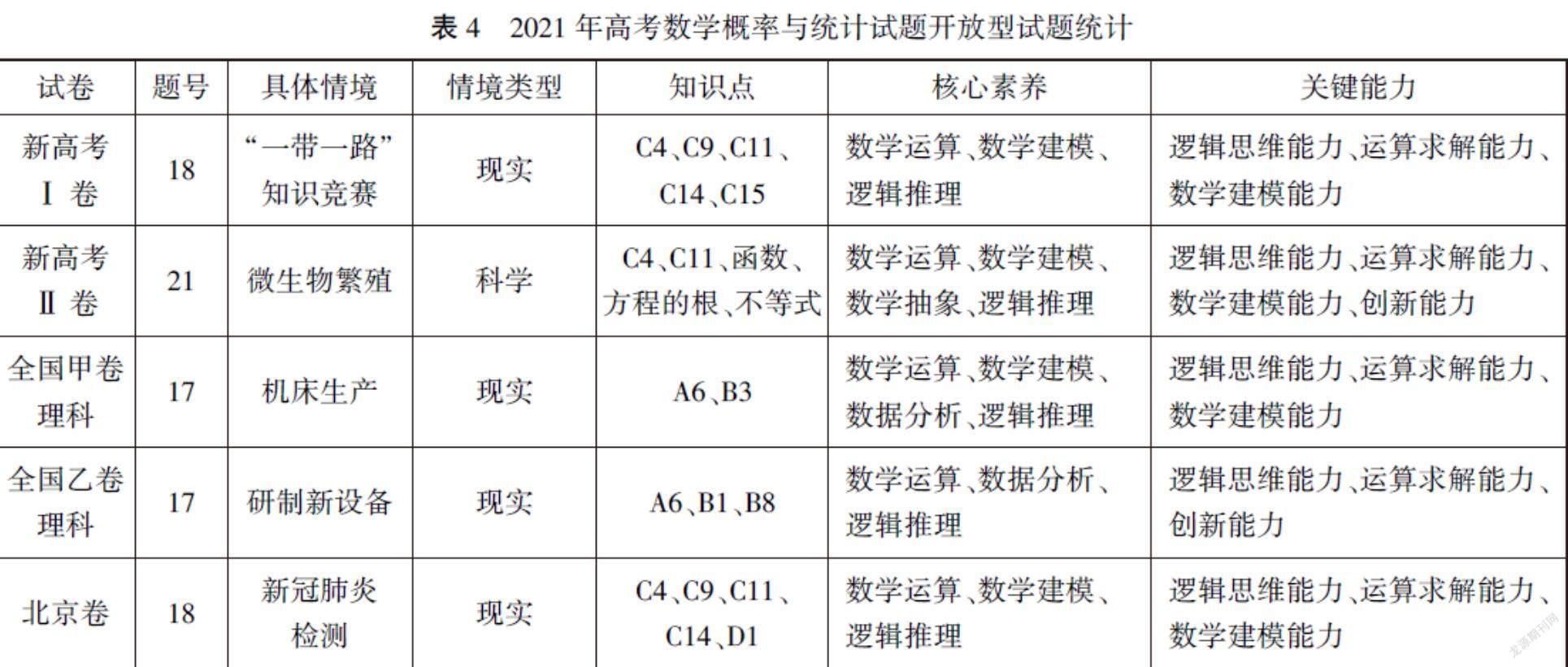
根据第二部分搭建的分析框架对2021年高考数学开放型的概率与统计试题进行统计,具体内容如表4.
在情境类型方面,开放型试题的问题情境以现实情境为主,含有少量的科学情境.具体情境的选择非常丰富,概括为如下三大特点:紧扣时事热点,培养学生的家国情怀,如新冠肺炎检测;贴近学生的日常生活,激发学生对数学学习的兴趣,如“一带一路”知识竞赛;与科技、生产相融合,培养学生的数学应用意识,如微生物繁殖、机床生产以及研制新设备.
在知识点的考查上,开放型试题所考查的知识点通常有3~5个,普遍多于封闭型试题,体现出开放型试题的综合性.大部分知识点归属于一级考点B和C之下,涉及其它领域数学知识的试题较少,仅有一题,几套试卷相比较而言,新高考Ⅱ卷所考查的知识点是最多的,而且存在跨章节学科知识的交叉.
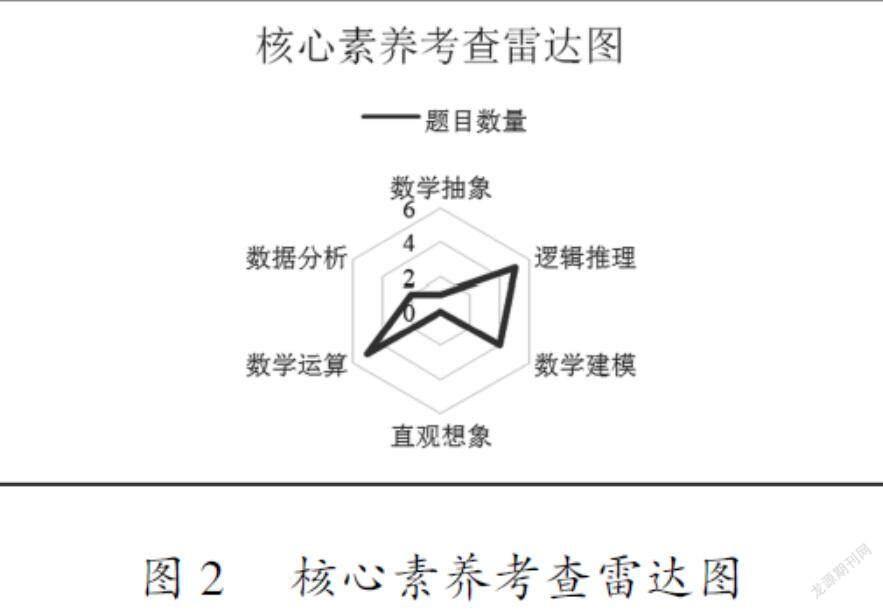
就核心素养而言,每道试题都考查了3~5种核心素养.根据每种核心素养所涉及的开放题数量,绘制雷达图,如图2所示.不难发现,概率与统计开放题侧重逻辑推理和数学运算的考查.以新高考Ⅱ卷第21题为例,学生需要从微生物的繁殖情境中抽象出概率之间的数学关系,并在此基础上建立模型进行期望的求解,最后通过逻辑推理加深对问题实际含义的理解.
对于关键能力,逻辑思维能力、运算求解能力、数学建模能力是大部分试题所涉及的,这与核心素养的考查相呼应.除此之外,少部分试题渗透了对于学生创新能力的培养,如全国乙卷第21题,重在考查学生思维的灵活性.
3.2试题综合难度分析
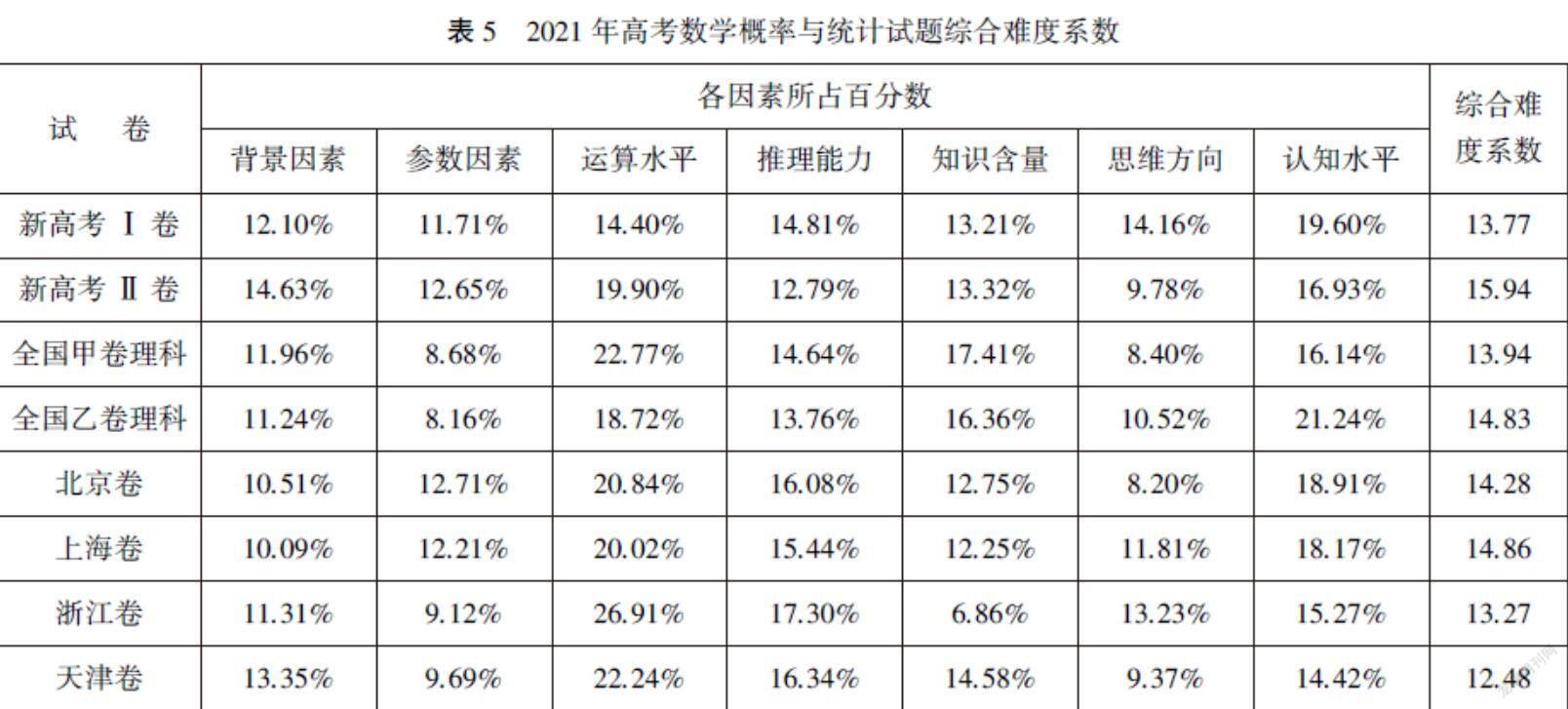
根据综合难度模型下的公式,计算各套试卷概率与统计相关试题的综合难度系数,如表5所示.
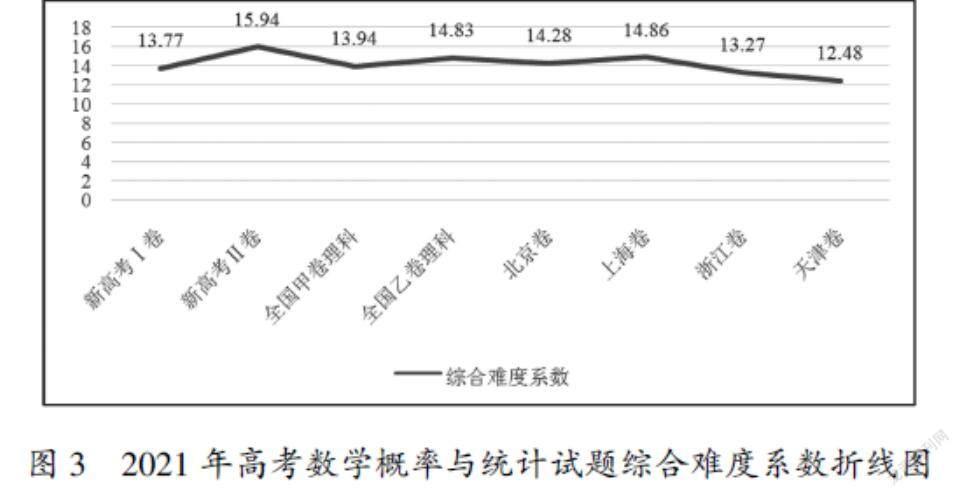
根据表5中的难度系数绘制折线图,如图3所示.
从宏观整体来看,新高考Ⅱ卷的概率与统计试题综合难度系数最高,天津卷的概率与统计试题综合难度系数最低,其他几套试卷概率与统计试题的综合难度不相上下.从微观细节来看,新高考Ⅰ卷认知水平因素贡献难度最多,其他分配较均匀,全国甲卷理科知识含量与认知水平并重,新高考Ⅱ卷和全国乙卷理科则是运算水平与认知水平并重,北京卷、上海卷、浙江卷、天津卷对运算水平要求较高,或在参数因素或在思维方向因素占比较低,各有特色.
仔细剖析综合难度系数的各难度因素,可以发现:在情境的选择上,新高考Ⅱ卷最为综合,具备一定的创新性;在运算水平上,浙江卷的要求最高,不少试题已经涉及到了符号运算,同时,浙江卷对推理能力的考查也是最复杂的;在知识点含量上,两套全国卷的知识点含量是最丰富的;在思维方向上,新高考Ⅰ卷和浙江卷两套试卷给予逆向思维更多的关注;对于试题所考查的认知水平,全国乙卷理科和新高考Ⅰ卷这两套使用地区较多的试卷要求学生不仅掌握知识并应用,还要能够进行一定的分析推理.
4启示与建议
4.1丰富问题情境,培养关键能力
创设合适的问题情境,既能有效提高试题质量,也更有利于落实“一核四层四翼”的高考评价体系.概率与统计的广泛应用性为高考试题中问题情境的创设提供了天然的优势,2021年高考数学概率与统计相关试题的情境设置以现实情境居多,尤其是开放题,都非常贴近日常生活,聚焦时事热点,突显出理论联系实际的导向.
在教学中,教师应注意情境创设的艺术,在教学中适当增加一些学生比较陌生的问题情境,为学生创新思维的培养提供探索的“黑箱”[8].在情境的设问方式上,要注意开放性,给予学生充分的思考空间,摆脱定势思维的束缚,使学生得到关键能力的综合发展.
4.2注重知识整合,建构完整体系
高考数学在考查过程中要体现综合性,这样有利于促进学生从整体上建构知识框架,形成合理的认知结构[9].概率与统计是高中数学知识点中的关键部分,与其他知识点有着明显的渗透交汇,也是高考的重难点.2021年高考数学概率统计试题不仅涵盖知识点丰富,而且已经有部分试题表现出函数、方程等跨章节甚至生物、科学等跨学科知识的交互,旨在培养学生融会贯通的意识.
在教学中,教师可以适当利用概念图、思维导图等知识表征工具帮学生梳理核心知识点,建构概率统计的知识体系.还应当及时地进行回顾复习,厘清概率统计与方程、函数、不等式等其它知识单元的联系,深化对数学概念的理解.除此之外,教师还可以利用探究性学习的模式介绍一些学科交叉的内容,积极探索多学科交叉融合的有效途径,以培养学生的创新意识.
4.3回归知识本质,落实核心素养
对数学知识本质的理解是学生发展数学核心素养的必要条件,高考试题不仅要考查学生对知识点的熟练程度,更应当突出知识的本质,引导学生从学科的视角理解世界和分析问题,概率统计的本质是随机性数学思维.今年高考数学中所涉及的古典概型、正态分布、几何概型等随机模型,皆是对现实随机问题的抽象凝炼,既体现了数学之美,又彰显了数学的实用性.
在教学中,教师应帮助学生转变固有的思维方式,激发自觉培养随机性数学思维的意识.在对典型题目进行剖析时,尽可能完整地展现推理过程,使学生积累一些常用模型,并且能灵活运用.通过对数学知识进行整体性的分析,梳理概率统计自身的逻辑关系,使得每一堂课都立足于概率统计的本质,聚焦其内核.
4.4合理设置难度,优化试卷质量
编制一套高质量的高考数学试题,最大的价值追求就是既要保证难度设计的科学合理又能检测出学生的真实水平,同时还要充分发挥高考数学试题的选拔功能和积极导向作用.今年不同试卷概率与统计的试题在各难度因素的分配上各不相同. 但总体来说,试卷在难度的设计上均应当依据课标对概率统计部分的要求,秉持发展学生的数学核心素养理念,从每个难度因素自身的特点出发,合理设置各难度因素,提高试卷的区分度.
在教学中,教师应当把握概率与统计的教学重点,除了要求学生掌握知识点之外,更要培养学生的核心素养与关键能力,通过给予学生更多的具有现实背景意义的案例,让学生体会数据分析的全过程,不断提高运算水平,从概念理解逐步走向灵活运用、独立分析.
参考文献
[1]廖艺捷,朱展霖,胡典顺.近五年高考概率与统计试题的统计与分析——以全国Ⅰ卷(理科)为例[J].数学通报,2021,60(02):5662.
[2]赵轩,任子朝.高考概率统计试题考查目标的沿革与实现[J].数学通报,2019,58(10):3943.
[3]中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[M].北京:人民教育出版社,2018.
[4]路江江,王亚妮.高中数学教育中如何培养学生的数学核心素养——王尚志教授访谈录[J].数学教育学报,2021,30(02):6770.
[3]李勇,赵静宇,史辰羲.高考评价体系的基本内涵与主要特征[J].中国考试,2019(12):712.
[4]武小鹏,孔企平.基于AHP理论的数学高考试题综合难度模型构建与应用[J].数学教育学报,2020,29(02):2934.
[5][14]薛欢,杜剑南,路江江.2016—2020 年高考数学(理科)全国卷“统计与概率”试题探析——基于综合难度模型[J].教育测量与评价,2020(12):3040.
[6]武小鹏,张怡.中国和韩国高考数学试题综合难度比较研究[J].数学教育学报,2018,27(03):1924+29.
[7][10]教育部考试中心.聚焦核心素养考查关键能力——2021年高考数学全国卷试题评析[J].中国考试,2021(07):7076.
[8]李健,童莉.高考评价体系中“应用性”与“创新性”要求——基于2020年高考数学试卷中问题情境的分析[J].基础教育课程,2020(Z2):1822.
[9]于涵,任子朝,陈昂,赵轩,李勇.新高考数学科考核目标与考查要求研究[J].课程·教材·教法,2018,38(06):2126.
作者简介胡茗洁(1998—),女,湖北宜昌人,华中师范大学数学与统计学学院研究生;研究方向数学课程与数学教学.
石浩楠(1999—),女,湖北十堰人,华中师范大学数学与统计学学院研究生;研究方向数学课程与数学教学.
胡典顺(1965—),男,湖北孝感人,华中师范大学数学与统计学学院教授、博士生导师;研究方向数学课程与數学教学.
