高等数学的演示程序设计
2022-03-05刘亚茹温桂敏王志鹏
刘亚茹 温桂敏 王志鹏
(南阳师范学院物理与电子工程学院 河南·南阳 473061)
0 引言
高等数学是理、工科院校一门重要的基础学科[1-2]。作为一门基础科学,高等数学有抽象性、逻辑性和应用性等特点。MATLAB(MatrixLaboratory)是 MathWorks公司推出的用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境的商业数学软件。MATLAB具有数值分析、数值和符号计算、工程与科学绘图、数字图像处理等功能。利用MATLAB软件,将导函数理论与实验演示设计相结合,我们可以更直观的去观察到函数的过程及结果,并且增强了同学对高等数学的理解力,丰富多彩的图像显示吸引了同学们的眼球,简单易便的过程提高了同学们的兴趣。
1 系统总体结构
关于高等数学的演示程序设计方面[3],我们可以划分为许多个不同的模块,例如一元微积分,二元微积分,空间几何,函数拟合及多元函数等多方面[4]。每个模块又可以划分为多个子模块。本演示系统框图如下所示。

图1:系统总体结构框图
2 子模块介绍
该演示系统包含的模块很多,这里只以“函数图像绘制”,“函数微积分”和“函数的曲线拟合”这三个模块为例来进行介绍。
2.1 函数图像绘制子模块
在高等数学中,画出函数的图像更有助于我们去观察到函数的变化[4],更方便我们对函数进行计算,直观地显示出结果,若我们直接徒手画则比较浪费时间,函数是复杂多变的,我们借助MATLAB来绘制图像,只要点击按钮,就可以根据在可编辑文本框中输入的函数参数的取值,绘制出相应的函数曲线,快速且直观。
2.2 函数微积分子模块
函数微积分有广泛的应用,例如在物理学、计算机学与电气学等上使用,并且经常用于几何计算、力学分析、电子信息计算中。
传统的数学方式不能直观显示图形,在计算复杂时,我们需要经过一系列的分析,分割、叠加,求导才能完成计算。所以运用程序演示,可以直接通过直接改变GUI或程序中的数值,来达到所求函数微积值,还可以直接观察到图形的函数图像,来得到我们想要的结果,可得问题的整体规律。
函数微积分子模块的界面如图2所示。该模块包含11个静态文本框,9个可编辑文本框,3个普通按钮和1个下拉按钮。其中,静态文本框用于标注信息提示,可编辑文本框用来获取函数的微积分区域与最值。并且按下普通按钮的任意一钮,我们都可通过坐标轴来展示函数的曲线,这让我们更生动形象地了解此函数的求导结果及积分结果;我们可在下拉按钮来获取不同的颜色来绘制曲线。

图2:函数微积分子模块
2.3 函数的曲线拟合子模块
多项式曲线拟合,就是在众多的样本点中进行拟合,找出满足样本点分布的多项式。其主要功能为在众多采样点中,找出直线上离采样点最近的点,称为预测点,而这条曲线就是我们所拟合出来的直线,而预测点与采样点之间的点称为误差,假设有一个直线y=ax。针对这个误差,使用误差平方和来表示:,因此我们需要这个误差和平方达到最小,来达到所求目的。
函数曲线拟合子模块的界面如图3所示。按下按键,可以显示出插值曲线和实际曲线,其中,建立两个静态文本框,输入相应的控件名称。其次建立一个动态文本框,用于输入拟合的次数。再者包括三个下拉菜单分别用于选择图形的线型,颜色及粗细。此外建立了一个复选框,选择用于不同方式拟合。最后建立了三个按钮,分别用于多项式拟合、差值拟合及最终的退出整个系统。
其GUI用户界面图形设计结果如下:
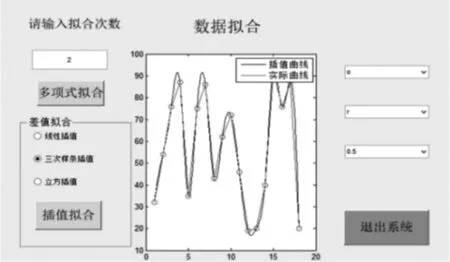
图3:函数曲线拟合子模块
3 总结
本文通过用GUI仿真对函数图像的描述、导数和积分,方便学生深刻理解高数中的某些概念,掌握其中的几何意义。让复杂的、抽象的、难以想象的问题及图形、难以绘制的函数转化为可视化GUI界面,使图像更生动形象、让人简单明了,降低了高数的学习难度,激发同学们对高数的求知欲。
