面向师范生的高等代数课程的若干概念教学探讨
2022-03-05张迪
张 迪
(广东第二师范学院数学学院 广东·广州 510303)
面对新的教育理念和新课程改革的要求,根本的策略是促进教师的专业化发展,而数学教师专业素质的培养和提升是其中的核心问题。
数学教师专业素质是在一般素质基础上形成和发展起来的数学教师职业的素养和品质,包括数学素养和品质,数学教育教学理论素养和品质以及数学教学技能。在数学师范生的培养方案中,一般通过数学学科基础课群,数学专业课群,教育学及心理学基础课群,数学教育课群来实现培养目标。
数学教学技能是数学教师以教学操作知识为基础的心智技能与动作技能的统一。动作技能包括一系列外部可见的肢体动作,如语音,语调,语速,板书等,还包括口语表达技能,书面表达技能等部分。心智技能则主要指教师基于自身的数学素养及数学教学素养完成的心智活动方式,包括讲解,提问,抽象概括等等。从对数学教学技能结构的剖析不难发现,教师的数学教学技能首先是教师基于个人数学素养,数学教育教学素养的外显行为方式,是教师实现个人相关素质的外显,传递和迁移的工具。
目前在师范生的培养中,“重视动作技能,轻视数学思想内化,轻视数学素养内化”的现象是普遍存在的,学生的“心智技能”的形成相对滞后。这与师范生培养过程中,数学学科知识学习,数学教育教学理论学习与教学技能培养三方面被割裂有关系,也与高校教师和学生本人的意识有关。
笔者从事师范生的教育工作,因此比较关注中小学数学教育教学。在中小学,常有老师们不能确定一道题的计算过程或者结果对错于否,笔者认为造成这一现象的原因是教师对于教材中概念的理解和把握不够准确造成的。要杜绝此类事件的发生,需要授课教师对概念有深刻的认识,包括对数学概念的来龙去脉的掌握,对概念内涵的理解,概念外延的把握,以及清楚数学概念在中小学中的界定与表述(中小学数学教材由于受学生思维水平的限制,有的数学概念会采用不严格的描述性代替[2])等。除了上面的问题,在数学师范生试讲、实习时还会反映出其他一些问题,比如学生对数学的书面表达,口头表达不够严谨;对数学的理解孤立片面,不能很好的将知识联系起来,缺乏对知识的宏观把握;不太懂数学推理和数学方法,导致不能够意识到中小学的一些规律和计算法则是通过归纳和推理得到的,因而不能够在课堂讲授中体现出来等等。数学学科知识是数学教师专业成长的一个重要方面,数学教师只有具备了精深的数学专业知识,教学技能才能有效的发挥作用,才能更好的灵活变通,教师才有可能成为教学的真正能手,否则只能照本宣科或者耍耍空架子[3]。
本文通过高等代数中的几个课题特别是概念课题,进行加强和培养学生对数学学科知识与思想方法的学习与体会的案例分析,为师范生“心智技能”的养成提供支持。
1 数学概念
数学概念是反映现实世界空间形式与数量关系本质属性的思维形式[1]。数学的理论,小到一篇论文,大到专著,都是由数学概念,数学事实,数学方法(这是一切数学材料的基本要素)[5]构成的。数学事实是概念的内涵,数学方法用来组建从“概念”里挖掘“事实”的途径。因此,数学概念在数学理论体系中最基本也最重要。
2 高等代数中的若干概念课题探讨
2.1 关于多项式的一些概念的讲授
我们的课程教材选用了张禾瑞,郝鈵新编的《高等代数》第五版。
2.1.1 多项式的整除


这个概念的上述处理是让学生体会数学理论体系一切从定义出发,一切以定义为依据。
2.1.2 多项式的分解


2.2 关于线性变换的一个概念和事实的讲授
线性变换是高等代数的核心内容之一,它与向量空间,矩阵,向量空间的基,向量,坐标,特征值,特征向量,正交变换,对称变换等都有密切联系,是学习的重点和难点之一。笔者在这部分内容的讲授中常使用关系图,以及数形结合的方法。这可以帮助学生对知识形成一个整体的认知,相对轻松的理解知识。既可以提高学生的学习兴趣和积极性,也能让他们看到数形结合的好处。下面考察一个具体案例。
教材在引入线性变换关于给定基的矩阵概念后,给出一个定理[6]:

我们画图理解如下(图中字母的含义见定理):

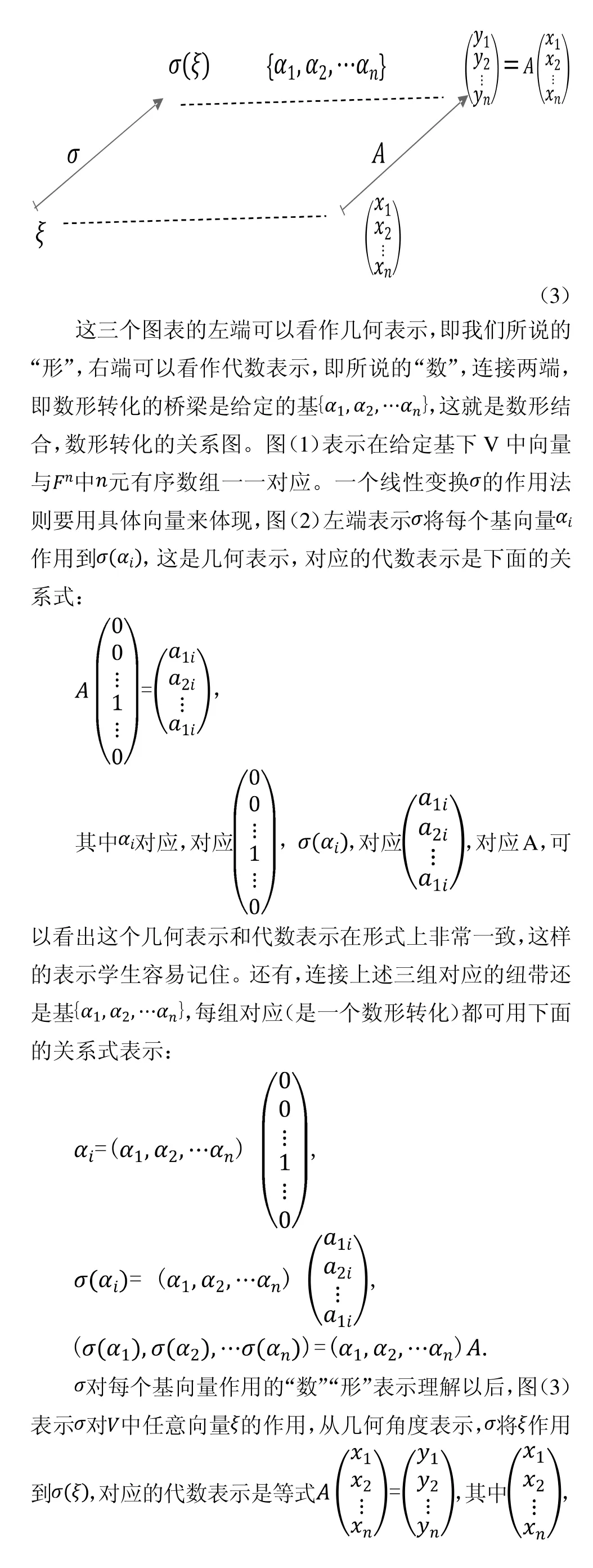

用关系图去理解定理,它的结论自然而然,显而易见。学生容易理解定理,理清各个概念之间的关系,在遇到相关的习题时,就能够以不变应万变,应付各种题目。通过数形结合,数形转化,我们可以更好地理解数学概念和数学事实,抓住它的本质。
3 结论与思考
本文结合师范类本科院校的培养目标,在教学大纲的基本要求下,基于对师范生数学素养的培养和后续发展的考虑,对《高等代数》的概念课题的教学做了一些探索。
(1)数学学科知识学习,数学教育教学理论学习与教学技能培养三方面是不能被割裂开的,教师在课堂教学过程中除了让学生掌握基本知识、基本理论和基本方法外,也要注意培养他们用文字语言和数学语言准确的描述数学问题的能力和严谨认真的态度。
(2)在课堂讲授过程中,教师对教材要做适当的加工。在讲授概念时,要用各种图,表,注释,说明或者例子让学生理解定义字里行间背后隐藏的本质,要给学生展示如何把握概念。要让学生学着去理解概念而不是背诵它。要引导学生转变学习方法,培养学生的理解能力。
(3)在课堂上教师应该注重以学生为中心,多引导学生参与课堂,教师要多采用启发式教学,精心设计一些提问,比如在给出数学概念之前,用问题启发学生去思考如何用数学的语言描述事物;或者让学生参与讨论,自己概括出概念的本质特征;也可以在给出概念后,让学生提出一些和概念有关的问题。通过这样的方式可以调动学生的积极性,培养学生的创新能力。
(4)要培养学生对高等代数,对数学的兴趣。对于大多数师范生来说,他们以后的工作岗位是中小学老师,如果他们自身对数学,对数学的学习都没有兴趣,那么他们也不可能培养下一代学生对数学建立正确的观念。因此大学老师要通过各种方法,比如数形结合的方法,比如举例子的方法,让数学概念,数学事实变得容易理解,只有听得懂,学生才会有兴趣;还有在高等代数课堂上穿插数学史,名人轶事,代数在现代社会的广泛用途等,增加课堂趣味性,激发学生学习兴趣;还可以让学生了解高等代数与中小学数学的关系,比如高等代数里多项式,线性方程组的理论更加抽象和广泛,而中学的相关内容只是这些抽象内容的一个具体例子,解决这些抽象问题的思路方法完全可以用来指导和解决中学的相关题目,学生看到高等代数对中小学数学的作用,他们才能体会高等代数的重要性,从而重视这门课的学习。
(5)高等代数概念多且较为抽象,在课堂中要注意引导学生转变学习方法,转变学习观念,体会大学数学学习与中学数学学习的不同。一方面,要让学生在学习过程中注重知识本质的学习,而不是忙于做题;要理解数学,而不是记忆数学,模仿解题。另一方面,要在课堂教学中重视和渗透数学思想以及学习数学的方法,培养学生的数学观。
