基于PSR-PSO-RBF的短时交通流预测方法

徐新平 刘青意

(1.中交第二公路勘察设计研究院有限公司 武汉 430050; 2.中冶南方城市建设工程技术有限公司 武汉 430223)

高精度的短时交通流预测方法能准确预测交通流，城市道路管理部门可以依据预测结果实时制定相应的交通控制策略，提高城市道路通行效率。由于短时交通流具有明显的非线性特征[1]，而(radial basis function，RBF)神经网络[2]具有识别复杂非线性系统的特性，学者将其应用于短时交通流预测领域[3]，但是它存在初始权值和阈值不能准确获得的缺陷，导致预测精度有所欠缺[4]。为提高RBF神经网络模型对短时交通流的预测精度，黄文明等[5]利用人工蜂群算法优化RBF神经网络建立了短时交通流预测模型。考虑交通流的混沌特征，引入混沌交通流理论以提高交通流预测精度，刘立军等[6]提出了一种基于RBF神经网络和混沌理论的短时交通流预测模型。与传统RBF神经网络预测模型相比，上述方法虽然在一定程度上能提高短时交通流预测的精度，但是多采用优化算法对RBF神经网络的参数进行寻优或仅考虑交通流的混沌特征，甚少将二者结合起来统筹考虑RBF神经网络存在的缺陷和短时交通流的混沌特性，可能导致目前短时交通流预测方法的预测精度不高，无法更好地满足城市道路智能交通控制和管理的客观需求。

基于此，本文提出一种基于相空间重构(phase space reconstruction，PSR)和粒子群算法(particle swarm optimization，PSO)-RBF的短时交通流预测方法(PSR-PSO-RBF方法)，切实提高短时交通流预测精度，以满足智能交通控制和管理的客观需求。其中，考虑到短时交通流的混沌时间序列特征，相空间重构技术用于构建一种基于相空间的短时交通流时间序列：PSO算法旨在对RBF神经网络的输出权重、隐单元中心和宽度等关键参数取值进行寻优，克服其缺陷与不足；RBF神经网络模型主要用于对短时交通流进行预测。最后，以某道路交叉口的短时交通流为例，对比分析文中所提方法的有效性。

1 基于相空间的短时交通流时间序列重构技术

短时交通流具有混沌时间序列特性，相空间重构理论是混沌时间序列预测的基础，其基本原理是Takens等[7]提出的延迟嵌入定理，该定理认为选取适当的嵌入维数m和延迟时间τ，重构的m维状态相空间与系统原始状态变量构成的相空间是基本等价的，即重构的相空间内包含系统全部状态变量的演化信息，并根据该演化规律确定系统下一时刻状态，从而得到时间序列下一时刻的预测值。因此，通过实际交通流，采用基于相空间的短时交通流时间序列重构技术可以对具有混沌时间序列特性的短时交通流进行预测。

(1)

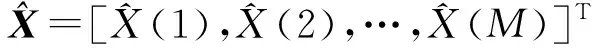
(2)

2 基于PSR-PSO-RBF的短时交通流预测方法

RBF神经网络是一种应用较为广泛的典型预测模型，它由输入层、隐含层和输出层3层组成。本文通过构建短时交通流3层前向RBF神经网络，来预测短时交通流，该前向RBF神经网络结构见图1。

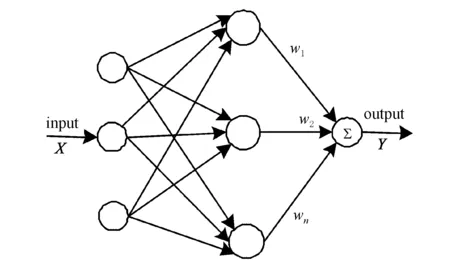
图1 RBF神经网络结构图

(3)

式中：wj为隐含层至输出层的连接权值；j=1，2，…，n，n为隐含层神经网络的个数；bj为隐含层径向基函数的阈值；cj为隐含层第j个基函数的中心；σj为第j个隐含节点的宽度。

一般情况，通过RBF神经网络预测交通流时，其输入层神经元个数与混沌时间序列重构相空间的嵌入维数m相等时，交通流预测具有比较好的效果，因此本文的RBF神经网络预测短时交通流时，其输入层神经元个数取m，即l=m，隐含层神经元数n为经验值2m+1。

由于短时交通流RBF神经网络存在初始权值不能准确获得的缺陷，同时权重wj、径向基参数cj和bj的取值对RBF神经网络的预测精度有很大影响，而PSO是一种基于群体智能的随机全局搜索算法，其基本思想是粒子经过迭代向当前最优粒子靠拢，最后找到最优解，具有全局优化、精度高等优点[10-11]。为了提高短时交通流预测的准确性，利用PSO对RBF的参数进行寻优。

统筹考虑短时交通流的混沌时间序列和非线性特征，采用延迟嵌入定理对短时交通流进行相空间重构，并利用PSO对RBF神经网络的参数进行寻优，进一步设计基于相空间重构和PSO-RBF的短时交通流预测方法，其具体步骤如下所示。

步骤1。初始化参数。确定粒子个数Q、最大迭代次数kmax、加速系数c1和c2，以及惯性权重wmax的和wmin；确定位置和速度取值的范围，对粒子初始位置和初始速度赋予随机值，并初始化个体极值和全局极值；确定RBF神经网络的训练次数等参数。

步骤2。短时交通流时间序列的相空间重构。将短时交通流混沌时间序列处理成归一化时间序列，采用前文提出的方法确定短时交通流时间序列的延迟时间τ和嵌入维数m，将短时交通流时间序列x(i)重构到m维相空间，并计算交通流最大的Lyapunov指数，对交通流的混沌特性进行判定。

步骤3。构建RBF神经网络混沌时间序列预测模型。根据时间序列输入、输出参数个数构建RBF神经网络拓扑结构，将归一化后的训练样本作为输入层，随机生成一个种群粒子Xs=(xs1，xs2，…，xsN)T，Xs为代表RBF神经网络的初始值。

(4)

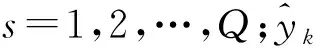
步骤5。根据输入输出样本计算每个粒子位置Wi对应的适应度值，根据初始粒子适应度值确定个体极值和全局极值，并将每个粒子的最好位置作为其历史最佳位置。

步骤6。在每一次迭代过程中，根据式(4)～(5)通过个体极值和全局极值更新粒子自身的速度、位置和惯性权重；在粒子每次更新之后以一定概率pi重新初始化粒子，计算新粒子适应度值，根据新种群粒子适应度值更新粒子个体极值和全局极值。其中pi表达式为

(5)

步骤7。满足最大迭代次数kmax后，将PSO得到的最优粒子对RBF神经网络的连接权值、径向基函数cj和σj参数进行赋值，RBF神经网络预测模型经过训练后，再输入一组短时交通流时间序列进行预测，算法结束。

基于PSR-PSO-RBF的短时交通流预测方法算法流程见图2。

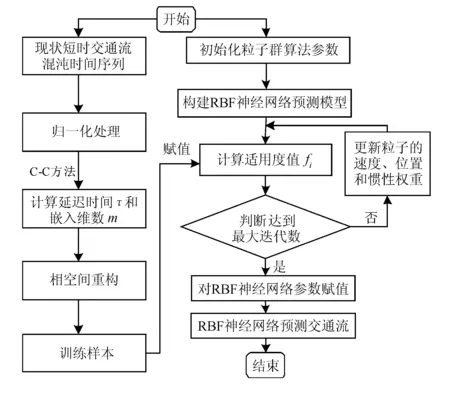
图2 基于PSR-PSO-RBF的短时交通流

3 实例分析

以长沙市某交叉口为实例进行分析。调查该交叉口的一个进口方向的交通流，调查时间为星期四的07:00-12:00，该时间段随机选取，为工作日的一般时间段，每5 min记录1次数据，共记录6周，得到360组数据，即交通流时间序列长度N=360。首先，按式(6)将交通量混沌序列处理成归一化时间序列。

(6)

式中：xi为初始时间序列，yi为归一化的时间序列。然后，基于MATLAB编程，采用前文所提出的方法计算交通流时间序列的嵌入维数m和延迟时间τ，计算结果见图3。

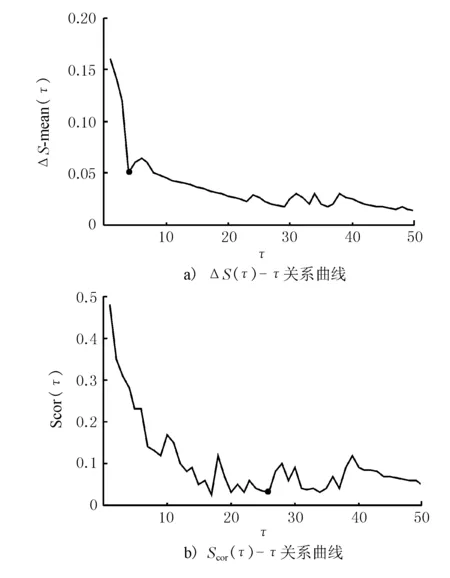
图3 C-C算法计算结果

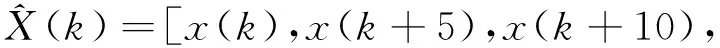
x(k+15),x(k+20),x(k+25)]

式中：k=1，2，…，335。通过小数据量的Lyapunov指数计算方法，得到交通流时间序列最大的Lyapunov指数λ1=0.053 2，说明该交通流时间序列存在混沌特性。

为验证本文预测方法的有效性，将其与基于RBF的短时交通流预测方法(RBF方法)和基于PSO-RBF的短时交通流预测方法(PSO-RBF方法)在相同的条件下进行对比实验：RBF神经网络采用6-13-1的3层结构，训练次数取150，训练目标取0.001，学习率取0.01；粒子群算法的种群规模取40，最大迭代次数为150，加速系数取c1=1.0和c2=1.5，惯性权重wmax=1.0和wmin=0.5，粒子位置和速度取值分别为[-4,4]和[-1,1]。

表1 预测误差结果

图4 {x(300+k)的预测结果

由预测结果可知：①3组实验中PSO-RBF和PSR-PSO-RBF的预测误差均比RBF小，说明PSO优化RBF神经网络能提高RBF预测模型的交通流预测精度；②与PSO-RBF相比，PSR-PSO-RBF的预测误差更小，表明引入的相空间重构技术充分考虑了短时交通流的混沌与非线性特性，短时交通流的预测精度也得到了进一步提升，进一步验证了本文所提预测方法的有效性和先进性；③3组实验中，上述3种方法的交通流预测值与实际交通流的变化趋势总体保持一致，但相比于RBF、PSO-RBF预测方法，文中所提PSR-PSO-RBF预测方法的短时交通流更接近实际交通流量，其预测误差更小，预测结果也更为可靠。

4 结语

高精度短时交通流预测能够为智能交通控制与管理提供强有力的数据支撑，基于PSR-PSO-RBF的短时交通流预测方法不仅可以有效克服传统RBF神经网络的缺陷与不足，还能够进一步提高短时交通流的预测精度。实例结果表明，与基于RBF、PSO-RBF的短时交通流预测方法相比，文中所提出的短时交通流预测方法的误差更小，其预测效果更好，能更好地满足智能交通控制与管理的客观需要。由于短时交通流在一定程度上还会受到短时间内发生突发事件(如临时修路、交通事故等)、节假日和恶劣天气等因素的影响，如何考虑上述因素设计适合于不同情况(如突发事件、节假日大客流)的短时交通流预测方法是笔者下一步要研究的问题。