基于LSTM的疏浚管道流速预测模型

李 雷，倪福生，蒋 爽，姚命宏

（1.河海大学 机电工程学院，常州213022；2.河海大学 疏浚技术教育部工程研究中心，常州213022）

疏浚工程是采用挖泥船以及其它机械设备共同开挖水下土石方工程，广泛用于维护航道、生态环境保护以及吹填造岛等各个领域。通过维护航道，可以控制航道尺寸，提高航运能力；通过对湖泊底泥进行疏浚，可以取走污染物，改善水生态环境；通过吹填造岛，可以扩建岛屿，维护我国领土主权。绞吸挖泥船是疏浚工程中常用的疏浚设备，其工作环节主要分为挖掘和输送两部分，其中输送环节的能耗占整个疏浚系统总能耗的80%以上[1]。绞吸挖泥船的管道输送是以水作为载体，通过封闭管道输送固体物料的运输方式，具有远距离连续输送、效率高、成本低和安全可靠等优点。在管道输送过程中，对泥浆流速的控制至关重要。如果泥浆的流速低于临界流速值，泥沙将在管道阻力较大处产生沉降，会降低挖泥船的产能，甚至会导致泥浆管道堵塞，但如果仅保证泥浆的流速，将泥泵转速设定过高，会增大挖泥船的能耗和加剧管道的磨损[2]。

文献[3]针对大直径浆体输送管道淤积临界流速，提出一种基于反向传播神经网络模型；文献[4]针对浆体管道输送临界流速，提出一种基于极限学习机模型；文献[5]针对极限学习机模型的不足，提出一种基于粒子群优化—极限学习机的流速预测模型。以上模型在一定程度上取得了良好的效果，但疏浚管道输送系统的实际工况十分复杂，泥泵的工作特性、土质、排泥管特性和挖掘深度等都会影响到输送系统的运行状况，因此需要探索出一种适用性强、预测效率高的疏浚管道流速预测模型。

本文提出使用LSTM 对泥浆管道输送系统的流速预测进行建模，并对疏浚管道输送实验台和某真实绞吸挖泥船数据集进行验证，这对流速的控制以及提高管道输送系统的稳定性和安全性有很大帮助。

1 疏浚管道输送系统

1.1 挖泥船管道输送系统工作原理

如图1所示，绞吸挖泥船的管道输送系统主要由吸泥管、泥浆泵、柴油机、机械传动机构、排泥管和各类传感器组成。疏浚作业时，绞刀旋转切削水下泥土，使水下泥土与水充分混合形成泥水混合物。然后泥泵高速旋转使泥泵入口处形成负压，将吸泥管入口处的泥水混合物吸入泥泵。最后泥浆以一定的流速排出泥泵，经排泥管道输送至指定排泥点[6]。

图1 挖泥船管道输送系统的构成Fig.1 Composition of dredger pipeline conveying system

1.2 疏浚管道输送实验台介绍

如图2所示，疏浚管道输送实验台是在参考挖泥船实际管线布置的基础上设计和搭建的，主要由离心泥泵、循环管路装置、电机驱动装置、传感测量系统和监控系统组成。在实验过程中，通过加料斗将泥沙加入输送系统，调整阀门的开度可以改变输送系统的管路特性。上位机可以采集到传感器的实时数据，并对离心泵的转速进行控制。

图2 疏浚管道输送实验台Fig.2 Dredging pipeline transport test bench

1.3 疏浚管道输送系统的输入量

疏浚管道输送系统的工作原理比较简单，但它却是非常复杂的动态特性系统。泥浆的浓度和泥泵的转速与泥浆流速具有很强的相关性。在输送过程中，要保证泥浆流速在临界流速附近，泥浆浓度越高，维持颗粒悬浮所需的能量越高，要求的泥浆输送速度越大。对于泥泵而言，调节泵的转速不仅可以控制泥浆的流速，而且使泵的工作效率保持在最佳状态[7]。

管道输送系统是一个典型的动力系统，可以通过系统的输入量（泥浆浓度、泥泵转速等）和输出量（泥浆流速）之间的函数关系来进行流速的预测。

2 疏浚管道输送系统流速预测模型

2.1 网络构架选择

本文通过尝试不同的构架，并通过仿真选择疏浚管道输送系统合适的网络框架。如图3所示，分别为BP 网络、简单RNN 网络、LSTM 网络的构架。

图3 网络构架对比Fig.3 Network architecture comparison

简单RNN 网络与BP 网络的区别在于：当前隐藏层的输入包含当前输入信号和该隐藏层上一时刻的输出，从而使网络对简单的动力系统具备建模能力。

LSTM 网络与简单RNN 网络的区别在于：LSTM的隐藏层通过增加神经元的复杂性，在前向计算中使用输入门、遗忘门、输出门来保持和控制信息，一定程度上解决了梯度消失以及短时记忆的问题，从而使得网络对复杂的动力系统具备建模能力[8]。LSTM 网络的基本单元如图4所示，其中前向计算过程的公式如下：

图4 LSTM 网络的基本单元Fig.4 Basic unit of LSTM network

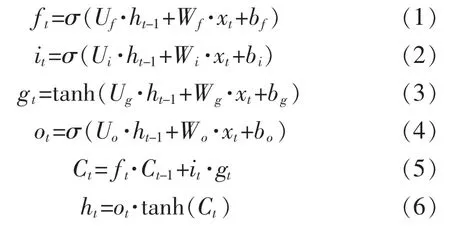
式中：ft，it，ot分别为遗忘门、输入门、输出门；xt，gt，ht，Ct分别为t时刻的输入、输入节点、中间输出和细胞单元的状态；Wf，Uf，Wi，Ui，Wg，Ug，Wo，Uo和bf，bi，bg，bo分别为权重系数和相应门的偏置项；σ，tanh 分别为sigmoid 和tanh 函数变化。

三种构架的第二隐藏层均是为了提高网络的深度，增强网络的预测能力。后面3 层可以视为一个简单的BP 网络，它将网络模型第一隐藏层提取出的特征作为输入，捕捉这些特征和流速之间的函数关系。

本文将训练数据进行离差标准化[9]，对样本数据进行变换使结果值映射到［0，1］，标准化公式为

式中：x，X分别为标准化前、后的数值；xmax，xmin分别为样本数据最大、最小值。

前两种架构较为简单，可以在Matlab 上编写脚本搭建网络并进行仿真。BP 网络的预测结果如图5所示，其平均误差为11.73%，且由于BP 网络无法处理时序数据间的关联信息，使得流速的预测值与真实值之间的误差波动很大；RNN 网络的仿真预测结果如图6所示，其平均误差为9.67%，最大相对误差达到14.04%，误差波动较大。RNN 网络虽然存在记忆功能，但是在误差反向传播时会存在梯度消失和梯度爆炸的问题，无法有效地学习到较早的信息，使得流速的预测值与真实值之间存在着较大的误差。因此BP 和RNN 不适合作为疏浚管道输送系统流速的预测模型，本文对LSTM 神经网络进行探究。

图5 BP 网络预测结果Fig.5 BP network prediction results

图6 RNN 网络预测结果Fig.6 RNN network prediction results

2.2 网络控制量选择

模型需要根据实际工况选择控制量，当网络模型的预测精度难以达到要求时，需要额外的信号来辅助模型建模。产生这种现象的原因可能有很多，比如：

（1）已有信号的选取不准确或不完整；

（2）实际的动力系统的状态方程中存在随机变量；

（3）传感器测得的信号中混入了噪声。

为了检验LSTM 网络的普适性，本文对疏浚管道输送实验台和某真实绞吸挖泥船的数据集进行验证。两个对象的网络控制量如表1所示，对于疏浚管道输送实验台，将泥泵转速（n）、泥泵扬程（H）、泥浆浓度（Cv）作为输入到LSTM 网络的控制量。对于绞吸挖泥船，由于施工现场采集的数据噪声污染以及延时较为严重，仅依靠泥浆浓度、泥泵转速、泥泵扬程等信号难以达到预测效果，因此另外添加历史流速（vt-1）作为辅助。

表1 预测对象的控制量Tab.1 Amount of control that predicts object

2.3 网络训练

在模型的搭建过程中，搜索LSTM 网络参数的难点在于它的准确性和快速性。一方面，如果在有限时间内搜索到的参数未捕捉到控制量与输出量之间的关系，那么基于这组参数的LSTM 网络的流速预测值就不可能精准；另一方面，如果需要很长的时间才能搜索到合适的网络参数，那么该模型不能实时预测泥浆流速，这个训练算法以及整个流速预测模型将失去使用价值。在多次尝试后，本文最终采用批梯度下降算法（minibatch stochastic gradient descendent algorithm），结合Adam 梯度计算技术有效地解决这个问题[10]。网络训练的流程如图7所示，流程步骤如下：

图7 网络训练流程Fig.7 Flow chart of network training

步骤1抽取训练样本，使用样本前半部分数据进行网络训练，后半部分数据留作模型预测检验；

步骤2在当前训练样本中，逐一计算各个时间点上网络模型预测的泥浆流速值，并存储中间计算过程；

步骤3累加泥浆流速预测值与真实值之间的误差；

步骤4将步骤3 中计算得到的误差，采用Adam梯度计算方法计算各个网络参数的梯度，并更新网络参数；

步骤5判断当前训练样本中的所有时间节点是否完成。如果没有完成，则转步骤2，如果完成则转步骤6；

步骤6判断是否达到最大样本训练个数，如果没有达到最大训练样本数目，则转步骤1，如果已经达到则算法结束，保存网络参数。

3 预测结果分析

3.1 实验台预测结果

如图8所示，在将泥浆流速归一化后，模型预测的泥浆流速值与真实值之间平均误差为1.42%。由于实验台采集的数据噪声污染不严重，仅依靠泥泵转速、泥泵进出口压力、泥浆浓度这4 个参数就能够准确预测出泥浆流速。其中有两个现象需要指出：

图8 实验台数据预测结果Fig.8 Experimental data prediction results

（1）整个实验数据总共有18000 样本点，因为训练时在前10000 个样本中随机抽取了训练样本，所以网络模型在前半部分数据上的预测效果要好于后半部分数据上的表现。

（2）在接近13000 s 时，传感器意外产生一个噪声点，泥浆流速突然变为零后立刻恢复正常。但网络模型在该时间预测的泥浆流速依然保持正常，可见该流速预测模型已经成功捕捉该疏浚管道输送系统中控制量与输出值之间的关系。

3.2 绞吸式挖泥船预测结果

如图9所示，未将历史流速作为输入时，模型在速度变化较快的情况下无法达到预测效果，该网络模型未能完全捕捉到高流速时控制量与输出值之间的关系；如图10所示，将历史流速作为输入后，绞吸挖泥船的预测值与真实值的平均误差控制在1.31%以内，该网络模型已经捕捉到控制量与输出值之间的关系，可以精准预测泥浆流速。

图9 未采用历史流速作为输入的预测结果Fig.9 Historical flow rate was not used as input for prediction

图10 采用历史流速作为输入的预测结果Fig.10 Historical velocity was used as input for prediction

4 结语

本文提出了一种基于LSTM 循环神经网络的疏浚管道流速预测模型，并对网络构架的选择、网络控制量的选择和网络训练进行了详细的阐述。实验表明LSTM 对疏浚管道流速的预测具有较强的普适性和准确性，在实验台的数据集和挖泥船的数据集上均能精准预测疏浚管道流速。该模型为管道输送系统的流速预测提供了新思路，同时对疏浚管道流速的预测控制具有一定的指导意义。