基于受限玻尔兹曼机的神经元群体响应的贝叶斯解码

杨 晨，刘心声

（南京航空航天大学 理学院，江苏 南京 210016）

研究神经元群体如何表达和传递信息是神经科学的一个重要方向，对于我们理解视觉系统的功能具有重要意义。近20年来的研究表明，神经回路中细胞的活动具有强烈的相关性[1-3]，这些相关性很大一部分是由刺激引起的，群体中的不同神经元可能对刺激的共同特征做出响应，并通过这种共同的响应相互关联。另一方面，大脑区域的神经元之间具有“噪声相关性”，即在给定刺激下神经元输出嘈杂的响应之间仍然存在相关性。研究表明，在含有多个神经元的群体中考虑噪声相关性有利于描述感觉神经元对刺激的反应[4]。

分析两图得到皖河泥沙特征：第一，径流量与含沙量波动呈正相关，月峰值同时出现；第二，上游支流潜水含沙量大于干流皖河；第三，1995年后，石牌站和潜山站年平均含沙量波动区间显著下降。

基于此，本文考虑神经元群体对刺激的共同特征产生的响应之间可能存在相关联的情况，利用机器学习中的受限玻尔兹曼机模型模拟神经元群体的编码过程，并构建解码器用于模拟小鼠视觉皮层神经元由光栅方向引起的响应序列中，实现对光栅方向的解码。

1 最大熵模型

已有研究大都采用二进制框架来描述神经元群体的动作电位：对于包含n个神经元的群体，σi表示第i个神经元在很短时间区间内的响应，当σi为0时表示第i个神经元在时间段内没有产生动作电位，当σi为1时表示第i个神经元在时间段内至少产生一个动作电位。在这个框架下，整个神经元群体可能的响应模式有2n种，需要建立合适的概率模型来描述在给定刺激s下每种响应模式的概率。

统计物理中的最大熵（ME）模型[5]是描述神经元群体响应的一种常用模型。最大熵模型的思想是首先选定一些描述性的统计数据，计算它们在样本中的值，在所有可以重现这些统计数据的模型中寻找熵最大的分布。最大熵模型的形式为

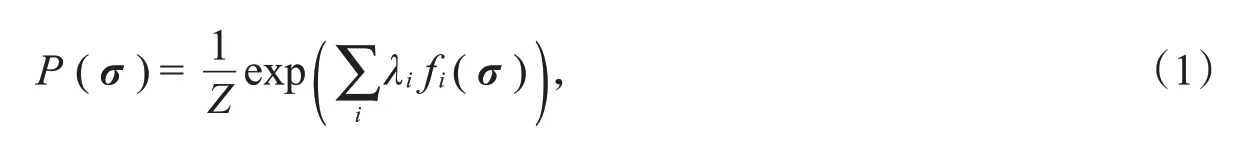
其中，σ是神经元群体的响应向量；f i(σ)是选取的统计值，它是σ的任意函数；Z是配分函数，它很难通过计算得到，但是在大部分模型中并不需要计算出Z的实际值；λi是拉格朗日乘子。

采用SPSS 21.0软件进行统计分析，计量资料用均数±标准差表示，满足正态性，用t检验，不满足正态性，用秩和检验。计数资料用x2检验。

有些教师为了赶进度，将更多时间花在强调单一概念上，学生则是很盲目地接收信息，出现了学生不明确课程目标，缺少能动性的现象。在课堂中，部分教师由于课时紧张，往往选择删减案例，仅保留关键语句的讲解和圈画。但是，关键定义的陈述往往需要论据加以论证才能在学生心里留下深刻印象。这种做法也导致不能有效拓展第二课堂，缺少具体的教学辅助资料，课程内容受限，教学资源急剧减少。有限的教学时间导致很多教师只能依靠考试和作业这两种单一形式来检验学生的阶段性和长期性学习成果，缺少多样化的评价方式。

最大熵模型的实际形式与约束条件有关，最简单的一种最大熵模型是独立模型。在该模型中f i(σ)=σi，即对每个神经元的平均放电活动做约束，使得

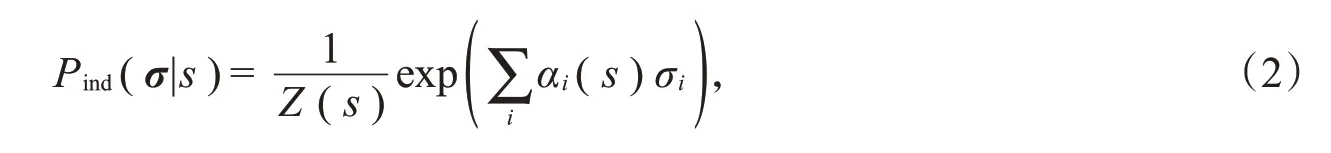
其中，Z(s)是配分函数，αi(s)是控制第i个神经元响应的参数，s是离散的刺激集{s1,s2,s3,…,s q}中的任一刺激。这种模型简单、便于计算，但忽略了神经元响应之间的相关性。

为了描述神经元之间的两两相关性，Schaub等[6]在独立模型的基础上增加了模型中神经元之间的成对相关性与数据中神经元之间的成对相关性相等的约束条件，即

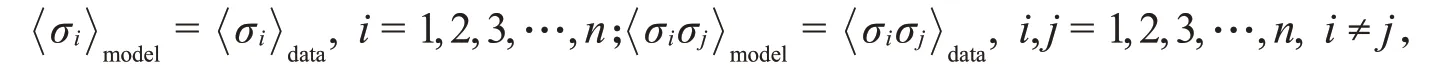
总之，在大风降温前应做好防风保温准备，为猪只创造良好的生存环境，以维持猪群的稳定，充分发挥猪只的生产性能，提高猪场的效益。

为了降低油泥的处理费用，减少固体废物产生量，抚顺矿业集团根据油泥中含有大量油的特点，开发并建设了油泥过滤与复用装置，通过物理方法回收其所含的大部分油、水后，将泥饼与油页岩尾矿混合压锭，再作为原料送回干馏炉。油泥过滤与复用装置的工艺流程见图5。

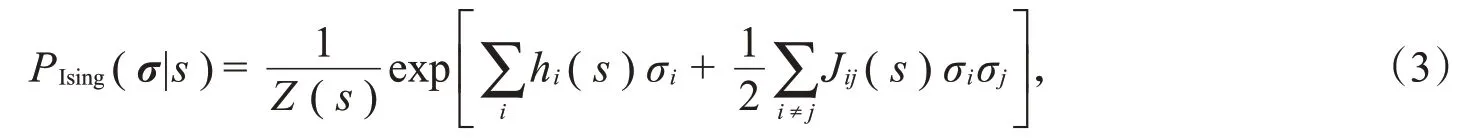
其中，h(s)=(h i(s))和J(s)=(J ij(s))分别是控制单个神经元的活动和成对神经元的交互作用的参数。Ising模型也被称作二阶最大熵模型，因为与独立模型相比，它可以准确描述神经元之间的两两相关性，但在描述更高阶的相关性方面效果不佳。在Ising模型的基础上，继续增加三阶相关性和更高阶相关性的约束：

α(s)和β(s)分别是控制响应单元和隐藏单元活动的参数，在统计物理中被称为外场，W(s)是响应单元与隐藏单元之间的连接权重矩阵，在统计物理中被称作耦合，通过这些与刺激相关的参数描述由刺激引起的相关性。对于离散的刺激集，需要估计的参数随着刺激的数量呈线性增长。假设有n个神经元、m个隐藏单元和q个刺激，则模型有(n+m+n×m)×q个参数。

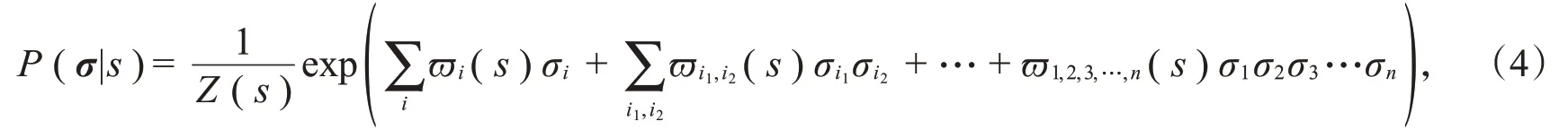
参数ϖi1,i2,i3,…,i q用来描述神经元i1,i2,i3,…,i q之间交互作用大小，若ϖi1,i2,i3,…,i q=0，则表示神经元i1,i2,i3,…,i q之间不存在交互作用，Z(s)是配分函数。这种模型在理论上可以描述神经元之间任意阶的相关性，但是描述越准确，需要的模型参数越多，因此在实际中难以学习。

1.3.3 血浆ET‐1测定 检测试剂盒来自深圳晶美物工程有限公司，在治疗前后抽取空腹静脉血3～5 mL，抗凝后4℃下3 000 r/min离心10 min（离心半径15 cm），分离上层血清，采用ELISA法检测血清ET‐1的含量。

2 神经元群体响应编码与解码模型

2.1 基于受限玻尔兹曼机的编码模型

或写作矩阵形式：

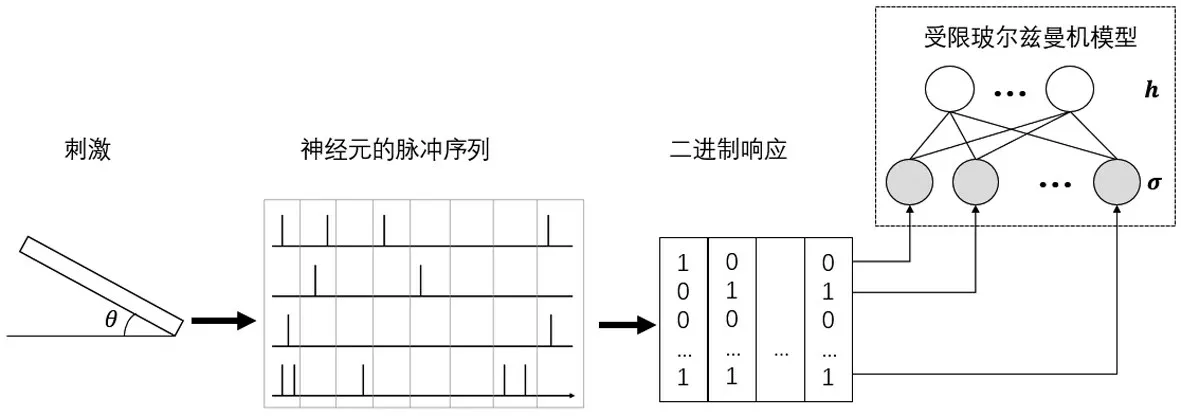
图1 基于受限玻尔兹曼机的神经节细胞编码模型

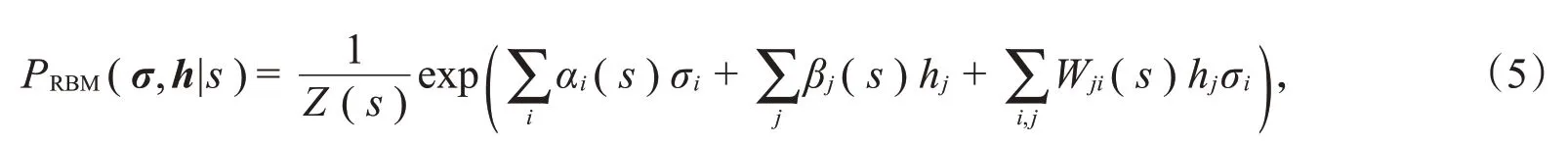
由上述模型可知，很难直接对神经元之间的高阶相关性建模。因此，本节引入机器学习中的受限玻尔兹曼机（RBM）模型[8]，利用模型中隐藏层的隐藏单元来模拟神经元之间的复杂交互。将神经元响应的相关性分为由刺激引起的相关性和噪声相关性，其中刺激相关性是指群体中不同神经元对刺激的共同特征做出响应产生的相关性，噪声相关性是在给定刺激后，重复多次实验得到的神经元嘈杂反应之间的相关性。如图1所示，利用受限玻尔兹曼机模型描述每个刺激s下神经元群体响应模式的概率P(σ|s)，受限玻尔兹曼机是一种具有可见层和隐藏层两层结构的随机神经网络模型，它们的联合概率可以写作：

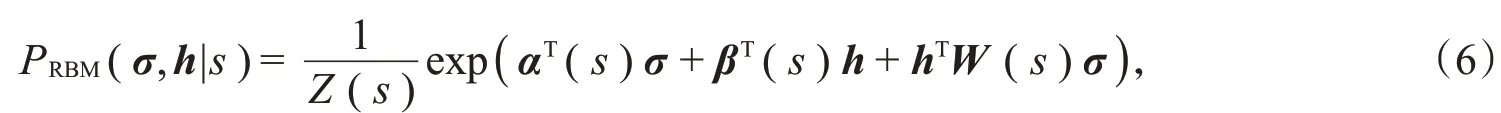
其中，σ=(σ1,σ2,σ3,…,σn)是可见层单元，用来描述可观察到的神经元群体响应；h=(h1,h2,h3,…,h m)是隐藏单元，σi∈{0,1}，h j∈{0,1}，i=1,2,3,…,n；h=1,2,3,…,m。受限玻尔兹曼机的隐藏层单元h不对应于实体，只是用来简化模型的一些抽象变量以捕获神经元之间的噪声相关性。每一个隐藏层变量都与多个神经元交互，与同一个隐藏变量交互的神经元通过这个隐藏变量建立联系，隐藏变量的存在大大简化了模型。Z(s)是配分函数，形式为

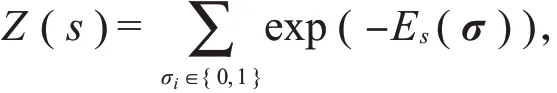
RBM模型中神经元的边缘分布为

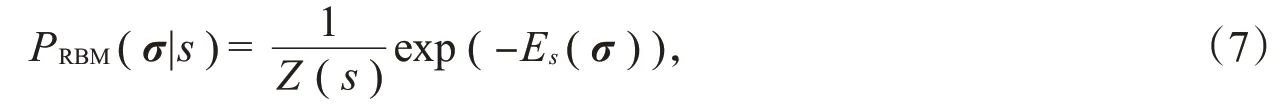
这时，我们走到蕉园附近，高大的父亲从蕉园穿出来，全身也湿透了，“咻！这阵雨真够大！”然后他把我抱起来，摸摸我的光头，说：“有给雷公惊到否？”我摇摇头，父亲高兴地笑了：“哈……金刚头，不惊风，不惊雨，不惊日头。”

式（7）即为RBM编码模型的最终形式。下面给出式（7）的证明。

Hinton提出了k步对比散度算法[9]学习RBM参数，其大致思路是：将训练集中的任意一个样本σ作为初始化可见变量σ(0)，进行k次Gibbs采样，如图2所示，得到σ(k)，并在每次采样中执行梯度上升算法：

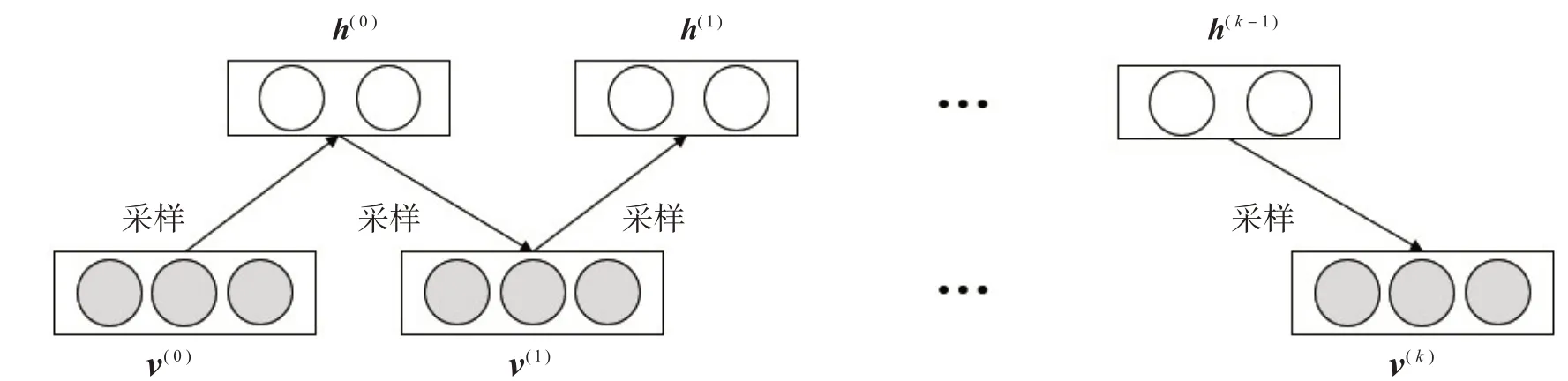
图2 Gibbs采样过程

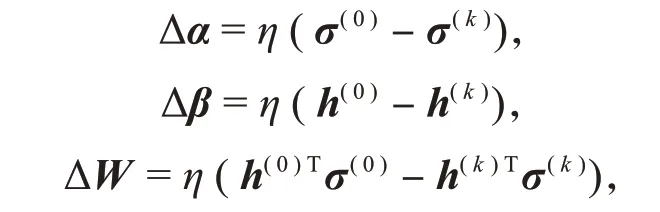
其中，η是学习率。更新参数θ={W,α,β}的值，得到训练后的RBM模型。

2.2 基于贝叶斯定理的解码模型

在建立编码模型后，希望模拟大脑在接收到视网膜通过动作电位传递的视觉信息，如光条的倾斜角度变化后，分析看到的光条倾斜角度是70°、75°、80°，还是85°的过程。为此，建立解码模型，从观察到的神经元放电序列σobs中解码它是由哪一个刺激引起的。

下面模拟小鼠视觉皮层神经元由刺激引起的群体活动响应模式，其中刺激是每次在黑暗的背景上出现的一个白色光条，它有q种可能的倾斜角度，分别为i·180/q，i∈{1,2,3,…,q}，对应于解码过程中刺激的取值范围。例如，q=6时，光条的倾斜角度分别为30°、60°、90°、120°、150°和180°，将每个刺激重复10 000次，模拟每个刺激下小鼠视觉皮层神经元的10 000组放电序列。将这些数据分为训练集和测试集，训练集用来学习受限玻尔兹曼机模型的参数，得到编码模型；测试集用来评估解码模型的准确性，利用解码器对测试集中的响应序列解码，判断它是由上述6个刺激中的哪一个引起的。

其中，P(s|σobs)是刺激的后验分布，根据贝叶斯定理，它可以写做

综合正交实验的结果，以CODCr和UV254为主要分析指标，采用单因素变量法[9]，分别考察废水pH值、石墨烯加入量以及H2O2加入量对废水CODCr去除率和出水UV254值的影响。

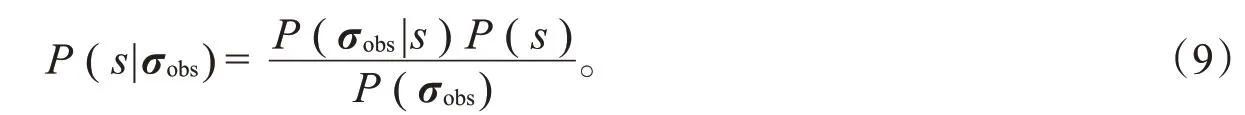
P(σobs)与刺激s无关，因此它与式（8）中的最大化表达式无关，最终的解码模型表达式为

由于咨询单位与设计单位往来的文档均为电子版，公司工作成果信息载体主要是OFFICE文档、PDF格式文件、WPS文档，接收的文档类型有DWG、DWF、PDF格式文件，OFFICE文档，WPS文档，适合于开展信息化建设。

3 模拟神经元群体的放电序列

利用最大后验进行解码：

在模拟小鼠视神经节细胞群体的响应时，假设群体中神经元的偏好方向在0°～180°范围内均匀分布。因为每个神经元的调谐曲线是钟形的，所以这里采用Von Mises分布来拟合神经元的调谐曲线，它是一种圆上的连续概率分布模型，形式为

徐进步被他瞪得一哆嗦,赶紧摆手道:“不是我说的,是他!我从不背后说领导的怪话。”他又企图往赵天亮身上赖,赖人仿佛也有惯性。

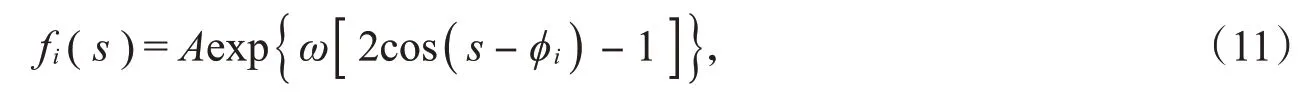
其中，φi是第i个神经元的偏好方向，A是第i个神经元在偏好方向上的放电率，ω是控制调谐曲线的刻度参数。ω越大，调谐函数曲线越尖峭，越向φi的邻近集中；ω越小，调谐函数曲线越平缓；当ω趋于0时，Von Mises分布趋于均匀。这些参数由文献[10]中的实验数据得到。

分别模拟同质神经元群体和异质神经元群体的调谐函数。对于同质神经元群体，每个神经元的最大放电率和调谐曲线的宽度相同，只有偏好方向不同。图3（a）给出了同质群体中6个神经元的Von Mis‐es调谐函数图像。对于异质神经元群体，每个神经元的最大放电率和调谐曲线宽度不同，如图3（b）、（c）、（d）所示。

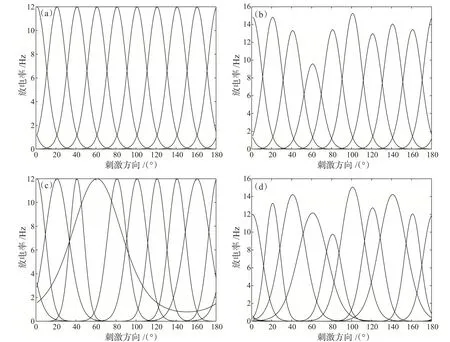
图3 包含6个神经元群体的调谐函数。（a）同质神经元群体；（b）最大放电率异质神经元群体；（c）调谐宽度异质神经元群体；（d）最大放电率和调谐宽度异质神经元群体

最后，利用Jakob[11]文中的二分高斯分布生成神经元群体的二进制响应序列。

4 实验结果

根据上述方法模拟了每个刺激下10 000组小鼠视觉皮层神经元放电序列，其中，9 000组作为训练集，用于学习模型的参数，另外1 000组作为测试集，用于测试解码器的性能。利用解码的正确率来评估解码器的性能，它的定义为

图4（a）展示了不同数量的刺激下基于RBM模型与独立模型解码器的解码正确率，其中，神经元群体是同质的，神经元的个数为50，受限玻尔兹曼机中隐藏单元的个数为30。从图中可知，随着刺激数量的增加，两解码器的正确率都会降低，这是由于增加刺激数量后，不同刺激之间的差异变小，从而使得解码的问题更加复杂。另一方面，对于不同数量的刺激，基于RBM模型的解码器都有更好的性能，这表明考虑由刺激引起的神经元之间的相关性可以提高解码精度。图4（b）展示了固定刺激个数为4，受限玻尔兹曼机中隐藏单元个数为30时，基于RBM模型与独立模型的解码器的解码正确率。结果表明，当刺激数量固定时，随着群体中神经元数量的增加，两种解码器的性能都会提高，且基于RBM模型的解码器始终具有更高的正确率。

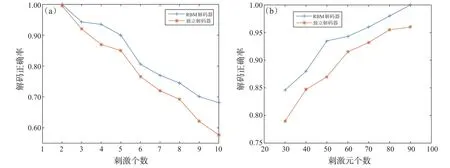
图4 RBM解码器与独立解码器的解码性能。（a）两种模型的解码正确率与刺激个数的关系；（b）两种模型的解码正确率与群体中神经元个数的关系

现研究RBM解码器的性能与模型中隐藏单元个数的关系，及两种解码器对异质神经元群体的解码性能，结果分别如图5和6所示。

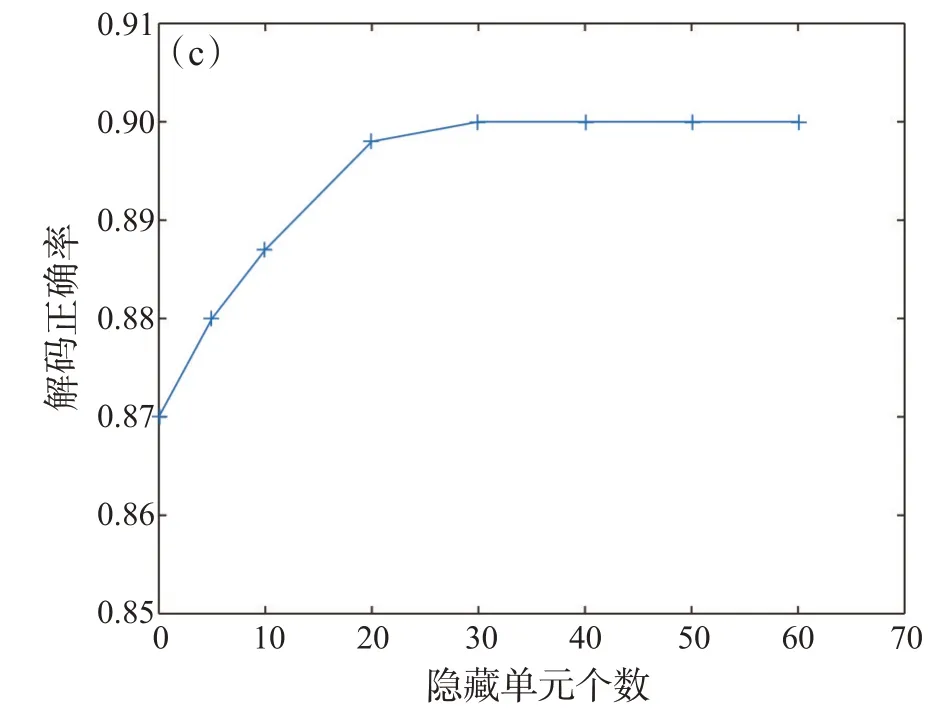
图5 包含不同数量隐藏单元的RBM解码器的正确率

图5显示了包含不同数量隐藏单元的RBM解码器的准确率。结果表明，当隐藏单元的个数达到20时，解码器的性能趋于饱和。图6给出了不同数量的刺激下RBM模型和独立模型对同质神经元群体和异质神经元群体的解码精度，可见，对于异质神经元群体，RBM解码器和独立解码器的准确率都有提升，这可能是由于群体中神经元具有一定的变异性，从而使得不同刺激的响应数据特征更加具体。

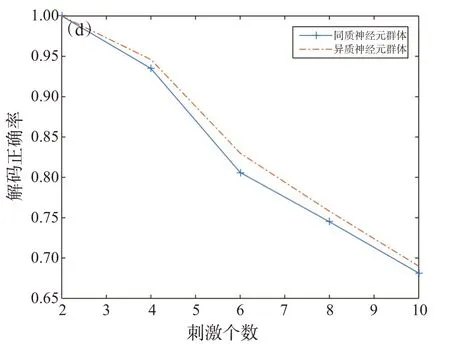
图6 受限玻尔兹曼机解码器的解码精度（神经元个数为50）

5 结束语

综上所述，利用受限玻尔兹曼机模型可以从模拟的大规模神经元群体活动中解码离散的方向刺激。与传统的独立解码器相比，受限玻尔兹曼机模型的解码器考虑了神经元群体响应的相关性结构对刺激的依赖性，因此解码性能更好。数值模拟结果表明，对于两种模型，解码性能随着群体中神经元个数的增加而增强，随着刺激数量的增加而减小。对于异质的神经元群体，两种解码器的解码性能都有提高。本文所提出的解码器对于模拟神经元响应的解码效果更好，在今后的工作中，我们会进一步将其应用于实验数据进而评估它的性能。