基于高光谱数据的土壤全氮含量估测模型对比研究

殷彩云，白子金，罗德芳，彭 杰

（塔里木大学植物科学学院，新疆 阿拉尔 843300）

土壤全氮是衡量土壤肥力水平的重要指标之一，土壤氮含量指标被广泛用于土壤养分供应能力、植物养分吸收和利用规律等农化分析中［1］，如何快速、准确和高效地监测土壤全氮含量，对作物生长和科学合理施用氮肥有重要意义。传统测定土壤全氮含量的方法，不仅有耗时、耗力、成本高、环境污染等缺点［2-4］，而且在测定过程中一些化学试剂容易对人体造成危害，这种方法显然不能满足生产中大面积快速监测土壤全氮含量的需求。近年来，高光谱技术被广泛用于土壤化学组分的测定，而基于光谱学原理的土壤氮素含量测定方法具有及时、省力、简便、无污染等优点［5］，可为快速监测土壤全氮含量提供一个有效途径。

随着科学技术的进步，高光谱技术的发展为高效快速监测土壤养分提供了新的技术和方法。目前，国内外学者利用高光谱技术分析土壤全氮的相关研究已取得较大进展。Hummel等［6］研究发现土壤全氮含量与光谱反射率在可见光和近红外波段相关性很高。Reeves等［7］利用近红外光谱反射率特征波段建立的模型可对土壤全氮含量进行有效估测。Chang等［8］利用偏最小二乘法（PLSR）建立的基于光谱分析的模型可有效估测土壤全氮含量。前人的研究结果表明，利用土壤光谱反射率数据可进行土壤全氮含量估测，为后续的研究打下坚实基础。卢艳丽等［9］利用可见光550和450 nm组成的光谱指数构建了土壤全氮含量预测模型，预测集R2达到了0.82以上。彭杰等［10］以895、1079、1138 nm等8个敏感波段反射率对数倒数的一阶微分建立的多元逐步回归模型R2达到了0.83。李焱等［11］通过提取特征波段，以多元逐步线性回归和偏最小二乘回归建模，发现反射率经二阶微分变换后，以偏最小二乘回归建模R2达到了0.96。王一丁等［12］对光谱反射率进行倒数对数和正交信号校正变换后，以PLSR建立的土壤全氮估测模型R2为0.92。近年来，国内一些研究多以高光谱数据结合非线性建模方法建立土壤养分含量估测模型，由于土壤光谱反射率和土壤养分含量之间是一种非线性关系，因此用非线性模型来估测土壤养分含量效果更好。如王世东等［13］、高小红等［14］、张娟娟等［15］利用PLSR和BPNN两种建模方法与光谱反射率及其数学变换建立土壤全氮估测模型，均具有较好的预测能力。郑立华等［16］提取贡献率超过99.98%的主成分建立BP神经网络全氮含量模型，预测R2达到了0.81。以上研究表明，基于高光谱数据建立的模型是可以对土壤全氮含量进行估测的，但由于土壤类型和地区性差异，在实际工作中很难找到一种通用的模型来估测土壤全氮含量。

随机森林（RF）是一种较新的数据挖掘模型［17］，具有运算速度快、稳定性高、数据适应能力强、在处理大数据集时预测精度高且不易产生过拟合等优势［18-19］。马利芳等［20］利用RF法构建了土壤盐分主要离子估测模型。张智韬等［21］基于微分变换构建的SVMDA-RF模型预测了土壤有机质含量。目前RF多用于土壤有机质和土壤重金属等估测，而用于土壤全氮含量的估测研究较少。因此，本研究利用新疆南疆5县土壤样品的高光谱和全氮含量数据，运用偏最小二乘回归（PLSR）、支持向量机回归（SVM）和随机森林回归（RF）3种方法，结合光谱反射率（R）及一阶微分（FD）、倒数（1/R）、对数（lgR）和连续统去除（CR）变换数据分别建立研究区全区和分区土壤全氮含量估测模型。通过分析比较不同建模方法和不同数据变换后的估测模型精度，挑选出最优全氮含量估测模型，为研究区大范围快速准确获取土壤全氮含量提供技术支撑。

1 材料与方法

1.1 研究区概况

阿克苏地区位于新疆维吾尔自治区中部，天山山脉南麓，塔里木盆地北部，其地理坐标为78°03′～84°07′E、39°30′～42°41′N，属于暖温带大陆性气候，年降水量42.4～94.4 mm，但年蒸发量高达1200～1500 mm［22］，年均气温9.9～11.5℃，光热资源丰富，昼夜温差大［23］。和田地区位于新疆维吾尔自治区最南端，南连昆仑山，东部与巴音郭楞蒙古自治州毗邻，北部与阿克苏地区相邻，西部连喀什地区，地理位置为77°31′～84°55′E、34°22′～39°38′N，年均降水量35 mm，年均蒸发量2480 mm，属于暖温带极端干旱荒漠气候［22］。本研究选取的温宿县、拜城县、和田县、新和县和阿瓦提县隶属于阿克苏及和田地区。研究区种植作物以棉花、水稻、红枣、苹果、香梨、核桃为主，土壤类型主要以壤土和砂壤土为主，其保肥保水能力较差，土壤氮素含量普遍偏低，且该地区盐渍化程度较高，严重影响作物的正常生长发育，对农业经济收入造成了一定的制约。

1.2 土样采集与处理

本研究土壤样品采集地点（图1）和采集数量分别为温宿县105个、拜城县78个、阿瓦提县60个、新和县47个以及和田县107个，共采集397个土壤样品。为保证土壤样品采集的精准性，用网格布点法采集土样，各采样点间距约为100 m，采样深度为0～20 cm，每个土样采集重量为500 g左右。土样带回室内后，去除杂草、砾石及动植物残骸等杂质，在室内自然风干。风干后的土样经研磨混匀后分成两份，一份过2 mm筛，用于光谱数据的测定，一份过0.25 mm筛，用于土壤全氮含量的测定。

图1 样区分布图

1.3 样品分析

采用半微量开氏法测定土壤全氮含量，每个土样设3次重复，重复间相对误差控制在5%以内，取3次测量结果的平均值为最终测定值。各地区土壤全氮含量描述性统计见表1，由表1可知，全氮含量最大值出现在温宿县，为1.89 g/kg，最小值出现在新和县，仅为0.07 g/kg，总体平均值为0.62 g/kg，各地区变异系数为10%～60%，根据雷志栋等［24］对变异系数的等级划分，该研究区的土壤全氮含量属于中等变异，有利于模型的构建。

表1 各地区土壤全氮含量描述性统计

1.4 光谱数据的测定

采用美国ASD公司的FieldSpec Pro FR型光谱仪进行土样光谱数据的测定，其测定波长范围为350～2500 nm，光谱分辨率在350～1000 nm为3 nm，在1000～2500 nm为10 nm，数据重采样间隔为1 nm［25］。测定土样光谱前利用标准白板和黑板对光谱仪进行校准和调整。采集光谱时，为了减少外界环境对测定结果的影响，将土样放置于直径10 cm、深1.5 cm的内部涂黑的培养皿中，以50 W卤素灯为测定光源，距离土样表面70 cm，天顶角为30°，传感器探头位于土样表面垂直上方15 cm处，采用25°视场角探头，每测定一个土样光谱进行白板校正，每个土样采集10条光谱曲线，算数平均后得到该土样的实际反射率光谱数据［26］。

1.5 光谱数据预处理

由于光谱曲线的350～399和2401～2500 nm波段受外界噪声影响较大，故将其去除［13］，仅选取400～2400 nm波段进行光谱分析。为消除样品间散射导致的基线偏移和减少平滑对有用信息的影响，本文采用了多元散射校正（multiplicative scatter correction，MSC）和Savitzky-Golay7点平滑对原始光谱反射率数据进行预处理，得到的反射率（R），并结合一阶微分（first derivative，FD）、连续统去除（continuum removal，CR）、倒数（1/R）和对数（lgR）对反射率（R）进行数学变换。

1.6 建模方法及模型评价指标

建模思路为分区建模和全区建模，以所有采样点获得的数据进行全区建模，以各县采集的数据（共5个县）进行分区建模。为保证模型建立和验证的合理性，所有模型的建模集和预测集都以全氮含量由低到高进行排序进行等间距抽样，以2∶1划分成建模集与预测集。建模方法选用偏最小二乘回归（partial least squares regression，PLSR）、支持向量机回归（support vector machines，SVM）和随机森林回归（random forest，RF）3种方法。PLSR和SVM建模和验证在The Unscrambler X 10.5中完成，RF建模和验证在R语言中完成。

模型评价指标选用决定系数（determination coefficient，R2）、均 方 根 误 差（root mean square error，RMSE）和相对分析误差（relative percent deviation，RPD）。其中，R2表示预测值与实测值之间的拟合程度，R2越大，说明预测值与真实值越接近，模型精度越好；RMSE表示预测值偏离真实值的程度，对于同一组数据，RMSE越小，说明预测值越接近真实值；RPD表示模型预测能力的强弱，根据Chang等［4］对RPD的等级划分，当预测模型的RPD≥2时，表示该模型有较好的估测能力；当1.4≤RPD＜2.0时，表示该模型可以对样品含量进行粗略估测；当RPD＜1.4时，表示该模型预测能力很差，无法对样品含量进行估测。

2 结果与分析

2.1 不同全氮含量土壤反射率光谱特征

根据土样将全氮含量分为4个等级，分别为等级1（＜0.5 g/kg）、等级2（0.5≤TN＜1.0 g/kg）、等级3（1.0≤TN＜1.5 g/kg）和 等 级4（≥1.5 g/kg）。图2为根据每个等级的平均反射率得到4条反射率光谱曲线，由图2可知，不同全氮含量土样光谱曲线的变化规律基本一致，反射率变化范围为0.15～0.50，在全波段范围内，土壤全氮的光谱曲线变化整体呈缓慢上升趋势，在1415、1920、2220 nm波段处有明显的吸收特征。在可见光400～780 nm波段，光谱曲线较陡峭，反射率增长速度较快；在780～1900 nm波段，光谱曲线较平缓，反射率增长速度较慢；在1900～2100 nm波段，土壤光谱反射率随波长的增加而增大，在2100 nm左右波段，反射率值达到最大值；在580～2400 nm波段土壤反射率也是随着土壤全氮含量的增加而增大，但在400～580 nm波段并未呈现这样的规律，出现了交叉现象。

图2 不同全氮含量土壤光谱反射率

2.2 土壤全氮含量与高光谱数据的相关性分析

将土壤R经FD、CR、1/R和lgR变换后，分别与土壤全氮含量做相关性分析，相关系数曲线如图3。由图3可知，土壤全氮含量与R在部分波段达到了较好的相关性；数据经FD变换后，在近红外波段达到显著性水平的波段数明显减少，但有极少波段相关性有所提高，而大部分波段相对于R的相关性并未得到改善，反而有所下降；数据经CR变换后，在全波段内，土壤全氮含量和反射率数据相关性达到显著性的波段数有明显增加，且大多数波段相关性达到了极显著水平，最大相关系数达到了0.43，是一种较好的光谱变换形式；数据经1/R和lgR变换后，lgR变换后的相关性曲线和反射率R相关系数曲线走势基本相同，差异较小，1/R变换后的相关系数曲线与R相关系数曲线相对称，三者达到显著性水平以上的波段数基本相同。

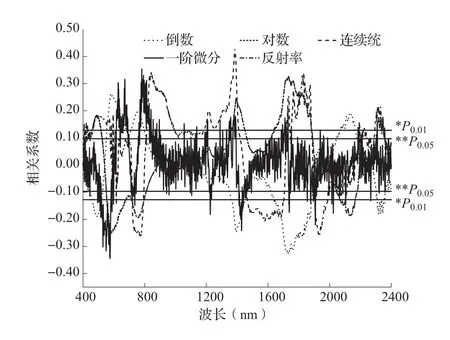
图3 全氮含量与高光谱数据的相关分析

2.3 土壤全氮含量估测模型的建立与检验

为了得到土壤全氮含量最优估测模型，本文针对性地使用反射率及其4种数学变换后数据，利用PLSR、SVM和RF对5个地区土壤全氮含量进行建模，各模型结果见表2。由表2可知，3种方法建立的模型效果各不相同，在进行分区建模时，PLSR最优模型建模集的R2为0.83，RMSE为0.14 g/kg，预测集R2为0.73，RMSE为0.17 g/kg，RPD为1.82，未达到2.0以上，说明PLSR模型效果一般，只能对样品全氮含量进行粗略估测；SVM最优模型建模集R2为0.78，RMSE为0.16 g/kg，预测集R2为0.75，RMSE为0.16 g/kg，RPD为1.97，也未达到2.0以上，说明SVM模型也只能对样品全氮含量进行粗略估测。SVM较PLSR模型，建模集的R2虽然下降了0.05，但预测集的R2上升了0.02，RMSE下降了0.01 g/kg，RPD上升了0.15，说明SVM模型的预测能力略高于PLSR模型。而RF最优模型建模集的R2为0.87，RMSE为0.08 g/kg，预测 集R2为0.86，RMSE为0.08 g/kg，RPD达 到 了3.52，说明RF模型预测能力较好，可以对样品全氮含量进行精确估测。

全区模型与分区模型相比，PLSR、SVM和RF进行全区建模时，建立的最优模型RPD分别为1.50、1.62和3.24，均低于分区最优模型，但PLSR和SVM模型的RPD均大于1.40，可以对样本全氮含量进行粗略估测；而分区建模部分地区建立的PLSR和SVM模型不能用于全氮含量估测，说明全区模型的稳定性要高于分区模型。3种模型相比较，RF模型建模集R2为0.80～0.87，预测集R2为0.76～0.85，RPD为2.35～3.52，RF估测全氮含量的结果较稳定，整体估测精度较高，是一种较好的建模模型。

由表2分析可知，不同数据变换后，模型的精度也有所变化，在5个不同地区，由于土壤类型和采样数量的不同，各种数据变换后建模精度无明显变化规律。PLSR、SVM和RF最优模型分别是在光谱R数据经CR、1/R和lgR变换后建立的。在5个地区建立的最优模型均是RF模型，在和田县、阿瓦提县和新和县，数据经lgR变换后，建立的模型精度最高，而在拜城县和温宿县，数据分别经1/R和CR变换后，建立的模型精度最高。其中阿瓦提县和新和县以PLSR和SVM建立的模型精度明显低于其他地区，可能是由于这两地区采样点位置比较集中，采样数较少，土壤类型单一，总体缺乏代表性，构建的模型效果较差。

表2 土壤全氮含量估测最优模型

3 讨论

3.1 光谱预处理对建模精度的影响

建模时将光谱R进行预处理可消除土壤类型（质地、颗粒大小等）及所处环境（温度、湿度等）对建模效果的影响，并适当提高模型的预测能力［27-28］。徐永明等［29］运用一阶导数（FDR）、倒数（1/R）、倒数对数［lg（1/R）］、波段深度4种数学变换后的光谱R与总氮含量进行分析，发现FDR和lg（1/R）变换后的回归和验证精度较高。陈红艳等［30］利用遗传算法结合偏最小二乘法对光谱的5种数据变换分别建模，发现反射率的一阶导数表现最佳。Zornoza等［31］将光谱数据进行多元散射校正和一阶微分处理后，建立的模型精度有明显提高。本研究结果与上述研究结果基本一致，本文利用R及FD、1/R、lgR和CR 4种变换后的光谱R数据进行建模，FD变换后模型的精度较低，可能原因是一阶微分在放大光谱特征波段的同时会放大噪声和无关因素的干扰，这在一定程度上也会降低建模精度，而其他数据变换在建模中对建模精度都有不同程度的提高，更能反映出土壤全氮含量的变化特征。

3.2 不同建模方法比较

土壤养分含量的高光谱估测模型主要有线性模型和非线性模型，合理选择建模方法是提高反演精度和效率的重要步骤。PLSR方法借鉴了主成分分析、典型相关分析和普通多元线性回归3种分析方法的优点［32］，较好地解决了样本数少于变量数等问题。王海江等［33］研究了基于特征波段建立的PLSR、SVM和SMLR模型，发现PLSR模型精度最高。刘秀英等［34］运用相关分析和偏最小二乘回归建立的黄绵土土壤全氮预测模型可对0～40 cm土壤全氮进行有效预测。而在本研究中，PLSR模型的精度却为最低，这可能是研究地域和土壤类型差异较大，总体缺乏代表性，土壤光谱存在较大的差异性，而且PLSR属于线性回归模型，而全氮含量跟光谱反射率是一种非线性关系，因此无法对全氮含量的非线性特征进行表征，从而难以保证估算结果的精确性和可靠性。代希君［35］利用ENVI 5.1将高光谱数据转换为多光谱数据，采用PLSR和SVM建立土壤盐分反演模型，结果发现SVM模型反演精度优于PLSR模型。刘焕军等［36］利用RF构建的基于影像波段和光谱指数的土壤有机质含量预测模型精度R2为0.69。王金凤等［37］运用RF、SVM、PLSR 3种方法进行元素含量与光谱变量建模后，发现基于二阶微分变换的RF准确度最高。为进一步提高模型精度，鉴于以上研究结果，本研究采取了非线性建模方法SVM和RF建立全氮含量估测模型，发现SVM建模精度较PLSR有小幅度的提高，而RF较PLSR建模精度有大幅度的提高，由于RF具有稳定性高、数据适应能力强、抗噪声能力强、在处理大数据集时预测精度高且不易产生过拟合等优点［18-19］，因此利用RF模型可有效提高模型预测精度和稳定性。

4 结论

根据不同等级土壤全氮含量光谱曲线得出，各曲线走势基本一致，在近红外波段的1415、1920、2220 nm处有明显的吸收特征。对比反射率曲线得出，在580～2400 nm内R随土壤全氮含量的增加而增大。

对土壤光谱R进行一定的数学变换，可提高土壤全氮和土壤光谱R的相关性，本研究选取的连续统去除变换明显提高了光谱与土壤全氮的相关性，相关系数最大，达到了0.43，更能反映土壤全氮含量变化特征。

RF模型在预测土壤全氮含量的过程中具有较高的估测精度，其整体预测精度要高于PLSR和SVM模型，可以对土壤全氮含量进行精确估测；SVM模型的估测精度虽然高于PLSR模型，但SVM和PLSR模型只能对土壤全氮含量进行粗略估测。对光谱数据进行数学变换后建模，除一阶微分变换外，其他数据变换均对模型精度有不同程度的提高。RF模型无论是分区建模还是全区建模，模型在各种数据变换之后预测精度差异性较小、模型结果均匀、稳定性高、适用性好。分区最优模型的精度要高于全区最优模型，但分区模型差异性明显，而全区模型综合了各地区土壤类型的差异，模型的稳定性较高，在进行分区建模时可通过增加样本数来提高模型的精确性和稳定性。