引入调制因子的单相电压型逆变器模型预测控制策略研究
2022-03-04孙乙巧王钰妍陈奕甫
孙乙巧,王钰妍,陈奕甫
(上海电力大学 电子与信息工程学院,上海 200090)
模型预测控制策略由于建模方法直观、控制策略灵活,广泛应用于三相逆变器控制中。文献[1]提出一种针对三相并网逆变器的预测模型电流控制方法,无法直接运用到单相逆变器控制中。文献[2]提出单相电压调制的评价函数中含有加权系数会对输出电压THD和平均开关频率产生影响。故本文通过建立单相逆变器输出端滤波元件LC在固定坐标系下的系统离散时间模型。根据电压面积等效原则,将调制因子m(k)引入评价函数,对评价函数无差拍控制得到m(k)因子电压调制表达式。为了进一步提高m(k)因子的自适应性和鲁棒性,对m(k)引入控制加权矩阵和反馈矩阵,提高整机的稳态性能。
1 单相逆变器模型预测控制策略
1.1 单相逆变器预测控制数学模型
典型单相逆变器拓扑结构如图1所示。
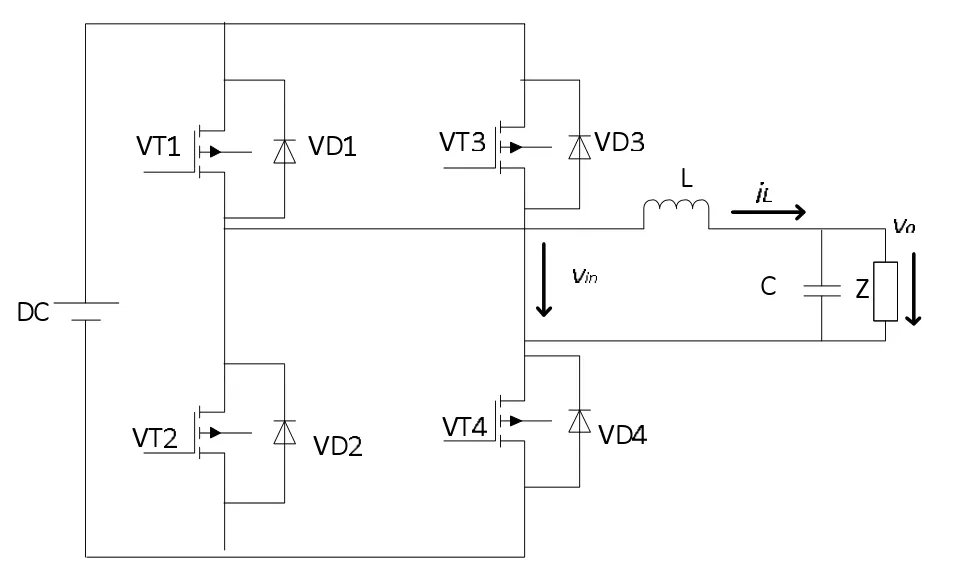
图1 单相逆变器模型
其中:z为逆变器的输出端负载;VT1、VT2、VT3、VT4为开关管;VD1、VD2、VD3、VD4为反并联二极管;L、C为滤波电感、滤波电容;DC为供电电源。
根据图1滤波电感、电容对单相逆变器建立系统模型,推导出系统输出端公式如下:

对系统输出电压、电感电流做二步预测得到系统模型为:
则对于逆变器桥臂电压而言,根据电压面积等效原理可以得到:

将式(2)、(6)带入式(4)得到输出电压的两步预测模型:
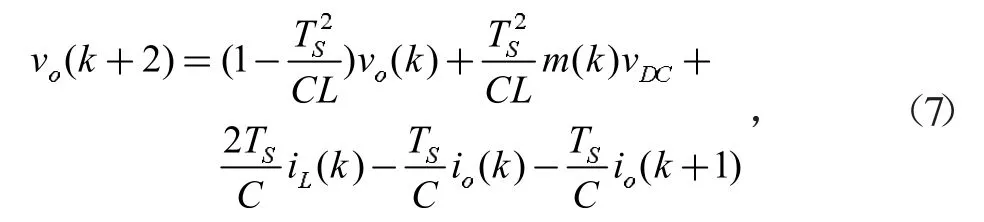
式中:TS为控制周期,m(k)为调制矢量因子,vo(k)为电压源输出电压,iL(k)为电感电流,io(k)为电压源输出端电流,io(k+1)为输出电流预测值,VDC为直流供电电压。
由于vo(k+2)中含超前预测项io(k+1),根据拉格朗日外推公式可以求得三阶io(k+1):

为了实现输出电压无差拍,以及避免对权重系数的选取,不考虑约束条件的情况下,在固定坐标系下将调制因子m(k)引入评价函数中,故得到评价函数为:

式中:v*o(k+2)为参考电压;vo(k+2)为两步预测输出端电压;J为评价函数符号。
2.2 系统控制策略
由于m(k)受多变量影响,在研究其控制过程时只考虑主要影响变量。据式(9)、(10)可以认为m(k)与v*o(k+2)实现无差拍即利用期望电压vREF替代m(k),不考虑系统模型失配问题,只研究输出加权矩阵GQ、滤波器GF对系统影响,其z域模型关系进行简化为式(12)、(13):


式中:GQ(z)是输出加权矩阵的z域传函;GF(z)是滤波器的z域传函。滤波器及误差补偿反馈F至少为一阶延时反馈即反馈对角矩阵阶数n=2。
虽然选择适当阶数的拉格朗日外推公式可以一定程度改善m(k)超前预测影响,但是考虑到提高控制系统的稳定性,需要设置控制加权矩阵Q。根据系统是完全能观且完全能控,状态方程系数矩阵非奇异,控制加权矩阵的优化时域P=n+1至少设为3阶矩阵。
进一步考虑,控制加权矩阵的阶数越高,输出电压动态响应过程越快,但对提高输出电压THD,综合单片机计算空间和输出电压动态响应过程,可令P=4。控制策略如图2所示。

图2 模型预测控制框图
2 实验验证
为验证本文提出控制策略的可行性和有效性,搭建单相H桥逆变器实验平台,控制和采样系统使用DSP28069控制芯片完成,MOS管选用意法STP30NF20,开关控制频率20 kHz,控制方式为双极性倍频,滤波电感1 mH,滤波电容10 uF。测试m(k)控制算法电压稳态与动态响应能力的实验波形如图3所示。
图3(a)为纯阻性负载时输出电压稳态波形,当输出电压稳定时m(k)调制方式的电压谐波含量为0.9%,相较于传统MPC控制策略2.23%谐波含量、PR控制2.6%的谐波含量,可以看出m(k)调制方式能维持较好的谐波含量;图3(b)纯阻性负载时输出电压动态响应过程,其调节时间分别为4.75 ms、相较于PR调制20.35 ms的调节时间可以看出m(k)因子具有较好的动态响应;图3(c)为纯阻性负载和阻感性负载稳压实验波形可以看出当负载波动时输出电压仍可以维持稳定。
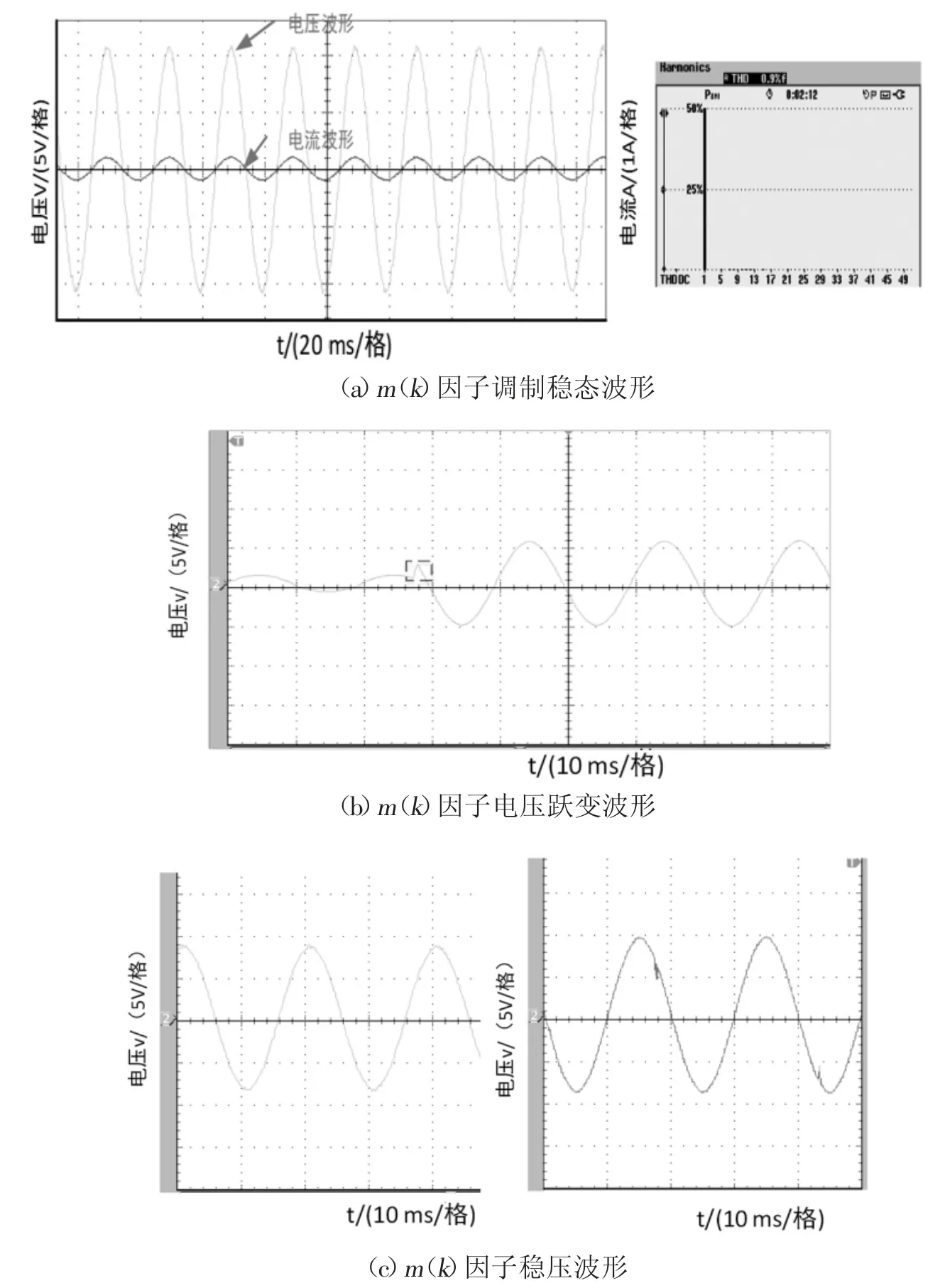
图3 实验波形
实验结果说明该控制方案可以实现电压稳定,验证了其可行性。从动态实验波形可以看出其具有较快的动态响应,验证了本文所提出控制算法的有效性。
3 结论
理论与仿真表明了基于模型预测控制理念的m(k)因子调制策略可以维持电压稳态,并且具备良好的动态性能,通过实验证实了该算法实际运行中的可行性和有效性。
