腐蚀近海桥墩十字形双向拟静力试验及损伤分析
2022-03-04袁文厅齐燕军方庆贺
袁文厅,齐燕军,方庆贺
(1. 中国矿业大学力学与土木工程学院,江苏,徐州 221116;2. 哈尔滨工业大学(威海),海洋工程学院近海结构研究中心,山东,威海 264209)
随着“海洋强国”战略和“一带一路”倡议的持续推进,我国的桥梁建设从内陆向海洋铺展,近海桥梁的建设规模得以迅速扩大[1-2]。受海洋腐蚀环境影响,近海桥梁的服役安全遭受严峻挑战。对于位处地震多发地区的近海桥梁,墩柱这一关键受力构件在役期间因持续腐蚀所致承载力和延性的降低[3]、刚度的减小[4]和耗能能力的减弱[5],是引起整个桥梁结构震损破坏的重要原因。因此,开展腐蚀墩柱的地震损伤研究非常必要。
单向拟静力试验是目前用于研究腐蚀墩柱地震损伤性能的常用手段。Meda 等[6]对2 个矩形截面RC 柱进行了单向拟静力加载试验。结果发现,当柱的腐蚀率为20%时,其极限承载力和变形能力较未腐蚀柱分别降低了30%和50%。Rajput 和Sharma[7]开展的RC 柱拟静力试验结果表明,腐蚀作用下柱的位移延性和曲率延性降低。基于RC 方柱的单向低周往复加载试验结果,牛荻涛等[4]发现腐蚀率和轴压比是影响RC 柱地震损伤的主要因素。针对非均匀腐蚀近海桥墩的地震损伤问题,苑溦[8]和Zhou 等[9]开展了单向拟静力试验研究。结果发现:腐蚀近海桥墩在地震作用下的塑性损伤区域从墩底向浪溅潮差区转移;非均匀腐蚀作用会增大试件的自振周期和阻尼比。
在地震作用下,墩柱会出现轻微、中等、严重和倒塌等不同损伤状态。为定量评估墩柱的地震损伤,Su 等[10]基于钢筋和混凝土应变状态建立了材料层面的损伤模型。然而,该类损伤模型不能直接用于反映承载力和变形等宏观力学性能,为实际工程操作带来不便[11]。针对该研究不足,部分学者提出了基于变形[12]、刚度[13]和耗能[14]等的单一损伤指标模型。此类损伤模型尚不能综合反映地震往复作用下结构的累积耗能和塑性变形性能。针对该问题,Park 等[15]提出了基于变形和能量耗散的Park-Ang 双参数损伤模型,该模型简洁实用,成为地震工程研究领域应用广泛的损伤模型之一。Wang 等[16]采用Park-Ang 损伤指标建立了基于性能的桥梁抗震设计方法。在Park-Ang双参数损伤模型基础上,国内学者引入了有效耗能因子[17]和能量项加权因子[18],建立了能更准确反映墩柱损伤进程的双参数损伤模型。其他学者通过修正变形项和能量项的计算公式[19-20],给出了适用于空心桥墩[11]、型钢混凝土异形柱[21]和腐蚀钢框架柱[22]的双参数损伤模型。考虑实际地震作用的多维特性,部分学者基于Park-Ang 双参数模型研究了双向地震作用下墩柱的损伤指标。其中,Qiu 等[23]开展了6 种加载路径下的RC 柱拟静力试验,计算了双向加载作用下RC 柱的X和Y方向的损伤指标,并采用两个方向的损伤指标之和评估柱的双向地震损伤。结果发现,在相同位移等级下,双向加载柱的损伤指标大于单向加载柱。Rodrigues[24]发展了可考虑双向地震作用不利影响的RC 柱地震损伤指标计算方法,对比分析了不同双向加载路径下柱的损伤指标差异性,其结果与观察到的试验现象吻合较好。
综上所述,现有研究主要集中于腐蚀墩柱的单向地震损伤,少数学者对未腐蚀墩柱的双向地震损伤进行了探索性研究,个别学者基于矩形双向拟静力试验[25],研究了腐蚀墩柱的滞回性能并定性分析了其双向地震损伤演化趋势,但除矩形外的其他双向加载路径下的腐蚀墩柱滞回性能有待研究,损伤程度的量化方法仍较为匮乏,该现状导致研究人员不能深入认识腐蚀桥墩在遭遇多维地震作用时的结构损伤特性。
鉴于此,本文以近海特有的立面非均匀腐蚀RC 桥墩为研究对象,设计未腐蚀和腐蚀墩柱试件各1 个,开展十字形双向拟静力试验,比较分析两个桥墩的承载力、变形能力、刚度退化及累积耗能的差异性,基于试验现象及Park-Ang 双参数模型,研究双向拟静力作用下未腐蚀和腐蚀墩柱的损伤演化规律。
1 试验概况
1.1 试件设计
依据《公路桥梁抗震设计细则》[26]中桥墩的配筋率和体积配箍率要求,并考虑试验设备能力,设计几何尺寸及配筋相同的桥墩试件A1 和A2(图1)。试件总高度为3350 mm,加载端头尺寸为700 mm×700 mm×450 mm,其上预留4 个直径为75 mm 的锚孔,用于连接试件顶端与千斤顶,墩身高度和截面边长分别为2300 mm 和540 mm,承台尺寸为1400 mm×1400 mm×600 mm,其上预留4 个直径为110 mm 的锚孔,以将试件锚固于实验室刚性地面。试件保护层厚度为25 mm。试件选用C30 商品混凝土进行浇筑,其立方体抗压强度平均值为31.1 MPa,可算得圆柱体抗压强度约为24.9 MPa。纵筋采用HRB335 级钢筋,其屈服强度和极限强度分别为400 MPa 和577 MPa。箍筋采用HPB235 钢筋,屈服强度和极限强度分别为247 MPa 和394 MPa。为获得墩柱试件的腐蚀程度分布,对主筋按逆时针方向从1~24 进行编号(图1)。
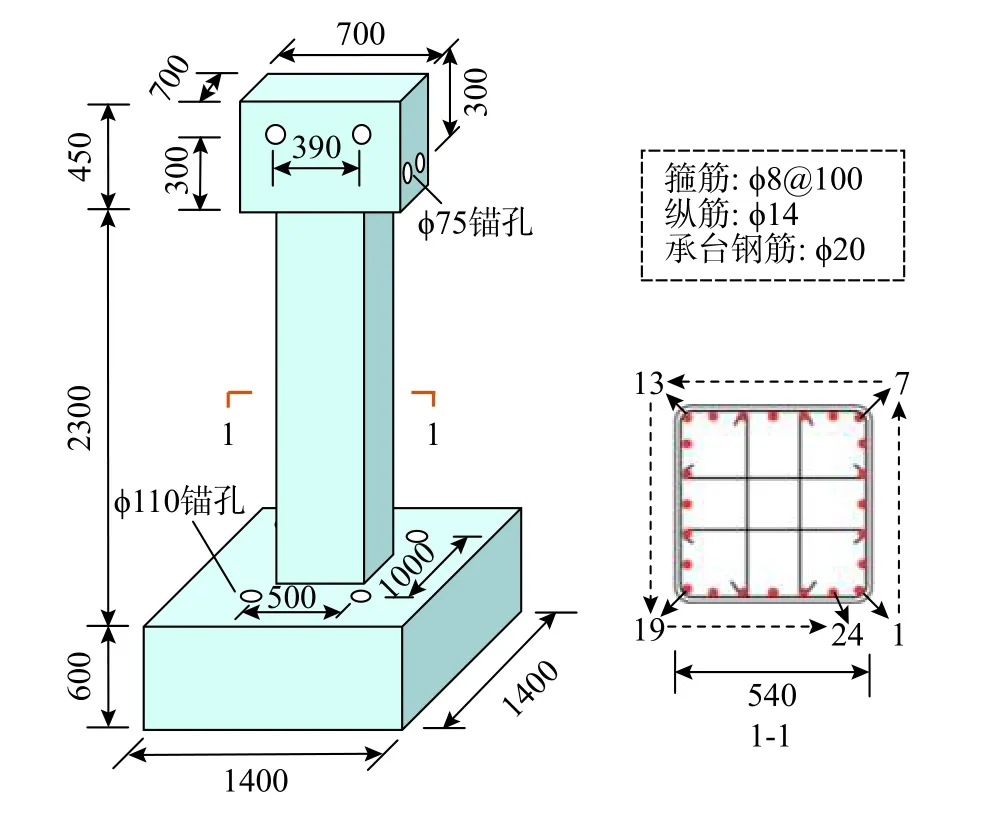
图1 试件几何尺寸及钢筋布置 /mmFig. 1 Dimensions and reinforcement details of specimens
1.2 试件加速腐蚀
近海桥墩具有典型的分区非均匀腐蚀特性,墩身浪溅区和潮差区腐蚀最为严重,这对桥墩的抗震性能极为不利[25]。为模拟该非均匀腐蚀现象,对桥墩试件A2 承台上方500 mm~1000 mm 高度范围进行电化学加速腐蚀(图2(a))。墩柱中纵筋和箍筋腐蚀时长相同,所有纵筋都连接通电导线,以防某根钢筋锈断影响腐蚀进程。腐蚀电路见图2(b)。已有研究[27]表明,加速腐蚀电流密度不应大于500 µA/cm2。基于此电流密度限值并考虑试验进度,将试件A2 的腐蚀电流密度设计为450 µA/cm2,纵筋的目标腐蚀率设计为25%。由于纵筋和箍筋接触,可将其整体看做串联体系,则所需施加电流为电流密度与腐蚀区域纵筋和箍筋的总表面积的乘积,其值为3.7 A。基于法拉第定律(式(1))[28]可计算出试件A2 达到目标腐蚀率所需通电时长为55 d。
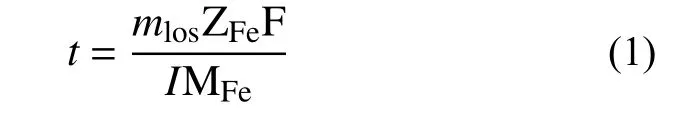
式中:t/s 为通电时长;mlos/g 为钢筋预期质量损失;ZFe为铁元素的化合价,取值为2;F 为法拉第常数,取值为96 485 (A·s)/mol;MFe为钢筋摩尔质量;I为腐蚀电流。试件A1 不腐蚀,用作对比分析。
腐蚀完毕后拆除水槽,得到试件A2 的腐蚀形态见图2(c)。由图可见,试件的混凝土表面出现大量红褐色锈蚀产物,其主要集中于锈胀开裂位置附近。拟静力加载结束后,从试件A2 中取出位于腐蚀区的长度为50 cm 的部分纵筋、截断后的部分箍筋(图3(a)),并在酸洗除锈后对两类钢筋进行称重,从而计算出腐蚀钢筋的质量损失率。其中,24 根纵筋的编号和质量损失率的关系如图3(b)所示。由图3 可知,纵筋和箍筋的腐蚀具有明显的非均匀性。试件A2 所有腐蚀纵筋和腐蚀箍筋的质量损失率平均值分别为24.15%和52.33%。

图2 桥墩试件加速腐蚀Fig. 2 Accelerated corrosion of specimen

图3 纵筋与箍筋腐蚀Fig. 3 Corrosion of longitudinal reinforcement and stirrups
1.3 双向拟静力试验加载方案
试验在北京工业大学城市与工程安全减灾教育部重点实验室进行,加载方式如图4 所示。试件通过4 根高强螺杆固定于实验室地面。试件顶端与3 个动力千斤顶相连,并利用东、北两面反力墙和反力横梁施加水平双向荷载和竖向荷载。为实现水平双向往复加载,反力横梁和竖向千斤顶之间通过水平双向滑板进行连接。试验过程中,数据采集频率设置为1 Hz。

图4 试件加载装置Fig. 4 Test setup of specimens
首先通过竖向千斤顶施加轴力(550 kN)并保持恒定,然后进行十字形水平双向往复位移加载。加载制度(图5)设计为:X方向位移幅值采用5 mm、10 mm、15 mm、25 mm、35 mm、45 mm、55 mm、65 mm 和80 mm,当X方向位移幅值小于15 mm 时,每级位移加载1 次,加载速度设定为0.1 mm/s;当位移幅值大于等于15 mm 时,每级位移循环加载2 次,加载速度设定为0.3 mm/s。Y方向位移幅值为X方向的0.8 倍。当试件的水平荷载下降到承载力的85%以下,即认为试件达到破坏状态,停止加载。

图5 双向十字形加载制度Fig. 5 Bidirectional cross-shaped loading pattern
2 试验结果对比分析
2.1 荷载-位移滞回曲线
图6 给出试件A1 和A2 在X和Y方向的荷载-位移滞回曲线,由图可知:

图6 试件的荷载-位移曲线Fig. 6 Load-displacement curves of specimens
1) 当试件A1 的位移等级不超过15 mm 时,其残余位移和滞回环面积均较小,试件无明显损伤。随着位移等级增大,试件A1 在两个方向的残余变形增加,滞回曲线变得饱满,且正负加载方向大致对称。当X方向位移幅值增大至65 mm时,试件的强度出现一定程度下降。试件强度的降低与墩底塑性铰区的混凝土压碎、纵筋压屈或断裂等有关[29]。
2) 与试件A1 相比,试件A2 的滞回环面积总体减小,加载过程中的承载力很快达到最大值,随着位移等级继续增大,强度快速下降。表明腐蚀钢筋、锈胀开裂混凝土保护层和锈蚀箍筋约束核心区混凝土的力学性能退化,加速了试件损伤进程。由于纵筋和箍筋腐蚀不均匀(图3),试件A2 在相同正向位移和负向位移值下,对应的推力值和拉力值存在显著差异,引起试件较为明显的滞回曲线不对称现象,其中,X方向的正向峰值荷载比负向峰值荷载小18.3%。
3) 试件A2 的滞回曲线捏拢现象比A1 更明显,这与Kivell 的研究结论一致,其原因为腐蚀钢筋和混凝土间的黏结性能退化引起了A2 更显著的界面滑移[30]。
2.2 强度和变形能力
将滞回曲线中每一位移等级对应的峰值点提取出来,得到骨架曲线示于图6。由图可知,试件A1 的骨架曲线下降段总体比试件A2 缓和。基于骨架曲线,可计算得到试件的荷载-位移特征点,如表1 所示。基于表1,可计算试件的正向和负向峰值荷载的平均值,以表征其极限承载力。其中,试件A1 的X向和Y向极限承载力分别为161.49 kN 和170.15 kN,试件A2 的X向和Y向极限承载力分别为137.62 kN 和121.25 kN,相比于A1 降低了14.78%和28.74%。在表1 中,试件A1 的Y负向极限位移大于49.79 mm,对应的位移延性系数大于1.94。这是由于:在整个加载过程中,试件A1 的Y负向最大位移为49.79 mm,试件未达到水平荷载低于其峰值荷载的85%这一极限状态。同理,试件A2 的Y正向极限位移和位移延性系数分别大于36.6 mm 和2.30。
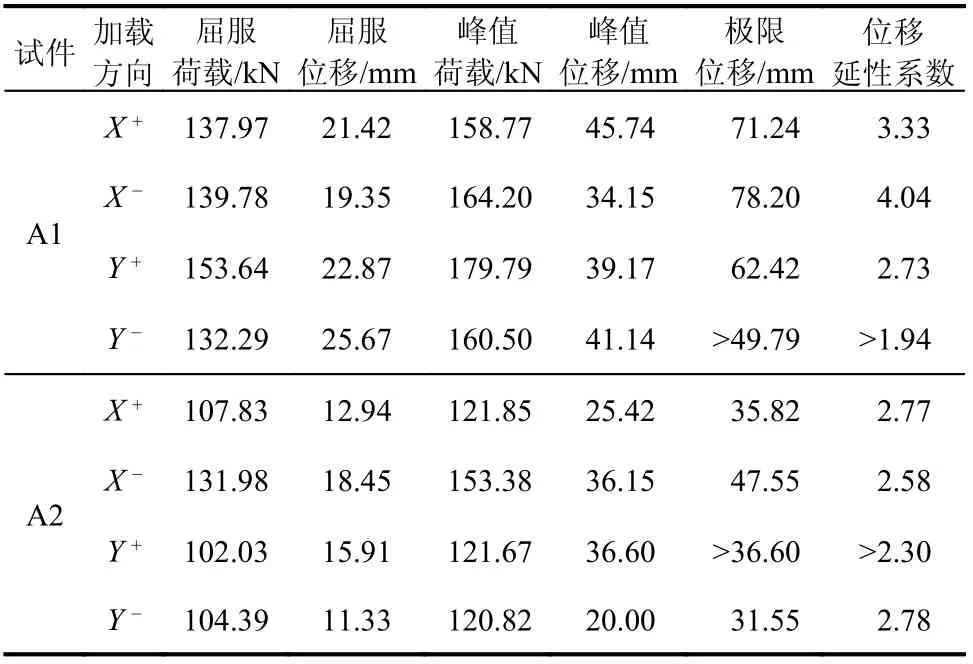
表1 试件荷载-位移曲线特征点Table 1 Characteristic points of load-displacement curves of specimens
2.3 耗能性能
滞回环围成的面积可表征试件的耗能能力。在双向加载工况下,分别对X和Y方向每个位移等级下的滞回环面积进行累加,得到两个方向的累积耗能Ex和Ey,总的累积耗能Et计算如下:

试件A1 和A2 的累积耗能如图7 所示。由图可知,腐蚀率对试件耗能的影响规律为:

图7 滞回耗能Fig. 7 Hysteretic energy dissipation
1) 当墩顶位移小于40 mm 时,腐蚀试件A2和未腐蚀试件A1 的累积耗能值相差不大,A2 略大于A1,在其他学者的研究中也发现类似现象[31]。出现该现象的原因可能为:在该位移等级下,试件A2 出现了塑性变形耗能能力,而试件A1 塑性变形较小,耗能能力较弱。
2) 随着位移进一步增大,腐蚀试件的混凝土和钢筋发生明显损伤,对耗能的贡献减小,累积耗能增长速率减缓;而未腐蚀试件的累积耗能随着塑性变形的增大而继续显著增加。试件A1 和A2 的累积耗能曲线也因累积耗能增长速率的差异出现了相交的现象。
3) 在加载结束时刻,试件A2 的总耗能比试件A1 降低了55.74%。因此,腐蚀作用会显著降低试件达到破坏状态的耗能能力。
2.4 刚度退化
割线刚度可反映试件在反复荷载作用下的刚度退化规律,采用式(3)定义试件刚度退化率:

式中:Ki为第i次位移等级下的刚度; ±Fi为第i次位移等级对应的正、负向峰值力; ±δi为正、负向峰值力对应的位移值。
试件A1 和A2 在X和Y方向的割线刚度与位移的关系见图8。该图呈现以下规律:

图8 刚度退化Fig. 8 Stiffness degradation
1) 随着位移加载幅值增加,两个试件的的刚度均呈现出先迅速后缓慢的指数型下降趋势,表明了试件的损伤不断累积。
2) 在相近的位移加载等级下,腐蚀试件的割线刚度小于未腐蚀试件。该现象的原因为:在相同的位移等级下,腐蚀试件的材料性能退化,导致其滞回环的峰值荷载小于未腐蚀试件。
3) 对于同一试件,其在X和Y方向的割线刚度退化率基本相当。
3 损伤演化分析
3.1 试件损伤进程和破坏特征
3.1.1 试件A1 试验现象描述
当X=5 mm、Y=4 mm 时,试件东面基础以上50 cm 位置处出现肉眼可见的裂缝;试件北面和南面也有发丝般裂缝出现。随着位移等级加载至X=15 mm、Y=12 mm 时,墩身四面细小水平裂缝的数量显著增加。当X=35 mm、Y=28 mm 时,墩身裂缝宽度明显增大。例如,在试件东面基础以上约20 cm 位置处的一条裂缝变得清晰可见。当试件加载到X=45 mm、Y=36 mm 时,试件东面及东南基础以上20 cm 位置处裂缝宽度大于0.5 mm,裂缝处出现混凝土轻微掉皮现象。试件在加载过程中的典型裂缝分布见图9(a)。加载结束时,试件东面、东北角、西北角以及东南角等发生了严重的混凝土保护层压溃现象;在试件东南角出现了纵筋压屈现象。试件的破坏区域高度约为30 cm,最终破坏形态如图10(a)所示。

图9 混凝土裂缝发展Fig. 9 Evolution of concrete cracks
3.1.2 试件A2 试验现象描述
当X=5 mm、Y=4 mm 时,试件北面基础以上约60 cm 及东面基座以上30 cm、60 cm 位置处出现了多条发丝般水平裂缝;试件南面基础以上约15 cm、30 cm 和50 cm 位置处出现3 条轻微水平裂缝。当X=15 mm、Y=12 mm 时,试件东面和北面的裂缝已明显增多,东面基础以上60 cm 高度处的水平裂缝宽度已接近0.5 mm;试件南面基础以上约50 cm 高度处也有发丝般水平裂缝。当X=25 mm、Y=20 mm 时,试件南面基础以上约60 cm 和东面基础以上约60 cm 处的裂缝相互贯通,裂缝宽度达到1 mm,试件北面基础以上约50 cm 位置处的水平裂缝变得清晰。当X=35 mm、Y=28 mm 时,墩身东面约60 cm 高度处的裂缝宽度已达到约3 mm,此时试件损伤严重。试件在加载过程中的典型裂缝分布见图9(b)。加载结束时,墩身四面的腐蚀区域发生了严重的混凝土压碎剥落现象;墩身南面腐蚀区出现了纵筋压屈现象。试件承台顶面以上45 cm~85 cm 高度区间发生严重破损现象,最终破坏形态如图10(b)所示。

图10 最终破坏状态Fig. 10 Final failure modes
3.1.3 试件A1 与A2 试验现象对比
两个试件表面主要出现弯曲裂缝,但裂缝发展过程及最终破坏模式不同,具体表现为:
1) 试件A1 裂缝分布高度范围广且分布密集;试件A1 墩底区域的裂缝宽度随弯矩增大而增大;试件A2 裂缝分布较为稀疏,且主要集中于腐蚀区,这表明,腐蚀钢筋和混凝土的性能劣化导致腐蚀区截面开裂荷载的降低。腐蚀区裂缝宽度随位移加载等级的增加而增大。
2) 在达到破坏状态时,试件A2 的混凝土保护层大面积剥落现象明显于试件A1。其原因为:在锈胀力作用下,试件A2 的保护层与核心区混凝土之间发生剥离,混凝土保护层抗压强度因锈胀裂缝的出现而发生退化。
3) 箍筋锈断现象的出现,削弱了其对纵筋屈曲变形的约束能力,因此腐蚀试件A2 的纵筋压屈现象也比未腐蚀试件A1 明显。
3.2 基于Park-Ang 模型的损伤分析
为了进一步研究双向地震作用下墩柱的损伤程度,本文在现有Park-Ang 双参数模型的基础上,考虑腐蚀影响,进行试件的损伤分析。
3.2.1 现有Park-Ang 双参数地震损伤模型
现有双参数地震损伤模型中,Park-Ang 模型被广泛应用[15],其采用线性组合的方式考虑归一化变形和归一化累积耗能的影响,见下式:

式中: ρw为体积配箍率;v为试件轴压比;ωt为纵筋拉伸率。
3.2.2 双向地震损伤模型的改进及参数确定
基于Park-Ang 单向地震损伤模型,文献[24]建立了考虑加载路径的双向地震损伤指标计算公式并进行了试验验证,本研究以此为基础,进一步建立考虑腐蚀影响的桥墩双向地震损伤指标Db(η),见以下两式:

由式(6)和式(7)可知,不同加载方向下的屈服点和极限点的确定是计算腐蚀试件双向地震损伤指标的关键。考虑到不同方向单调加载试验数据的缺乏,本文基于文献[33]中已经验证的精细化数值模型,采用Pushover 分析方法获得屈服点和极限点数值。以试件A1 为例,其在某加载角度Pushover 下的荷载-位移曲线如图11 所示。基于该曲线,采用等面积法确定屈服点。此外,以文献[8, 34]的计算方法为基础,本文将极限位移定义为以下两者中的较小值:① 荷载达到峰值荷载的85%对应的位移;② 纵筋拉应变为0.6 倍极限拉应变时对应的位移。

图11 试件A1 在某方向下的Pushover 曲线Fig. 11 Pushover curve of Specimen A1 at a given direction
3.2.3 试件损伤分析
基于3.2.2 节方法,可计算双向加载下试件A1 和A2 的双向屈服力Fy,res及双向极限位移δu,res,结果如图12 和图13 所示。可以看出,腐蚀作用导致试件在不同加载方向的屈服荷载和极限位移的降低。基于此,由式(6)计算得到试件在不同位移等级下的损伤指标。为了验证该指标的合理性,将试件在4 个位移幅值下的损伤现象、文献[35]划分的损伤等级、本文损伤指标计算值、陈星烨等[35]和牛荻涛等[36]的双参数损伤指标范围进行对比分析,列于表2。由表2 可见,本文理论公式计算的损伤指标,结合牛荻涛等的损伤指标范围,可合理量化试件损伤状态,陈星烨等的损伤指标范围会高估损伤程度。由表2 可发现,两个试件的损伤指标都随着位移等级的增加而增大,且该变化趋势受腐蚀率影响显著。对应于4 个位移等级,腐蚀试件A2 经历了开裂、峰值和极限状态。当位移为45 mm 时,损伤指标大于1,试件A2 破坏,这与骨架曲线反映的承载力显著降低相对应。而对应于该位移,试件A1 的损伤指标仍然远小于1,试件的承载力未出现明显下降。可见,腐蚀作用减小了试件的塑性变形能力并加速了试件的破坏,导致腐蚀试件的损伤指标大于相同位移等级下的未腐蚀试件。
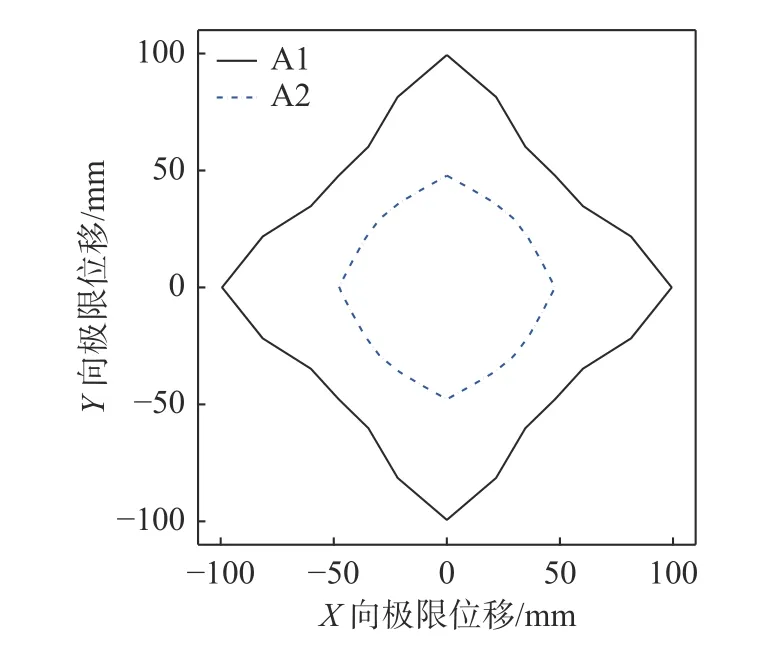
图12 双向屈服力Fig. 12 Bidirectional yielding force
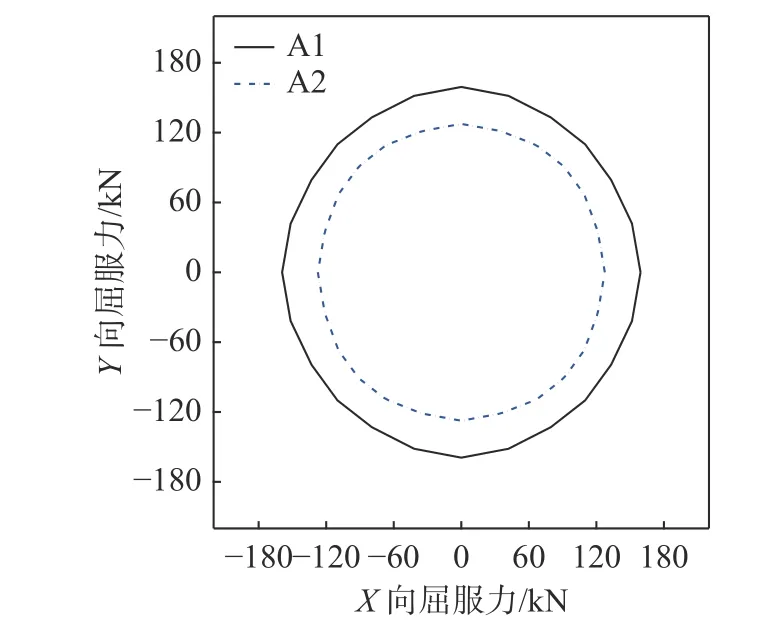
图13 双向极限位移曲线Fig. 13 Bidirectional ultimate displacement curve

表2 试件损伤指标计算结果对比分析Table 2 Comparison analysis of damage indexes of specimens
为了进一步直观的研究变形和耗能两个参数对结构损伤指标的影响规律,图14 给出了试件A1 和A2 的变形项(式(6)中第一项)在损伤指标中所占的百分比随墩顶位移的变化规律。由该图可知,桥墩的位移是其引起桥墩试件损伤的主因。在桥墩达到屈服状态前,变形项在损伤指标中所占的比重接近于100%,耗能的贡献几乎可以忽略。随着桥墩位移的增加,位移在损伤指标计算中所占比重减小,耗能项所占比重增加。随着墩顶位移的进一步增加,桥墩发生了严重的损伤破坏,耗能能力减小,使得位移所占比重又缓慢增加。以腐蚀桥墩A2 为例,当其墩顶位移为由14.5 mm 增大至45.2 mm 和61 mm 时,变形对损伤指标的贡献由93.3%先降低为83.1%后增大至85.0%。

图14 变形成分对损伤指标的贡献Fig. 14 Contribution of deformation to damage index
4 结论
通过2 个钢筋混凝土墩柱试件的十字形双向拟静力试验,对比研究了试件在腐蚀和未腐蚀情况下的滞回特性和损伤演化规律,主要结论如下:
(1) 在十字形双向加载作用下,未腐蚀桥墩的损伤过程及破坏模式与非均匀腐蚀桥墩有明显差异。在裂缝开展方面,未腐蚀桥墩的裂缝扩展慢、密集且主要分布于墩底区域,腐蚀桥墩裂缝扩展快、稀疏且主要分布于腐蚀区;在最终破坏方面,未腐蚀桥墩严重损伤区域高度为30 cm,而腐蚀桥墩的严重损伤区域高度增加到40 cm。
(2) 未腐蚀和腐蚀桥墩试件经历强度上升、稳定和退化3 个阶段,骨架曲线可等效为三折线,腐蚀桥墩试件的强度稳定段不明显且强度退化段陡峭。
(3) 在现有双参数双向地震损伤模型基础上,通过引入腐蚀率这一参数对该模型进行了修正,并给出了模型中双向极限位移和双向屈服力的计算方法。修正后的模型能合理反映腐蚀桥墩在双向地震作用下的损伤演化规律。
