基于有限元对沙发不同形状等节距蛇簧的力学分析

文/张小吉

沙发的舒适感来自软质材料的支撑。其软质材料按功能分为两种：一种提供柔软度，如包覆物中的发泡橡胶或其他软性材料；另一种提供弹性支撑，如座框中所设置的蛇簧、弹簧或弹性绳。目前，市场上使用较广且技术较成熟的沙发结构为配置多条蛇簧的一体化式座框（见图1）。蛇簧的母线结构形式分为3种：平状、弓状和圆弧状，峰形结构分为两种：矩形和圆形。

图1 蛇簧座框结构示意图

行业标准《软体家具 沙发》（QB/T 1952.1-2012）第5.5条对于沙发耐久性检验项目规定如下：“经各相应等级测试后，沙发座、背及扶手的面料应完好无损，面料缝纫处无脱线或开裂，垫料无移位或破损，弹簧无倾斜、无松动或断簧，绷带无断裂损坏或松动，骨架无永久性松动或断裂。”目前，在耐久性测试中，蛇簧断裂是主要的产品损坏形式，制造企业的解决办法是：在现有结构基础上增加多条蛇簧，以分散其下压力产生的压强，从而减少每条蛇簧的应力。但此种方式会增加企业成本。已有的相关研究有：张琳[1]等人对沙发弹簧坐垫结构进行了研究，以期得到座框的力学模型，为力学模型分析提供一些理论支持。王麒宇[2]等人利用有限元横梁模型搭载了一个立体的沙发框架，研究出了一种搭建沙发框架的简易方法。本文结合前人研究，尝试使用有限元分析技术来比较不同峰形的平状蛇簧在相同压下量作用下的受力情况，从而为沙发设计、蛇簧的制作和使用过程提供参考。

一、蛇簧模型与相关尺寸

本文研究的蛇簧是在国内沙发设计与制造过程中被广泛采用的平状圆形等节距蛇簧与平状矩形等节距蛇簧。为便于比较，本文中所选的模型总长均为550 mm，弹簧横截面均为直径3.50 mm的圆形，节距均为22 mm，峰高均为37 mm，具体参数见图2和图3。

图2 平状圆形等节距蛇簧模型与尺寸/mm

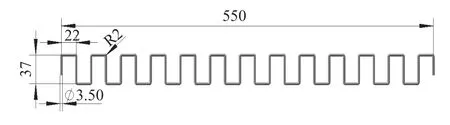
图3 平状矩形等节距蛇簧模型与尺寸/mm

二、分析过程

1. 设置材料参数

结合《冷拉碳素弹簧钢丝》（GB/T 4357-2009）的要求，弹簧材料设定为冷拉碳素弹簧钢丝，该种材料的物理参数为：弹性模量为201 GPa，泊松比为0.29，屈服极限为350 MPa[3]。

2. 边界条件和载荷条件

边界条件：蛇簧与框架通过弹簧扣连接（见图4）。在有限元分析中，模型两端的直线段分别约束3个方向的平动自由度和2个方向的转动自由度，即UX= 0，UY= 0，UZ= 0，ROTY= 0，ROTZ= 0。

图4 蛇簧与框架连接示意图

载荷条件：模型模拟实际使用过程中的工况，假设两种蛇簧分别受到相同的位移压下量UZ= –100 mm，作用位置为蛇簧长度方向中点处。

3. 结果分析

① 轴向力分布云图的比较

在仿真ANSYS软件中进行有限元分析来评估相关模型，其材料性能参数需符合上述材料物理参数的规定，其加载边界条件与载荷条件需符合上述边界和载荷条件的规定，以获得其轴向力部分的力分布云图。图5为平状圆形等节距蛇簧所受轴向力分布云图和局部放大显示区域。图6为平状矩形等节距蛇簧所受轴向力分布云图和局部放大显示区域。

当平状圆形等节距蛇簧中间位置受到的压下量为100 mm时，其最大轴向力为290 N，最大轴向应力为：σ=F/S=290/[π×（0.0035/2）2] =30.1 MPa，其中S为蛇簧截面积。

轴向应力分布详见图5–a。与受力方向平行的区域轴向应力最大，后逐步减少至受力方向垂直的蛇簧部分，轴向应力较大的位置主要位于平状圆形等节距蛇簧弧形段的峰顶处（见图5–b）。

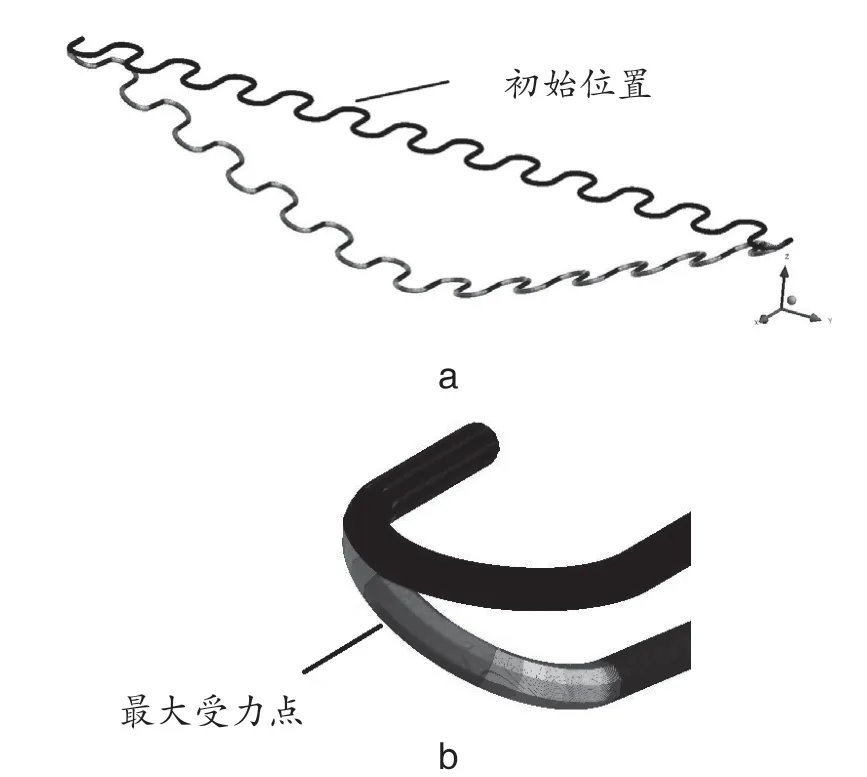
图5 平状圆形等节距蛇簧所受轴向力分布云图和局部放大显示区域

当平状矩形等节距蛇簧中间位置受到相同的压下量时，其最大轴向力为207 N，最大轴向应力为：σ=F/S=207/[π×（0.0035/2）2] =21.5 MPa。

轴向应力较大的位置主要位于平状矩形等节距蛇簧与受力方向平行的区域处，并且蛇簧与该部分的轴向应力趋于均匀一致（见图6–b）。

图6 平状矩形等节距蛇簧所受轴向力分布云图和局部放大显示区域

上述两种情况说明，在相同压下量为100 mm时，平状矩形等节距蛇簧受到的轴向应力最大值较平状圆形等节距蛇簧小，且最大应力位置均出现在与受力方向平行的区域中，两种蛇簧结构相较而言，平状矩形等节距蛇簧抗拉能力更优。在对轴向力分布云图进行比较时，我们可观察到，轴向力分布范围均集中在蛇簧与拉力方向平行的区域，平状矩形等节距蛇簧与平状圆形等节距蛇簧相比，平行于受力方向的受力长度之和较大，故平状矩形等节距蛇簧受到的轴向应力最大值较平状圆形等节距蛇簧小。

② 剪切力分布云图的比较

图7为平状圆形等节距蛇簧所受剪切力分布云图和局部放大显示区域。图8为平状矩形等节距蛇簧所受剪切力分布云图和局部放大显示区域。

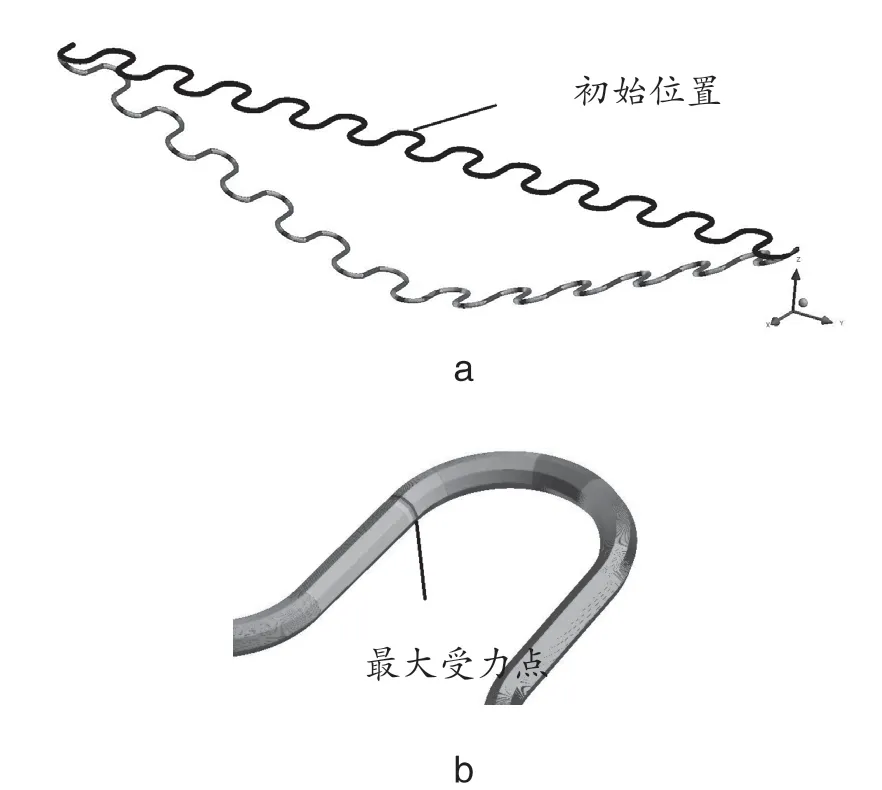
图7 平状矩形等节距蛇簧所受剪切力分布云图和局部放大显示区域

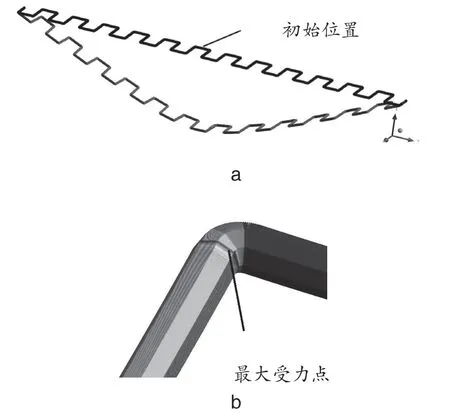
图8 平状矩形等节距蛇簧所受剪切力分布云图和局部放大显示区域

当平状圆形等节距蛇簧中间位置受到的压下量为100 mm时，其最大剪切力为474 N，最大截面剪切应力σ =F/S =474/[π×（0.0035/2）2] =49.3 MPa。剪切应力较大的位置主要位于平状圆形等节距蛇簧弧形段过渡到直线段的区域（见图 7–b）。

在相同压下量的情况下，平状矩形等节距蛇簧受到的最大剪切力为829 N，最大截面剪切应力σ = F/S =829/[π×（0.0035/2）2] =86.2 MPa。剪切应力较大的位置主要位于平状矩形等节距蛇簧的圆角区域（见图8–b）。

在相同压下量为100 mm的情况下，平状矩形等节距蛇簧受到的剪切应力最大，是平状圆形等节距蛇簧所受剪切应力的1.75倍。在剪切应力分析中，平状矩形等节距蛇簧相比平状圆形等节距蛇簧在转角处容易造成应力集中，也更容易造成失效。剪切应力集中产生的原因多数由受力物体的形状所导致，平状矩形等节距蛇簧在使用时，应特别注意弯角处剪切应力较大的问题。

三、结 论

本文主要分析了平状圆形等节距蛇簧和平状矩形等节距蛇簧在相同压下量100 mm情况下的受力分布，最后得出：两种不同结构的平状等节距蛇簧在相同压下量时，所受轴向应力和剪切应力的情况存在一定差异；两种不同结构的平状等节距蛇簧在相同的直径下，剪切应力和轴向应力此消彼长。相关人员需结合不同的设计、工况选取不同形状的蛇簧，从而增加沙发产品类家具的使用寿命。