塔式起重机臂架优化设计

马洪锋 颜 婷

江苏徐工工程机械研究院有限公司 徐州 221000

0 引言

臂架是塔式起重机（以下简称塔机）的主要承载结构件之一，其构造多样且受力复杂，其承载能力直接影响整机的起重性能与安全[1]。如图1所示，塔机臂架为典型的桁架结构，而局部稳定性是限制桁架臂承载能力的主要力学问题之一。

图1 塔机整体结构示意图

桁架臂属于格构式结构，在工作中容易发生屈曲破坏[2]。经研究发现，影响臂架临界载荷和临界应力的因素包括支撑方式、材料、截面惯性矩等[3-5]。当利用轴向受压构件稳定性公式计算桁架臂架弦杆稳定性时，弦杆的长度系数选取尤为重要[6]。在传统计算中忽略了腹杆抗弯对弦杆的限制作用，计算长度系数取值较大，由此计算得到的臂架承载能力低，限制了起重机的起重性能[7]。原本可满足强度的型材可能将不能满足要求，为此需要提高弦杆规格，最终导致材料浪费而不利于轻量化，故研究桁架臂屈曲稳定性尤为重要。

本文以某型塔机桁架臂为例，首先根据轴心受压的稳定性验算公式，对臂架进行稳定性分析；然后利用有限元方法对塔机臂架进行屈曲分析并结合试验，分析了不同初始缺陷、主弦规格、腹杆规格和跨数对桁架臂稳定性的影响，得到桁架臂的屈曲破坏载荷，以此优化臂架规格，实现塔机臂架轻量化设计。

1 屈曲理论分析

以某型塔机臂架为例进行稳定性分析。该臂架基本参数为：材料弹性模量E＝210 000 MPa，泊松比μ＝0.3，密度ρ＝7.85 g/cm3，弦杆材料为Q560，屈服极限σs＝560 MPa，臂架截面高度H＝1 085 mm，截面宽度W＝1 218 mm。

1.1 稳定性理论

GB/T 13752—2017《塔式起重机设计规范》给出了构件轴心受压的稳定性验算，构件的临界力为

式中：Ncr为构件的轴向临界压力，φ为轴心受压稳定系数，A为构件的毛截面面积，σs为构件屈服极限。

式中：λ为构件对通过形心轴的长细比，lc为构件的计算长度，r为构件对通过形心轴的回转半径。

构件计算长度为

式中：μ为计算长度系数。

回转半径为

式中：I为构件对通过形心的惯性矩，A为构件截面面积。

1.2 稳定性校核

以三角形截面形式为例，截面参数如图2所示。根据惯性矩定理，可得

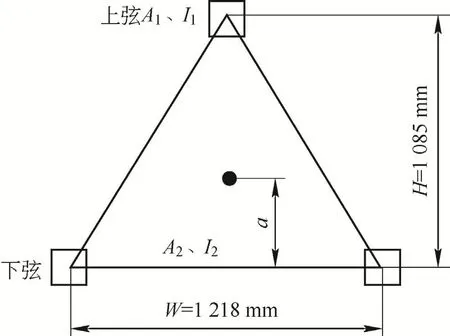
图2 臂架横截面尺寸示意图

式中：I为整体惯性矩，I1、I2分别为上下弦惯性矩，A1、A2分别为上下弦截面面积，H为上下弦截面中心距离，a为构件截面形心高度。

在校核整体稳定性时，按照一端固定一端悬臂处理，长度系数取2；弦杆单肢失稳校核取长度系数为1。通过计算，可得构件的临界应力为

传统稳定性理论计算忽略了腹杆抗弯对弦杆的限制作用，由此计算得到的桁架臂承载能力偏低，限制了臂架的起重性能。

2 臂架实例分析

2.1 有限元分析

臂架由空间方向不同的杆件焊接组成，建立有限元模型时，单元划分采用梁单元Beam 189，利用Ansys软件仿真分析横向均匀加载下起重臂的屈曲破坏情况。由分析可知，臂架2根下主弦在施加相同载荷时，臂架在XY(变幅）平面内有可能发生失稳，也可能在XZ(回转）平面内失稳。当臂架横向均匀加载时，上主弦杆受拉，2下主弦杆受压。由分析可知，屈曲破坏位置最终发生在下弦杆处，故只需对下弦杆进行贴片即可。

臂架由3节臂架组合而成，其中臂节1的长度L1＝10 000 mm、跨数n1＝7；臂节2的长度L2＝5 000 mm、跨数n2＝3；臂节3的长度L3＝1 500 mm、跨数n3＝2。定义主弦规格66 mm×4 mm，腹杆规格38 mm×3 mm，安全系数取1.34。横向加载时屈曲破坏应力图如图3所示。

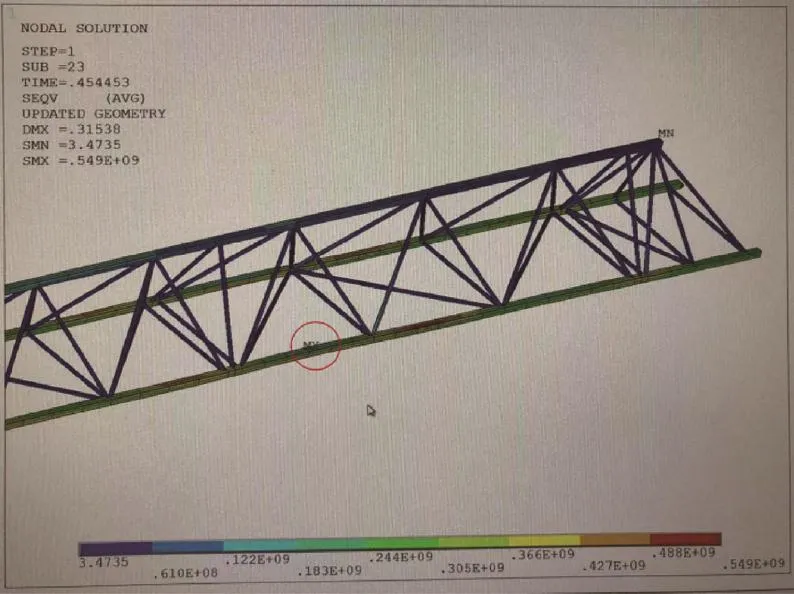
图3 横向加载时屈曲破坏应力图

分析不同初始缺陷系数下臂架结构屈曲载荷和临界轴应力，数据汇总如表2所示。由表2可知，初始缺陷系数对结构临界载荷和临界应力的影响非常明显，且桁架臂结构的最大承载能力和临界轴应力与初始缺陷呈非线性关系，初始缺陷系数越大，一阶屈曲破坏载荷和临界轴应力越小（见图4、图5）。当初始缺陷为0‰时，一阶屈曲破坏载荷为642 kN；当初始缺陷为0.5‰时，一阶屈曲破坏载荷为605 kN，下降了5.8%；当初始缺陷为1‰时，一阶屈曲破坏载荷为578 kN，下降了10%，说明初始缺陷的选取对桁架臂的承载能力影响很大。

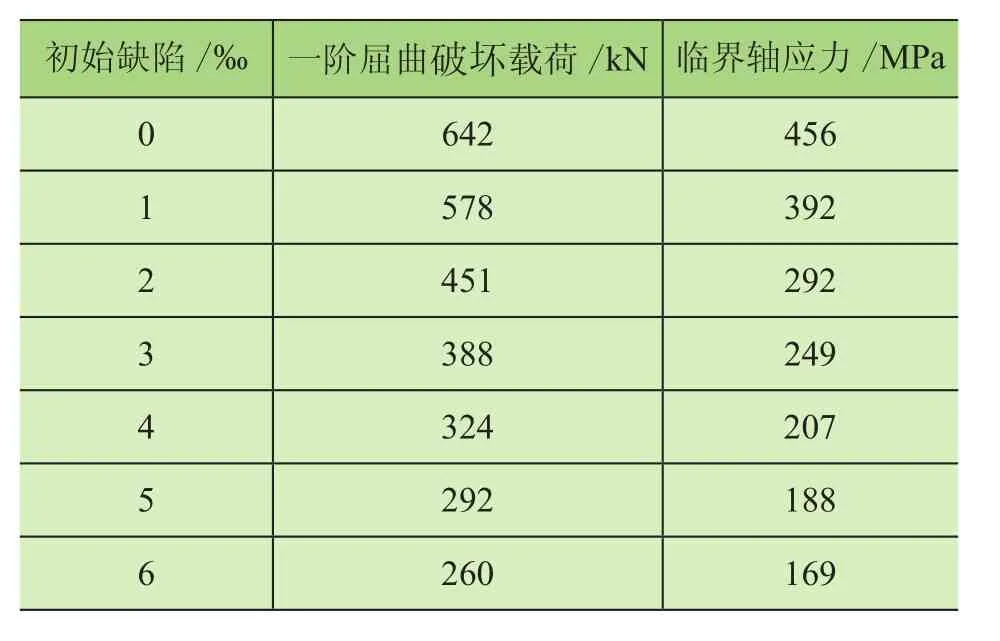
表2 不同初始缺陷臂架结构计算结果汇总

图4 一阶屈曲破坏载荷图

图5 临界轴应力图

2.2 臂架稳定性试验

对塔机臂架进行加载破坏试验，确定塔机臂架实际承载能力。试验时取臂架中3节臂组合进行稳定性分析，臂架安装如图6所示。臂架一端固定在试验平台上，另一端通过连接的作动器进行加载。试验臂架由3节臂架组合而成，其中臂节1的长度L1＝10 000 mm、跨数n1＝7；臂节2的长度L2＝5 000 mm、跨数n2＝3；臂节3的长度L3＝1 500 mm、跨数n3＝2。主弦规格66 mm×4 mm，腹杆规格38 mm×3 mm。进行图7所示初始缺陷测量，按照实测初始缺陷0.1%有限元计算，得到最大承载能力作为预测破坏载荷，并进行屈曲破坏试验，作动器水平放置进行轴向加载，直至加载至样品发生屈曲破坏为止，试验结束。

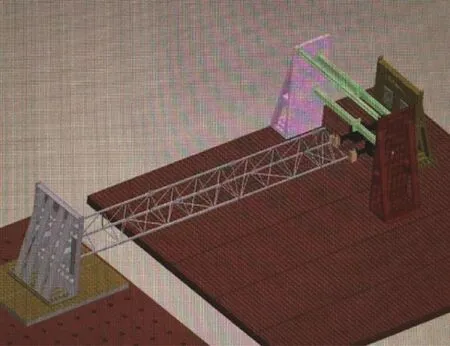
图6 塔机臂架试验安装示意图

图7 初始缺陷测量示意图

如图8所示，在横向均匀加载的条件下，共进行3次破坏试验，3次试验中臂架均发生了失稳破坏，试验结果显示臂架的屈曲薄弱点主要集中在第二节臂架下弦处，臂架破坏平面为XY(变幅）平面，与有限元分析结果一致。将解析计算破坏载荷及仿真结果和试验屈曲破坏载荷进行对比，如表3所示。

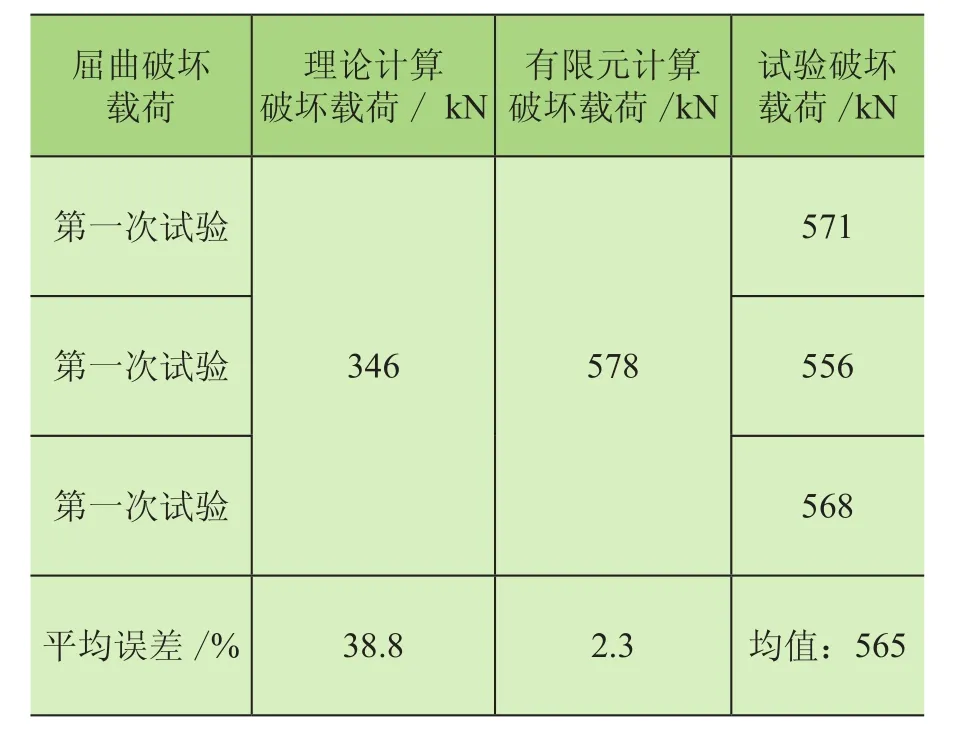
表3 臂架破坏载荷计算对比

图8 试验破坏情况示意图

由试验对比可知，按照规范计算得到的屈曲破坏载荷偏小，试验破坏载荷比按照理论规范计算得到的最大承载能力高出38.8%，说明按照规范计算得到的屈曲破坏载荷计算结果保守且偏差大，低估了塔机臂架的实际承载能力。试验破坏载荷和有限元计算结果很相近，误差约2.3%，且破坏位置与有限元计算位置一致，说明有限元方法计算得到的臂架极限载荷更接近实际，验证了有限元模型的正确性，为臂架设计提供参考。

3 尺寸优化

采用有限元法对塔机臂架标准节进行屈曲稳定性分析，分析主弦规格、腹杆规格以及跨数对桁架臂屈曲临界力影响。在此取臂架截面类型为三角形截面，臂架截面高度H＝1 085 mm，截面宽度W＝1 218 mm，臂长L＝10 000 mm，有限元计算选取初始缺陷为0.1%。由图9可知，跨数布置较多时，臂架结构趋于稳定，不易发生屈曲。随着弦杆跨数的增加，弦杆的屈曲载荷亦增大；然而，当跨数增加到7跨时，继续增大跨数对临界载荷的影响较小。图10显示了主弦规格和腹杆规格对臂架屈曲稳定性的影响，以7跨臂架为例，由于受主腹杆规格匹配因素以及主腹杆规格数量较少的影响，随着主弦规格的增加，临界载荷和临界应力存在波动，整体呈增加趋势。由此说明设计臂架时应考虑主腹杆规格匹配的影响，以达到臂架稳定性最佳。

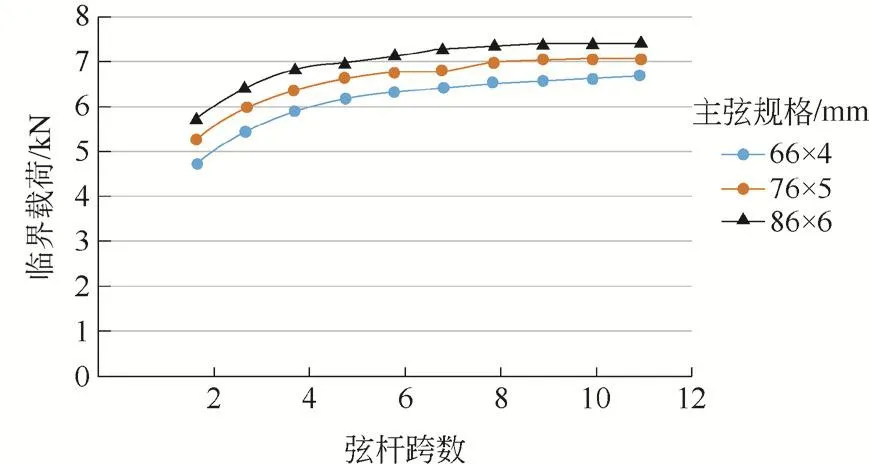
图9 屈曲临界载荷随弦杆跨数变化曲线

图10 屈曲临界载荷随弦杆规格变化曲线

臂架尺寸优化前后的性能参数见表4，可以看出在不降低结构屈曲承载能力的前提下，优化后臂架质量明显减轻，降重约13.5%。

表4 臂架优化前后参数对比

4 结论

通过有限元分析，得到了桁架式臂架的屈曲破坏载荷，确定了单节起重臂破坏形式。此外，桁架臂结构的最大承载能力和临界轴应力与初始缺陷呈非线性关系，初始缺陷系数越大，一阶屈曲破坏载荷和临界轴应力越小。通过试验对比可知，按照理论规范计算得到的屈曲破坏载荷偏小，试验破坏载荷比按照理论计算得到的最大承载能力高出38.8%，说明按照规范计算得到的破坏载荷误差大，低估了塔机臂架的实际承载能力。试验破坏载荷和有限元计算结果很相近，误差约2.3%，且破坏位置与有限元计算位置一致，说明有限元法计算得到的臂架极限载荷更接近实际，验证了有限元模型的正确性。最后，在有限元基础上，优化塔机臂架规格，避免了材料浪费，结构实现轻量化13.5%。