基于布尔莎模型两种坐标系转换的实现与应用

骆宗万,曹良中,余芳滨,张雨霏

(九江学院 旅游与地理学院,江西 九江 332005)

1 引言

随着我国与国外数据、技术交流愈来愈密切，国外的很多地理数据产品包括遥感影像产品、气象数据以及再分析数据正愈来愈多的被国内科技人员所采用，而国内的一些数据产品如气象站点观测数据、风云系列数据也正慢慢走出国门。因国外地理数据产品，尤其是欧美国家的数据产品坐标系多采用WGS-84坐标系统，而国内实际工作中所使用的坐标系统主要有1954北京坐标系、西安80坐标系、CGCS-2000坐标系等[1,2],其中尤以西安80坐标系的历史数据最多，因此研究如何实现WGS-84坐标系与西安80坐标系的坐标转换具有重要的现实意义[3]。

针对该问题，多位学者进行了研究。高宝华等借助三参数法对站点数据进行了坐标转换[4]，赵飞燕等对四参数坐标转换方法进行了介绍和应用[5]，姚朝龙等将六参数模型在平面坐标转换中进行了应用[6]，以上所述几种方法对于坐标转换来说具有使用简便的特点，但因考虑的转换因子更少，在精度上有所欠缺。陈宇等从坐标系原点向联测点重心位置平移的角度出发，提出了一种改进的布尔莎转换模型[7]，张秋昭等为提高转换参数精度，削弱方程的病态问题，提出了站心坐标转换改进模型[8]，这两种新的模型虽然精度有所提高，但因使用条件和情况的限制，整个求取转换参数，实现两种坐标系之间相互转换的过程对于使用者而言复杂程度更大，不具有普适性。

前人的研究主要集中在对各种坐标转换模型精度和简便性的单一考量上，然而对二者综合考量与实践应用方面的研究较少。本文基于python这门简单易学且不受开发平台局限的跨平台开源性语言[9～11]，以编程的方式实现了布尔莎七参数转换模型，其过程借助该代码完成了WGS-84坐标系统与西安80坐标系统转换参数的计算，并通过ArcGIS软件，将该参数在栅格数据类型中进行应用。最后通过4个站点数据验证，该转换系数的数据精度满足工程需要。

2 数据与方法

2.1 数据

WGS-84坐标系是一种地心坐标系，其坐标原点位于地球的质心[12]，西安80坐标系属于参心大地坐标系,它们之间的坐标转换，归根到底是不同的空间直角坐标系之间的换算[13]，是WGS84椭球体与IAG75椭球体的转换问题,两种椭球体的坐标参数如表1所示。

表1 WGS-84与西安 80坐标参数

本文选用位于新疆北部布尔津县8个同时具有西安80坐标系和WGS-84坐标系的坐标点。其中SJD2、SJE6、SJE10、SJE11四个站点用于计算坐标转换参数，另外SJD5、SJE13、SJE14、SJE16四个站点用于检核七参数的精度。其分布情况如图1所示，其坐标信息如表2所示。

图1 WGS-84坐标系坐标点分布

2.2 方法

布尔莎-沃尔夫模型，也称默特模型，因在模型使用过程中七个参数Tx、Ty、Tz、Wx、Wy、Wz、m的部分参数的求解情况，它可被分为七参数转换模型、六参数转换模型、四参数转换模型和三参数转换模型[7,14,15]。本文主要研究的就是用以实现WGS-84坐标系到西安80坐标系转换的布尔莎模型七参数法。两个不同空间直角坐标的转换模型如式(1)所示：

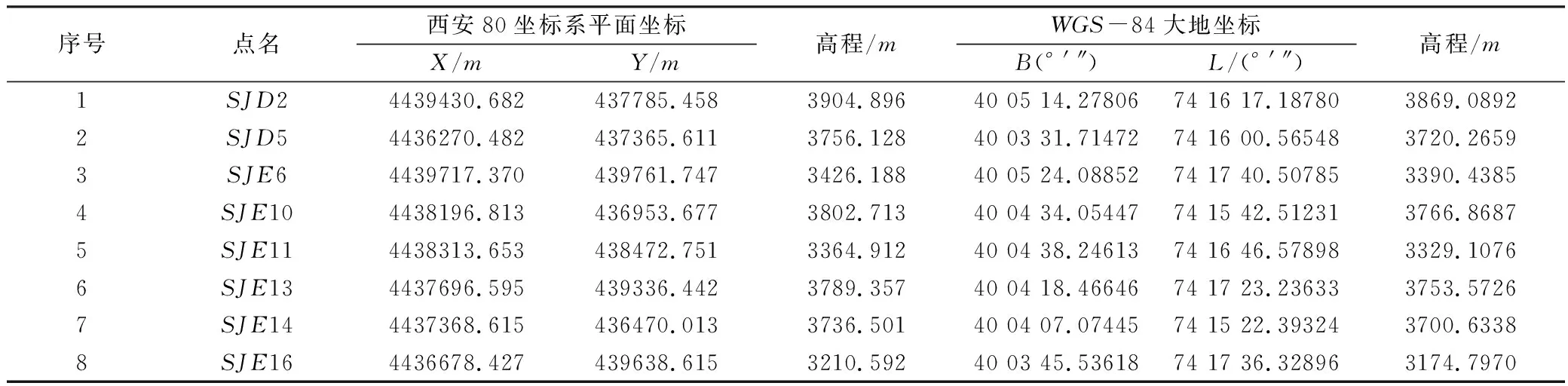
表2 站点坐标信息

(1)

式(1)中的(Xold,Yold,Zold)表示WGS-84坐标系成果，(Xnew,Ynew,Znew)表示西安80坐标系成果，三个平移参数Tx、Ty、Tz因两个坐标系的坐标原点不同产生，三个旋转角参数Wx、Wy、Wz因各坐标系相对应的坐标轴不平行产生，而尺度参数m则是因两个坐标系的尺度不一致所产生。式中共有Tx、Ty、Tz、Wx、Wy、Wz、m七个参数，被称为布尔莎七参数公式。当Wx、Wy、Wz均为小角度时，布尔莎七参数模型可以简化为式(2)：

(2)

列出误差方程式(3)：

(3)

为了检核坐标转换参数估计值的可靠性，本文采用外符合精度检测的方法得到外符合中误差m外，对参数估计值进行精度评定[16]。

(4)

其中△为误差，可由表2中的SJD5、SJE13、SJE14、SJE16四个站点数据和参数估计值代入误差方程(3)得到，n为测量个数。

借助于布尔莎模型进行参数求解及验证的流程如图2所示。

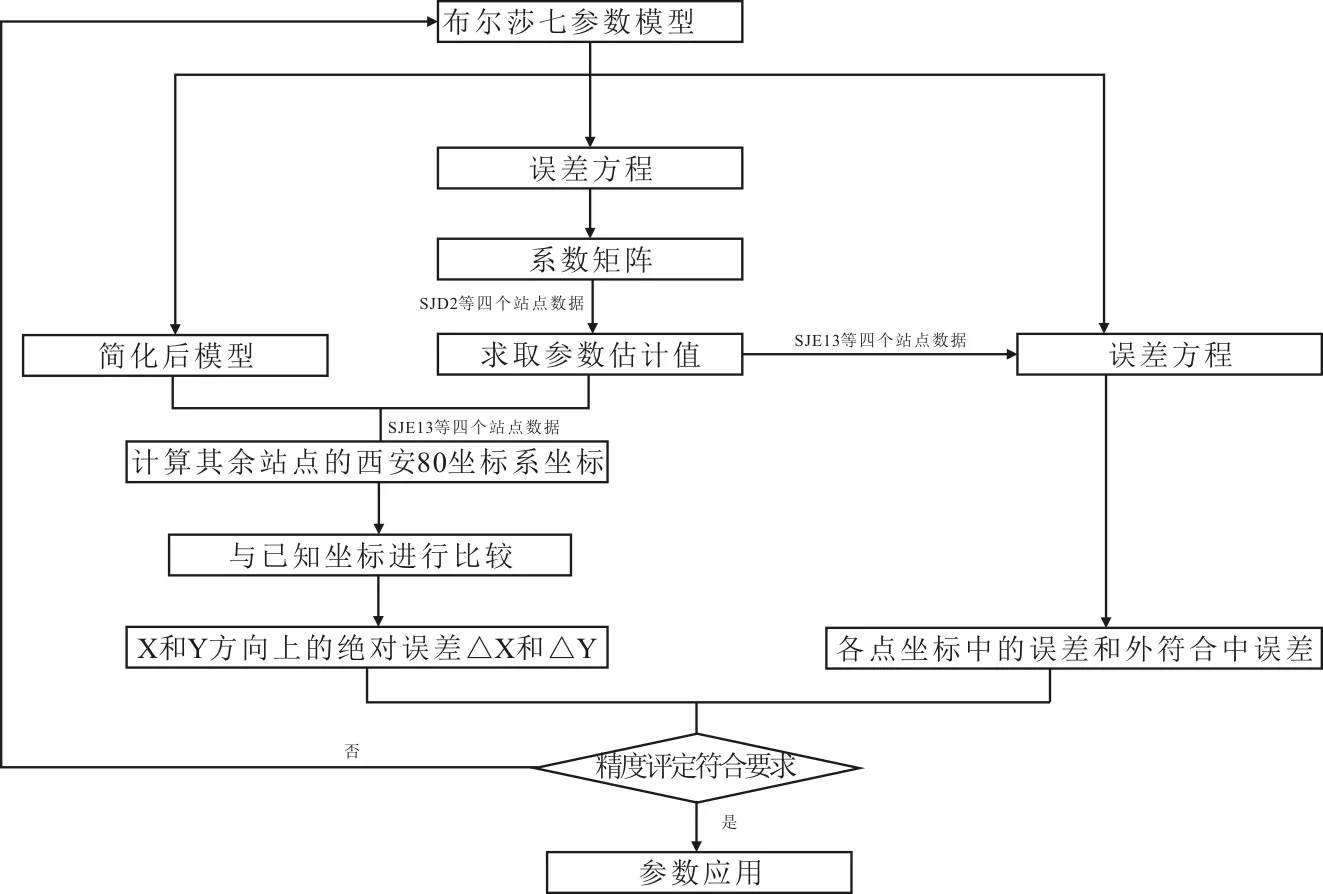
图2 工作流程

其中，用以求取参数估计值的部分代码如图3所示。

图3 具体实现部分代码

图3在求取参数值的过程中，首先将SJD2、SJE6、SJE10、SJE11四个站点数据代入系数列矩阵中，得到坐标转换的参数估计值，接着将坐标转换参数估计值和SJD5、SJE13、SJE14、SJE16四个站点数据代入误差方程中，得到用于计算外符合中误差做精度验证的各点中误差。这些过程与图2所示流程相一致。

在求取七参数并进行验证之后，通过ArcGIS软件实现WGS84坐标系下的栅格数据转换到Xian80坐标系下，其具体流程如图4所示。

图4 参数应用流程

图4中，首先，借助于ArcGIS中的自定义地理(坐标)变换工具，通过填入按照图2工作流程得到的参数估计值，建立起WGS-84坐标系与西安80坐标系坐标转换的转换参数；其次，使用ArcGIS中的栅格投影工具，将建立的转换参数写入，即可完成栅格数据由WGS-84坐标系到西安80坐标系的转换。

3 结果与讨论

使用图3中的代码，求解得到研究区内WGS-84坐标系到西安80坐标系的坐标转换参数，其值如表3所示。

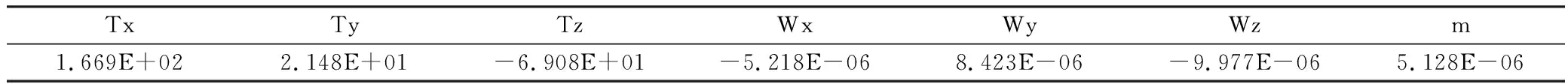
表3 坐标转换参数

表3中的参数估计值分别为X平移，Y平移，Z平移，X旋转，Y旋转，Z旋转，尺度变化m。

为了验证七参数的精度，选取SJD5、SJE13、SJE14、SJE16 站点计算出四个站点的计算坐标和已知坐标的差值ΔX和ΔY，对求解得到的七参数进行精度验证，其值如表4所示。结果表明：在X和在Y方向上的绝对误差ΔX和ΔY均小于0.05 m,通过将SJD5、SJE13、SJE14、SJE16站点数据代入方程式(4)得到的外符合中误差约为±0.071 m,精度满足工程测量的精度要求，可以进行参数应用。

表4 SJE13等4个站点数据转换成果

本文借助于ArcGIS软件，使用表3的参数，成功将图2中WGS-84坐标系下的栅格数据转换成为图5中西安80坐标系下的栅格数据。

图5 WGS-84坐标系坐标点分布

4 结论

本文采用布尔莎七参数模型实现了局部区域内WGS-84坐标系与西安80坐标系的转换，并将该参数在栅格数据上进行了实例应用，整个求取转换参数的过程不仅操作简便，而且坐标转换的结果经精度验证，误差较小，可以满足工程需求。