船舶航向自适应控制系统研究
2022-03-04齐迹李建民李伟
齐迹 李建民 李伟


摘 要:本文设计并模拟船舶航向自适应控制器,用于解决传统航向控制非线性系统在复杂环境下控制效果差的问题。控制器的系数可由Matlab LMI工具箱计算得出,针对航向控制非线性系统,采用自适应控制方法设计控制器,该方法可以保证船舶航向控制系统的全局有界性。最后针对实船验证,仿真结果表明该控制器性能良好,控制方法有效。
关键词:航向;自适应;控制系统;非线性;控制器
0 引 言
随着航行安全、节能、降低船员劳动强度等需要的提高,航向控制始终受到人们的高度重视[1-3]。但由于航速、外界干扰等条件的时变性,航向控制系统模型具有典型的不确定性及不稳定性,并且航向控制仅能量测航向角应用于反馈控制[4]。传统的控制器设计都是状态反馈控制(特别是针对线性系统),而针对非线性系统,特别是非线性项为不可量测状态的线性函数的非线性系统的状态观测器的研究较少[5-7]。本文利用航向控制非线性系统模型的特殊形式,基于Lyapunov设计了一种船舶航向自适应控制系统。
1 问题描述
设计船舶航向自动舵时,一般采用线性的野本方程建立船舶航向控制系统模型[8]。考虑非线性和外界干扰的影响,引入非线性项和外界干扰项,方程表达式为:
(1)
式中:为跟随线性指数;为航向角;为非线性指系数;为旋回性指数;为控制舵角。
取,则船舶航向非线性系统模型可转换为状态空间表达形式为:
(2)
船舶航向非线性控制系统的控制目的为在仅有系统输出可以量测的情况下,使系统输出即镇定到设定航向上。为此需要分析系统的结构与组成,设计航向自适应非线性控制系统的控制框架,其基本结构如图1所示。航向模型参考自适应控制结构如图2所示,相比较自适应调节器,模型参考自适应控制器稳定性更高,因此本文基于模型参考自适应控制器进行研究。
2 基于Lyapunov的船舶航向自适应控制系统
航向自适应控制系统以Lyapunov稳定性原理为依据,可以保证系统的渐进稳定性,而且可适用于系统参数大范围变化的情形[9]。系统假设如下:
①可调系统为线性时变系统,结构已知,参数可调;
②可调系统的状态变量均为可测。
设参考模型为:
(3)
可调系统模型为:
(4)
式中:为广义误差向量,可以得到关于e的微分方程为:
(5)
对任何初始条件xs(0)和分段连续的输入r(t),决定As(e,t)、Bs(e,t)的调整规律使得广义误差渐进趋于0,即
(6)
系统是全局渐进稳定的。且当t→+∞时,应有
(7)
以此基于Lyapunov稳定性理论构造自适应控制系统,构造下列二次型正定函数作为Lyapunov函数:
(8)
其中,,,。
进一步得到
(9)
上述自适应律可以保证自适应控制系统是全局渐进稳定的。
除了系统全局渐进稳定外,还要求可调系统参数收敛,即
(10)
由于As(e,t)、Bs(e,t)的调整仅仅依赖于广义误差e(t),故当自适应系统全局稳定时,有,而As(e,t)、Bs(e,t)趋于一个常数矩阵,即
(11)
可得
(12)
有三种情形可保证该式成立:①C≠0,D≠0,xs、r线性相关;②;③C=0, D=0, xs、r线性独立。
设系统的参考模型为:
(13)
(14)
广义误差向量为:
(15)
可以看到,需要调整的系数仅有和,取
(16)
根据,得到
(17)
(18)
则可取
(19)
最后得到系统参数:
(20)
(21)
3 仿真分析
仿真研究以“育鲲”远洋实习船为研究对象,该实习船的基本参数见表1。
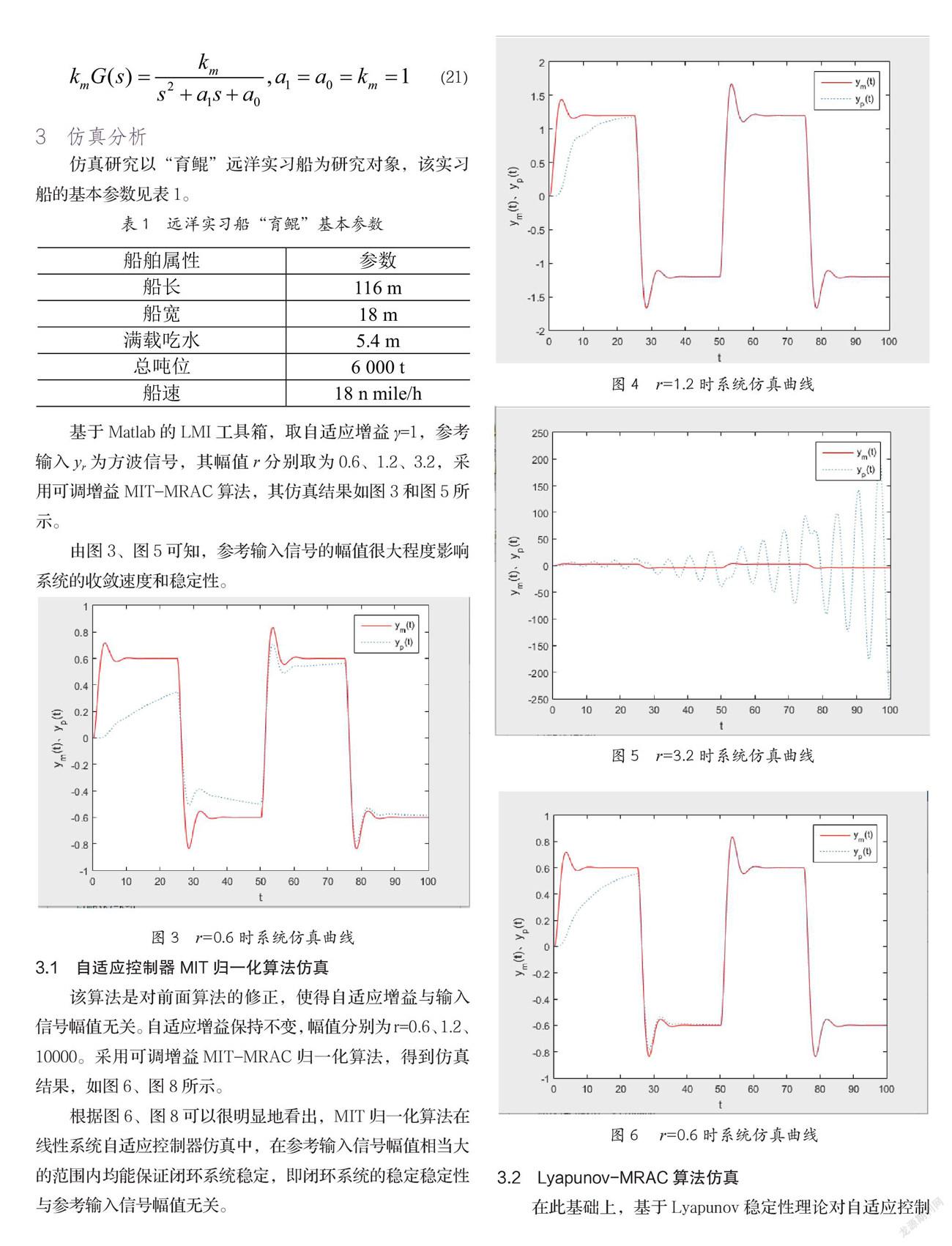
基于Matlab的LMI工具箱,取自适应增益γ=1,参考输入yr为方波信号,其幅值r分别取为0.6、1.2、3.2,采用可调增益MIT-MRAC算法,其仿真结果如图3和图5所示。
由图3、图5可知,参考输入信号的幅值很大程度影响系统的收敛速度和稳定性。
图3 r=0.6时系统仿真曲线
3.1 自适应控制器MIT归一化算法仿真
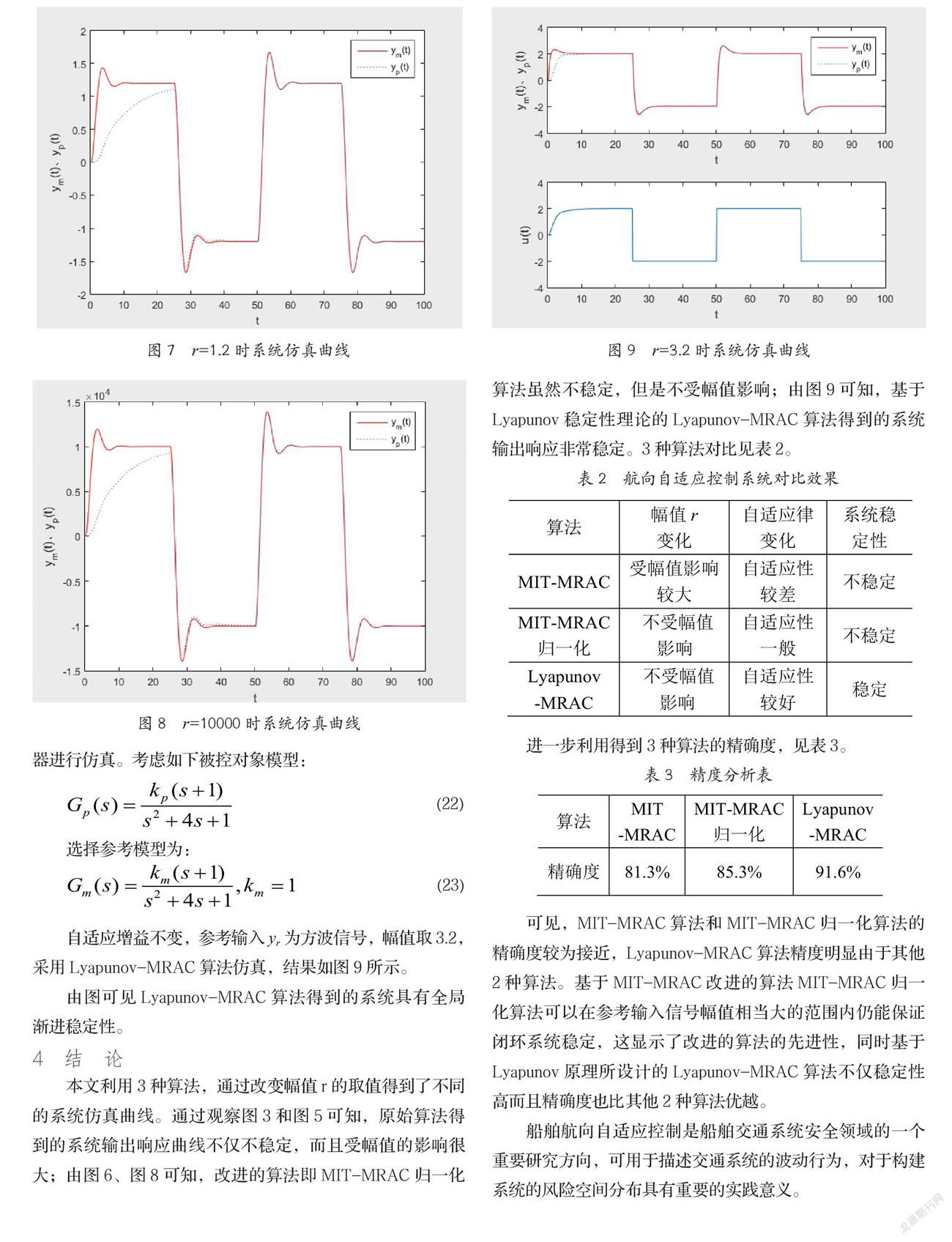
该算法是对前面算法的修正,使得自适应增益与输入信号幅值无关。自适应增益保持不变,幅值分别为r=0.6、1.2、10000。采用可调增益MIT-MRAC归一化算法,得到仿真结果,如图6、图8所示。
根据图6、图8可以很明显地看出,MIT归一化算法在线性系统自适应控制器仿真中,在参考输入信号幅值相当大的范围内均能保证闭环系统稳定,即闭环系统的稳定稳定性与参考输入信号幅值无关。
3.2 Lyapunov-MRAC算法仿真
在此基础上,基于Lyapunov稳定性理论对自适应控制器进行仿真。考虑如下被控对象模型:
(22)
選择参考模型为:
(23)
自适应增益不变,参考输入yr为方波信号,幅值取3.2,采用Lyapunov-MRAC算法仿真,结果如图9所示。
由图可见Lyapunov-MRAC算法得到的系统具有全局渐进稳定性。
4 结 论
本文利用3种算法,通过改变幅值r的取值得到了不同的系统仿真曲线。通过观察图3和图5可知,原始算法得到的系统输出响应曲线不仅不稳定,而且受幅值的影响很大;由图6、图8可知,改进的算法即MIT-MRAC归一化算法虽然不稳定,但是不受幅值影响;由图9可知,基于Lyapunov稳定性理论的Lyapunov-MRAC算法得到的系统输出响应非常稳定。3种算法对比见表2。
进一步利用得到3种算法的精确度,见表3。
可见,MIT-MRAC算法和MIT-MRAC归一化算法的精确度较为接近,Lyapunov-MRAC算法精度明显由于其他2种算法。基于MIT-MRAC改进的算法MIT-MRAC归一化算法可以在参考输入信号幅值相当大的范围内仍能保证闭环系统稳定,这显示了改进的算法的先进性,同时基于Lyapunov原理所设计的Lyapunov-MRAC算法不仅稳定性高而且精确度也比其他2种算法优越。
船舶航向自适应控制是船舶交通系统安全领域的一个重要研究方向,可用于描述交通系统的波动行为,对于构建系统的风险空间分布具有重要的实践意义。
参考文献
[1] 王雪峰.大型船舶横向非线性减摇自适应控制系统[J].舰船科学技术,2021,43(10A):7-9.
[2] 石浩.一种基于AIS数据的船舶航线自动规划方法[J].上海船舶运输科学研究所学报,2021, 44(1):25-30.
[3] 段俊利.基于历史航迹的船舶任意点到港的航线规划算法[J].上海船舶运输科学研究所学报, 2020, 43(2):10-15.
[4] 刘仁伟,薛彦卓.受限水域中船舶自动避碰模型及应用[J].哈尔滨工业大学学报,2018,50(03):171-177+184.
[5] Daejeong Kim, Soonseok Song, Tonio Sant, Yigit Kemal Demirel, Tahsin Tezdogan.Nonlinear URANS model for evaluating course keeping and turning capabilities of a vessel with propulsion system failure in wave[J]. International Journal of Naval Architecture and Ocean Engineering.2021,1-45.
[6] 王振雷,毛福兴,王昕.基于切换的多模型二阶段自适应控制器设计[J].控制与决策,2018,33(01):143-149.
[7] Dohwan Kim,Yuchang Won,Yongsoon Eun,Kyung-Joon Park.Resilient architecture for network and control co-design under wireless channel uncertainty in cyber-physical systems[J].Transactions on Emerging Telecommunications Technologies,2019,30(4):3490-3499.
[8] 文元桥.船舶行为的语义建模与表达[J].哈尔滨工业大学学报,2021,53(08):109-115.
[9] Aslam Muhammad Shamrooz,Dai Xisheng,Hou Jun.Reliable control design for composite-driven scheme based on delay networked T-S fuzzy system[J].International Journal of Robust&Nonlinear Control,2020,30(4):1622-1642.
基金项目:吉林省教育厅科学研究规划项目(JJKH20200333KJ,JJKH20200329KJ, JJKH20190909KJ,JJKH20190922KJ),国家自然科学基金项目(41671397),吉林省预算内基本建设资金计划项目(2020C037-7),吉林省科技发展计划项目(20191001008XH)
作者簡介:
齐迹,博士,硕士生导师,研究方向:信息工程及控制研究李建民,教授,船长,博士,硕士生导师,研究方向:交通信息工程及控制研究
