基于脉冲发动机特性的多弹协同制导律设计

潘辉 张振林 郭超

摘 要：针对攻击高速目标的多弹协同制导律设计问题，提出一种基于脉冲发动机工作特性的多弹协同制导律设计方法。 首先，求解视线系下的弹-目相对运动方程;其次，在视线方向上采用有限时间一致性理论进行协同制导律设计，视线法向采用滑模变结构控制理论进行视线角度约束制导律设计;然后，对于视线方向上过载指令，考虑脉冲发动机工作特性，将视线系下的连续制导指令转换为离散制导指令，进而实现多弹协同制导;最后，通过数值仿真验证了所设计协同制导律的可行性和有效性。

关键词：协同制导;一致性理论;角度约束;脉冲发动机特性;滑模变结构控制;离散制导;导弹

中图分类号：TJ765; V249.1 文献标识码：   A  文章编号：1673-5048（2022）01-0041-06[SQ0]

0 引  言

随着反导防御系统的不断增强，单枚导弹作战模式的弊端越来越明显。 应运而生的是多弹协同作战策略，该策略可以在现有导弹性能条件下，提高导弹的突防能力和毁伤能力，因此，很多学者致力于研究多弹协同控制算法。

为了实现协同攻击，国内外学者试图进行开环协作引导，即预先为所有的导弹产生一个共同的冲击时间，然后各导弹试图在时间上独立到达目标[1-4]。 Cho等[5]利用滑模变结构控制理论，保证各导弹的剩余时间趋于一致，而且为了防止制导指令的奇异性，给原有控制量附加分量。 文献[6]针对静止目标的固定时间协同攻击问题，设计了一种保证攻击时间和脱靶量的滑模面，实现了固定时间的协同攻击;针对匀速运动无机动目标，在原有制导律上利用预测拦截的概念，实现了匀速运动目标的协同攻击。 文献[7]采用简单的开环制导实现多导弹特定时间的协同攻击，但这只是将单导弹扩展到多导弹，在导弹攻击过程中没有弹间信息通信，不算真正意义上的协同。 针对上述问题，Zhao等[8]利用分布式算法进行协同制导律设计，每枚导弹都采用能量最优进行制导律设计，其后利用各枚导弹的剩余时间进行协同，也可以实现多弹协同。 文献[9]提出由两个阶段组成的协同制导方案。 在第一阶段，设计了一种特殊的分布式协商一致协议，使所有导弹都能渐近地达到状态一致性。 第二阶段采用局部视线控制律使导弹独立到达目标。 Song等[10]在攻击过程中考虑了通信噪声和通信拓扑切换，所有这些协同制导律都是在二维平面上提出的，并且假定导弹速度是恒定的。 Ryoo等[11]针对静止目标，提出以脱靶量和落角为约束的最优制导律，将该制导律转化为一个二次线性最优控制问题的解，仿真结果表明可以实现对时间和角度的控制。 文献[12-15]主要采用滑模控制、最优控制、Lyapunov稳定性定理、在传统比例制导律的基础上增加了一个攻击时间误差反馈偏置项等方法，设计多弹协同制导律，实现攻击时间和攻击角度的控制。 文献[16]在三维空间中采用快速非奇异终端滑模的控制方法在视线系下进行多弹协同制导律设计。 文献[17]提出采用弹目距离跟踪取代剩余时间跟踪的思想，仿真结果验证了该方法的确可以减小协同误差。

经过对现有文献的调查研究，多弹协同制导律设计多集中于静目标，针对动目标大多数采用有限时间一致性理论。 一致性理论均是要求速度可控，以此来实现多弹之间的协同。 但现有导弹在末制导段均不能达到这个要求。 因此，本文在现有理论的基础上，提出一种根据脉冲发动机特性进行设计的多弹协同制导律，该制导律真正能够采用脉冲式推力，实现多弹协同。

3 仿真分析

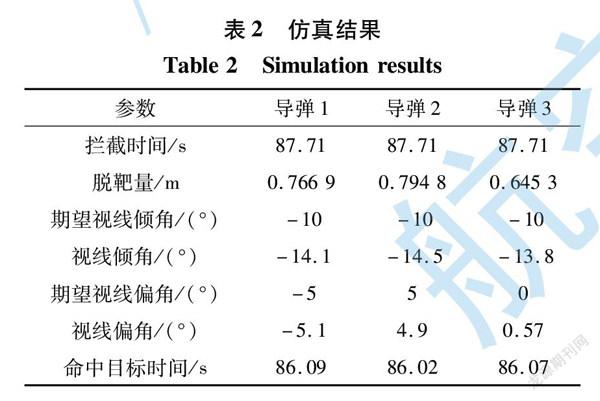
采用3枚导弹进行基于发动机特性的多弹协同制导律仿真，导弹和目标的初始信息如表1所示。 视线方向制导律的参数取值为：α1=0.9，α2=0.6，α3=0.33，n=3，通信矩阵E=011100100。 視线法向协同制导律的仿真参数为：ρ1=5，ρ2=1，γ=0.5，α1=α2=0.3，β1=β2=0.5，k1=0.06，k2=0.5，l1=0.6，l2=40， 仿真步长dt=0.01 s。 视线方向最大过载指令为10，视线法向最大过载指令为30，导弹的期望视线倾角和视线偏角分别为θcL1=-10°和ψcL1=-5°，θcL2=-10°和ψcL2=5°，θcL3=-10°和ψcL3=0°。 目标的机动能力：弹道系下俯仰通道过载为1，偏航通道过载为0。 结合式（9）、式（16）和式（21），即可得到多弹协同制导律的仿真如图3～13所示，误差信息如表2所示。

图3为导弹和目标的轨迹图，可以看出，在本文设计的基于发动机特性的协同制导律下，导弹的轨迹图较为平滑。 图4为导弹的速度曲线，导弹的速度变化范围最大为140 m/s，这在实际中是可以实现的。 图5为弹-目距离曲线，结合表2中的拦截时间，可以发现本文设计的协同制导律可以使导弹的协同时间误差较小。

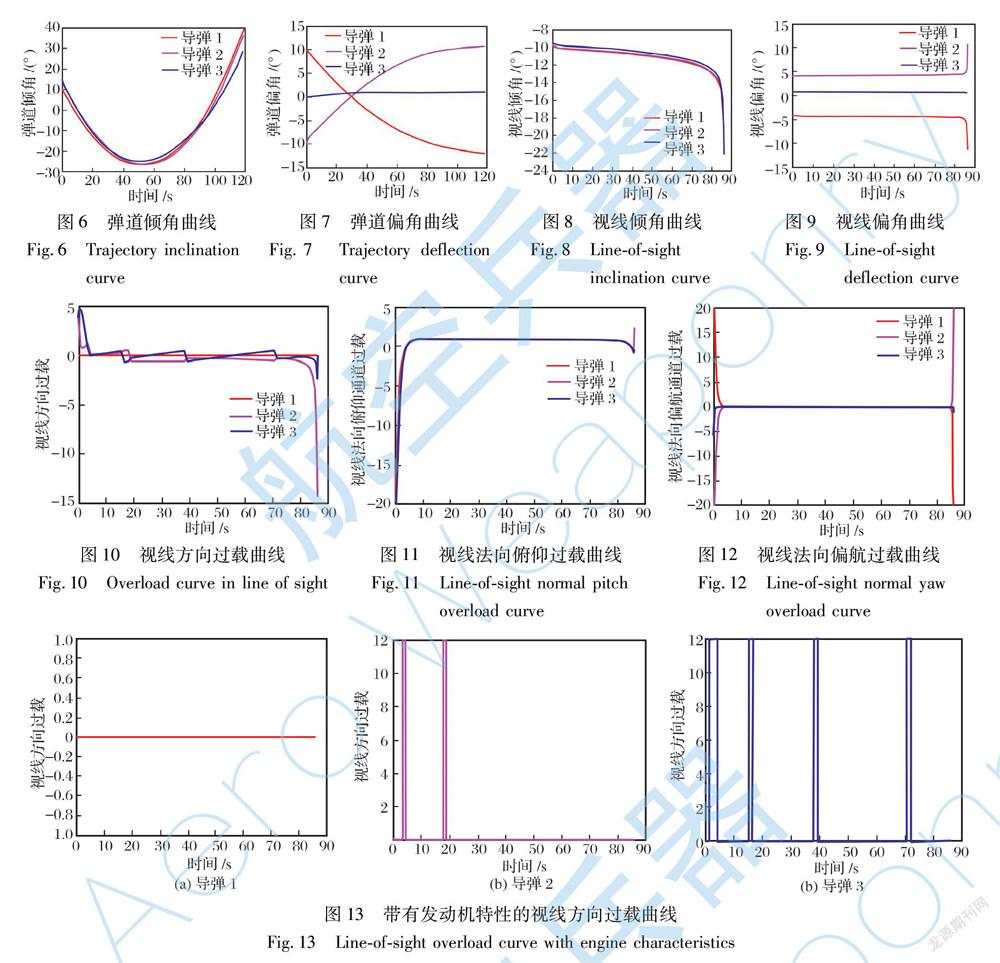
图6～9为导弹的弹道倾角、弹道偏角、视线倾角和视线偏角曲线，结合表2中的角度约束误差，最大误差为4.5°，误差较小。 并且表2中给出了导弹命中时间，可以发现，协同时间最大误差为0.07 s。 仿真结果表明，将连续的协同制导指令用脉冲发动机进行代替，可以获得非常高的协同打击精度。

图10～12为导弹在视线系下的过载曲线，可以看出视线方向上的曲线会出现一系列波动，这是采用脉冲发动机的输出作为导弹的输入过载导致的。 视线法向曲线在初始阶段进行调节，当满足角度约束后，曲线平滑。 图13为弹道坐标系下推力方向的过载曲线，这与2.3节的假设是吻合的，并且脉冲发动机能够做到这样的过载输出，在现实中易于实现。

4 总  结

针对高速目标多弹协同拦截问题，根据脉冲发动机的工作特性，设计了多弹协同拦截制导律。 现有协同制导算法要求导弹速度实时可控，但是，在目前条件下无法实现导弹速度的实时控制。 因此，针对该问题，提出采用脉冲发动机进行速度调节，以此实现多弹协同制导。 首先，根据视线系下的弹目视线相对运动模型，分别设计了导弹视线方向协同制导指令和视线法向制导指令。 其次， 根据发动机的工作特性，设计了发动机开关点火策略，将连续制导指令转化为离散制导指令，进而实现多弹协同制导。 最后，通过3枚导弹的协同仿真，验证了所提出的基于脉冲发动机特性的多弹协同制导律的可行性和有效性。

參考文献：

[1] Wang X F，  Zheng Y Y，  Lin H. Integrated Guidance and Control Law for Cooperative Attack of Multiple Missiles[J]. Aerospace Science and Technology，  2015，  42：  1-11.

[2] Zhang Y A，  Ma G X，  Liu A L. Guidance Law with Impact Time and Impact Angle Constraints[J]. Chinese Journal of Aeronautics，  2013，  26（4）：  960-966.

[3] Zhao Y，  Sheng Y Z，  Liu X D. Trajectory Reshaping Based Gui-dance with Impact Time and Angle Constraints[J]. Chinese Journal of Aeronautics，  2016，  29（4）：  984-994.

[4] 李友年，  江云，  李世华，  等. 基于有限时间控制方法的三维空间导弹制导律设计[J]. 航空兵器，  2016（3）：  26-29.

Li Younian，  Jiang Yun，  Li Shihua，  et al. Three-Dimensional Gui-dance Laws for Missile Based on Finite-Time Control Method[J]. Aero Weaponry，  2016（3）：  26-29.（in Chinese）

[5] Cho D，  Kim H J，  Tahk M J. Nonsingular Sliding Mode Guidance for Impact Time Control[J]. Journal of Guidance，  Control，  and Dynamics，  2016，  39（1）：  61-68.

[6] Kumar S R，  Ghose D. Sliding Mode Control Based Guidance Law with Impact Time Constraints[C]∥American Control Conference，  2013：  5760-5765.

[7] Zhao E J，  Wang S Y，  Chao T，  et al. Multiple Missiles Cooperative Guidance Based on Leader-Follower Strategy[C]∥IEEE Chinese Guidance，  Navigation and Control Conference，  2014：  1163-1167.

[8] Zhao J，  Zhou R. Distributed Three-Dimensional Cooperative Gui-dance via Receding Horizon Control[J]. Chinese Journal of Aeronautics，  2016，  29（4）：  972-983.

[9] Wang Y J，  Dong S，  Ou L L，  et al. Cooperative Control of Multi-Missile Systems[J]. IET Control Theory & Applications，  2015，  9（3）：  441-446.

[10] Song L，  Zhang Y A，  Huang D，  et al. Cooperative Simultaneous Attack of Multi-Missiles under Unreliable and Noisy Communication Network：  A Consensus Scheme of Impact Time [J]. Aerospace Science and Technology，  2015，  47：  31-41.

[11] Ryoo C K，  Cho H，  Tahk M J. Time-to-Go Weighted Optimal Guidance with Impact Angle Constraints[J]. IEEE Transactions on Control Systems Technology，  2006，  14（3）：  483-492.

[12] Zhao Y，  Sheng Y Z，  Liu X D. Analytical Impact Time and Angle Guidance via Time-Varying Sliding Mode Technique[J]. ISA Transactions，  2016，  62：  164-176.

[13] Jeon I S，  Lee J I，  Tahk M J. Impact-Time-Control Guidance Law for Anti-Ship Missiles[J]. IEEE Transactions on Control Systems Technology，  2006，  14（2）：  260-266.

[14] Saleem A，  Ratnoo A. Lyapunov-Based Guidance Law for Impact Time Control and Simultaneous Arrival[J]. Journal of Guidance，  Control，  and Dynamics，  2016，  39（1）：  164-173.

[15] Arita S，  Ueno S. Optimal Feedback Guidance for Nonlinear Missile Model with Impact Time and Angle Constraints[C]∥AIAA Guidance，  Navigation，  and Control （GNC） Conference，  2013.

[16] 郭正玉，  韩治国. 基于快速非奇异终端滑模的多弹协同制导律设计[J]. 航空兵器，  2020，  27（3）：  62-66.

Guo Zhengyu，  Han Zhiguo. Multi-Missile Cooperative Guidance Law Design Based on Fast Non-Singular Terminal Sliding Mode[J]. Aero Weaponry，  2020，  27（3）：  62-66.（in Chinese）

[17] 張振林，  张科，  郭正玉，  等. 一种新型领从式多弹协同制导律设计[J]. 航空兵器，  2020，  27（5）：  33-38.

Zhang Zhenlin，  Zhang Ke，  Guo Zhengyu，  et al. Design of a New Guidance Law for Guided Multiple Missiles[J]. Aero Weaponry，  2020，  27（5）：  33-38.（in Chinese）

[18] Wang X L，  Hong Y G. Finite-Time Consensus for Multi-Agent Networks with Second-Order Agent Dynamics[J]. IFAC Proceedings Volumes，  2008，  41（2）：  15185-15190.

[19] Ma G F，  Zhang H B，  Mei J. Distributed Finite-Time Attitude Regulation Control for Multiple Spacecraft Systems[C]∥31st Chinese Control Conference，  2012：  6439-6444.

Design of Multi-Missile Cooperative Guidance Law

Based on Pulse Engine Characteristics

Pan Hui1，Zhang Zhenlin2，Guo Chao1*

（1.China Airborne Missile Academy，Luoyang 471009，China;

2.School of Astronautics， Northwestern Polytechnical University，Xi’an 710072，China）

Abstract： Aiming at the design problem of multi-missile cooperative guidance law for attacking high-speed targets，  a design method of multi-missile cooperative guidance law based on the working characteristics of pulse engine is proposed. Firstly，  the relative motion equation of missile and target is solved. Secondly，  the finite-time consistency theory is used to design the cooperative guidance law in the line-of-sight direction，  and the sliding mode variable structure control theory is used to design the line-of-sight angle constrained guidance law in the line-of-sight normal direction. Then，  for the overload command in the line-of-sight direction，  considering the working characteristics of the pulse engine，  the continuous guidance command in the line-of-sight system is transformed into discrete guidance command，  and then the multi-missile cooperative guidance is realized. Finally，  the feasibility and effectiveness of the designed multi-missile cooperative guidance law are verified by numerical simulation.

Key words： cooperative guidance; consistency theory; angle constraint; impulse engine characteristics; sliding mode variable structure control;  discrete guidance;missile

收稿日期：2021-05-12

作者简介：潘辉（1982-），男，河南商丘人，硕士，高级工程师。

通讯作者：郭超（1988-），男，河南驻马店人，博士，高级工程师。