论高校公共体育课程隐性教育评价指标体系的构建

王永华 高继祥 王志鹏 王占坤

高校公共体育课程教育价值的生成具有依附性、隐蔽性、过程性、难量化性和评价描述的模糊性等特点。评价指标是教育价值的衡量方式，指标体系的构建以体育育人达成度为目标，采用代表性、系统性、方向性、独立性的基本原则，解构公共体育课程育人的隐性内涵。設置了三级衡量指标体系，逐层厘清公共体育教育价值的生成形式和呈现方式，用模糊数学模型的方式予以系统建构，形成模糊多级评价。

目前高校公共体育课程教学评价多采用定量的评价方式，以传统运动数据指标加以衡量，如速度、远度、成功率、命中率等指标，定量往往局限于一个狭小的空间维度，一定程度上限制了公共体育课程对学生综合素质形成的促进功能，抑制了体育教育促进大学生身心协调发展的本源价值。这一现象曾经受到国内专家、学者高度关注，相继催生了快乐体育、健康体育、文化体育、终身体育等体育理念。但是新教育理念实践的同时却没有与之相适应的衡量方式，传统显性评价方式无法支撑理念的落地生根。公共体育课程评价需要一套具有可操作性的评价体系予以规范和引导，以激发体育教育隐性育人价值的释放。体育课程隐性价值评价指标的开发是对传统体育课程的发展和完善，是以传统体育课程技术教学模式为载体，内嵌于体育显性课程中以间接、内隐方式呈现出来的体育教育要素总和。它具有隐蔽性、过程性、多样性、真实性、依附性、难以量化性、情境性等特征。体育课程隐性要素与显性价值紧密联系而又相互补充，各有侧重而又相互交叉，它与体育课程显性价值共同构筑了体育课程完整的体系，是“形式”与“内容”辩证统一关系，构建体育隐性课程评价体系不仅必要，而且迫切。

1 研究方法

文献资料法、逻辑分析法、访谈调查法。

2 体育课程隐性价值评价的数学模型

2.1 建立课程评价指标体系的基本原则

公共体育课程隐性价值评价体系是建立在快乐体育、健康体育、终身体育的基础上。评价指标的设置遵从了重要性、方向性、系统性和独立代表性原则。

2.1.1 重要性

不同维度下的评价内容繁多，在挖掘公共体育课程隐性教育价值的基础上，选择具有“生成性”价值的项目进行指标构建，确保评价指标本身的真实性。

2.1.2 方向性原则

评价指标设置要透过教学现象揭示公共体育教育本质，形式体现隐性教学内涵指标集合，集中反映高校公共体育教育理念、教学改革和发展的方向。

2.1.3 系统性

公共体育课程隐性评价是由教师、学生、课程内容等多种要素组成的相互关联的评价系统，评价指标不仅体现所属维度的教育内涵，还要兼顾多因素影响的情景教育效价。

2.1.4 独立代表性

被选取的评价指标应能独立反应公共体育课程隐性价值中某一方面关键信息。

2.2 确立公共体育课程生成性评价指标

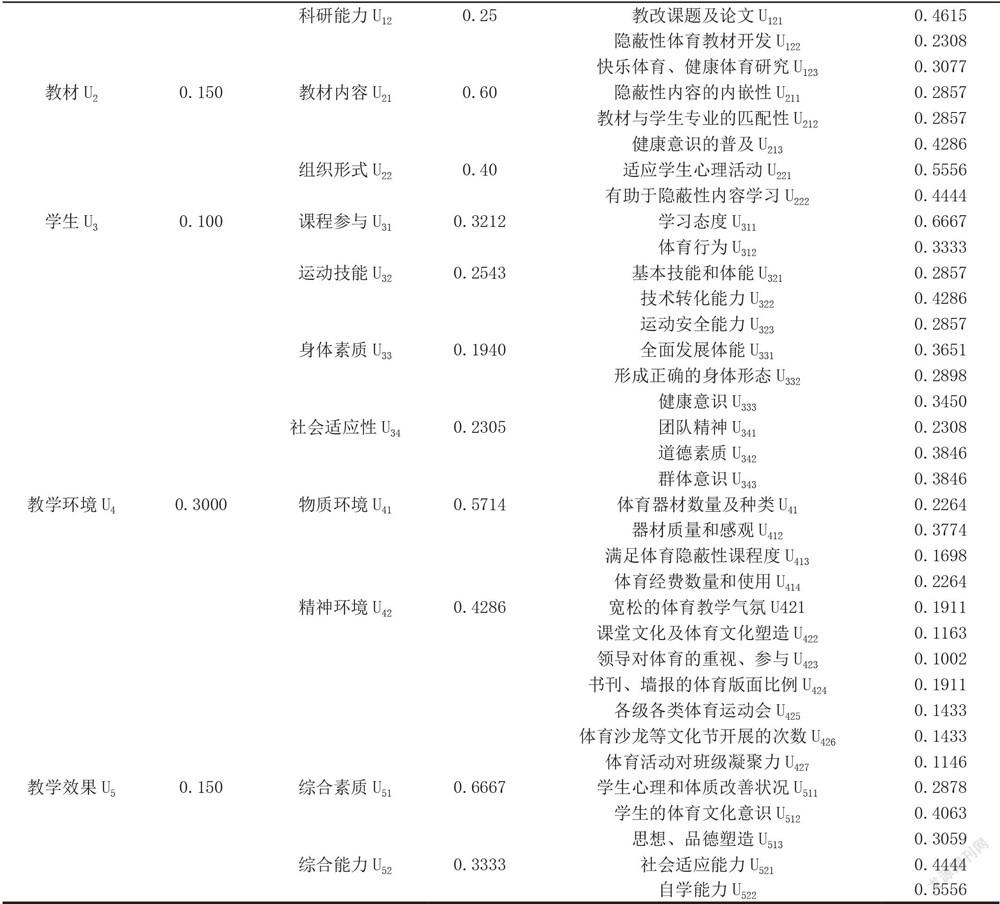
公共体育课程生成性评价体系获得，不是随意堆砌或简单罗列，而是建立在一个具体计量指标所赖以附着的基本框架上，即体育课程隐性要素是对学生教育价值效用的理论解释系统。体育隐性课程评价系统是经过反复调查和修正调整而确立的。设U是评价体育隐性课程教学质量的几个主要因素集合，其中包含5个一级指标，12个二级指标，43个三级指标（表1）。体育教师、学生、教材内容、教学环境是体育课程隐性效用能否最大化的核心资源禀赋。

2.3 建立公共体育课程隐性价值评价的数学模型

2.3.1 模糊数学评价

公共体育课程隐性价值评价是在不确定环境下进行的，考虑到多种因素对体育课程教学的影响，实现体育课程隐性价值的有效评价而做出的决策方法。

设两个论域：

U=（u1，u2，u3，……un）

V=（v1，v2，v3，……vm）

其中：U代表决定公共体育课程教学质量评价要素的多因素集合，（UK =体育教师、教材、学生、教学环境、教学效果）即为因素集;V代表多种评价结论构成的集合，即为评语集（V=非常好、较好、一般、较差、差）。由于各评价要素对体育课程隐性价值衡量存在不一致特征。所以，因素集中对公共体育课程隐性价值评价权重分配上存在一个模糊向量，记为X=（x1，x2，x3，……xk）∈ F（U）（xk表示因素集中的第K个因素的权重），满足       。因此，归纳后的评价视为V上的模糊集，记为Y=（y1，，y2，y3，……yL）∈ F（V），其中，yL示第L种评语在评语集中所占的位置。假设有一个U和V之间的模糊关系R=（rk L）n×m，通过R就可以获得模糊评价变换TR。由此，可以得出下面结构模糊评判数学模型。

因素集U=（u1，u2，u3，……un）

评价集V=（v1，v2，v3，……vm）

模糊变换TR=F（U）→F（V）

Y|→Y·R

上式关系中，R为U到V的模糊关系矩阵，R=（rkL）m×n，由（U，V，R）三个维度构成了一个模糊综合评判数学模型。假设输入因素集的一个权重值X=（x1，x2，x3……xk）∈ F（U），就能得到评价值Y=（y1，y2，y3，……yL）∈ F（V）。即为：

2.3.2 确定评价公共体育课程隐性价值评价的因素集

根据各指标内在联系，体育隐性课程评价体系共分5个一级因素级，即UKL，（其中：K=1，2，3，4，5，L=1，2，3，4）在UK中U1为体育教师因素，U2教材因素，U3学生因素，U4教学环境因素，U5教学效果因素。同理，有12个二级因素集，即UL（L=1，2，3，4）。构成一级因素为U =（U1，U2，U3，U4，U5），二级因素集和三级因素集的构成同理。

2.3.3 确定各评价因素权重

由于评价维度和评价指标的视角不同，其评价效用价值不同，即评价指标赋予的权重不同。评价权重在评价过程中能够表达出被评价对象轻重来，一组评价指标相对应的权重组成了权重系数，多组权重指标组成权重体系。使其能够客观体现被评价对象的教学效用。一组权重系數{WK|K=1，2，3……n}必须满足0<WK≤1和∑WK=1两个条件。

2.3.3.1 层次分析法

（1）确定体育课程隐性价值评价目标和评价因素。

（2）构造判断矩阵。矩阵元素的评价值反映了各元素对被评价对象重要性程度，通常采用1-7个要素证实其重要性的标度方法。判断矩阵元素的取值是在矩阵要素重要性比较中获得的具有客观意义的值，得到判断矩阵X=（xk l）n×m，当XkL =p时，XLK = 1/p。

表2矩阵标度及其含义一览表

（3）本研究采用方根法计算评价矩阵A的最大特征根极其对应的特征向量W，方法如下：

1）计算判断矩阵V每一行数值的乘积MK并计算其n次方根W=       =       计算向量W的权重数，即WK=        。

2）计算判断矩阵最大特征根  max=       。（XW）K表示向量XW的第K个元素，计算得到的特征向量就是评价指标所得到权重系数，代表评价指标的重要性程度。

（4）一致性检验

需要根据CI=（  max-n）/（n-1）和RI（评价随机性指标，查表得到） 来验证判断矩阵的一致性。随机一致性比率CI/RI<0.10时，证实层次分析法的结果具有一致性特征，也就是说评价指标的权重分配是合理的。否则，需要调整判断矩阵评价指标的取值，重新分配权重值。

表3层次分析法的平均随机一致性指标值一览表

2.3.3.2 计算评价指标权重

评价指标权重的计算依据前面所述的方法和程序，在层次分析法结构模型的基础上，按照一级因素集、二级因素集、三级因素集的顺序逐层计算各个指标的权重。首先计算教师U1，教材U2，学生U3，教学环境U4，教学效果U5，相对的重要性，构造评价矩阵如表4。

表4体育课程隐性价值一级评价矩阵

计算获得一级因素集权重分别为V=[0.3000，0.1500，0.1000，0.3000，0.1500]T，由此可以得到评价矩阵最大特征根

max=5.0060，对应特征向量w=（0.6189，0.3094，0.2063，0.6189，0.3094），CI=（  max-n）/（n-1）=0.0013<0.10（RI=0.00）。计算结果证明，一级判断矩阵具有满意的一致性，证实教师、教材、学生、教学环境、教学效果所占权重分别为0.3000，0.1500，0.1000，0.3000，0.1500。

二级评价包括五个要素集，相应构建五个评价矩阵，计算结果如下：

表5公共体育课程隐性价值二级评价矩阵维度1

计算获得此维度二级因素集权重为V=[0.75，0.25]T，最大特征根： max=2，对应特征向量（0.9487，0.3162）归一化后：w=（0.75，0.25）CI=（  max-n）/（n-1）=0<0.10（RI=0.00）。判断矩阵具有满意的一致性，教学能力和科研能力所占比重分别为0.75和0.25。

表6公共体育课程隐性价值二级评价矩阵 维度2

计算获得此维度二级因素集权重为V=[0.60，0.40]T，最大特征根：2，对应特征向量（0.8321，0.5547），归一化后：w=（0.60，0.40），CI=（  max-n）/（n-1）=0<0.10（RI=0.00）。判断矩阵具有满意的一致性，教材内容和组织形式所占比重分别为0.60和0.40。

表7公共体育课程隐性价值二级评价矩阵 维度3

计算获得此维度二级因素集权重为V=[0.3212，0.2543，0.1940，0.2305]T，最大特征根：4.2072，对应特征向量（0.6316，

0.5001，0.3814，0.4533），归一化后：w=（0.3212，0.2543，0.1940，0.2305），CI=（  max-n）/（n-1）=0.0767<0.10（RI=0.00）。判断矩阵具有满意的一致性。其中课程参与，运动技能，身体素质，社会适应性等指标所占评价比重分别为0.3212，0.2543，0.1940，0.2305。

表8公共体育课程隐性价值二级评价矩阵维度4

计算获得此维度二级因素集权重为V=[0.5714，0.4286]T，最大特征根：2，对应特征向量（0.80，0.60）健，归一化后：w=（0.5714，0.4286），CI=（   max - n）/（n-1）=0<0.10（RI=0.00）。判断矩阵具有满意的一致性，物质环境和精神环境评价比重分别为0.5714和0.4286。

表9公共体育课程隐性价值二级评价矩阵维度5

计算获得此维度二级因素集权重为V=[0.6667，0.3333]T，最大特征根：2，对应特征向量（0.8944，0.4472），归一化后：w =（0.6667，0.3333），CI=（   max -n）/（n-1）=0<0.10（RI=0.00）。判断矩阵具有满意的一致性，综合素质和综合能力评价比重分别为0.6667和0.3333。

三级因素集有十二个因素权重集，权重分配方式可以通过上述求解过程及检验方式获得，依次得出各单项评价指标的权重值，由于数量较多此处不再逐项罗列。（见表1）

2.3.5 模糊多级评价

具体操作如下：第一，按第三级因素UkLF单因素评价表在评语集V上建立相应的模糊子集YkLF=（ykLF1，ykLF2，ykLF3，ykLF4，ykLF5，ykLF6，ykLF7，ykLF8） 即表示这些因素集评价结果代表上一级的一个单因素评价结果。由此，得到单因素模糊评价矩阵RKL=（RkL1，RkL2，……，RkLF）T。第二，对UkL各因素进行三级综合评价，其权重向量WkL和RkL复合，结果为YkL=WkL·RkL =（ykL1，ykL2，ykL3，ykL4，ykL5） T ，可得到二级评价矩阵RK=（Yk1，Yk2，Yk3，Yk4，Yk5）T同理，其结果与权重向量集WK复合，进行二级因素集评价。第三，在二级因素集评价结果可得Yk=Wk·Rk=（yk1，yk2，yk3，yk4，yk5）T，构成一级因素评价矩阵Rk=（Y1，Y2，Y3，Y4，Y5）T评价结果与权重量集W复合，得到最终评价结果Y= W·R=（y1，y2，y3，y4，y5）。

2.3.6 体育课程隐性价值的评价

该研究的最终结果，需要计隶属度方法确定体育课程隐蔽性价值效度，取值k               时，即bk对应的评价结果，在评语集V中建立子集Q=（95，75，55，35），就可以对每个体育教师的体育课程进行评价，得分为C = P·QT 。

3 结论

依据公共体育课程生成性评价的特点和专家经验对体育课程生成性评价指标进行了构建，综合考虑了公共體育课程的隐性内容难以量化评价的特点，克服了以往评价指标的单一性和不全面性缺点。运用模糊数学和层次分析法计算各评价维度构成及指标权重，有效证实了公共体育课程结构要素与教学效果之间的因果关系，模糊数学的评价方法对高校公共体育课程隐性价值评价具有科学性和合理性，有效处理了评价体系中的定量和定性因素，具有系统性和可操作性。但是，评价指标的取舍对评价结论有较大影响，且公共体育课程改革是一个不断完善的过程，所以体育课程生成性评价指标体系的构建也需要不断探索和完善。

基金项目：浙江省哲学社会科学规划课题，名称：《体育锻炼预防青少年近视的去依附路径研究》编号：22NDJC102YB。

通讯作者：王占坤

（作者单位：1.温州医科大学体育科学部;2.宁波大学体育学院）