一种低轨卫星通信终端的数字波控方法*
2022-03-03
(广州海格通信集团股份有限公司,广州 510663)
0 引 言
使用低轨卫星星座进行宽带通信作为地面宽带通信的补充已经得到业内的普遍认可,两者相互结合可实现宽带通信无地域限制的覆盖。目前,低轨通信终端主要采用抛物面天线对星通信,使用该类天线的终端对星受限于其机械性而普遍精度及反应灵敏度不高[1-5]。针对这一问题,本文提出了一种基于相控阵的波控方法。该方法首先使用星历外推所得的卫星位置、地面终端安装的导航(如“北斗”)及惯导输出的位姿信息来计算终端对星指向角,并依此计算相控阵各阵元的移向量来完成低轨终端初始对星,然后通过数字圆锥扫描方法实现对星的持续跟踪。
1 相控阵的波控基本流程
相控阵天线通过控制其移相器的移相量来实现波束跟踪的阵列天线。低轨卫星终端首先利用接收到的卫星星历信息(两行根数或者是六根数的形式)推算卫星在任意时刻的位置(即卫星的经、纬度及卫星距地心的距离),再结合终端自身“北斗”所获取的终端经、纬度信息以及惯导的姿态输出即可获得终端与卫星的指向角。通过计算所得指向角即可得到相控阵各阵元移相器的移向量,从而实现终端初步对星。初步对星完成之后,利用数字域的圆锥扫描实现对星的精跟踪以弥补地球模型简单、星历和惯导输出误差等所带来的指向角误差。
2 地心坐标系、地理坐标系和载体坐标系
如图1所示,地心坐标系O-XYZ是在假设地球是一个规则球体的基础上定义的一个右手坐标系,其中X轴与首子午面和赤道面的交线重合,向东为正,Z轴指向北极,Y轴与平面O-XZ垂直,O点为地心。地心坐标系中的任意一点P可由其距坐标系原点O的距离s、射线OP在平面O-XY的投影与X轴的夹角α以及射线OP与平面O-XY的夹角β来表示,即
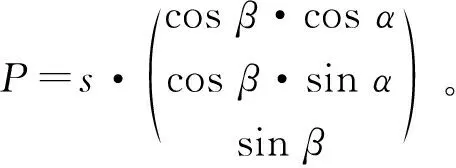
(1)
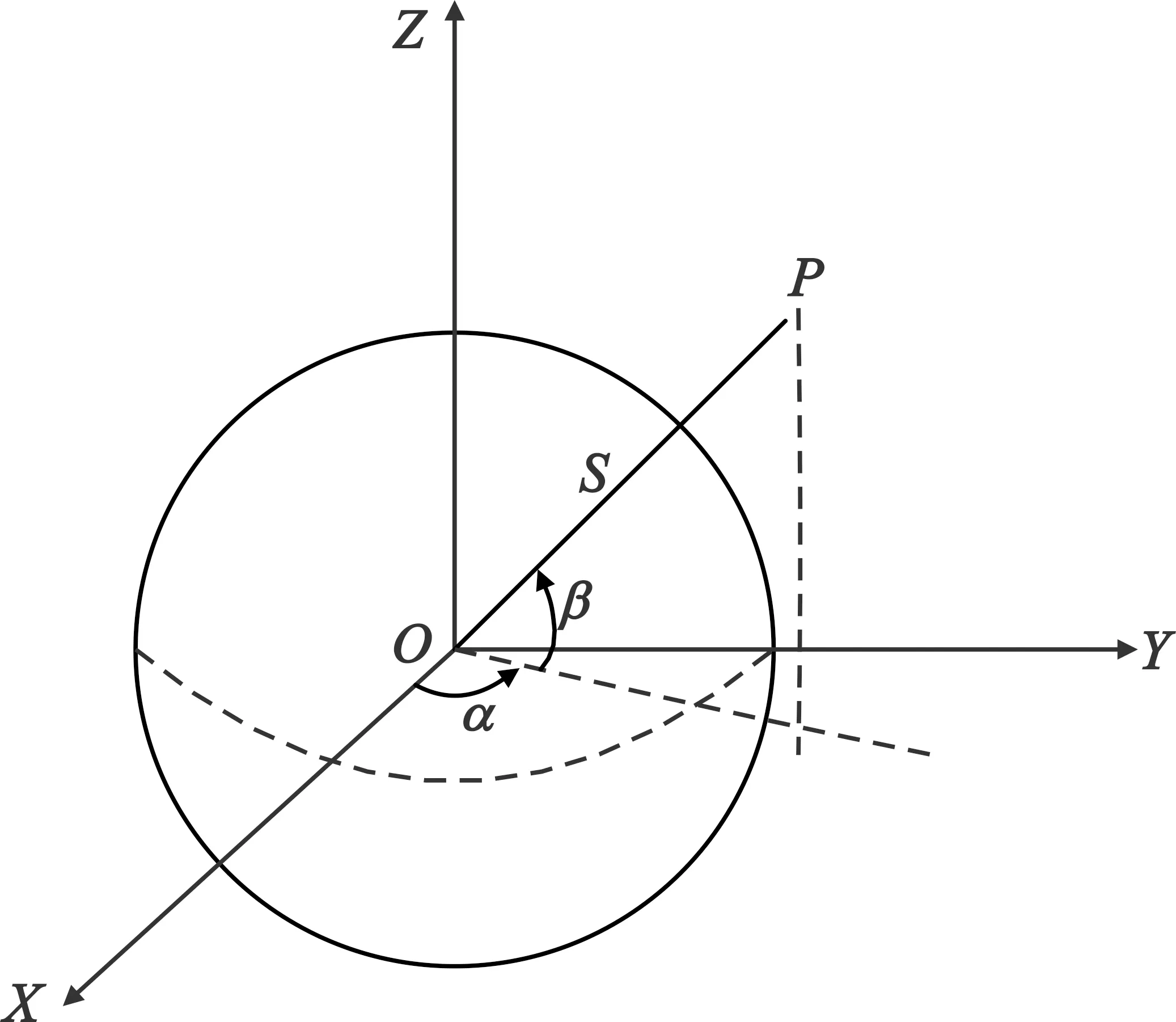
图1 地心坐标系示意图
如图2所示,地理坐标系OG-XGYGZG是以载体所在的地面点OG作为原点,其中OGZG指向正北,OGYG指向正东,OGXG与平面OG-YGZG垂直并指向地球外空。
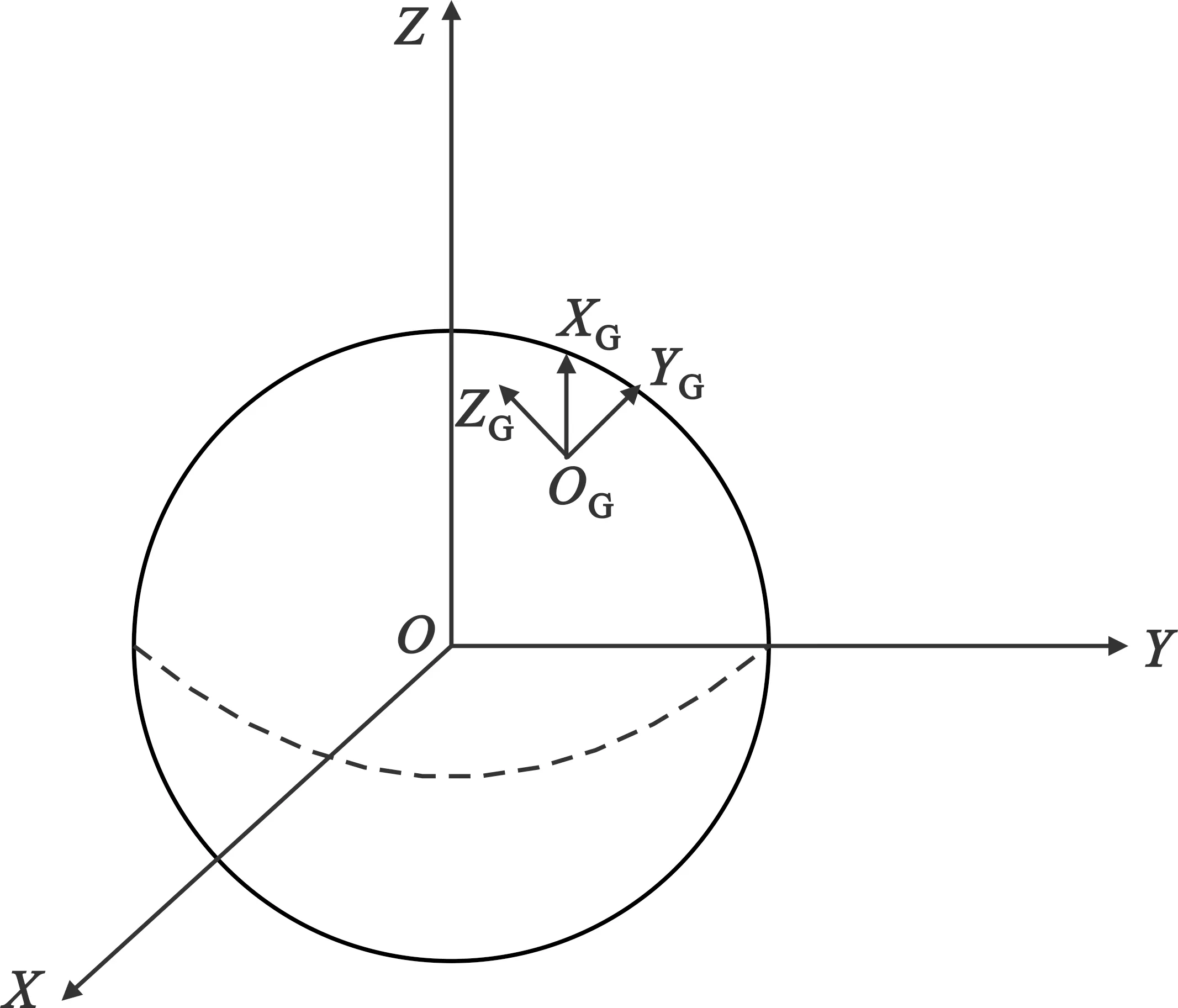
图2 地理坐标系示意图
如图3所示,载体坐标系OC-XCYCZC是以载体质心OC为原点,OCYC指向载体正前方,垂直于载体表面的轴为ZC轴,YC轴垂直于OC-XCZC,OC-XCYCZC是右手坐标系。在载体坐标系中绕XC轴逆时针旋转的角度称之为纵摇角,绕YC轴逆时针旋转的角度称之为横滚角,绕ZC轴顺时针旋转的角度称之为偏航角。
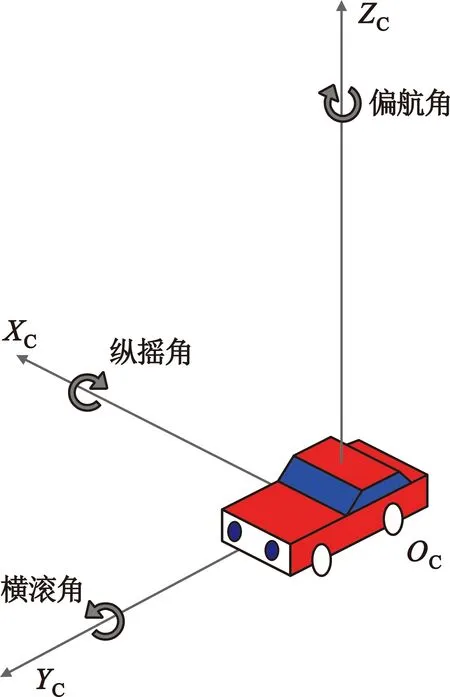
图3 载体坐标系示意图
3 数字波束跟踪
3.1 指向角计算
终端通过星历解算可以获取低轨卫星的实时位置信息。参考图1,假设t时刻低轨卫星星历解算的经、纬度结果为(α1,β1),且低轨卫星距离地心的距离为s,则由式(1)可知卫星在地心坐标系的坐标为
(2)
终端自身导航定位(如“北斗”)给出的经、纬度信息为(α2,β2),地球半径为r,则卫星在地理坐标系中的坐标为
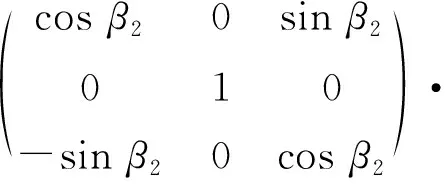
(3)
终端惯导所给出的终端姿态信息为(χ,ρ,κ)(这里χ表示航向角,ρ表示纵摇角,κ表示横滚角),则卫星在终端载体坐标系中的坐标为
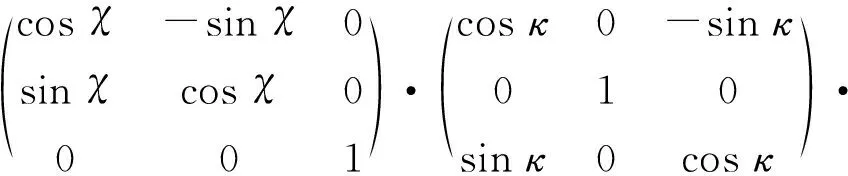
(4)
(5)
方位角为
(6)
3.2 相控阵移向量计算
如图4所示,假设相控阵(图中网格表示相控阵)位于载体坐标系的第一象限,图中射线表示波束方向,其在坐标系X-Y平面中的投影与X轴正方向的夹角为方位角,与X-Y平面中的夹角为俯仰角。
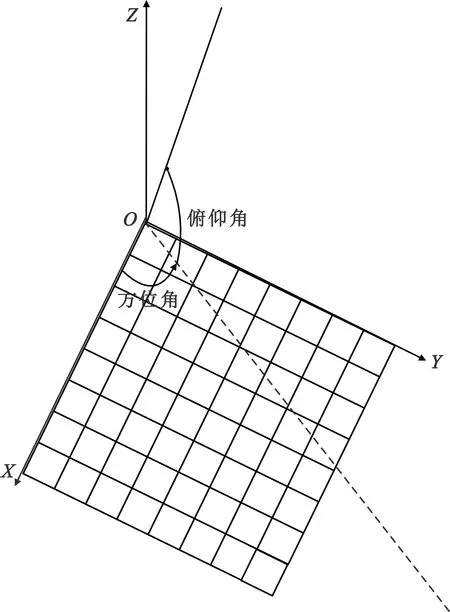
图4 相控阵天线于载体坐标系示意图
利用上一节所求得的俯仰角∠E和方位角∠A可以求得沿X和Y方向排列的直线阵列的均匀递变相位αx和αy:
αx=ξ×Δd×(cos(∠A)×cos(∠E)),
(7)
αy=ξ×Δd×(sin(∠A)×cos(∠E)) 。
(8)
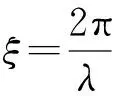
(9)
3.3 数字圆锥扫描
在完成上述波束指向后,可利用数字圆锥扫描实现对星的精跟踪,如图5所示。数字圆锥扫描过程刚开始时,相控阵天线指向与解算指向角方向重合。圆锥扫描首先通过控制移相器将相控阵天线指向偏离指向角一定角度,即圆锥扫描角度δ,然后以解算指向角方向做等轴旋转。
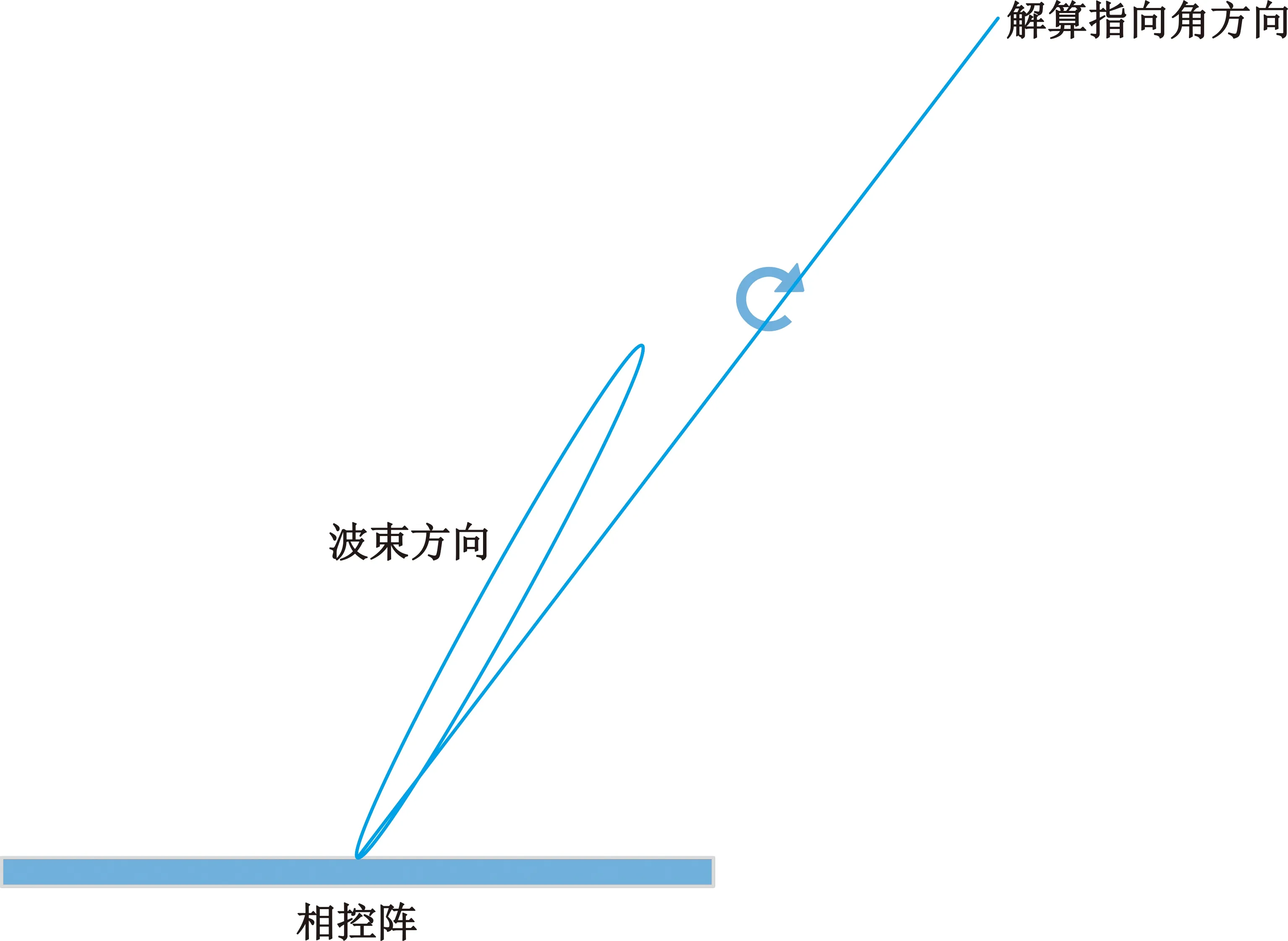
图5 数字圆锥扫描原理示意图
圆锥扫描的单次实现流程依据解算得到的方位角∠A和俯仰角∠E以及事先设定圆锥扫描角度δ推算得到单次圆锥上每个波束方向的方位角和俯仰角,其中单次圆锥每个点的方位角和俯仰角的计算公式[3]分别如式(10)和式(11)所示:
αi=∠A+sign(π-∠Oi)·
(10)
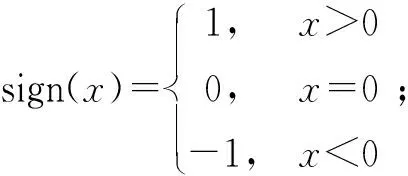
βi=arcsin(sin δ·cos∠Oi·cos∠E+cos δsin∠A)。
(11)
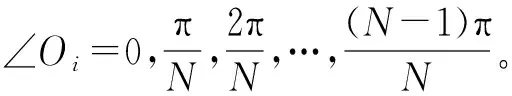
单次圆锥扫描后,记录圆锥扫描离散点的接收信号强度,记为P1,…,Pi,…,PN,N为单次圆锥扫描的离散点的个数。每次扫完一圈后计算信号强度P1,…,Pi,…,PN的方差:
(12)
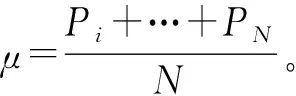
4 仿真验证
为了验证上述方法的正确性,本文进行了数值仿真。
4.1 指向角计算验证仿真
图6所示为测试场景。假设低轨卫星B与终端A具有相同经度,A点与B点的纬度差为x,此时卫星B在终端A所在载体坐标系的俯仰角图中所示θ。
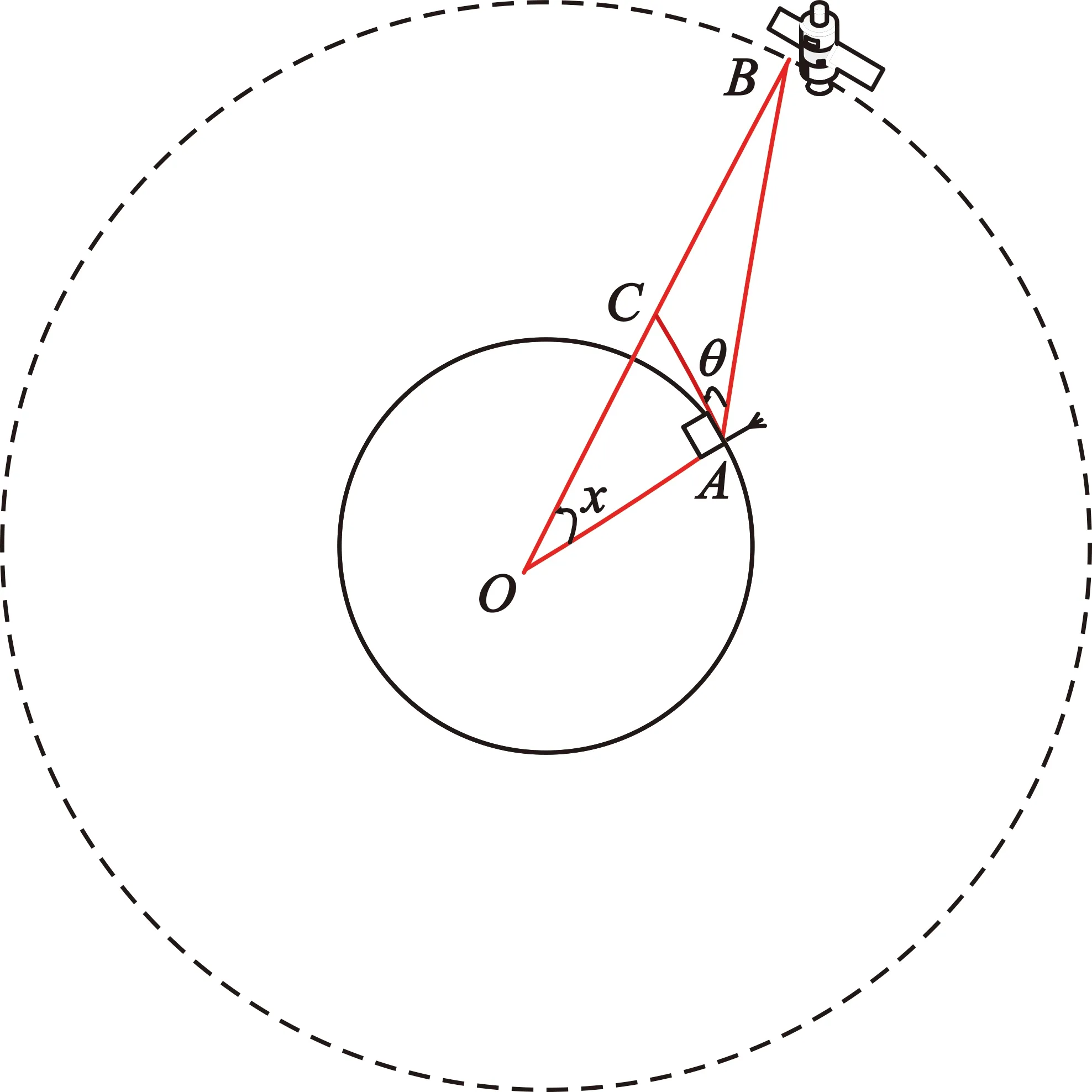
图6 卫星与天线几何关系图
在这种场景下,可通过三角关系求出卫星B在终端A所在载体坐标系的俯仰角θ。下面对该场景下俯仰角θ的理论值进行推导。
设OA为地球半径,OB为卫星与地心之间的距离,AB为卫星与终端之间的距离,C为地球所在圆过A点切线与OB之间的交点,由正弦定理可知,
(13)
另,
BC=OB-OC,
AC=OC·sinx。
(14)

(15)
即
(16)
针对上述场景进行了数值仿真,仿真中OA=6 378.137 km,OB=OA+1 000 km=7 378.137 km,相控阵的阵元为28×28,激励电流矩阵为
此外,低轨卫星与终端的经度均为东经30°,低轨卫星的纬度为北纬35°,天线阵的纬度为北纬30°,并假设惯导输出的航向角、纵摇角和横滚角均为0°。由式(3)可知AB=1 165.386 9 km,所以由式(17)可知,理论俯仰角为56.519 0°,按照3.1节和3.2节的计算流程并对各阵元激励电流添加3 dB范围内的随机增益,产生的方向图仿真效果如图7所示。
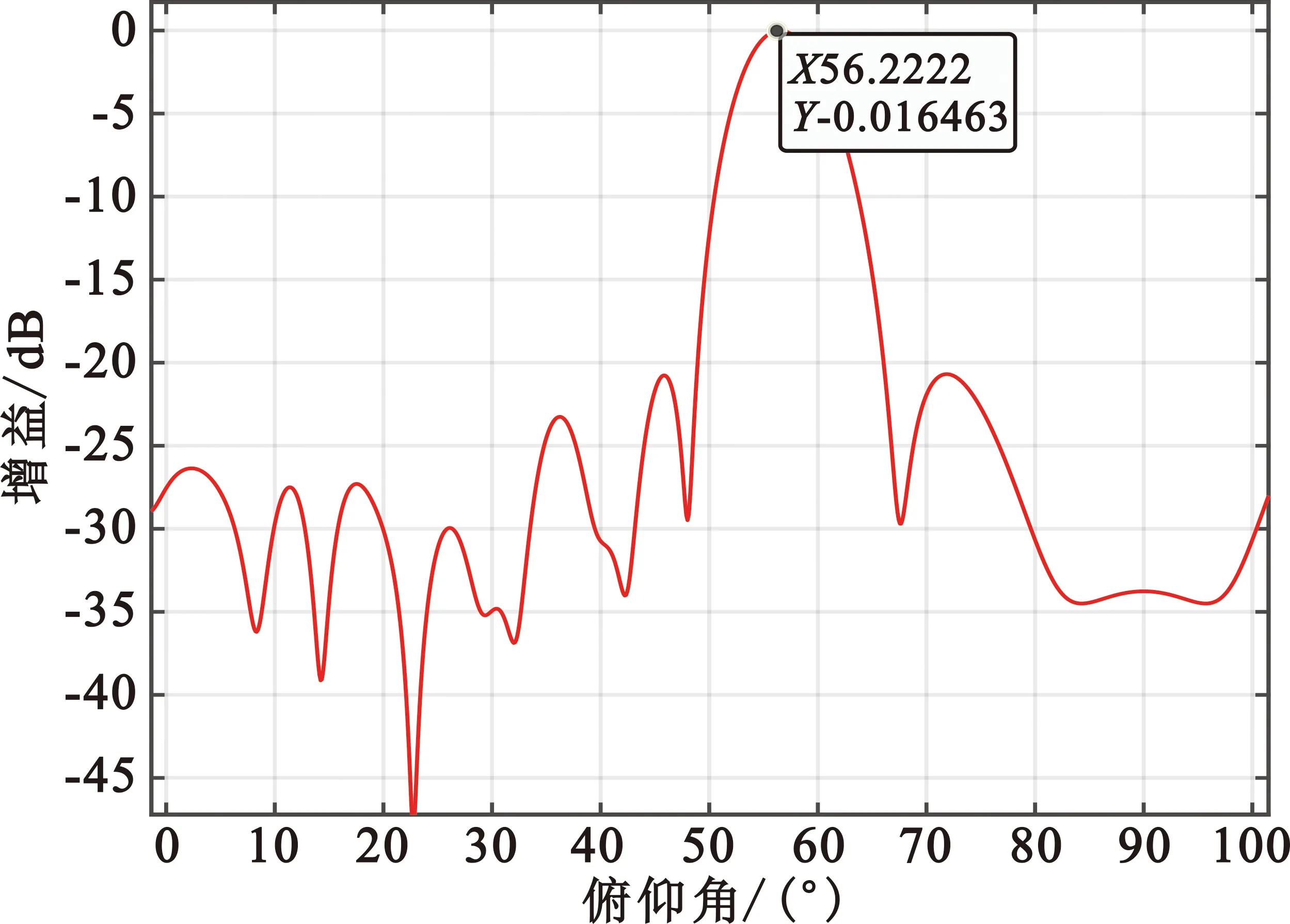
图7 相控阵指向角估计效果仿真图
由图7可知,在相控阵激励电流添加了随机误差后的俯仰角估计值为56.222 2°,与理论值是匹配的,证明了3.1节和3.2节计算流程的正确性。
4.2 数字圆锥扫描验证仿真
对单次数字圆锥扫描进行了模拟,模拟的阵列天线为4.1节中的28×28平面阵。假设阵列天线所在载体坐标系与其地理坐标系重合,根据3.3节的原理设置初始方位角α为0°,俯仰角β为45°,圆锥扫描角度为δ=2.5°,一周扫描的点的个数为180,仿真结果如图8所示,可见轨迹在空间呈现圆周状,且与X-Y平面呈现45°倾斜,说明了圆锥扫描的正确性。
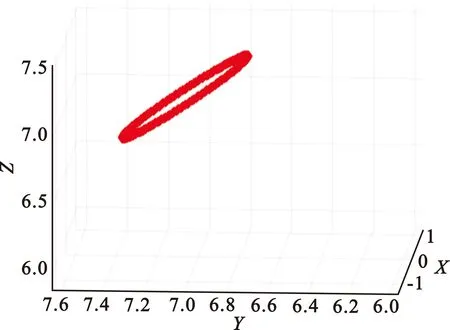
图8 数字圆锥扫描轨迹仿真图(100个扫描点)
对圆锥扫描跟踪仿真,如图9所示,第一次圆锥扫描的中心指向距离理论指向误差较大,经过再一次的跟踪之后,新的圆锥扫描中心指向与理论指向的偏差进一步缩小。
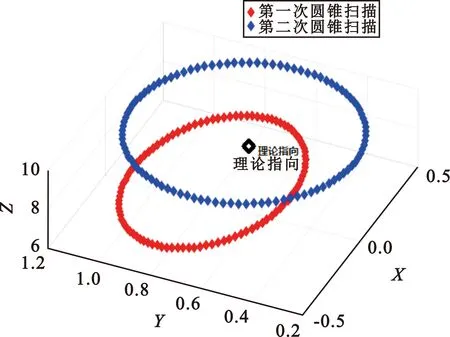
图9 两次扫描后的仿真效果
5 结束语
本文提出了一种低轨卫星通信场景下使用相控阵来实现对星的方法,避免了因使用抛物面天线而造成的机械误差所引发的固有追星不准的缺陷,具有良好的工程实现潜力。仿真结果表明所提波控方法追星效果较好。但为了达到更高的跟踪精度,波束的跟踪收敛算法可作为数字波控的进一步研究方向。
