基于需求侧响应的水风互补微电网容量优化配置
2022-03-03崔明勇杨林林杨少华
崔明勇, 杨林林, 杨少华, 张 涛
(燕山大学电气工程学院, 河北 秦皇岛 066004)
1 引言
微电网可实现可再生能源的集中发电,它将分布式电源、储能装置以及负荷集中在一起,构成了一个小型电力系统[1-3]。对微电网中电源容量配置进行研究是微电网规划设计的关键,对提高微电网经济性和可靠性具有重要作用[4,5]。
目前国内外已有不少关于含水电微电网的优化配置研究。文献[6]以风电-抽水蓄能电站为研究对象,提出了一种综合效益评价方法,对抽水蓄能电站的工作年限、配置容量等因素的变化对风电消纳容量和运行效益造成的影响进行了量化分析。文献[7,8]基于抽水蓄能电站、风电和光伏的互补效应,建立了以运行效益为优化目标的优化配置模型。文献[9]利用主成分分析法对风电-抽水蓄能电站联合运行系统中的抽水蓄能电站的容量进行优化。然而上述文献仅从发电侧出发,对以水电为主的多能互补发电微电网的优化配置进行研究,未考虑负荷侧的影响。随着可再生能源的大规模接入,其出力的不确定性对微电网的规划、调度带来的挑战也在不断增加。对于新能源渗透率较高的微电网而言,单纯从发电侧的角度出发已难以保证系统运行的经济性和可靠性。文献[10]对有无需求响应(Demand Response,DR)下微电网优化配置的结果进行了对比分析,结果表明计及DR可降低储能电池的配置容量,提高系统经济性。因此,有必要在微电网优化配置中考虑负荷侧的作用。
在计及了DR的微电网容量优化配置研究中,文献[11]在考虑DR下对储能投资商和用户进行了联合优化配置,但其采用的电价机制为固定分时电价机制,不能准确反映实际的供需情况。文献[12]以并网型光储微电网为研究对象,建立了基于DR的储能优化配置模型,但该研究的电价机制同样为固定分时电价且仅局限于光储型微电网,未拓展到含多种可再生能源互补发电的微电网。也有部分文献考虑了更加合理的动态分时电价策略:文献[13]基于可再生能源出力与负荷的相对大小将负荷划分为峰、谷两个时段,实现了动态分时电价机制,但其峰谷电价为既定值,未考虑峰谷电价对需求响应的影响,不能充分调动负荷参与DR的积极性。文献[14]以独立型风光柴储微电网为研究对象,采用隶属度函数将净负荷曲线划分为日峰谷时段,但该文献在DR模型中未考虑用户参与DR的满意度,不能充分保障用户利益,且在优化配置模型中未考虑能源互补性对优化配置结果的影响。
目前关于水电在微电网优化配置中的研究,大多集中于抽水蓄能,较少考虑径流式,但径流式小水电作为现有水电中的一种重要存在形式,对其在微电网中的应用进行研究,具有重要的工程实用意义。多种可再生能源互补发电可有效减少其出力的波动性,提高供电可靠性[15],因此需要重视能源互补性在优化配置中的作用。
同抽水蓄能电站相比,径流式存在调节能力不足的缺点,为此本文在其基础上增加了风力发电机、储能装置和柴油发电机,从而组成了并网型水风互补微电网系统,并在考虑水风互补效应的基础上,提出了一种互补度评价指标。在负荷端,基于短期水风出力与负荷需求之间的关系制定了一种动态分时电价机制,将负荷曲线划分为峰谷时段,实现了从固定分时电价向实时电价的转变;以负荷与水风互补发电差值累计和最小为优化目标,同时考虑用户参与电价引导的满意度,对动态分时电价中的峰谷电价进行寻优,并计算DR后的负荷。源端模型基于DR后的负荷和所提出的运行控制策略,以年运营收益和水风互补度为优化目标,通过源荷两端模型的交替迭代,对各分布式电源的容量配置进行优化。采用改进粒子群算法结合目标规划法对模型进行求解,通过对比不同方案的仿真结果,验证了所提方法的有效性。
2 微电网系统结构及微电源数学模型
2.1 微电网系统结构
本文所研究的并网型水风柴储微电网系统的拓扑结构如图1所示。

图1 微电网系统结构Fig.1 Micro-grid system structure
小水电、风电机组、储能装置、柴油发电机通过变换器接入交流母线组成了一个并网型水风互补发电系统。储能装置可以起到平衡功率与缓冲能量的作用,柴油发电机和配电网是系统中电量的补充和备用。微电网系统通过公共连接点(Point of Common Coupling,PCC)与配电网相连。
2.2 微电源数学模型
2.2.1 径流式小水电
相较于抽水蓄能电站,径流式由于受自然条件的影响无调节库容或可建库容较小,基本无调节能力,当其单独供电时,在丰水期可能有一部分弃水,而在枯水期可能供电不足,其表达式如下:
Phy(t)=9.81ηQtHtΔt
(1)
式中,Phy(t)为t时刻径流式水电的输出功率;η为水电效率;Qt、Ht分别为t时刻的水流量与水头高度;Δt为时间间隔,Δt=1 h。
2.2.2 风力发电机
风力发电机输出功率的大小主要取决于风速的大小,其输出功率可用如下分段函数表示:

(2)
(3)
式中,Pwt_s(t)、Pwt_N分别为t时刻单台风机的实际输出功率与额定功率;vci为切入风速;vr为额定风速;vco为切出风速;v(t)为塔架安装高度处的风速;h为塔架的高度;href为参考高度,取9 m;vref为参考高度处的风速;α为指数,取1/7。
2.2.3 柴油发电机
柴油发电机的出力与油耗量VF(t)有关,如下式所示:
VF(t)=aPde_s(t)+bPde_N
(4)
式中,Pde_s(t)、Pde_N分别为单台发电机在t时刻的输出功率与额定功率;a、b为燃料成本系数。
2.2.4 蓄电池
蓄电池作为储能装置,其剩余电量总是随着充放电过程而不断改变,剩余电量与充放电关系的表达式如下所示[16]:
(5)
式中,Ebat(t)为t时刻单台蓄电池的剩余电量,kW·h;Pbat_c(t)、Pbat_d(t)分别为t时刻单台蓄电池充电功率和放电功率,Pbat_c(t)符号为负,Pbat_d(t)符号为正;ηc为充电效率;ηd为放电效率。
采用荷电状态SOC(t)来表示蓄电池电量状态[17],关系式为:
SOC(t)=Ebat(t)/Ecn_N
(6)
式中,Ecn_N为单台蓄电池的额定容量。
长期过充或过放都会影响电池寿命,充电和放电时SOC(t)计算如下所示:
SOC(t)=SOC(t-1)-Pbat_d(t)Δt/(Ecn_Nηd)
(7)
SOC(t)=SOC(t-1)-Pbat_c(t)ηcΔt/Ecn_N
(8)
3 需求响应
3.1 动态分时电价机制
目前常用的负荷时段划分方法大多为根据负荷曲线的分布规律将其划分为固定的峰谷时段,但在微电网中可再生能源出力与负荷需求具有不确定性和波动性,固定的时段划分难以准确反映微电网内的供需情况,因此本文基于短期水风出力与负荷需求的相对大小制定了一种动态分时电价机制,对负荷曲线进行了动态时段划分。本文采取的动态分时电价机制分为峰谷两时段,当负荷需求高于可再生能源发电量时,该时段为峰时段,反之为谷时段,表达式如下所示[14]:
(9)
式中,p(t)为t时刻电价;pp、pv分别为峰、谷时段电价;Pwt(t)、Phy(t)分别为t时刻全部风机和水电的输出功率,其中Pwt(t)=NwtPwt_s(t),Nwt为风机台数;L(t)为t时刻DR前的负荷需求。
3.2 动态分时电价模型
本文采用替代弹性来定量表示电价变化对用户响应行为的影响,其在基于峰谷电价的DR中,用来表示峰谷电价的拉开比例与负荷峰谷电量转移比例的关系。相较于需求弹性,替代弹性在计算时所需统计的数据较少,只需峰谷时段用电量以及峰谷电价即可,其数学表达式如下:
(10)
式中,sei,j为替代弹性;Qi、Qj分别为i、j时刻的负荷需求量;Pi、Pj分别为i、j时刻的电价。
由替代弹性可得用户在峰时段负荷削减比例ΔLp和谷时段负荷增加比例ΔLv计算公式如下:
(11)

由式(11)可得DR后的负荷需求量为:
(12)
式中,LDR(t)为DR后的负荷需求量;Tp、Tv分别为峰、谷时段。
3.3 需求响应模型
用户在电价的刺激下,改变固有用电模式来参与系统调峰,不合理的电价设置可能会造成用户响应不足或响应过度,达不到改善负荷特性的目标,进而影响优化配置的结果,因此有必要对峰谷电价进行优化。
3.3.1 需求响应模型的目标函数
需求响应模型中的目标函数为DR后的负荷与可再生能源发电差值的累积和,表达式如下:

(13)
目标函数中的优化变量为高峰电价pp和低谷电价pv。
3.3.2 需求响应模型的约束条件
(1)用户满意度约束
只有充分考虑用户参与需求响应的满意度,才能保证用户在调整负荷以适应可再生能源出力的同时又不损害用户利益,使用户感到满意。通过引入用户用电满意度Ceus,t和购电满意度Ceps,t来共同表示用户参与需求响应的满意度。
(14)
(15)
Cus≥Cus,min
(16)
式中,Cus为用户满意度;Cus,min为用户满意度的下限,本文取0.8;qt、bt分别为进行DR前t时刻的负荷总量与电费总量;Δqt、Δbt分别为t时刻进行DR前后的负荷改变量与电费改变量。
(2)负荷的转移量约束
因为能够响应DR的负荷量是有限的,所以要限制每个时段负荷的转移量。
xs(t)≤Xs(t)
(17)
式中,xs(t)为t时段负荷参与DR的实际转移量;Xs(t)为t时段可转移负荷量的最大值。
(3)负荷总量约束
一个周期内负荷转入总量Qsin(t)和转出总量Qsout(t)相等。
(18)
(4)电价约束
因为本文将峰谷电价pp和pv也作为了优化变量,所以要对其加以限制。
pp≥pv
(19)
4 微电网容量优化配置模型
4.1 目标函数
4.1.1 系统收益
本文所研究的收益为系统运营的净收益,即系统运行收益减去系统设备初始投资成本和运行成本费用。系统运行收益包括向负荷供电收益、风电和水电的补贴收益以及系统上网售电收益。
(1)向负荷供电收益(用户购电费用)fin为:
(20)
(2)风电和水电的补贴收益为:
(21)
(22)
式中,fwt、fhy分别为风电和水电的补贴收益;Cwt、Chy分别为风电和水电的补贴电价,分别取为0.3 元/(kW·h)和0.4 元/(kW·h)。
(3)上网售电收益fin_v为:
(23)
式中,Pg(t)为t时刻与配电网交换功率,系统上网售电时Pg(t)符号为正,购电时符号为负。
4.1.2 系统成本
系统成本包括设备的初始投资成本、运行维护成本以及柴油发电机燃料成本和治污成本。
(1)设备初始投资成本
C1=NwtKwtPwt_N+NdeKdePde_N
(24)
C2=NbtKbtPbat_N+NbtfcnEcn_N
(25)
(26)
式中,C1为风电机组和柴油发电机的初始投资成本;C2为蓄电池的初始投资成本;Kwt、Kde、Kbt分别为风机、柴油发电机和蓄电池的单位功率成本,单位为元/kW;fcn为蓄电池的能量成本系数,单位为元/(kW·h);Nde、Nbt、Nwt分别为系统中柴油发电机、蓄电池、风机的台数;Pwt_N、Pde_N、Pbat_N分别为单台风机、柴油发电机、蓄电池的额定功率;Ecn_N为单台蓄电池的额定容量;CRF(l,r)为设备的资本回收系数,r为利率,l为设备可使用年限。
设备的等年值投资成本为:
Cann=(C1+C2)CRF(l,r)
(27)
(2)设备运行维护成本Com
(28)
Com=Com_wt+Com_bt+Com_de+Com_hy
(29)
式中,Com_wt、Com_bt、Com_de和Com_hy分别为风电机组、蓄电池、柴油发电机和水轮机的运行维护费用;mwt、mbt、mde、mhy分别为风机、蓄电池、柴油发电机和径流式小水电单位发电量的平均运行维护成本,元/(kW·h);Pwt_s(t)、Pde_s(t)分别为t时刻单台风机、柴油发电机的实际输出功率。
(3)燃料消耗成本
(30)
式中,Kf为燃料成本系数,元/(kW·h);Pde(t)=NdePde_s(t),Pde(t)为t时刻系统中所有柴油发电机的输出功率。
(4)治污成本,其中污染主要为柴油发电机发电时所排放的CO2、SO2和氮氧化物。
(31)
式中,Cenv为治污成本;Gj为第j种污染气体的排放惩罚系数,元/(kW·h);m为污染气体总类数。
综上,可以得到系统运营净收益数学模型为:
C=fin+fwt+fhy+fin_v-Cann-Com-CF-Cenv
(32)
4.1.3 水风互补度
考虑能源的互补效应,提出一种互补度评价指标γ来分析水、风互补性对容量优化配置产生的影响。利用水、风互补发电之后的出力波动与单一可再生能源发电系统出力波动之和的比值作为互补度评价指标,数学表达式为:
(33)
式中,Pav为互补系统的平均出力;Pwt_av为风电机组的平均出力;Phy_av为径流式小水电的平均出力;γ取值范围为0~1,其值越小,水、风互补性越好。
4.1.4 目标函数
根据经济性和互补度两类评价指标,建立了微电网优化配置目标函数模型,表达式为:
(34)
由式(20)~式(33)可知,C和γ都是Nwt、Nbt、Nde的函数。
为方便计算,令maxC=min(1/C)。目标规划法是先对两个单目标函数进行求解,分别求出其各自的最优解(1/C)*和γ*,为使两个目标都达到理想的最优值,采用平方和法将双目标优化问题转变为单目标优化问题,表达式如下:
(35)
式中,F为最终的优化配置模型的目标函数,当F取得最优值时,目标函数C和γ也已最大限度地接近各自的最优值。
4.2 约束条件
(1)功率平衡约束
(36)
式中,ΔP(t)为t时刻系统功率缺额;Pbat(t)为t时刻蓄电池充放电功率,其中蓄电池充电时Pbat(t)为负,放电时为正,Pbat(t)=NbtPbat_s(t),其中,Pbat_s(t)为t时刻单台蓄电池实际输出功率。
(2)系统设备台数限制
(37)
式中,Nwt_max、Nbt_max、Nde_max分别为风机、储能电池和柴油发电机因场地限制所能安装的最大台数。
(3)柴油发电机输出功率约束
0≤Pde(t)≤NdePde_N
(38)
(4)污染气体排放量约束
为减少柴油发电机发电时产生的污染气体对环境造成的影响,需要对其污染物的排放量加以限制。
(39)
式中,Wem为污染气体排放量;βj为第j种污染气体的排放系数,g/(kW·h);Wem,max为污染气体最大排放量。
(5)蓄电池运行约束
荷电状态约束:
SOCmin≤SOC(t)≤SOCmax
(40)
式中,SOCmin、SOCmax分别为储能蓄电池最小和最大容量;SOC(t)为t时刻蓄电池的荷电状态;
充放电功率约束:
(41)
式中,PmaxC和PmaxD分别为蓄电池额定最大充、放电功率,PmaxC符号为负,PmaxD符号为正;Ecn_N为单个蓄电池的额定容量;ηD和ηC分别为放电和充电的效率,均取0.86;ΔP(t)为t时刻系统功率缺额,蓄电池充电时,ΔP(t)<0,放电时ΔP(t)>0。
(6)系统与配电网交换功率约束
Pgmax_buy≤Pg(t)≤Pgmax_sell
(42)
式中,Pgmax_buy为系统最大购电功率,符号为负;Pgmax_sell为系统最大上网售电功率,符号为正;通常微电网与电网的交换功率不超过负荷的30%。
4.3 微电网优化配置指标
(1)可再生能源渗透率
可再生能源渗透率为微电网中新能源发电量占总发电量的比例。
(43)
式中,Rp为可再生能源渗透率;此处Pg(t)为t时刻微电网从电网购入的电量,符号为负。
(2)负荷贴近度
本文采用负荷贴近度来表示用户参与需求响应的积极性,具体表达式如下:
(44)
式中,dp为负荷贴近度,由式(44)可知,负荷贴近度越大,用户参与需求响应的积极性越高,需求响应的效果越好。
4.4 运行控制策略
在所研究的并网型水风柴储微电网系统中,风力发电和水力发电受环境的影响较大且具有不可调节性[18],蓄电池可以起到平衡功率与缓冲能量的作用,柴油发电机和配电网是系统中电量的补充和备用。要想提高微电网的经济性以及使其安全可靠地运行,关键是制定合理的运行控制策略。本文根据一年中季节对小水电出力的影响,将其划分为枯水期和丰、平水期。系统运行控制策略流程如图2所示。
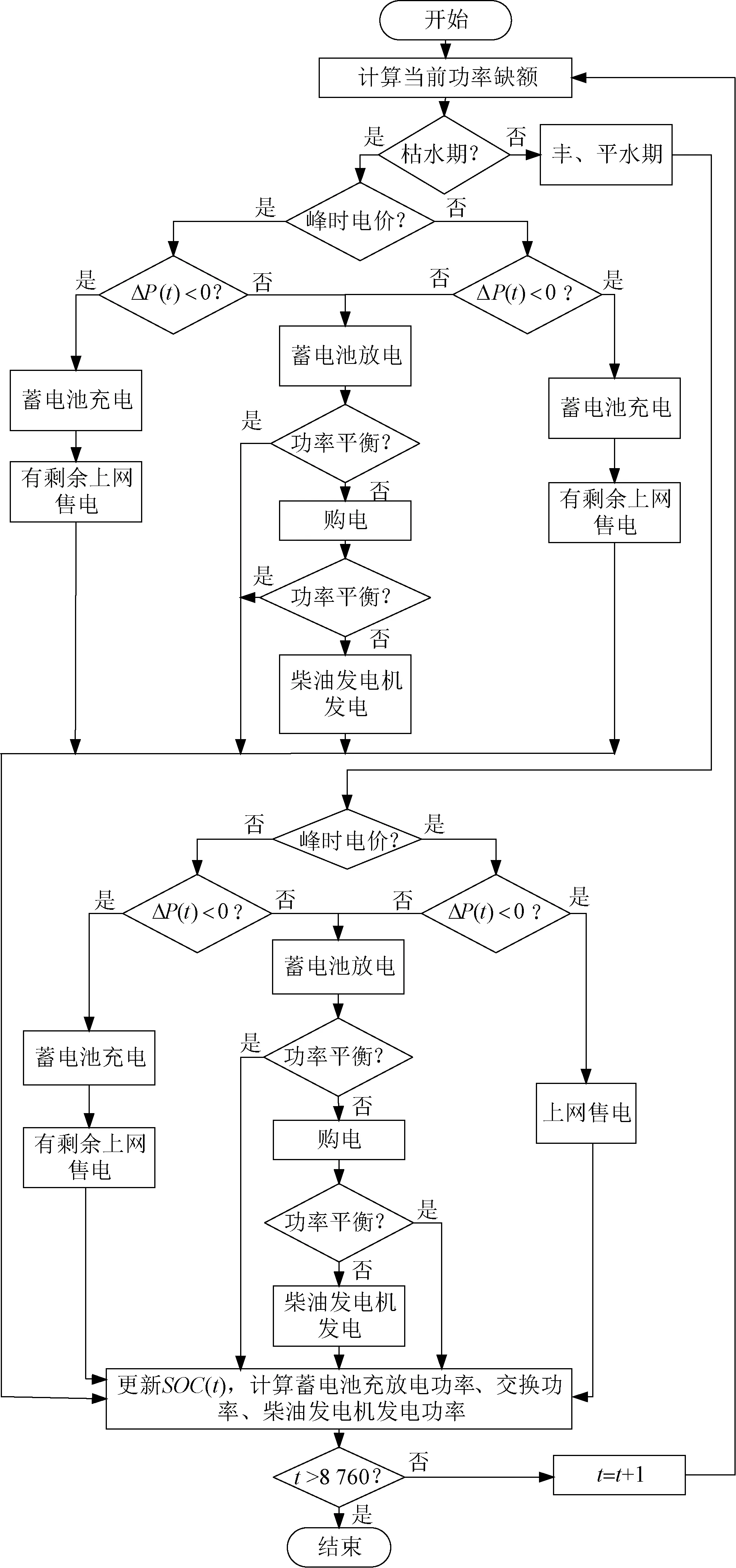
图2 运行控制策略Fig.2 Operational control strategy
首先使用风电和小水电为系统提供能量,并且时刻跟踪风电和小水电发电功率与负荷需求功率差额ΔP(t),当ΔP(t)>0时说明风电和小水电产生的电量不能满足负荷的需求,ΔP(t)<0时说明系统有多余的电量。
(1)丰、平水期内
在负荷高峰时段内ΔP(t)<0时,此时电价较高,而且小水电发电量充足,此阶段对蓄电池的依赖较小,可直接将系统多余的电量出售给电网,提高系统的收益;当ΔP(t)>0时,在蓄电池荷电状态和充放电功率允许的情况下,优先考虑利用蓄电池放电,若仍有缺额则由配电网和柴油发电机补充。在负荷低谷时段内ΔP(t)<0时,此时段电价较低,优先将多余的电量为蓄电池进行充电,为下一时刻的负荷高峰时段预留出调节容量,减少负荷高峰时段的功率缺额,若有剩余则出售给电网。
(2)枯水期内
枯水期内,小水电发电功率大幅降低,风电成为了系统内电量的主要来源。与丰、平水期不同,在枯水期负荷高峰时段内ΔP(t)<0时,优先给蓄电池充电,使其保持拥有足够的调节电量,若有剩余电量则上网出售。
蓄电池充电时,可通过式(41)来确定蓄电池的充电功率,若SOC(t-1)
5 模型求解方法
5.1 改进惯性权重的混沌粒子群算法
基于粒子群算法(Particle Swarm Optimization,PSO)的迭代公式如下[19]:
(45)
(46)
式中,Vi为粒子i的速度,Vi=vi1,vi2,…,vin;Xi为粒子i当前位置,Xi=xi1,xi2,…,xin;k为迭代次数;Psi、Psg分别为粒子i和整个种群目前搜索到的最优解;c1、c2为控制粒子向极值追踪速度的加速因子,本文取c1=c2=2;ω为惯性权重,可控制第k次迭代时的速度对第k+1次迭代时的速度产生的影响;r1、r2均为[0,1]之间的一个随机数。
惯性权重在粒子群算法中格外重要,能够协调算法全局搜索能力和局部搜索能力。采用Sigmoid函数S(t)来建立惯性权重ω的变化曲线,Sigmoid函数是具有S型生长曲线的非线性函数,对细微的变化非常敏感。引入群体适应度方差δ2来表示粒子收敛或离散的程度,其值越大粒子越分散,反之则越收敛,当|δ2|≤ε时,种群很有可能陷入了局部最优的情况,为避免这种情况的发生,可通过加入混沌变量λ来调节惯性权重值,以此来增加种群的多样性,如式(47)所示。
(47)
(48)
(49)
式中,Kmax为迭代次数的最大值;k为当前的迭代次数;ωmax、ωmin分别为惯性权重的最大和最小值,本文取ωmax=0.9,ωmin=0.4;ε为惯性权重的阈值,本文取ε=0.000 1。
群体适应度方差的表达式如下:
(50)

混沌扰动过程可用式(51)来表示,选用的是Logistic模型,通过λ对惯性权重ω的调节,可使ω的微小变化对后续搜索过程产生很大的影响,能够防止搜索过程陷入局部最优。
λi+1=4λi(1-λi)
(51)
式中,混沌变量λ的初始值取[0,1]之间的随机值。
5.2 计及DR参与的微电网优化配置模型求解
采用微电网优化配置模型与DR模型交替迭代的方式求出分布式电源的最优容量配置和最优峰谷电价,优化配置模型的求解流程如图3所示,其步骤如下:
(1)输入分布式电源的基本参数、水流量、水头高度、风速、负荷及初始电价等数据。
(2)初始化种群,优化变量为各分布式电源的台数以及峰谷电价。
(3)根据DR后的负荷,调用既定的运行控制策略,对优化配置模型进行求解,即在求解优化配置模型时,对各分布式电源的出力按既定策略进行调度。

图3 优化配置模型的求解流程Fig.3 Optimal configuration model solving process
(4)利用本次优化配置的结果,对需求响应模型进行求解,得到最优峰谷电价。
(5)将步骤(4)得到的峰谷电价代入优化配置模型中,重复步骤(3)~步骤(5),直至达到最大迭代次数,输出优化配置结果。
6 算例仿真与分析
6.1 基本数据
以某地区小水电供电区为研究对象,微电网系统与配电网通过10 kV交流母线相连。在Matlab中基于该地区一年的气象数据和负荷数据进行并网型水风柴储微电网运行和优化配置算例的分析,仿真时长为8 760 h,仿真步长为1 h。设蓄电池初始荷电状态SOC(0)=0.5,SOCmax取0.85,SOCmin取0.2;径流式小水电的装机容量为3 000 kW,年最大径流量为201 m3/h,由小水电全年水流量可知,1月~5月和12月为枯水期,6月~11月为丰、平期,全年水流量曲线如图4所示;全年风速曲线如图5所示,该地年平均风速为7.09 m/s,由全年风速曲线可知该地区春冬季节风速较大,夏秋季节风速较小;全年负荷功率需求曲线如图6所示,由图6可知该地区一年中夏季用电量最大。由全年风速和水流量曲线可知风电和水电在时间上具有互补性。
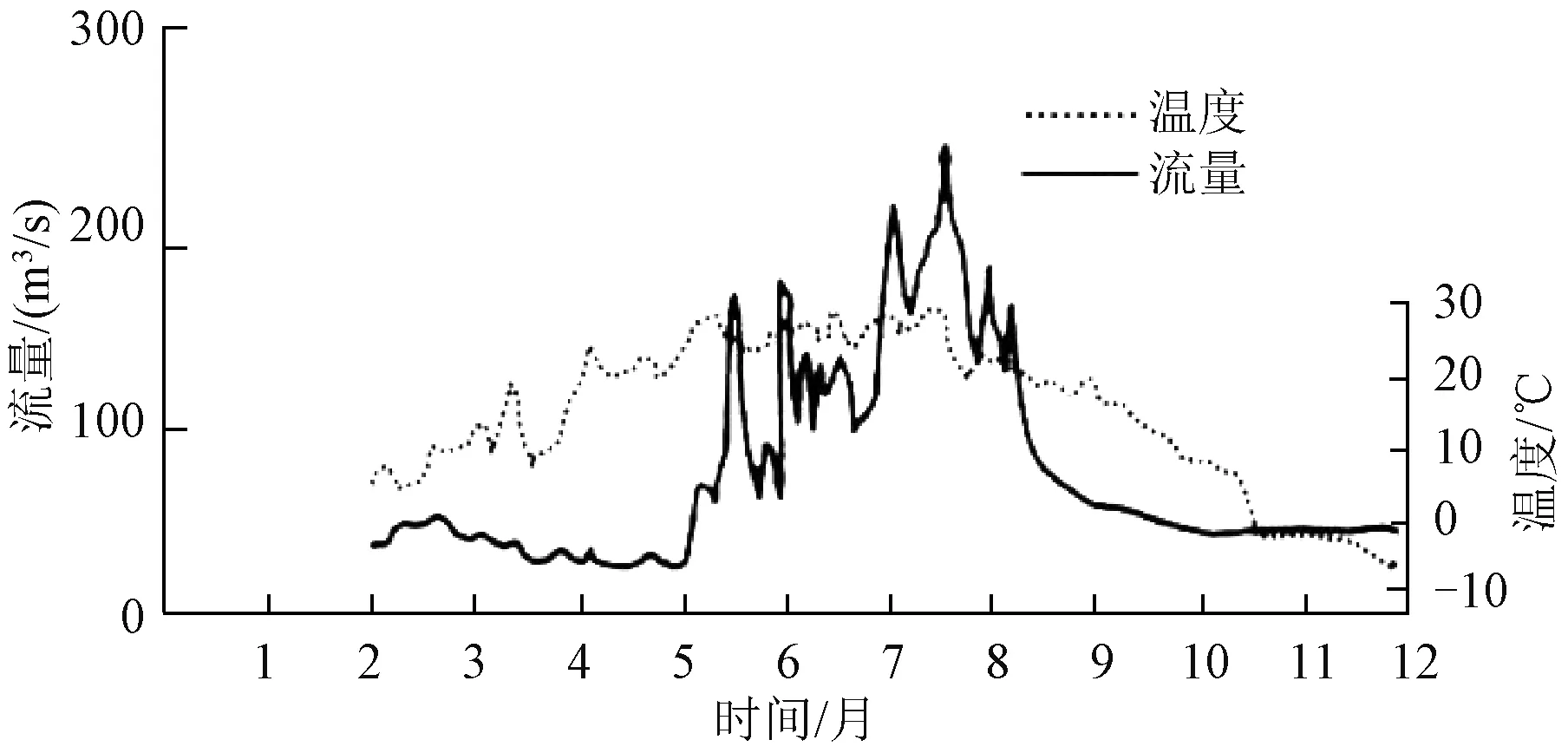
图4 全年水流量曲线Fig.4 Annual water flow curve
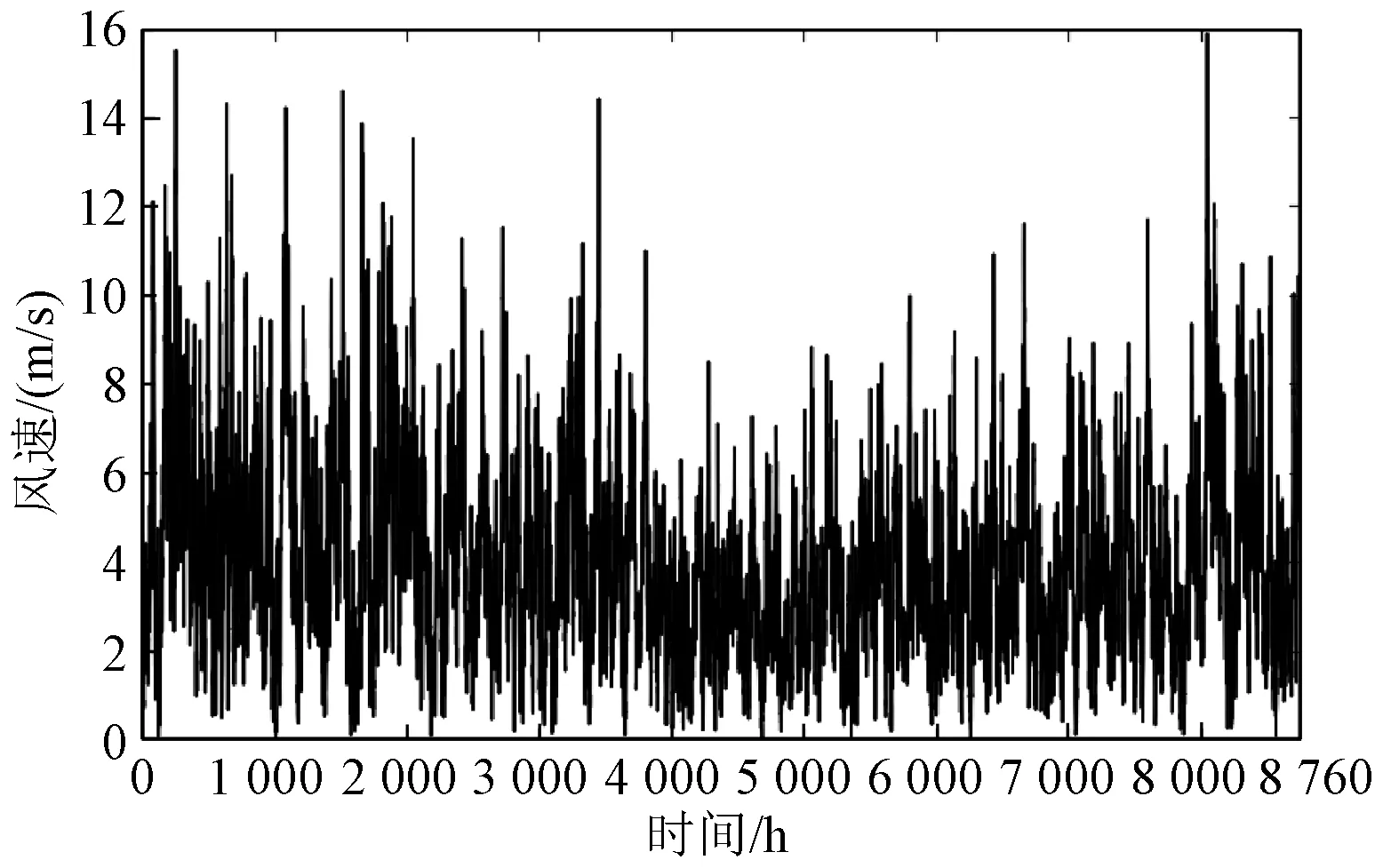
图5 全年风速曲线Fig.5 Annual wind speed curve

图6 全年负荷变化曲线Fig.6 Annual load change curve
设置微电网的寿命年限为20年,系统各分布式电源的参数见表1。
微电网在运行时所产生的主要污染物为柴油发电机发电时所排放的CO2、SO2和氮氧化物等,各种污染气体的排放参数见表2。
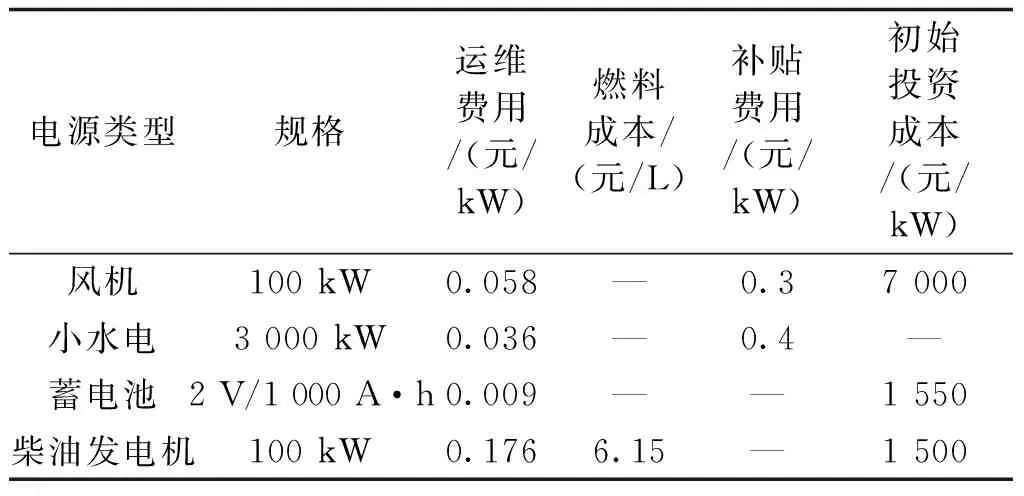
表1 系统设备参数Tab.1 System equipment parameters

表2 污染物排放参数Tab.2 Pollutant discharge parameters

表3 不同方案下微电网运行结果对比Tab.3 Comparison of microgrid operation results under different schemes
6.2 模型仿真结果与分析
为了便于比较分析,分别计算以下5种微电网优化配置和运行方案:
方案1:电价固定不变,不考虑DR,作为参照。取固定电价为0.85元/(kW·h),对优化配置模型进行求解,得到微电网最优容量配置。
方案2、3:在与方案1相同容量配置下,实行固定分时电价和动态分时电价,分别设为方案2、方案3,取峰谷电价分别为1.15元/(kW·h)和0.6元/(kW·h),计算DR后的负荷,并在其基础上计算微电网的经济效益和水风互补度。其中固定分时电价指经过长期统计负荷需求和新能源出力情况,将一天24 h划分为峰、谷两个固定时段。
方案4:实行动态分时电价,峰、谷电价分别取为1.15元/(kW·h)和0.6元/(kW·h),利用DR后的负荷以式(35)为目标函数求解微电网的最优容量配置。
方案5:实行动态分时电价,峰谷电价未知,与各分布式电源装机台数共同作为优化变量,以式(13)为目标函数求最佳峰谷电价,以式(35)为目标函数求微电网最优配置。
不同方案下微电网运行和优化配置的仿真结果见表3,不同方案下的评价指标结果见表4。
图7给出了方案1、方案2、方案3中实行固定电价、固定分时电价和动态分时电价时,在丰、枯水期某典型日的负荷变化以及可再生能源出力情况。
(1)比较方案1、方案2、方案3,分析在相同配置下不同电价机制对微电网运行结果的影响:
由图7和表3、表4可知,在实行固定分时电价和动态分时电价后,用户负荷根据电价引导进行了削峰填谷,提高了负荷贴近度,相较于固定电价,负荷贴近度分别提高了5.2%和11.8%,使负荷曲线与新能源出力曲线更加贴近,减少了系统中柴油发电机和蓄电池的使用,同时也降低了微电网从电网的购电量,进而使方案2、方案3的经济性优于方案1。方案2、方案3的可再生能源渗透率较方案1均有所提高,其中方案3的可再生能源渗透率最高,缓解了弃风、弃水现象。由于方案1、方案2、方案3的各分布式电源的配置相同,故三种方案的水风互补度相同。方案1作为参考方案,未考虑需求响应,故用户参与DR的满意度为1。

表4 不同方案下的评价指标Tab.4 Evaluation indicators under different schemes

图7 实施DR后负荷的变化情况Fig.7 Changes in load after implementation of DR
在经济性方面,相较于方案1,虽然方案2、方案3的供电收益均有所减少(即用户购电费用),分别减少了12.1万元和13.6万元,但同时方案2、方案3的与电网交互成本、运行维护成本、燃料成本和治污成本较方案1也都有所减少,方案2共减少了18.892万元,方案3共减少了26.893万元。综合来看,方案2、方案3的经济性要优于方案1,年运营收益分别提高了10.79万元和17.29万元。
因此,通过制定有效的电价机制,在微电网运行中实施DR,能够改善负荷特性,提高新能源消纳能力,既提高了微电网的经济性,又降低了用户购电费用,达到了供需两侧双赢的目的。相较于基于固定分时电价的DR,动态分时电价的效果更好,用户参与DR的满意度更高。
(2)比较方案1、方案4、方案5,分析DR对微电网优化配置结果的影响:
同方案1相比,方案4、方案5在计及DR参与微电网优化配置的情况下,风机装机容量有所增加,分别增加了200 kW和300 kW,蓄电池容量分别减少了132 kW·h和149 kW·h,柴油发电机发电量分别减少了7 292.36 kW·h和10 730.90 kW·h,系统与电网交互电量分别减少了25.05 MW·h和32.44 MW·h。从经济方面看,同方案1相比,方案4、方案5的用户购电费用分别减少了15.5万元和18.2万元,系统年运营收益分别增加了25.15万元和29.38万元。此外相比于方案1,方案4、方案5的可再生能源渗透率分别提高了12%和13.3%,负荷贴近度分别提高了16.2%和18.3%。可见,在微电网优化配置中计及DR的参与能够改善负荷特性,减少柴油发电机和蓄电池的使用,增加可再生能源的配置容量,提高可再生能源消纳水平,能够兼顾微电网的经济性与用户利益。
同方案3相比,方案4、方案5在用户购电费用减少的同时年运营收益均有所增加;可再生能源渗透率分别提高了1.9%和3.2%,用户满意度分别提高了3.7%和4.8%,负荷贴近度分别提高了4.4%和6.5%。因此,在微电网优化配置中计及DR的参与比确定分布式电源的容量配置后在微电网运行时考虑DR的结果要好。
(3)比较方案4、方案5,分析不同峰谷电价下的DR对微电网优化配置结果的影响:
图8给出了方案4、方案5在丰、枯水期某典型日的动态分时电价与负荷转移量的情况。可看出,相较于方案4采用的峰谷电价,方案5采用优化后的电价能更有效地调动用户参与DR的积极性,提高了负荷响应量,从而达到提高可再生能源消纳水平和缓解弃风、弃水的效果。优化后的峰谷电价分别为1.49元/(kW·h)和0.37元/(kW·h)。
分别在丰水期和枯水期内选取10天输出方案4、方案5中微电网与电网的交换功率、柴油发电机发电功率以及储能蓄电池功率变化曲线,如图9、图10所示。
由图9、图10和表3、表4可知,相较于方案4,方案5中风机装机容量有所增加,蓄电池、柴油发电机的使用以及从电网的购电量均有所降低。DR后的负荷与分布式电源的容量配置以及电价有关,同方案4相比,方案5不仅对分布式电源的容量配置进行了优化,还考虑了电价的优化,在迭代过程中,两者相互配合寻找最佳组合以使目标函数最优。最终优化结果为峰、谷电价分别为1.49元/(kW·h)和0.37元/(kW·h),在这种情况下,方案5的用户购电费用低于方案4,同时年运营收益、水风互补度、可再生能源渗透率以及负荷贴近度均高于方案4,同其他方案相比,方案5是最优方案。在基于DR参与的微电网优化配置中采取的电价不同,得到的优化结果也不同,合理的电价设置能够在提高微电网经济性的同时更好地保障用户利益,因此在计及DR参与的微电网优化配置中,有必要对电价进行优化。

图8 动态分时电价与负荷转移量Fig.8 Dynamic time-of-use electricity price and load transfer volume
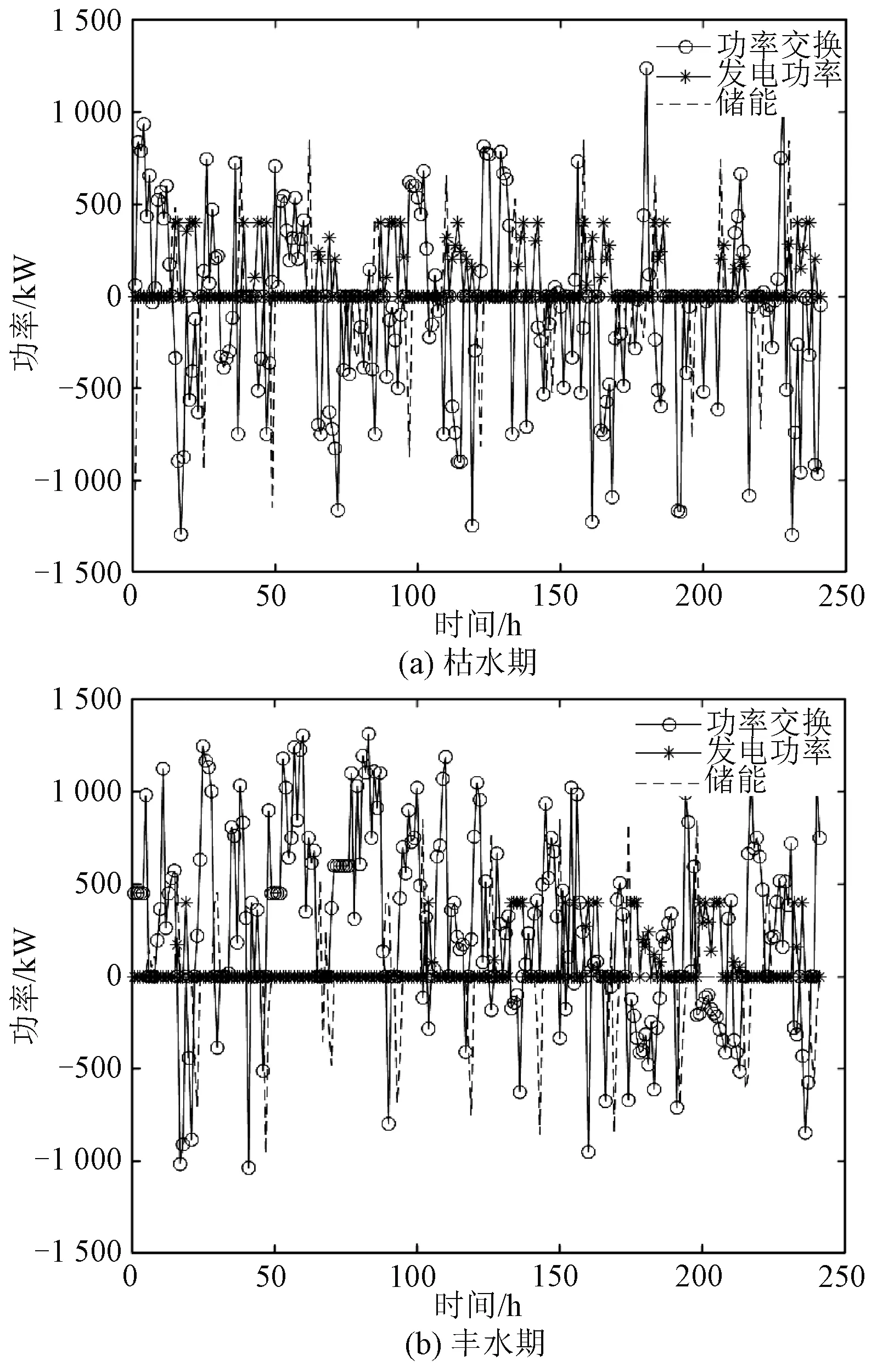
图9 方案4交换功率、柴油发电机发电功率以及储能电池功率变化曲线Fig.9 Schemes 4 power exchange, diesel generator power generation and energy storage battery power change curve

图10 方案5交换功率、柴油发电机发电功率以及储能电池功率变化曲线Fig.10 Schemes 5 power exchange, diesel generator power generation and energy storage battery power change curve
图11给出了方案1、方案4、方案5的全年水风互补度变化情况。

图11 全年互补度变化曲线Fig.11 Annual complementarity change curve
由表3可知,随着方案1、方案4、方案5中分布式电源装机容量的增加,γ值不断降低,使水风互补发电系统的输出功率更加稳定,有利于提高微电网的可靠性和可再生能源的消纳水平。由图11可以看出,丰水期的水风互补度要优于枯水期,说明丰水期水风互补发电的功率波动较枯水期要小。对比方案1~方案5可以证明水风互补性有利于提高微电网经济性,降低蓄电池的容量配置。
分别采用传统PSO算法和改进惯性权重的混沌粒子群算法(Improved Chaotic Particle Swarm Optimization with improved inertia weight,ICPSO)算法对方案5进行求解,图12给出了两种算法的适应度值变化曲线。
从图12可以看出采用ICPSO计算所得最优结果要优于采用PSO计算所得结果。PSO在计算过程中陷入了局部最优,而通过引入混沌扰动和Sigmoid函数对惯性权重进行实时调整得到的ICPSO,增强了传统PSO的全局搜索能力,有效地阻止了传统PSO陷入局部最优的情况,从而能够得到更优的结果。

图12 适应度值随迭代次数变化曲线Fig.12 Curve of fitness value with number of iterations
7 结论
本文以并网型水风互补微电网为研究对象,从发电端和负荷端两端入手,在引入价格型需求响应的基础上,构建了以年运营收益和水风互补度为优化目标的微电网优化配置模型,并在考虑水风互补效应的基础上,以提高系统经济性为目标制定了相应的运行控制策略。对于需求响应模型,进一步研究了动态分时电价方式,在引入更适合于峰谷电价机制的替代弹性的基础上,对负荷曲线进行动态峰谷时段划分,通过优化配置模型与需求响应模型的协调优化,寻找峰谷电价与分布式电源容量配置的最佳组合,以使目标函数最优。采用改进粒子群算法结合目标规划法对模型进行求解,相关结论如下:
(1)通过制定有效的电价机制,在微电网中实施DR,能够改善负荷特性,与只考虑发电侧优化相比,能够充分利用源荷两侧的资源,使可再生能源出力曲线与负荷需求曲线更加贴近,提高可再生能源的消纳能力,进而提高微电网的经济性。相较于基于固定分时电价的DR,动态分时电价的效果更好,用户参与DR的满意度更高。
(2)通过方案3、方案4、方案5的对比可知,在微电网优化配置中计及需求响应的参与比确定分布式电源的容量配置后在微电网运行时考虑需求响应的结果要好;通过方案4、方案5的对比可知,合理的电价设置能够在提高微电网经济性的同时更好地保障用户的利益,达到供需两侧双赢的目的。
(3)水风互补发电能够使可再生能源输出功率更加稳定,有利于提高微电网的经济性和可再生能源的消纳水平,降低蓄电池的配置容量。
(4)ICPSO能够有效克服传统PSO容易陷入局部最优的缺点,保证在计算过程中得到更优的结果。
