微通道内超临界氮气三维热流场实验与数值模拟
2022-03-03韩昌亮辛镜青于广滨刘俊秀许麒澳姚安卡尹鹏
韩昌亮,辛镜青,于广滨,刘俊秀,许麒澳,姚安卡,尹鹏
(1 哈尔滨理工大学机械动力工程学院,黑龙江 哈尔滨 150080; 2 航天海鹰(哈尔滨)钛业有限公司,黑龙江 哈尔滨 150029)
引 言
随着航天、船舶和能源等行业的发展,传统热交换器已经无法满足上述领域对换热器工作温度、压力和质量比等方面的要求[1-4]。通常情况下,微通道换热器因具有结构紧凑、换热量大[5-7]等特点被广泛应用于工程中[8-9]。 此外,超临界氮气(supercritical nitrogen,SCN2)具有安全、资源丰富和临界压力更低[10-11]等优点,通常被选为换热器内工作流体介质[12-13]。但是,由于SCN2在拟临界点附近热物性会发生剧烈的变化[14],并且微通道结构尺寸参数异于常规通道,尺寸效应作用使得微通道内超临界流体传热机理会呈现出不同的响应特征,导致已有的换热关联式对紧凑型微通道换热器设计适用性不强。因此,深入研究微通道内SCN2三维热流场特性对于换热器优化设计和高效安全运行意义重大。
现今,国内外学者对微通道内超临界流体对流传热特性开展了研究[15-18]。Zhu等[19]利用SSG雷诺应力模型研究了SCN2在垂直微细管中强化传热(HTE)现象,发现HTE 主要受层流底层和缓冲层影响。Fu 等[20]探讨了质量流速、管道直径等对微通道中超临界NOVEC 649对流传热特性的影响,发现对流传热系数随质量流速增加而增大,随着管道直径减小而增加。Rowinski 等[21]研究了非均匀热流施加于外壁时水从亚临界到超临界状态的变化规律,发现热通量越大,传热恶化现象越明显。Shang等[22]对不同直径水平管中超临界水对流传热特性进行了数值模拟,发现该对流传热过程受浮升力影响较大,且管径越大,传热恶化现象越容易发生。张宇等[23]通过数值模拟对低Reynolds 数条件下竖直圆管内超临界CO2对流换热现象进行了分析,结果表明LB 湍流模型可以较好地反映流体从层流向湍流过渡的现象。范辰浩等[24]通过实验对水平圆管内超临界水传热恶化特性进行了研究,结果表明小管径中由浮升力带来的“二次环流”对高流速超临界流体换热影响可以忽略。王军辉等[25]发现在流体温度达到拟临界温度之前存在一个强化传热区,且当液膜温度达到拟临界温度附近时,对流传热系数处于峰值区。
然而,目前绝大多数研究关注的是超临界流体在微通道轴向方向的传热规律,针对SCN2在不同圆周方向上的三维热流场研究较少,尤其是换热关联式的缺失,给微通道换热器优化设计带来了困难。针对这一问题,本文结合实验和数值模拟研究不同压力和质量流速对微通道内SCN2对流传热特性的影响,阐明不同圆周方向上三维热流场特征,探讨拟临界点附近径向热物性分布规律,分析浮升力的作用机理,提出新的无量纲换热关联式。
1 实验测试
整个实验系统由超低温液氮(LN2)供应系统、数据采集系统、换热系统和燃烧系统等组成。实验装置流程图如图1所示,其中,主要设备包括离心式鼓风机(最大体积流量为120 m3/h)、燃烧器(最大燃烧功率80 kW,北京热科技术有限公司)、增压泵(吸入压力0.02~0.8 MPa,最大排液压力15.5 MPa,流量30~120 L/h,杭州佳巨有限公司)和LN2杜瓦罐(公称工作压力为1.38 MPa,有效容积为209 L,美国查特公司)。为了降低实验系统热损失,利用绝热棉对水箱以及杜瓦罐和圆管入口之间管路进行包裹。

图1 实验装置流程图Fig.1 Flow chart of experimental device
实验过程中,首先关闭出口高压阀门,再开启增压泵,对LN2进行增压至超过其临界压力之后输送到换热系统中。空气量和燃料量由玻璃转子流量计(型号为LZB-40 和LZB-10,对应量程为10~60 L/h 和0.2~1 L/h)测量。在圆管进出口分别安装PT100 热电阻(量程为73~923 K,精度为0.35 K)测量LN2和SCN2温度,出口处安装质量流量计测量SCN2流量,并利用压力变送器(型号TRKYSG1K2BA3 压力/液位变送器,输出电流4~20 mA,精度0.3%FS,量程0~12 MPa)对圆管内压力进行监控。入口质量流速由气化后的SCN2折算得到。
表1 列举出了一组SCN2对流传热特性实验数据,为后续数值模拟提供了参考数据。可以看出,在恒定入口温度和压力工况下,质量流速增加到1.66 倍时,出口温度降低了8 K,圆管内SCN2对流传热系数增大,为原来的2.05 倍。有关实验系统的详细介绍,可以参考本课题组之前的研究[26-27]。
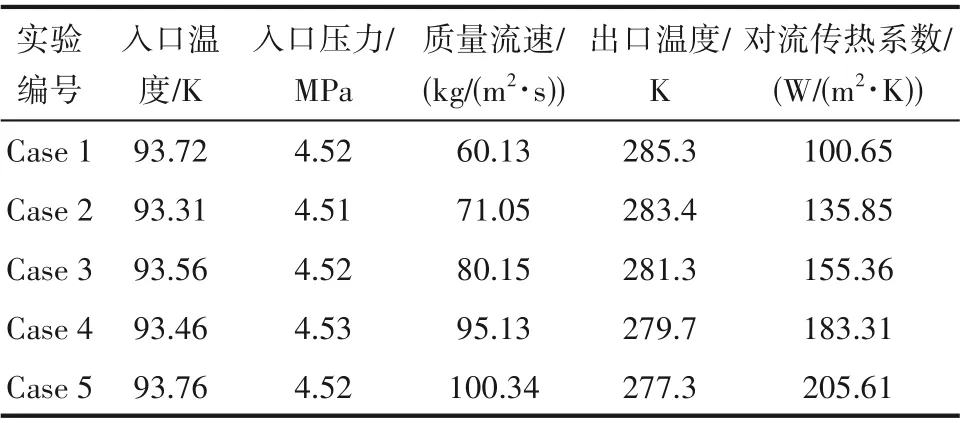
表1 SCN2对流传热特性实验参数Table 1 Convective heat transfer characteristic experimental parameters of SCN2
2 SCN2热流场数值模型
2.1 SCN2热物性分析
众所周知,超临界流体兼有液体和气体优点,并且在拟临界点附近物性参数会发生剧烈变化,使得其热传递现象与常规流体相比有很大差异[28]。图2 所示为利用美国国家标准技术研究所(NIST)获得的7 MPa 下SCN2热物性曲线。可以看出,在拟临界点(Tpc=142.7 K)附近SCN2热物性参数(密度、比定压热容、热导率和动力黏度)皆发生了剧烈的变化。其中,随着流体温度升高,密度、热导率和动力黏度均下降后缓慢平稳,而比定压热容呈先增大后减小,峰值出现在拟临界点处。
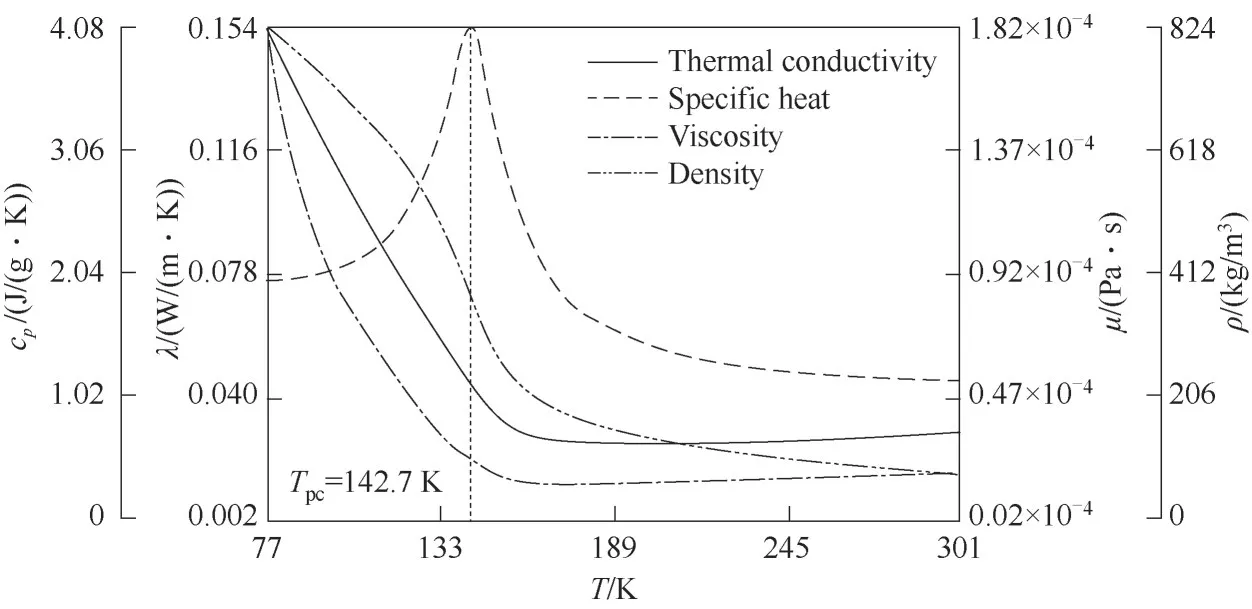
图2 7 MPa下SCN2热物性曲线Fig.2 Thermo-physical property of SCN2 under 7 MPa
2.2 物理模型和边界条件
为了研究微通道内SCN2三维热流场规律,建立了如图3 所示的三维物理模型。其中,微通道圆管内径为2 mm,外径为3 mm。为了使得SCN2达到完全湍流,整个物理模型分为60 mm 发展段、1000 mm实验段和60 mm 稳定段,采用水平方向布置方式。特别地,点1~5 取为圆管内壁面0°、45°、90°、135°和180°处位置。
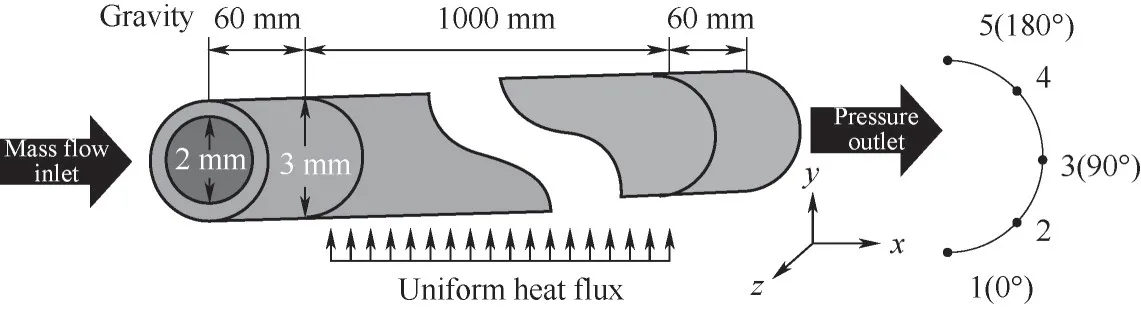
图3 物理模型Fig.3 Physical model
圆管入口为质量流速边界条件,出口为压力出口边界条件,圆管实验段外壁面设置为定热流第二类边界条件。重力加速度方向向下,并与SCN2流动方向保持垂直。此外,本文数值模拟基于表2 所示工况进行开展。
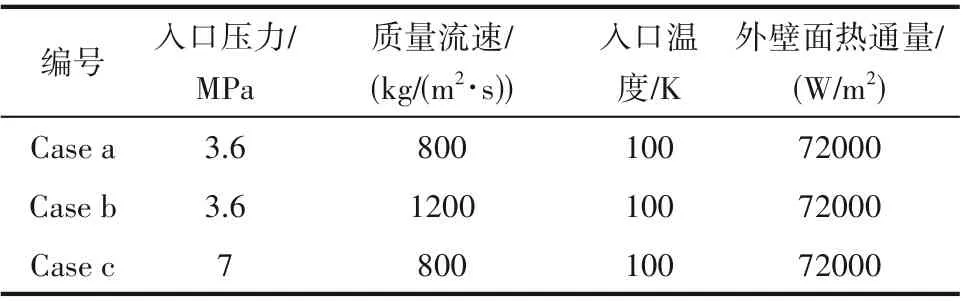
表2 数值模拟工况Table 2 Numerical simulation conditions
2.3 数学模型
SCN2对流传热过程可视为可压缩流体进行稳态离散化求解。其中,SCN2流态为完全发展湍流形式,可由质量、动量和能量控制方程来描述。

式中,Gk表示由于平均速度梯度产生的湍流动能;Gb是由于浮升力产生的湍流动能;YM表示可压缩湍流中的波动膨胀对整体耗散率的贡献。
2.4 数据处理方法
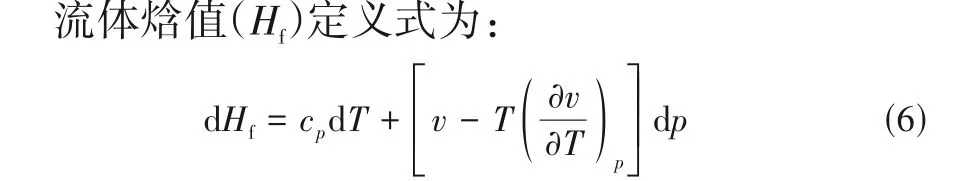
式中,v为流体体积。
Grashof 数(Gr)代表浮升力与黏性力比值,其定义式为:

其中,h为对流传热系数;l为特征长度;λ为流体热导率。
2.5 网格生成和数值方法
采用Ansys 16.0 商用软件对上述一系列控制方程进行离散化求解,利用ICEM 软件对上述物理模型流体区域进行O 型网格划分,具体情况如图4 所示。由于固体壁面内部热传递方式仅为热传导,网格设置相对稀疏。此外,为了准确捕捉圆管近壁面SCN2复杂的对流传热特性,将第一层网格设置在黏性底层外,计算过程中壁面y+>30,满足数值计算需求。压力与速度耦合采用SIMPLE 算法求解,基于压力求解器对动量、湍动能、湍流耗散率和能量方程离散化,均采用二阶迎风差分格式以保证数值计算的精确性。建立5 套网格系统,通过考察不同网格节点距离下的局部SCN2传热系数变化规律,以此来验证网格无关性,最终本文总体网格数目为7724332,流体和固体区域最小节点距离均为0.039。
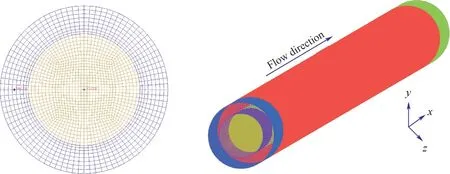
图4 网格示意图Fig.4 Sketch map of mesh
2.6 模拟结果与实验数据对比验证
为了验证数值方法准确性,将模拟结果与表1实验数据进行对比分析。图5 所示为入口温度93.46 K,入口压力4.52 MPa 工况时,SCN2出口温度和对流传热系数随着入口质量流速变化趋势。可以看出,两者的变化趋势保持一致,相对误差小于10%,满足工程实际需求。两者误差来源一方面在于SCN2热物性参数是在恒定压力下进行拟合得到的,忽略了压力损失对热物性的影响。另一方面在于实验过程中,必定会存在热量损失,而数值模拟是按照理论情况下流体升温热量计算所得。说明了本文所示数值方法能够较好地反映SCN2对流传热特性,可以进一步地开展微通道内SCN2三维热流场分析和研究。
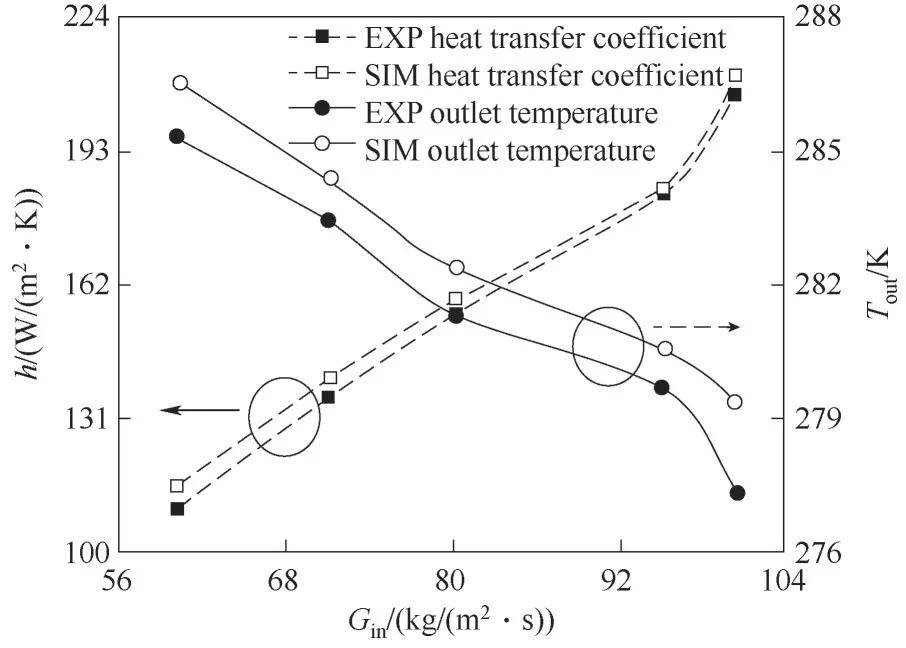
图5 数值结果与实验值对比Fig.5 Comparison between numerical results and experimental data
3 结果和讨论
3.1 内壁温分析
图6所示为不同压力和质量流速下微通道内壁温随流体焓值分布曲线。可以看出,在工况a下,受浮升力和重力双重作用,同一轴向截面位置处,圆管径向内壁温呈现较大温差,内壁温最小值出现在0°位置处。进一步地,当Hf,pc=30.65 kJ/kg 时,180°处内壁温高于0°处,两者之间温差呈现13.33 K响应特征。随着质量流速增加(工况b),内壁温最大值由180°处向90°位置处发生偏移,原因是此时SCN2轴向速度增大,减小了SCN2速度矢量的y、z方向分量,进而减弱了加速度引起的湍流阻尼效应。在工况c下,随着压力的升高,拟临界流体焓值附近SCN2比定压热容峰值减小,吸热能力减弱,导致内壁温差变小。
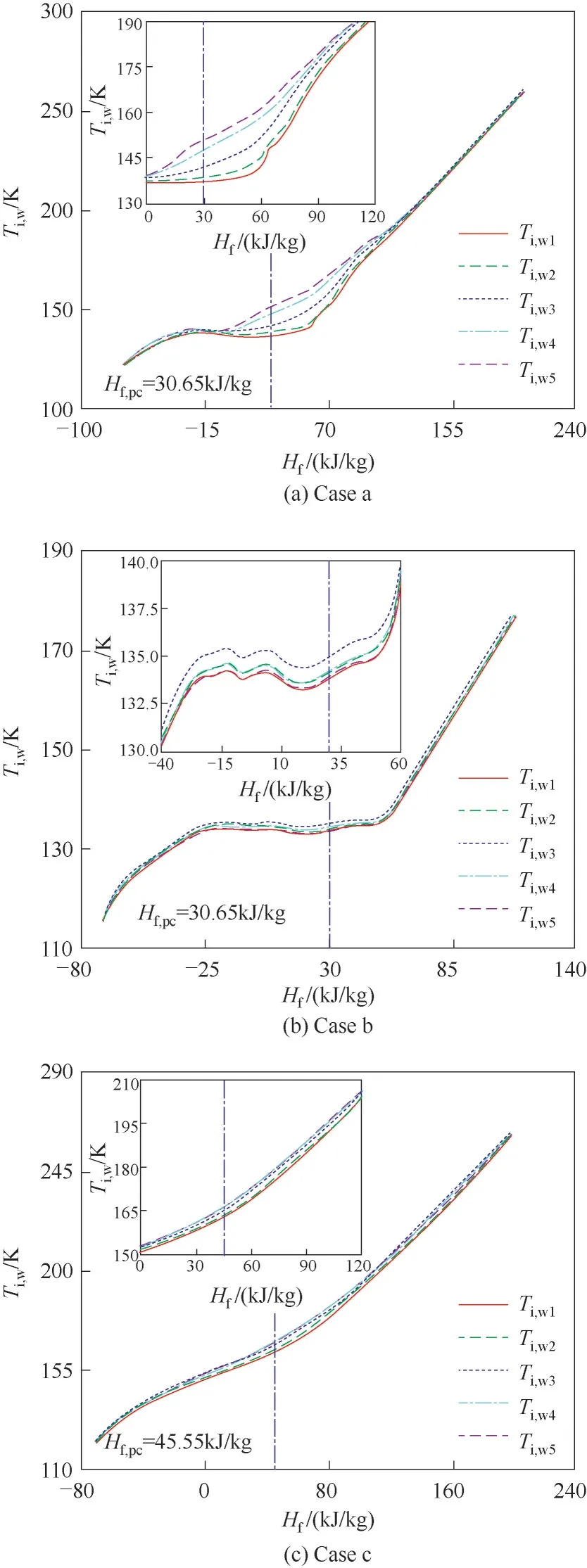
图6 压力和质量流速对内壁温的影响Fig.6 Effect of pressure and mass flux on inner wall temperature
图7 为不同压力和质量流速下比定压热容以及对流传热系数随流体温度与临界温度比值变化曲线。可以看出,SCN2对流传热系数均呈先增大后减小,峰值出现在拟临界温度附近。随着质量流速越大,流体边界层厚度减薄,SCN2对流传热系数峰值由11443.01 W/(m2·K)增加到18090.31 W/(m2·K),并且对流传热系数最小值逐渐从圆管180°处向圆管90°处转移。此外,随着压力升高,比定压热容峰值减小,导致SCN2径向对流传热系数差值变小。所有工况下,圆管0°处对流传热系数皆最大,原因是圆管下部区域流体与内壁面之间温差较小。
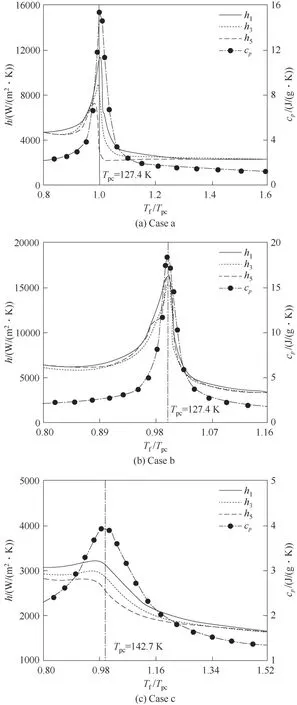
图7 压力和质量流速对比定压热容和对流传热系数的影响Fig.7 Effect of pressure and mass flux on specific heat and heat transfer coefficient
3.2 拟临界点附近热流场分析
图8所示为三个工况下拟临界点附近径向速度矢量图和y方向速度云图。可以看出,受浮升力影响,拟临界点附近处SCN2由底部向上部流动。同时,重力驱使SCN2向下流动,进而形成了“二次环流”,强化了SCN2和内壁面之间对流传热强度。由图8(a)可以看出,在低压力和低质量流速工况下,密度差引起的浮升力使得SCN2径向速度达到了0.0316 m/s。此外,y方向速度呈两侧较高中部低现象。说明SCN2对流传热过程中,相比于重力而言,浮升力占据主导地位。
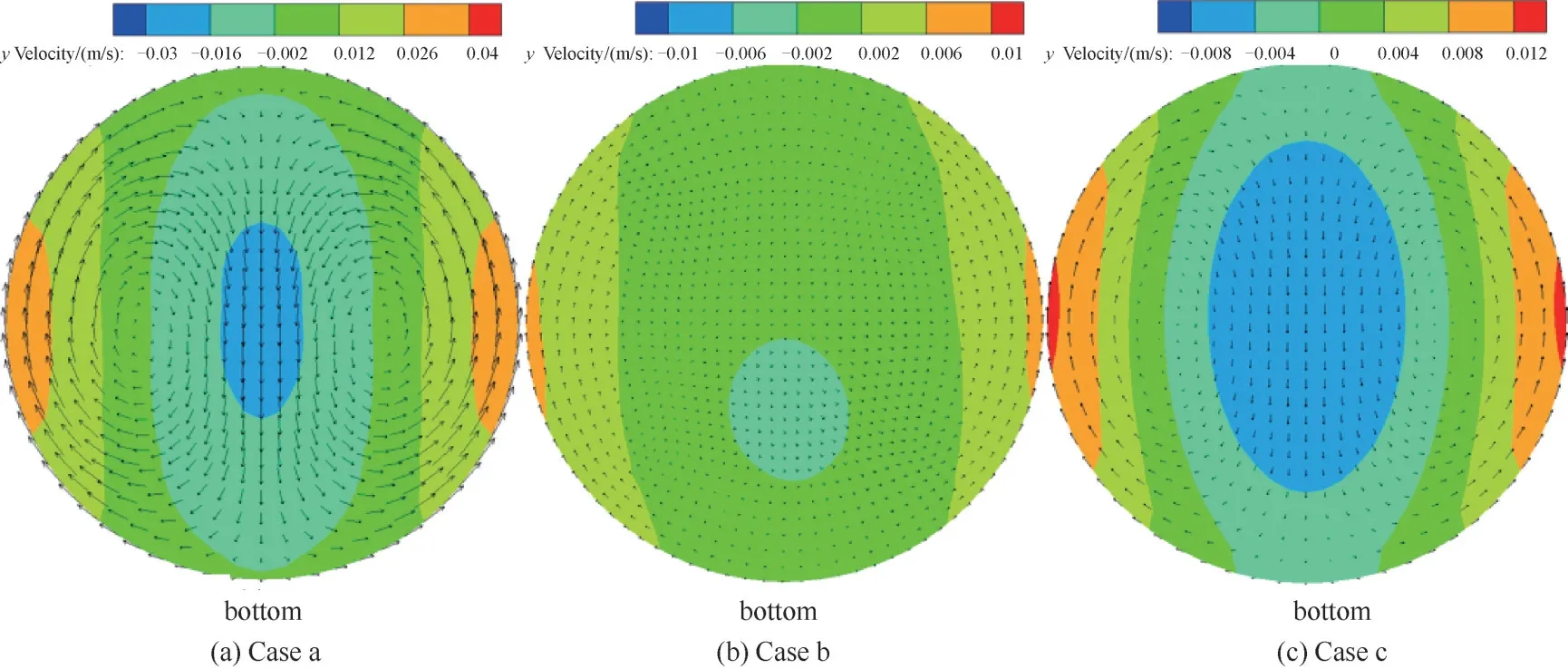
图8 拟临界点附近SCN2径向速度和y方向速度分布Fig.8 Distribution of SCN2 radial velocity and y-direction velocity near pseudo-critical point
图9 给出了在拟临界点附近SCN2热物性云图分布。由图可得,靠近圆管内壁处SCN2温度远高于其他区域,形成了径向密度差,进而产生了较大的浮升力,使得SCN2沿管内壁附近逐渐向上流动。进一步地,湍流黏度最大值出现在圆管中心偏下处。此外,由于SCN2热物性主要受温度场的影响,使得SCN2在低密度区域处热导率也较小,圆管上部流体导热能力较弱,该区域内SCN2与内壁面之间传热能力减弱。
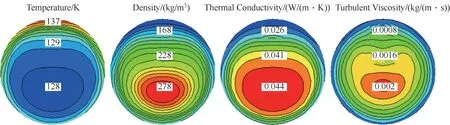
图9 拟临界点附近SCN2热物性分布Fig.9 Distribution of SCN2 thermo-physical properties near the pseudo-critical point
3.3 浮升力预测
Metais 等[29]提出可以用Gr/Re2<0.1 来判断湍流浮升力对流体传热的影响,当比值小于0.1 时可忽略浮升力作用。特别指出,对于恒定壁面热通量而言,由于圆管壁温未知,可以用修正Gr*[30]来计算,计算公式如下:

图10 中为不同压力和质量流速下浮升力系数沿轴向变化曲线。可以看出,沿着微通道圆管轴向方向,浮升力系数(Gr*/Re2)呈先增大后减小变化,该现象主要是由SCN2热物性导致。当Gr*/Re2>0.1时,SCN2对流传热机制为混合对流。特别地,在HTE 段内,Gr*/Re2增长速率减缓。当Gr*/Re2>1 时,相比于圆管上部区域,圆管底部强化传热更为明显。随着压力和质量流速增大,Gr*/Re2峰值降低,使得浮升力作用逐渐减弱。
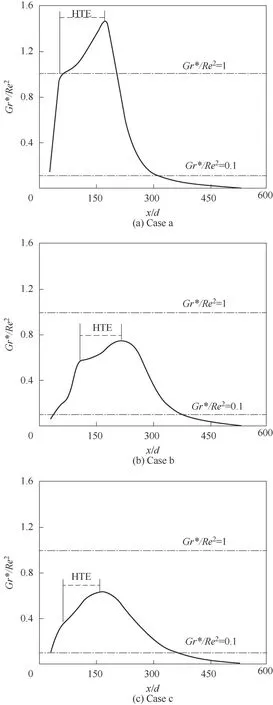
图10 浮升力系数沿轴向分布Fig.10 Distribution of buoyancy coefficient along the axial direction
3.4 新的无量纲换热关联式拟合
目前,常用于预测微通道内SCN2对流传热特性无量纲换热关联式如表3 所示。其中,相比于Dittus-Boelter 关联式,Tatsumoto 关联式和Zhao 关联式预测偏差分别为49%和34%,误差均较大。

表3 常用预测SCN2对流传热无量纲换热关联式Table 3 Common dimensionless correlations for predicting convective heat transfer of SCN2
鉴于此,本文使用无量纲分析法提出一个新的适用于预测微通道内SCN2对流传热特性无量纲换热关联式。鉴于浮升力影响不可忽略,本文引入Gr*项,该关联式基本形式如下:

其中,Cb为温差修正系数;μw为壁温下流体黏度。该关联式适用范围为:3.6 MPa ≤p≤7 MPa,1.8 × 104 图11 为利用本文拟合所得的新关联式预测值与模拟值的对比。可以看出,本文关联式预测精度较高,所有Nusselt 数预测值与模拟值偏差均小于20%,新的关联式可以较好地预测3.6~7 MPa下微通道内SCN2热流场特性,为微通道换热器优化设计提供了参考依据。 图11 Nusselt数模拟值与预测值对比Fig.11 Comparison of simulated and predicted Nusselt number 本文结合实验和数值模拟方法对微通道内SCN2三维热流场进行了研究,利用实验数据验证了数值模拟模型和方法准确性,得到了以下主要结论。 (1)微通道内SCN2换热过程中,同一轴向截面位置处,圆管径向内壁温呈较大温差,内壁温最小值均出现在0°位置处。随着质量流速增加,内壁温最大值和对流传热系数最小值由180°处向90°位置处发生了偏移。对流传热系数峰值出现在拟临界温度附近。随着压力升高,微通道圆管内壁温差和径向SCN2对流传热系数差值均变小。 (2)受浮升力和重力影响,SCN2在临界点附近处形成了“二次环流”,强化了SCN2和内壁面之间对流传热强度。圆管内径向SCN2热物性均呈不均匀分布。圆管上部区域内的SCN2传热能力较弱,易出现传热恶化现象。当Gr*/Re2>1时,浮升力对圆管底部区域SCN2强化传热作用更明显。 (3)提出了一个新的可用于预测微通道圆管内SCN2在3.6~7 MPa 对流传热特性的无量纲换热关联式,预测偏差小于20%,可以为以SCN2为流体介质的微通道换热器优化设计提供参考依据。 符 号 说 明 cp——比定压热容,J/(g∙K) d——内直径,mm G——质量流速,kg/(m2∙s) Gr——Grashof数 Gr*——修正的Grashof数 H——流体焓值,kJ/kg h——传热系数,W/(m2∙K) Nu——Nusselt数 p——压力,MPa Re——Reynolds数 T——温度,K x——轴向距离,mm λ——热导率,W/(m∙K) μ——动力黏度,Pa∙s ρ——密度,kg/m3 下角标 f——流体 i,w——内壁面 in——入口 out——出口 pc——拟临界 pred——预测 sim——模拟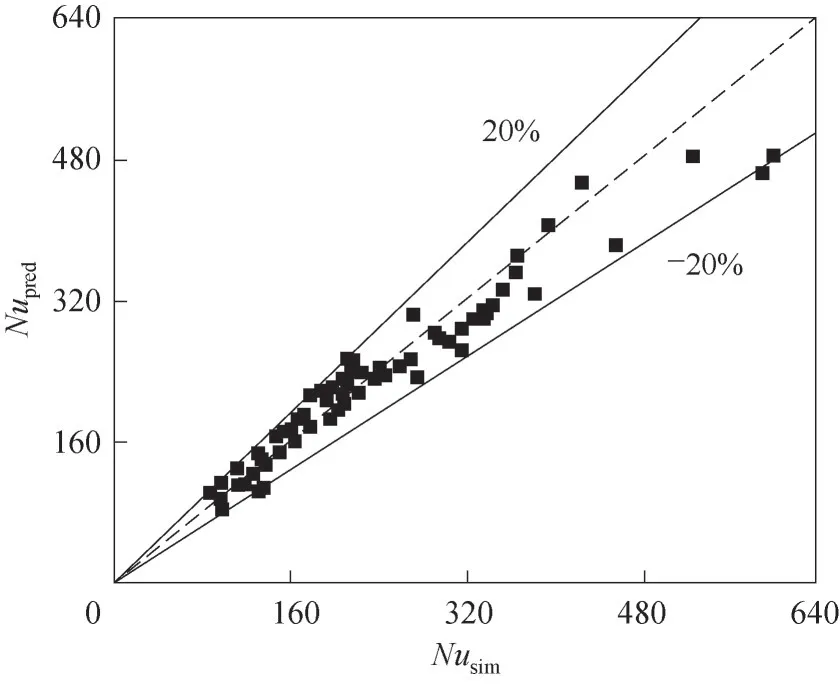
4 结 论
