起伏振动倾斜上升管气液两相流摩擦阻力分析与计算
2022-03-03周云龙刘起超
周云龙,刘起超
(东北电力大学能源与动力工程学院,吉林省 吉林市 132012)
引 言
气液两相流是日常生活和工业生产中常见的流动现象,其中摩擦压降的准确计算对设备安全运行有重要的意义[1]。经过广大学者多年研究,在静止管道气液两相流摩擦压降的计算方面取得了一系列的成果,建立了基于分相模型和均相模型的摩擦压降计算关系式[2-10]。
随着海洋核动力的发展,运动管道的气液两相流动特性成为研究热点。管道的运动可以简单分为摇摆、起伏和水平运动。高璞珍等[11]对海洋条件下核动力装置一回路冷却剂的流动压降进行研究,得出了海洋条件引起的不同运动类型单相流附加压降计算模型,为海洋条件下摩擦阻力的计算提供理论参考。
众多学者对摇摆状态的阻力特性进行了比较充分的研究,Xing 等[12-13]对不同摇摆参数和水泵压头下矩形管道单相流摩擦阻力进行研究,发现低流量下摩擦阻力受摇摆运动的影响较大,静止管道的计算方法不再适用,结合理论分析建立了适用于摇摆运动的单相流摩擦压降计算模型。曹夏昕等[14]在摇摆状态下竖直圆管内单相水的阻力特性研究中发现摩擦阻力系数周期性波动,其瞬时值与摇摆周期成正比,而摇摆幅度影响较小。张金红等[15]引入摇摆雷诺数,通过对实验数据的拟合建立了摇摆状态水平管单相水摩擦阻力系数计算模型。
Yu 等[16]采用快速傅里叶变换对摇摆状态窄矩形通道气液两相流动压差信号进行分析,成功在压差信号中提取出了摇摆信号,揭示了摇摆参数和压差信号间的耦合机理。张金红[17]、栾锋[18]、刘传成等[19]和Jin 等[20]分别对摇摆状态下不同类型管道和不同流型的摩擦阻力特性进行研究,建立了适用于摇摆状态的气液两相流摩擦压降计算模型。
针对起伏振动下管内流动和传热特性,Li 等[21]和Iliuta 等[22]采用数值模拟方法对起伏振动下不同管道内碳氢化合物的压降进行分析,但仅得出了压降随振动的变化趋势。Pendyala 等[23]在振动频率0.1~1 Hz、振幅0.125 m 范围内对雷诺数在500~6500的上升管单相水流动压降进行了研究,建立了基于雷诺数的摩擦压降计算模型。Li 等[24]、Hong 等[25]和Yu 等[26]分别对起伏振动下不同管内的传热特性进行实验和数值研究,发现起伏振动能在一定程度上增强换热效果,并建立了适用于振动条件的传热系数计算模型。周云龙等研究了起伏振动倾斜管单相流[27]和水平管气液两相流[28-29]摩擦压降变化规律,评价了现有摩擦压降计算模型在起伏振动水平管中的适用性,建立了起伏振动倾斜管单相流摩擦压降计算关系式。
在海洋条件下经常出现倾斜管的起伏振动,然而尚未有学者建立起伏振动倾斜上升管气液两相流摩擦压降的计算关系式。本文对不同流动和振动工况下倾斜管内气液两相流动摩擦压降进行实验研究,分析起伏振动下倾斜管摩擦压降动力特性,评价静止管道计算模型的适用性,揭示流动和振动参数对摩擦压降的影响规律,建立适用于起伏振动倾斜管的气液两相流摩擦压降计算关系式,对海洋核动力装置的正确设计和安全运行有重要意义。
1 实验系统
1.1 实验系统简介
实验系统由气水两相流循环回路、实验段、起伏振动实验台和压差测量单元组成,如图1 所示。实验所需的空气和水分别由空气压缩机和水泵供给,气相回路和液相回路都配备有旁路,便于实验系统压力的调整。空气和水在带有均匀板的相混合器中进行混合,然后以气液两相流的形式进入实验段。实验段为长1.4 m 的有机玻璃管。文献[30]指出,一般海洋运输船的极限倾角大多在20 多度,为了充分考虑倾角对摩擦阻力的影响,本文选择倾斜角度(θ)为30°,内径(d)为20 mm,在两端布置间距(L)为0.8 m 的两个测压孔,实验段的压差采用动态差压变送器测量。
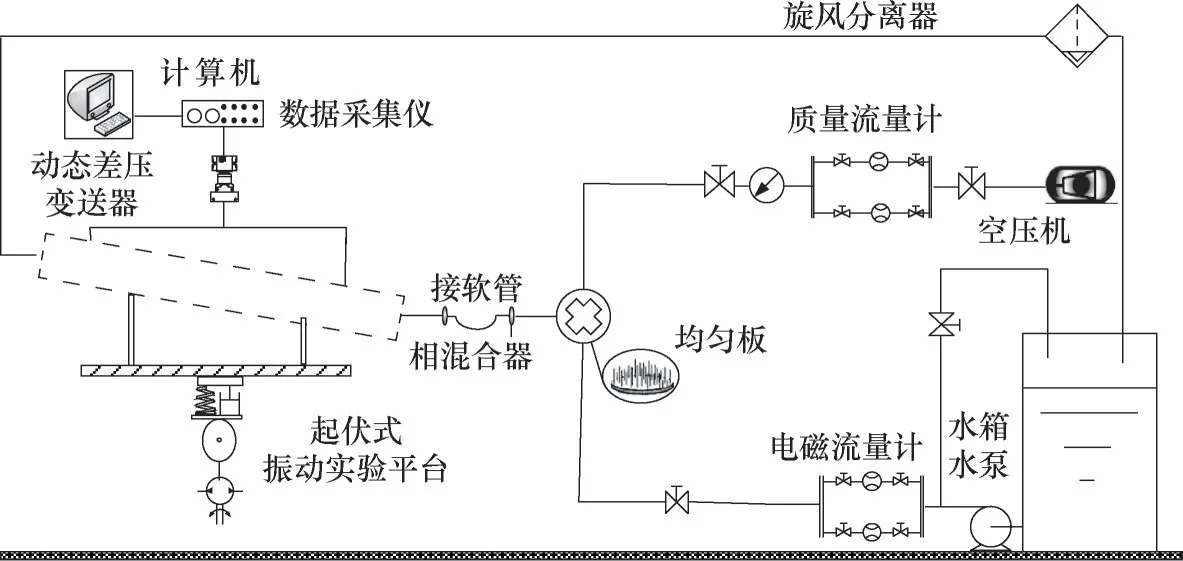
图1 实验系统Fig.1 Experimental system
起伏振动实验台的位移(Z)可以用式(1)表示:

振动速度(v)和振动加速度(a)可对Z求导得出。鉴于海洋条件下振动以低频高幅为主,结合振动台参数限制,本文选取振幅(A)为2、5 和8 mm,频率(f)为2、5和8 Hz。
1.2 误差分析
实验误差主要来源于电磁流量计、质量流量计和差压传感器。实验误差采用不确定度方法进行分析,主要包括A类不确定度和B类不确定度,参照文献[31]计算三种测量仪表的不确定度,如表1所示。
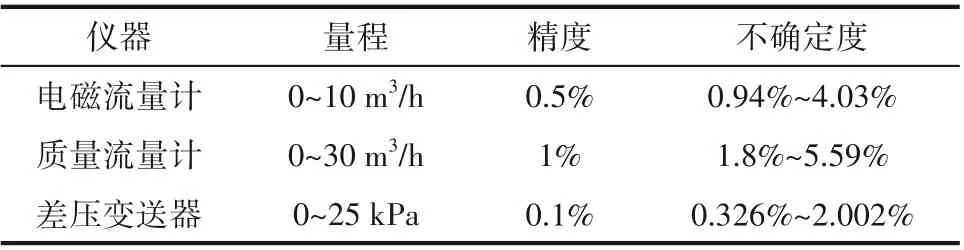
表1 实验仪器及不确定度Table 1 Experimental instrument and uncertainty
2 数据处理
两相流在静止直管内的流动总压降由摩擦压降、重位压降和加速压降三部分组成,在起伏振动状态下,由起伏振动引起附加压降,实验在常温下进行,温度变化可忽略不计,加速压降为零,流动的总压降如式(2)所示:

式中,P为总压降,Pa;Pf为摩擦压降,Pa;PG为重位压降,Pa;Padd为附加压降,Pa。
摩擦阻力系数的计算仍然采用达西公式:

式中,λv为起伏振动摩擦阻力系数;V为两相混合物平均速度,m/s。
2.1 摩擦压降计算
摩擦压降的计算模型主要分为均相模型和分相模型,采用不同模型进行计算,验证其在起伏振动状态下的适用性。
2.1.1 均相模型 均相模型摩擦压降的计算如式(4)所示:
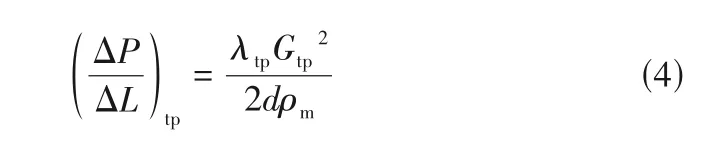
式中,Gtp为两相质量流速,kg/(m2·s);ρm为两相流动密度,kg/m3。
实验段采用有机玻璃管道,粗糙度很小,且均相雷诺数范围为5166~83722,在典型尼古拉兹曲线中处于紊流水力光滑管区,摩擦阻力系数可用式(5)计算:

针对两相动力黏度μtp的计算,学者们提出了不同的计算方法,典型的如表2所示。

表2 两相动力黏度计算模型Table 2 Calculation model of two phase dynamic viscosity
2.1.2 分相模型 Lockhart 等[7]首次提出了用于气液两相流摩擦压降计算的分相模型,该模型定义了分液相系数和分气相系数,如式(6)和式(7)所示。


2.2 重位压降计算
重位压降的计算如式(13)所示。

2.3 附加压降计算
根据高璞珍等[11]的研究,起伏振动引起的附加压降可用式(15)表示。
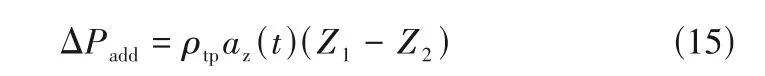
式中,az(t)为振动加速度,m/s2;(Z1-Z2)为垂直振动方向上沿流动方向起点和终点的位移,m。
3 结果与讨论
3.1 静止管道计算模型评价
由于目前起伏振动倾斜管摩擦压降研究几乎处于空白,静止管道的计算模型是否适用于起伏振动管道尚未证实。选取包含所有振动工况和流型的163 组数据,分别采用上述均相模型和分相模型对摩擦阻力系数进行计算,并与实验值进行对比,结果如图2 所示。由图可知,上述7 种计算模型的计算结果误差分布比较分散,范围均超过了-30%~30%,并且误差范围在-15%~15%的数据相对较少。随着摩擦阻力系数的增大,平均误差超出30%的比例越大。
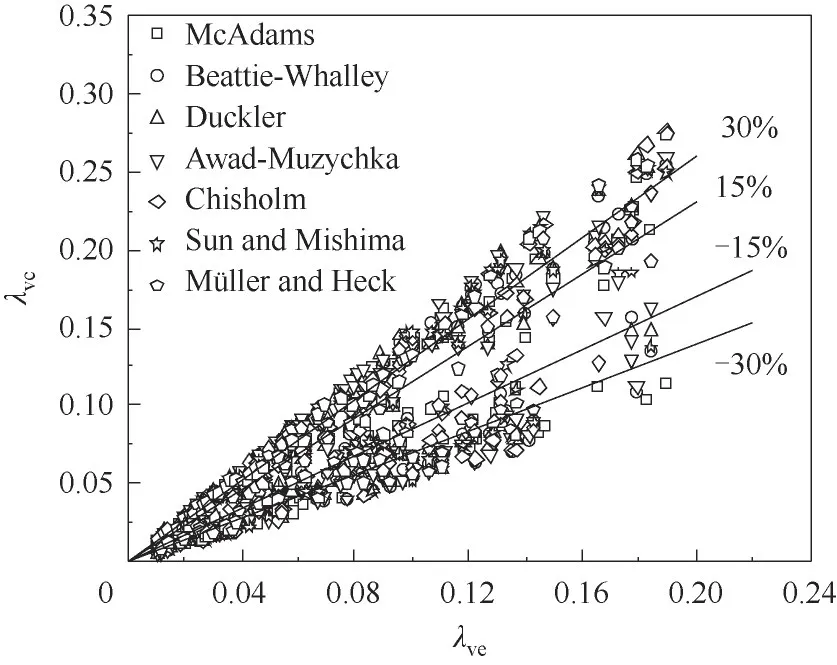
图2 静止管道不同模型计算误差分布Fig.2 Calculation errors distribution of different models of static pipe
为了客观评价模型的适用性,采用绝对误差平均值(EMA)作为评价指标,如式(16)所示。
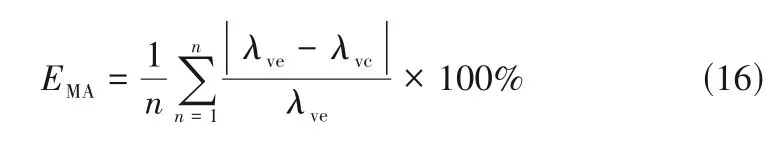
式中,n为数据总量,163。
不同模型的误差平均值如表3 所示。由表可知,分相模型和均相模型计算得到的误差平均值相近,都在30%左右,其中以Müller and Heck 模型最小,为27.22%,30%以内误差所占比例为51.53%。这表明静止管道下得出的摩擦压降计算模型不能用于起伏振动。均相模型中McAdams 模型得到的误差平均值最小,为27.86%,且30%以内误差所占比例最高,为47.85%,因此后续分析中均相雷诺数的计算采用McAdams模型。

表3 静止管道不同模型计算值与实验值误差Table 3 The errors between calculated values of different models and experimental values in static pipe
3.2 起伏振动对摩擦压降的影响
管道的起伏振动会对管内流体微团引入附加力,改变流体的运动情况,进而影响气液两相流摩擦压降。图3 所示为Jg=0.1 m/s、Jw=2.6 m/s、f=5 Hz、A=5 mm 时起伏振动和静止状态的摩擦压降。由图可知,管道的起伏振动使气液两相流摩擦压降的波动加剧,并且导致平均摩擦压降增大。与静止管道相比,f=5 Hz、A=5 mm 时的摩擦压降平均值增加了52%,如果按照静止管道的摩擦压降进行计算,将会大大低估了管道中的摩擦压降。在锅炉水冷壁或蒸汽发生器中可能出现循环停滞或者循环倒流,进而发生严重故障,这也说明了对起伏振动下管内气液两相流动摩擦压降研究的必要性。
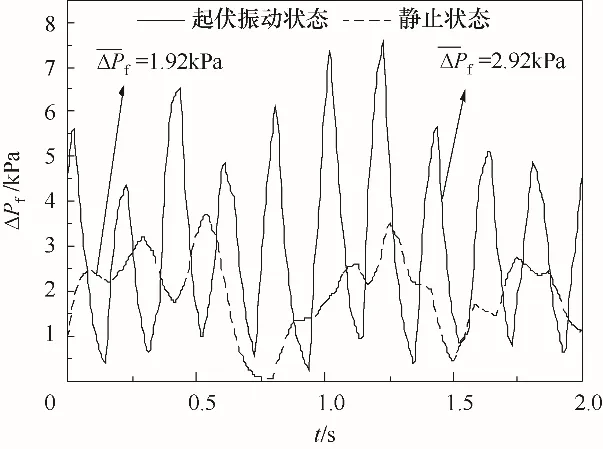
图3 静止和起伏振动管道摩擦压降波动Fig.3 Friction pressure drop fluctuation of static and fluctuating vibration pipe
分别对起伏振动状态和静止状态的摩擦压降进行功率谱分析,如图4所示。结果表明,静止状态的摩擦压降波动规律性不明显,没有显著的波动主频率,而起伏振动状态下的摩擦压降波动规律性较强,具有多个显著的频率,文献[16]在摇摆状态下的气液两相流摩擦阻力特性分析中也发现了类似的波动规律。这说明起伏振动会导致摩擦压降周期性波动,摩擦阻力系数是和运动参数相关的变量。
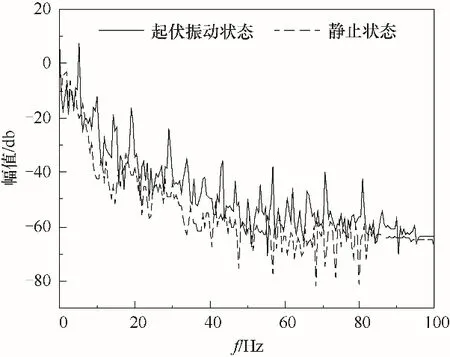
图4 静止和起伏振动管道摩擦压降功率谱Fig.4 Power spectrum of frictional pressure drop in static and fluctuating vibration pipeline
多尺度熵能够反映气液两相流动的复杂程度,是分析流动不稳定性的重要手段。对f=5 Hz、A=5 mm 振动状态以及静止状态不同气相和液相折算速度下的摩擦压降进行多尺度熵分析,模板长度m=2,匹配阈值r=0.2,求取前25 个尺度的熵值,如图5所示。
图5结果表明,当流型为泡状流时,起伏振动摩擦压降熵值低于静止管道。此时,液相占比大且流速快,气泡弥散分布于液相中,在交替附加力的作用下,气泡分布区域集中在管道轴线上方区域,并且小气泡逐渐破裂合并成大气泡,与静止管道相比,气泡运动随机性较小,熵值降低。当流型为弹状流或环状流时,起伏振动摩擦压降熵值高于静止管道。此时,气相以气弹或气芯形式存在,液相含量较少,在交替附加力的作用下容易发生气弹破碎与合并以及液环和气芯之间的互相侵入,使得弹状流和环状流流动更加复杂,熵值增大。从图中还可发现静止管道的熵值变化趋势比较稳定,随尺度的增加呈上升趋势,而起伏振动下的熵值在尺度为8、10和20处都出现明显转折,说明起伏振动下流动更加不稳定,导致摩擦压降增大。
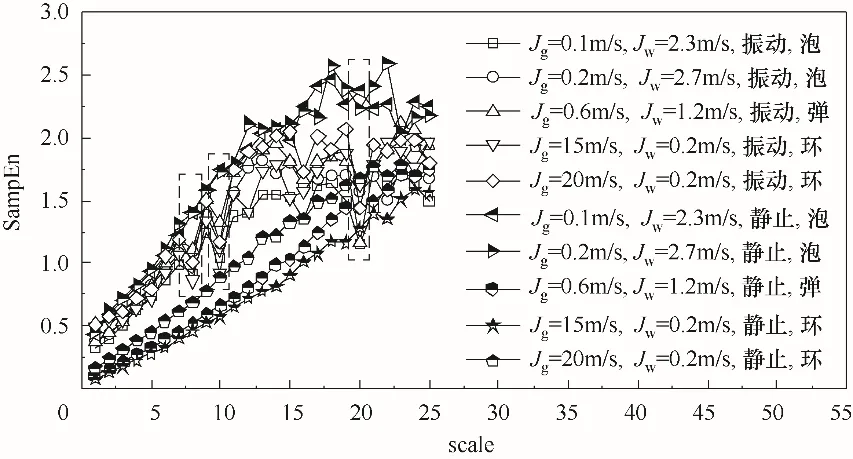
图5 不同流动工况起伏和静止管道摩擦压降多尺度熵Fig.5 Multi scale entropy of frictional pressure drop in fluctuating and stationary pipes under different flow conditions
Jg=0.1 m/s、Jw=2.6 m/s、f=5 Hz、A=5 mm时振动加速度和瞬时摩擦压降波动以及对应的频率分析如图6所示。从图中可以明显看出起伏振动下摩擦压降的波动规律与管道振动加速度变化规律基本一致,并且在振动过程中伴随着气泡的破裂和重新聚合,导致流体微团与壁面的接触受力最大时刻与加速度最大时刻有所偏差,摩擦压降与加速度的峰谷值出现时间相比有一定的提前或者延后。从频谱图中可以看出摩擦压降信号中存在明显的5 Hz 频率分量,该频率与振动频率一致,这说明起伏振动状态下摩擦压降的波动主频率取决于振动频率。
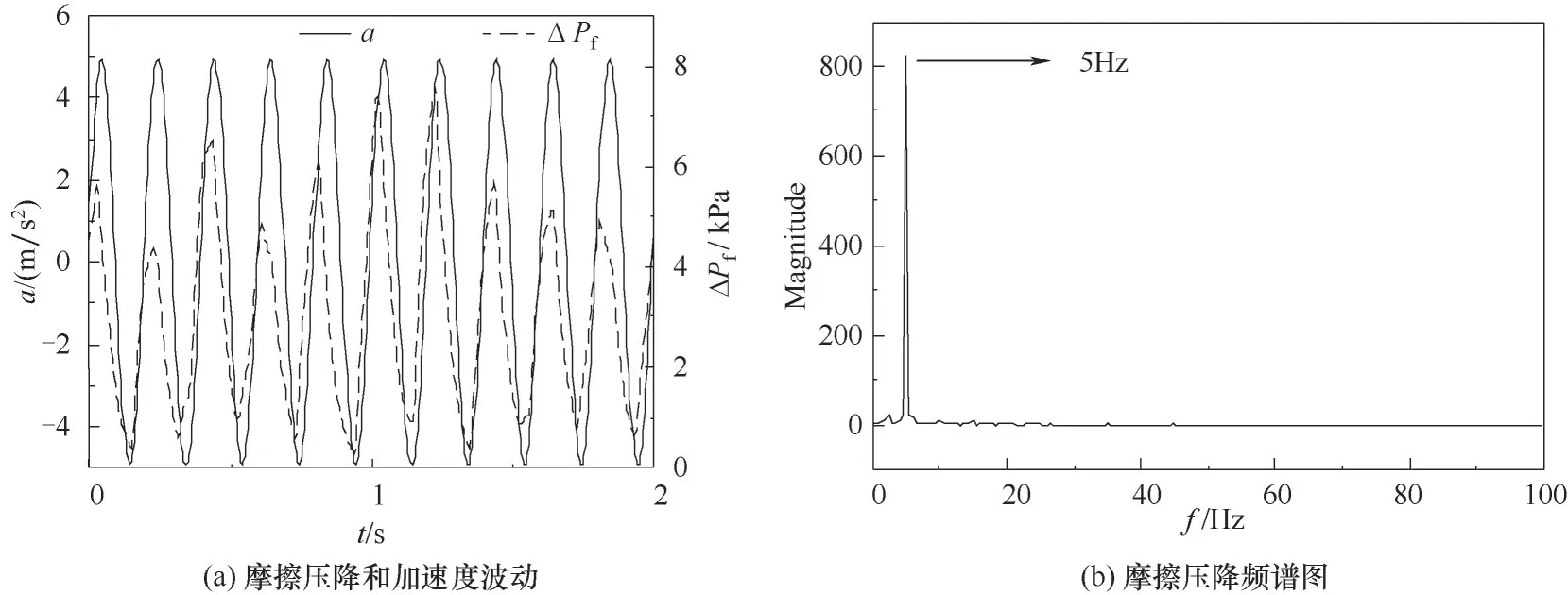
图6 振动加速度和摩擦压降波动及频率分析Fig.6 Vibration acceleration and friction pressure drop fluctuation and frequency analysis
3.3 两相雷诺数对摩擦阻力系数的影响
相同振动工况、不同雷诺数下摩擦阻力系数波动如图7所示。由图可知,在不同振动规律下,摩擦阻力系数都与雷诺数成反比。f=2 Hz、A=2 mm 时随着雷诺数从11269增至51622,摩擦阻力系数平均值由0.209降至0.014。此外,随着振动加剧,摩擦阻力系数的波动程度变大,并且当f=8 Hz、A=5 mm 时出现摩擦阻力系数为负值的现象。这是因为随着振动加剧,作用于流体微团上的附加作用力逐渐增大,当其和重力沿流动方向的分力大于流动的动力时就会出现短暂的倒流现象,在设计时要适当增大泵的压头,防止因为振动而出现循环倒流。
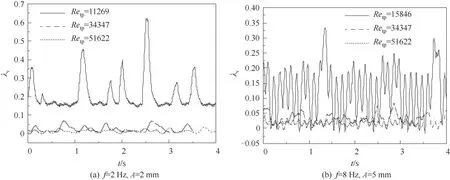
图7 不同雷诺数下的摩擦阻力系数Fig.7 Friction coefficient at different Reynolds numbers
3.4 振动参数对摩擦阻力系数的影响
3.4.1 振动幅值对摩擦阻力系数的影响 相同振动频率、雷诺数,不同振动幅值时摩擦阻力系数的波动如图8 所示。从图中可以看出,振动幅值对摩擦阻力系数的平均值和波动幅度均有明显影响。随着振动幅值从2 mm 增加至8 mm,摩擦阻力系数平均值从0.127 增至0.151,摩擦阻力系数的波动范围从-50.1%~144.4%增至-88.9%~235.1%。这是因为振动加速度和振动幅值的一次方成正比,当振动幅值改变时附加作用力变化较小,只能增大流体微团的受力而不能改变流体微团的分布情况,因此使得摩擦阻力系数的平均值和波动幅度增加。

图8 不同振动幅度下的摩擦阻力系数Fig.8 Friction coefficient under different vibration amplitude
3.4.2 振动频率对摩擦阻力系数的影响 相同振动幅值、雷诺数,不同振动频率的摩擦阻力系数的波动如图9 所示。从图中可以看出,摩擦阻力系数平均值随振动频率的增大而增大,随着振动频率从2 Hz 增加至8 Hz,平均摩擦阻力系数从0.126 变化至0.134。而振动频率对摩擦阻力系数的波动范围影响比较复杂。这是因为振动加速度和振动频率的平方成正比,随着振动频率的增大,附加作用力变化比较大,除了增大流体微团的受力外,还会改变流体微团的分布,使得摩擦阻力系数的波动变化规律比较复杂。
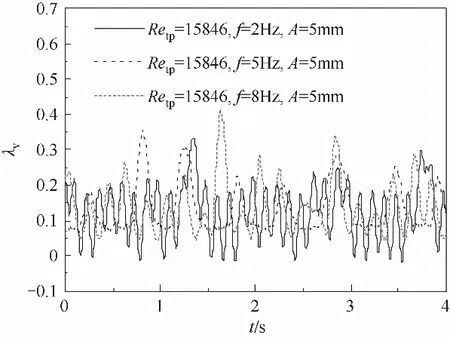
图9 不同振动频率下的摩擦阻力系数Fig.9 Friction coefficient under different vibration frequencies
3.5 倾角对摩擦阻力系数的影响
相同振动工况和雷诺数,倾角分别为10°、20°和30°的摩擦阻力系数波动如图10 所示,摩擦系数平均值分别为0.0219、0.0218 和0.0215。从图中可以看出,随倾角变化,摩擦阻力系数的波动无规律性变化。倾角由30°降至10°,摩擦阻力系数增大1.86%,这说明在30°以内倾角的改变对摩擦阻力系数的影响较小。
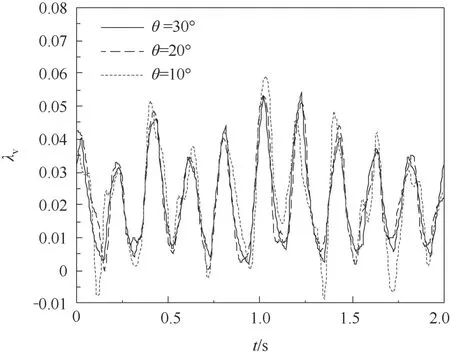
图10 不同倾角下的摩擦阻力系数Fig.10 Friction coefficient under different tilt angle
3.6 起伏振动下摩擦阻力系数计算模型
通过以上分析可得出起伏振动下摩擦阻力系数主要与起伏振动参数(a,v)和两相流动参数(Retp)有关,采用量纲分析可导出振动摩擦阻力系数的表达式。起伏振动状态下气液两相流摩擦阻力特性物理方程为:

本文得出的起伏振动状态下振动摩擦阻力系数计算值和实验值的对比如图11所示。由图可知,在峰值和谷值由于波动较剧烈,关系式误差较大,在中间位置的拟合误差较小。对实验的163组数据进行统计,计算与实验误差如图12所示。该关系式计算得到的摩擦阻力系数与实验值的平均误差为10.94%,误差在15%以内的数据组占88.34%,与现有静止管道的摩擦压降模型相比,预测准确度大幅度提升,这说明本文新建立的起伏振动状态摩擦阻力系数计算模型能够准确计算起伏振动下的摩擦阻力系数。该关系式适用于2 Hz≤f≤8 Hz、2 mm≤A≤8 mm、5166≤Retp≤83722、θ=30°、d=20 mm,且在一个振动周期内振幅和频率均保持不变的起伏振动。由于30°范围内倾角的改变对摩擦阻力系数的影响较小,该关系式对于倾斜角度在30°范围内的摩擦压降均能取得较好的预测结果。
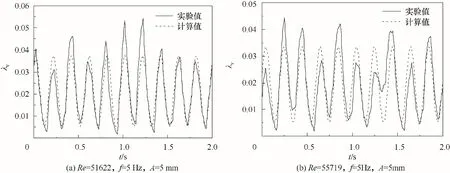
图11 振动摩擦阻力系数计算值和实验值的比较Fig.11 Comparison between calculated and experimental values of friction coefficient of vibration
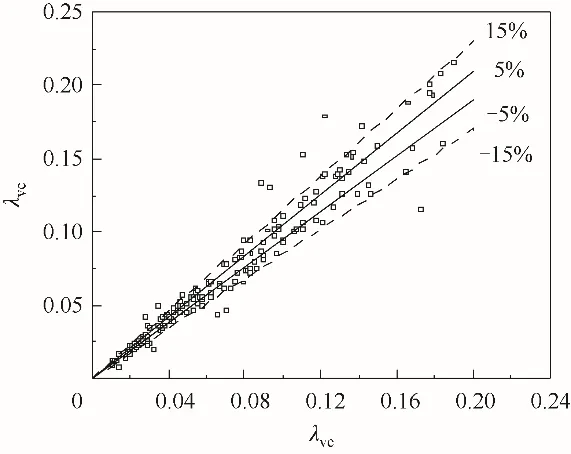
图12 新建模型计算结果误差分布Fig.12 Error distribution of new model calculation results
4 结 论
通过对起伏振动状态下不同流动和振动工况下的摩擦阻力特性进行研究,得出以下结论。
(1)与稳定状态气液两相流相比,起伏振动状态下摩擦压降平均值显著增大,除泡状流外,其他流型下摩擦压降波动熵值显著增大,且所有流型的熵值均表现大幅度振荡,流动不稳定性更加明显。
(2)起伏振动状态下的瞬时摩擦压降波动表现出明显的周期性,且波动频率与振动频率一致。
(3)起伏振动状态下,平均摩擦压降随雷诺数的增大而减小,随振动幅值和频率的增大而增大,且振动幅值对其影响比较单一,规律变化更明显。
(4)建立了起伏振动下气液两相流摩擦阻力系数计算模型,与现有静止管道的计算模型相比预测准确度大大提高。
符 号 说 明
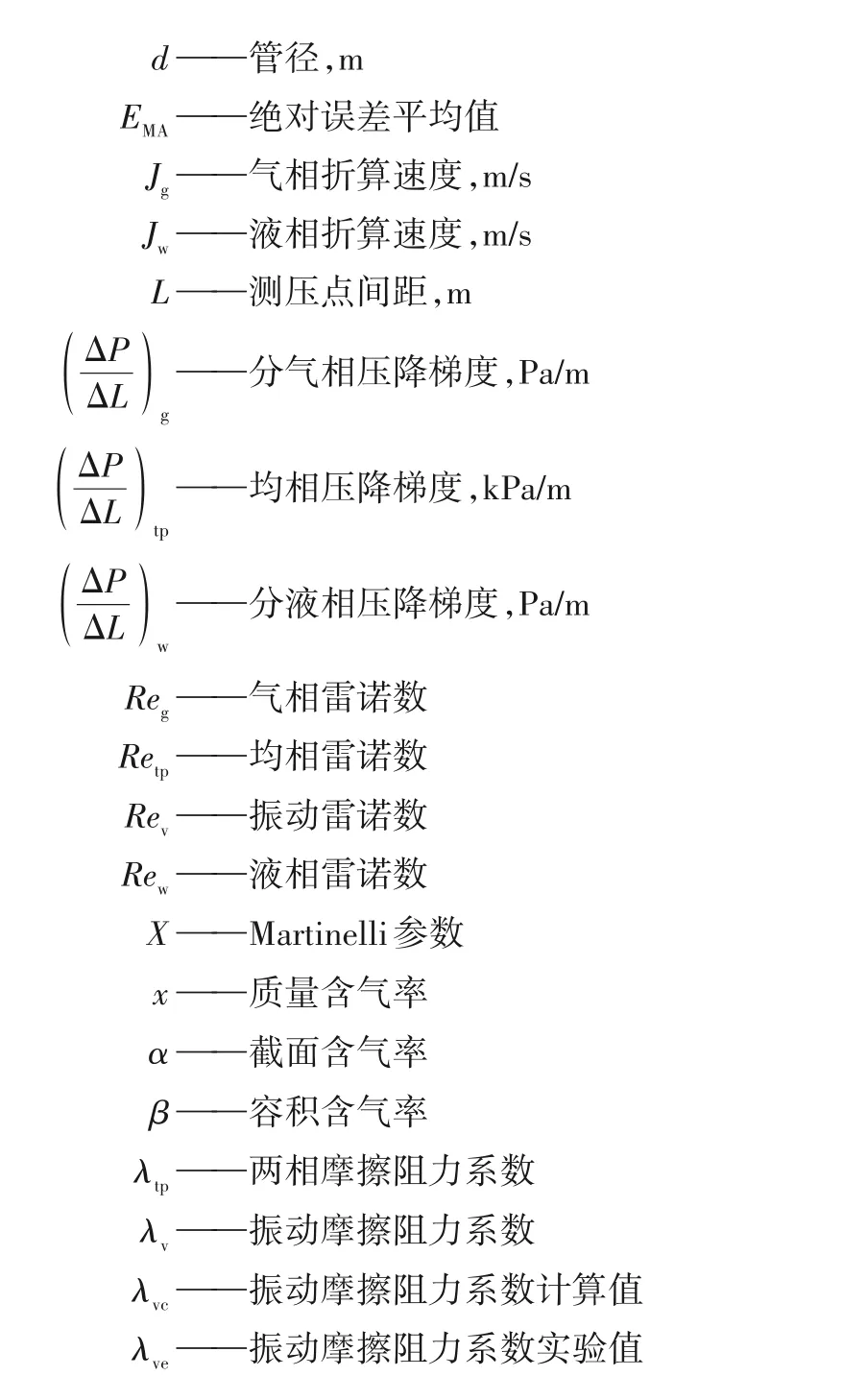
Φw——分液相折算系数
下角标
add——附加
f——摩擦
G——重位
g——气相
M——平均值
m——流动
o——真实
p——最大值
tp——均相
v——振动
vc——振动计算值
ve——振动实验值
w——液相
