双馈风电场新型功率协调控制策略研究

2022-03-03王小军段生强陈文魁阿依苏鲁艾尼瓦尔赵雁荣陈旭

湖南电力 2022年1期

王小军，段生强，陈文魁，阿依苏鲁·艾尼瓦尔，赵雁荣，陈旭

(国网新疆克州供电公司，新疆克孜勒苏柯尔克孜自治州845350)

0 引言

随着国家对新能源的逐渐重视，风力发电成为新能源发电最为成熟的方式之一，每年风力发电装机容量也随之不断增加，但大规模的风电并网所造成的电能质量问题也越来越多，其中风电场并网点的无功电压问题就是最为突出的问题之一[1－2]。在现今的风电场中双馈异步风力发电机组(DFIG)通常不考虑利用自身的无功调节能力，以恒功率因数方式运行，采用一些无功补偿设备对风电场所需无功进行补偿，但这就忽略了DFIG这一优质无功源，提高了风电场的运行成本[3－4]。

文献[5]通过分析输电线路参数对风电系统的影响及发生故障时二次跳机的原因，提出基于LC、SVC与双馈风电机组的无功协调方法。文献[6]阐述了在电网发生短路问题而引起撬棒保护投入运行时，针对双馈风机RSC、GSC与STATCOM之间的协调控制进行了研究。文献[7]开展了调相机与STATCOM的无功支撑能力论证，STATCOM在动态无功与短路电流协同控制方面具有独到优势。文献[8]通过对多种无功补偿装置的比较，选用TCR＋FC型的协同SVC系统进行无功补偿。文献[9]提出了一套以风电机组无功输出为主、SVG无功输出为辅的AVC协同系统优化控制方法抑制谐波。文献[10]在双馈风电场中加入静止同步补偿器(STATCOM)，用以补偿Crowbar动作后DFIG异步运行时对电网的无功需求。本文将通过无功功率分频的角度来协调控制DFIG与STATCOM的无功出力。

1 DFIG与STATCOM的控制模型

双馈风力发电机控制结构包括转子侧变换器(Rotor Side Converter，RSC)与网侧变换器(Grid Side Converter，GSC)，为了使变换器直流侧电压保持稳定，让GSC运行在恒功率模式下，文中不再介绍其控制结构。

RSC与STATCOM调节特性都为连续平滑动态调节，产生感、容性无功，但在响应时间上RSC是秒级，而STATCOM是毫秒级。RSC在响应时间内对应的频率响应范围在0～17 Hz，而STATCOM响应迅速可对应全频段[11]。故可把系统所需无功功率信号频段的0～17 Hz定义为低频段，作为RSC控制策略中的无功参考功率，高于17 Hz的频段定义为高频段，作为STATCOM控制器中的无功参考功率。

1.1 DFIG控制结构

RSC的控制策略采用基于定子磁链定向的DFIG矢量控制策略，即功率外环、电流内环的双闭环控制系统。在功率外环控制中，P*可以根据风力机捕获最大风能的原则给出[12]。利用CEEMD分解算法对求得的并网点所需瞬时无功功率进行分频、重构，得到的低频段即为RSC控制策略中的无功功率参考值Qs*[13]。反馈功率P、Q则是通过检测双馈发电机定子输出电压、电流并进行派克坐标变换后经计算求得。

转子电压的d、q轴分量可由下式求得:式中，irq、ird分别为转子电流的转矩电流分量和励磁电流分量，ωr为转子角频率，Ls、Lr分别为定、转子自感，Lm为定、转子互感，ψsd为定子磁链的d轴分量。

1.2 STATCOM控制结构

STATCOM控制结构如图1所示，其控制策略和RSC的控制策略相近，都采用双闭环控制。由CEEMD算法对系统所需无功调节量进行分频、重构得到的那个高频段即为STATCOM无功功率参考值，直流侧电压参考值为，经双闭环、坐标系反变换控制PWM产生触发信号作用于STATCOM。

图1 STATCOM控制框图

2 基于CEEMD的无功功率分配

对双馈风电场并网点求出的系统所需无功调节量进行分频，本质上就是利用一些智能算法对其进行滤波处理[14－15]，采用CEEMD来分解、重构无功功率信号。CEEMD分解算法相比经验模态分解算法(EMD)具有很大的优势，例如不存在模态混叠和边界效应等问题，同时CEEMD可通过增加正负白噪声能够完全消除白噪声对重构信号的影响。

原始无功功率具体分解过程如下:

1)对原始无功功率信号qw(t)中加入正负白噪声(－1)va0ni(t)后对信号进行一次EMD分解:

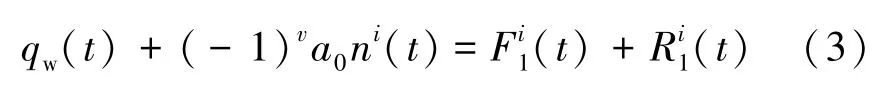
式中，v＝1，2；i＝1，2，……M/2，其中M/2是原始无功功率加入的正负白噪声对数；是无功功率剩余分量，对M个固有模态分量(IMF)F1i(t)求其平均值得到第一个固有模态分量:

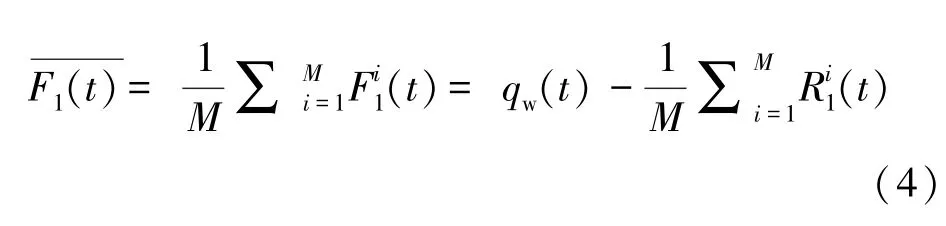
式(4)中完成M次集合平均后噪声对相互抵消，模态分量中不存在白噪声信号。

2)提取第一个模态分量并得到剩余无功功率分量:

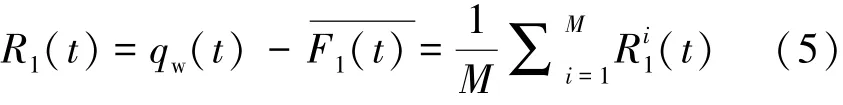
对剩余无功功率加入经EMD分解的噪声分量，进行EMD分解:

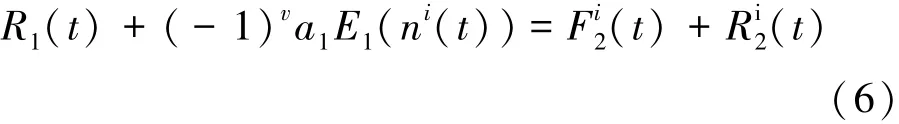
对上式M个固有模态分量F2i(t)结合平均后得到第二个固有模态分量:

无功功率剩余分量为:

3)循环步骤2)，直到提取原始无功功率中所有固有模态分量。

4)经CEEMD分解后重构信号qw(t)可表示为:

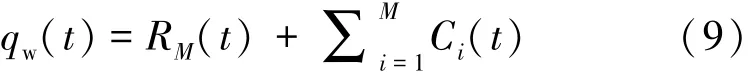
式中，RM(t)为残余信号，Ci(t)为第i(i＝0，1，2……n)层固有模态函数，并以频率由高到低依次分布。然后将IMF分量通过滤波器重构得到低频段和高频段，分别作为DFIG和STATCOM的参考功率。

低频段为:

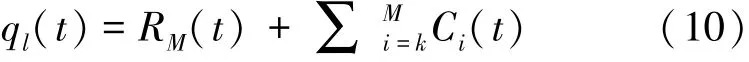
式中，k为滤波器的滤波阶数。

高频段为:

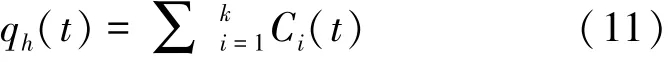
3 DFIG与STATCOM的功率协调控制策略

DFIG和STATCOM的功率协调控制如图2所示。

图2 无功功率协调控制框图

DFIG转子侧无功容量Qsmax可由公式(12)求得:

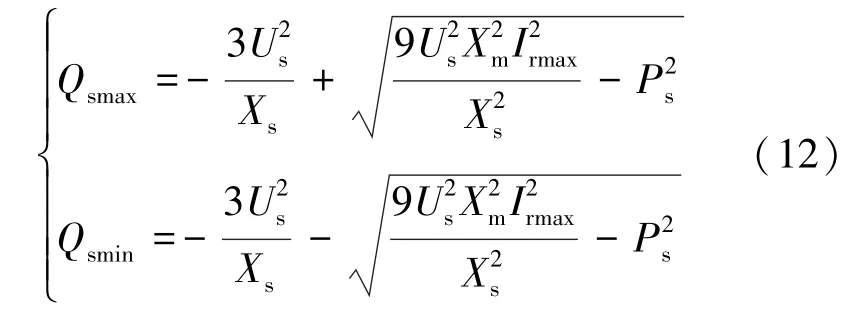
式中，Xm、Xs分别为激磁电抗和定子漏抗，Us、Ps分别为转子电压有效值和定子侧有功功率，Irmax为最大转子电流。

风电场并网点所需的无功调节量ΔQ可由公式(13)求出:

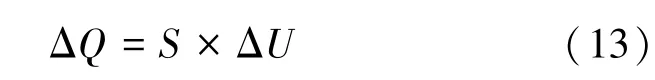
式中，S为并网点无功功率关于电压灵敏度，ΔU为实时测得的风电场并网点电压偏差。设节点A的无功变化量为∂Q，节点B的电压变化量为∂V，那么点A对点B的电压灵敏度SBA可由下式确定:

然后在满足RSC无功容量的前提下利用互补式经验模态分解算法对所求得的双馈风电场并网点无功功率调节量ΔQ进行分频、重构得到高频段分别作为RSC和STATCOM控制器的触发信号，控制二者对风电场无功功率的变化作出快速响应。

4 仿真分析

利用Matlab/Simulink模拟了某地区DFIG风电场，该风电场共由33台1.5 MW的DFIG组成。总的装机量共有49.5 MW，机组出口电压为690 V，机组通过变压器T1升压到35 kV，静止同步补偿器STATCOM接在并网点B35，容量为5 Mvar，在经10 km线路由T2升压到110 kV，最后接入大电网，相关风机控制参数见表1。本文针对风速连续变化、短路故障两种情形进行验证。

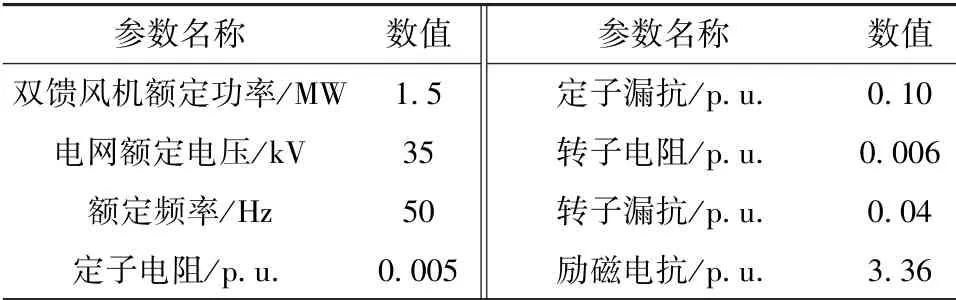
表1 风电系统仿真控制参数

4.1 风速连续变化仿真

风电场模拟仿真结果如图3所示。图3(a)为该仿真系统所选取的风速模型，图3(b)为该功率协调控制策略下的风电场并网点电压，图3(c)为DFIG和STATCOM的无功出力。

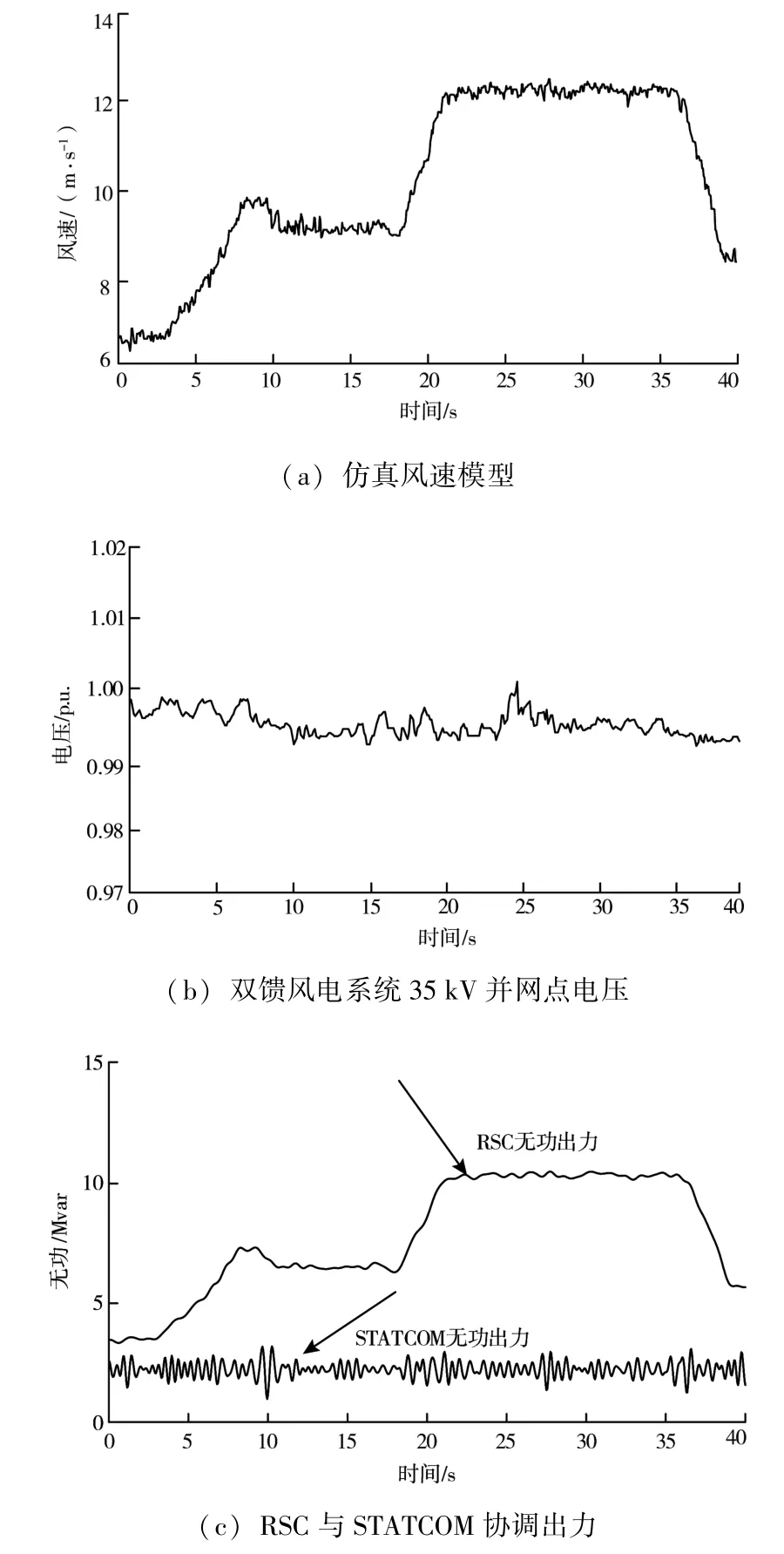
图3 风速变化下功率协调控制

从图3(b)中可以看出，在所选择的风速模型下，采用所提功率协调控制风电系统35 kV并点电压的最大值仅为1.002 p.u.，最小值为0.995 p.u.，经计算电压波动率仅为7%，满足风电并网要求。从图3(c)中可以看出，DFIG和STATCOM的无功出力，二者在两个频段内共同对系统所需无功功率调节量进行补偿，充分利用了DFIG的无功调节能力，提高了DFIG风电场运行的经济性。

4.2 短路故障仿真

为验证所提功率协调控制策略在短路故障下的优势，采取以下两种方式进行仿真，分别为采用所提控制方法和仅采用DFIG的转子侧换流器对风电场所需无功进行补偿。设定风速为8 m/s，控制目标是维持母线B35电压为1.0 p.u.，在时间为0.7 s时发生三相短路故障，电压跌落幅值为0.8 p.u.，1.0 s后故障恢复，如图4所示。

图4 短路故障下功率协调控制

从图4中可以看出，当电压幅值跌落为0.8 p.u.时，仅采用双馈风电机组自身的无功补偿能力进行补偿可以把风电场并网点电压升到0.89 p.u.，而采用基于DFIG与STATCOM的功率协调控制策略可以把并网点电压升到0.94 p.u.，而且在该策略下，短路故障切除后，能够抑制电压振荡，使并网点电压更快地恢复至稳定状态。