低雷诺数下襟翼缝隙几何参数对双元素翼帆推进特性的影响研究
2022-03-03孙培廷
李 臣,孙培廷
(1.大连海事大学轮机工程学院,辽宁大连 116026;2.江苏海事职业技术学院轮机电气与智能工程学院,南京 211170;3.江苏船舶节能减排工程技术研究开发中心,南京 211170)
0 引 言
双元素翼帆作为一种船舶辅助推进装置,在无动力帆船领域得到快速的发展。然而,由于翼帆表面存在流动分离或失速现象,翼帆的推进性能将发生恶化,严重影响着船舶的稳性。为了改善风帆的失速特性,人们采用了多种不同的流量控制方法,流量控制可分为主动控制和被动控制。在翼帆的后缘设置襟翼是一种控制流动分离的主动控制方法,通过翼帆主翼和襟翼之间的缝隙来控制帆在左右两弦的弧度,以提升推进性能,延迟失速发生,因此襟翼缝隙参数的设置对翼帆的流动分离或失速控制具有重要的意义,许多学者也对此开展了气动特性研究。
1996年,Daniel[1]设计了一种高性能三元素翼帆,通过控制缝隙宽度和襟翼偏转角等参数,发现三元素翼帆的最大推力系数可提高28%,失速发生角可推迟4°~6°,整个操作区域的翼帆推力也增加了,这证明了缝隙参数对于多元素翼帆在推进性能提升方面的重要作用。2015 年Fujiwara 等[2-3]与Li 等[4]合作对混合式帆的主翼进行改型,用刚性平板代替襟翼,取消缝隙,用双回转桅杆分别控制主翼和平板转动,以改变风帆的拱角,因此这种帆也被称为可变拱角帆(VCS)。经仿真和试验验证,该帆的综合推进性能优于NACA 0021 帆和平板帆。Blakeley 等[5]对“美洲杯”AC45 双体船的多元素翼帆的推进特性进行试验研究,认为增加襟翼后,保持襟翼折转角不变,随着缝隙宽度的减小,风翼的失速角推迟。Chapin等[6]开展了双元素翼帆的仿真研究,认为由于层流分离气泡的存在以及主翼和襟翼边界层在缝隙区域的相互作用,襟翼边界层产生了过渡现象,风翼失速与发生非线性耦合的缝隙泄漏流有关,而缝隙泄露流的变化规律受襟翼偏转、缝隙宽度和襟翼厚度等参数的多重作用。这说明多元素翼帆具有复杂的气动特性,需要对其失速行为进行更深入的研究。Fiumara 等[7]通过PIV 测量和数值模拟,详细解释刚性翼帆在低和高襟翼偏转角下的流动现象,提出缝隙内流场是影响翼帆性能的关键因素,然而对缝隙几何尺寸变化与翼帆空气特性的发展规律的内在关系研究尚不明确。
为了更好地了解双元素翼帆缝隙对其气动特性的影响规律和发生机理,本文通过在定常和非定常工况下借助雷诺平均N-S 方程研究翼帆缝隙参数(襟翼偏转角、缝隙相对宽度等)对双元素翼帆推进特性的影响,并分析规律背后的作用机理,为双元素翼帆的设计提供参考依据。
1 物理模型与数值方法
1.1 翼帆模型设计方案
双元素翼帆的主翼和襟翼的弦长比c1/c2=1.5,其他参数设置如图1 所示,名称定义为t1815Xr85g2.4δ15。其中,t1815代表主翼厚度e1/c1=18%,襟翼厚度e2/c2=15%,Xr85 代表襟翼旋转轴位于主翼弦长的85%位置,g2.4 代表缝隙相对宽度g/c1=2.4%,δ15 代表襟翼偏转角为15°。为简化物理模型,双元素翼帆参数变量设置如表1 所示。图2为双元素翼帆的三维模型图。
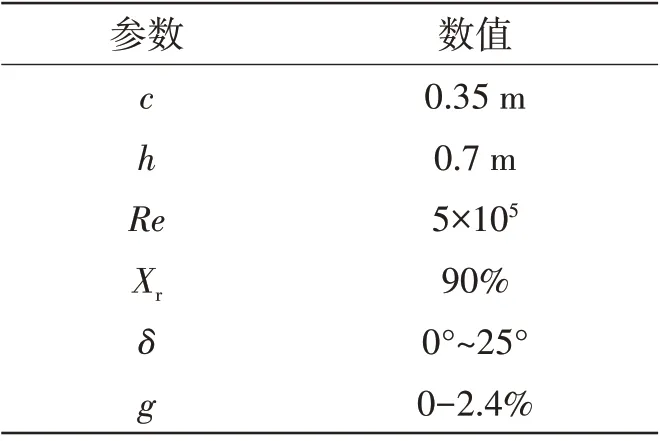
表1 翼帆配置方案Tab.1 Parameters of wingsail

图1 双元素翼帆的参数定义图Fig.1 Wingsail geometry definition
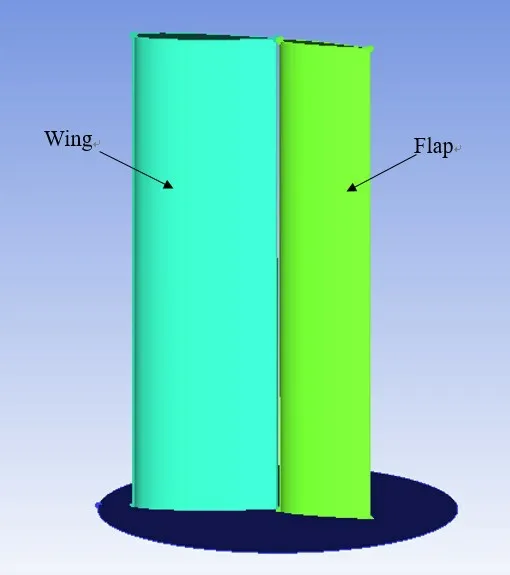
图2 双元素翼帆的三维模型Fig.2 Three dimensional model of two-element wingsail
1.2 计算域和边界条件
数值仿真时为了避免边界对双元素翼帆外流场的影响,必须保证其计算域足够大。考虑到本文讨论的静水状态下双元素翼帆的空气动力特性,且不研究船体表面边界层对翼帆展向流场的影响,为减小计算时间,本文将模型计算域简化处理,如图3 所示,船面与计算域底面重合,将计算域底面与翼帆表面的边界条件设置为无滑移边界条件,计算域底面边界层暂不考虑。翼帆前缘到计算域进口的距离为12c,翼帆尾缘到计算域出口的距离是20c,翼帆表面到迎风面和被风面的距离都是15c。计算域的进口边界条件设置为速度入口,在三个边界(入口面、背风面、迎风面)均匀流入,速度大小与自由流速度相同,速度方向根据攻角调整x、y轴比例;出口边界条件设置为压力出口,压力大小等于远场压力[8]。
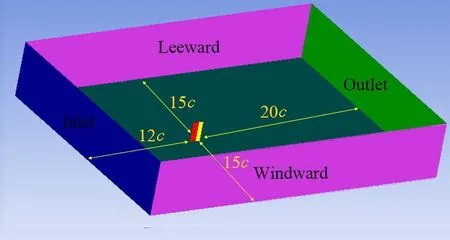
图3 计算域Fig.3 Calculation domain
1.3 网格划分和收敛性研究
本文计算域模型采用非结构化网格,为了精确地模拟出主翼尾流、缝隙射流和襟翼边界层之间相互作用区域的流动情况,对间隙网格和壁面网格进行了加密处理(如图4),间隙网格大小设置为0.4545%c(如果网格数为986 万)。为精确模拟双元素翼帆附面层流动的细节,需计算边界层第一层网格到翼帆壁面的距离值,如公式(1)所示。
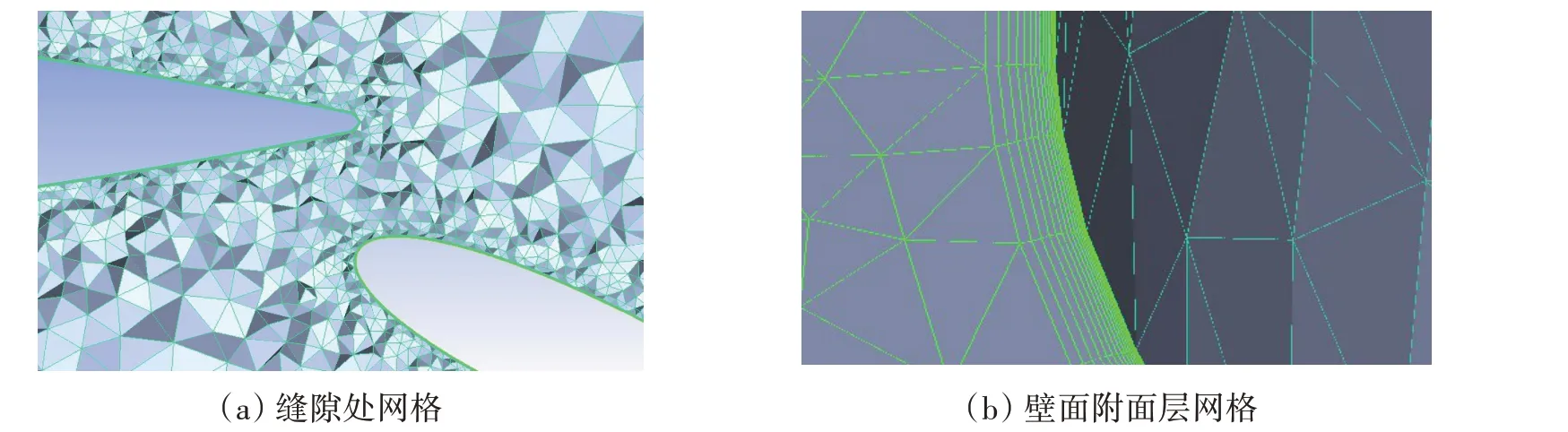
图4 加密的网格Fig.4 Encrypted mesh
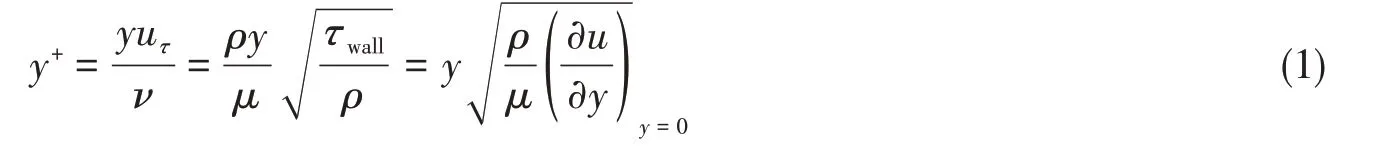
式中,y为边界层第一层网格到翼帆壁面的距离,uτ为壁面的摩擦系数,ν为空气的运动粘度,ρ为空气的密度,μ为动力粘度,τwall为壁面剪切力。为保证y+值小于等于1(如图5),y值求得为2.871×10-5c,附面层网格层数的密度为1.2,网格总数约为986万。

图5 攻角为8°时翼帆壁面的y+值Fig.5 Wall y+contour on wingsail surface(α=8°)
为了保证网格数量对数值计算结果不产生影响,在雷诺数Re=5×105时,用四种不同的网格数(包括422万、634万、986万和1440万)估算网格收敛性。在襟翼偏转角为15°时,攻角α=8°的定常工况下和α=20°的非定常工况下进行网格无关性分析。对于非定常工况,为保证库朗数CFL=VΔt/Δx=1,时间步长被设定为1.6×10-4s。图6为双元素翼帆模型的升力系数和阻力系数在α=8°和α=20°的收敛结果。如图所示,当网格数增大至986万时,升力系数有很小的变化,其误差在986万时和1440万时之间,小于0.2%,这认为是可接受的。

图6 攻角在8°和20°时网格数的收敛性Fig.6 Convergence at α=8°and α=20°as a function of mesh number
为了进一步验证网格可靠性,还分析了Re=5×105在α=20°时网格尺寸对流场的影响,对于四种不同的网格(包括422 万、634 万、986万和1440万),x-y平面上的速度矢量如图7所示。可以观察到,在吸力面上有一个大的分离涡,在尾流有一个小的涡,分别由986万和1440万的网格产生,而对于422万和634万的网格没有明显的流动分离。在986万和1440万网格之间,翼帆流场没有显著差异。因此,986万的网格数适合于研究翼帆。
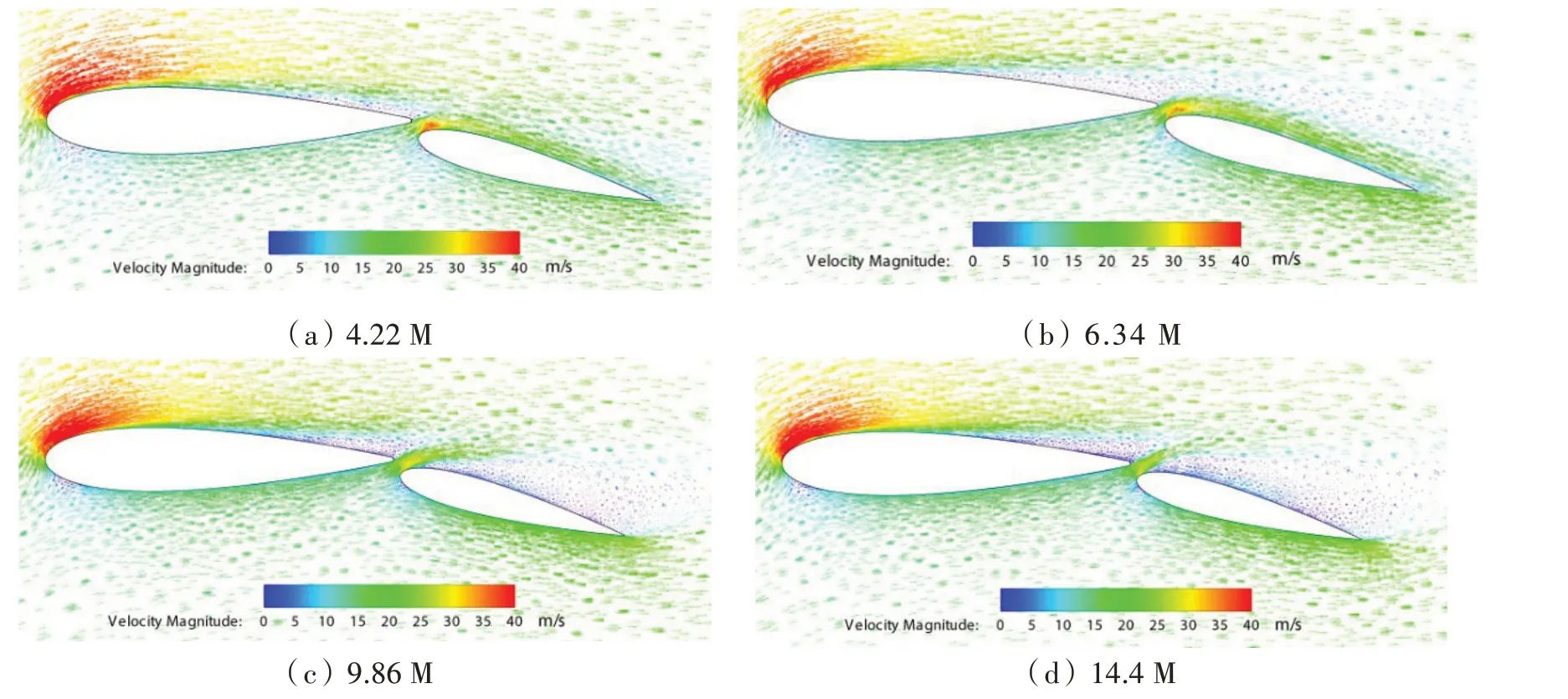
图7 翼帆中截面的速度矢量图Fig.7 Flow profiles on the mid-span of wingsail
1.4 数值方法与模型验证
为了准确模拟双元素翼帆的流场变化情况,采用雷诺平均N-S 方程组对翼帆计算域模型进行数值仿真,湍流模型为k-ωSST模型[9],进口湍流密度设为1%,离散格式采用quick格式,压力-速度耦合格式采用simple算法[10]。对于非定常雷诺平均N-S方程,时间步骤被设定为1.6×10-4s。
为了确保数值模拟的可信度,将NACA 0018 翼型在自由流环境下的升力和阻力系数与实验结果[11-12]进行比较,如图8所示。在Re=3.2×105的情况下,对RANS方法进行了数值验证。在失速发生前(α<15°)升力系数与阻力系数的数值计算结果与实验值接近,估计误差小于3%,且失速发生位置预测比较准确,失速发生后,数值预测结果与实验值有所差别,这是由于数值仿真不能精确模拟翼帆外流场的微小涡流引起的流动损失。这不影响本文在数值计算中对双元素翼帆升阻特性的定性研究以及对失速流场大尺度流动变化的模拟,因此数值方法适合于翼帆的研究。
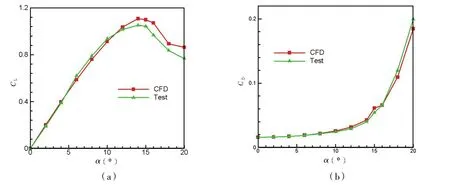
图8 实验和数值仿真的升力系数和阻力系数对比分析Fig.8 Comparison of lift coefficient and drag coefficient between test and CFD results
2 结果分析
2.1 双元素翼帆的性能分析
升力系数和阻力系数是衡量翼帆推进性能重要的无量纲参数。为了定量地描述翼帆的升阻特性,本文定义的升力系数CL和阻力系数CD如下所示:

式中,FL和FD分别为翼帆的升力和阻力,VR是计算域入口速度大小,AR是翼帆的表面积。
为了研究缝隙相对宽度和襟翼偏转角对双元素翼帆性能的影响规律,选择缝隙相对宽度分别为1.2%、2.4%和3.6%,改变襟翼偏转角(δ=5°、10°、15°,20°,25°),计算结果如图9所示。
从图9(a)中可以看出,缝隙相对宽度g=1.2%时,在失速发生前升力系数基本随襟翼偏转角的增加而增加,失速角减小,最大升力系数在襟翼偏转角为25°、攻角为10°时产生,其值为2.49。而图9(b)中升力系数随襟翼偏转角变化的规律发生改变,双元素翼帆的最大升力系数随襟翼偏转角的增加先增加后减小,在襟翼偏转角为10°、攻角为13°时最大,其值为3.14。图9(c)中的最大升力系数下降较快,攻角在6°~16°时,不同的襟翼偏转角对应的翼帆基本都在发生失速。从图9 的对比中可以看出,在不同的缝隙相对宽度中,双元素翼帆的最大升力系数随襟翼偏转角变化的规律发生改变,且最大升力系数随相对缝隙宽度的增加先增大后减小,其最大值产生在缝隙相对宽度g=2.4%,襟翼偏转角为10°、攻角为13°时,可见缝隙相对宽度对最大升力系数大小的影响要大于襟翼偏转角。因此,在选择最大升力系数时,需先考虑缝隙相对宽度因素,再考虑襟翼偏转角。
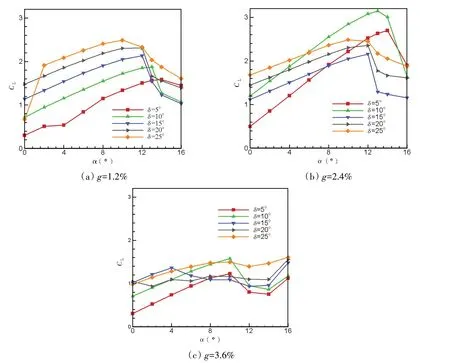
图9 三种缝隙相对宽度时不同襟翼偏转角下升力系数随攻角的变化曲线Fig.9 Lift coefficient versus angle of attack with three relative widths of the slot
2.2 流场性能分析
2.2.1 失速形成机理分析
为了清晰地分析不同攻角时的速度分布情况,首先研究了缝隙相对宽度为2.4%、襟翼偏转角为10°,攻角在6°、10°、13°、15°时,双元素翼帆在中截面的速度分布,如图10所示。
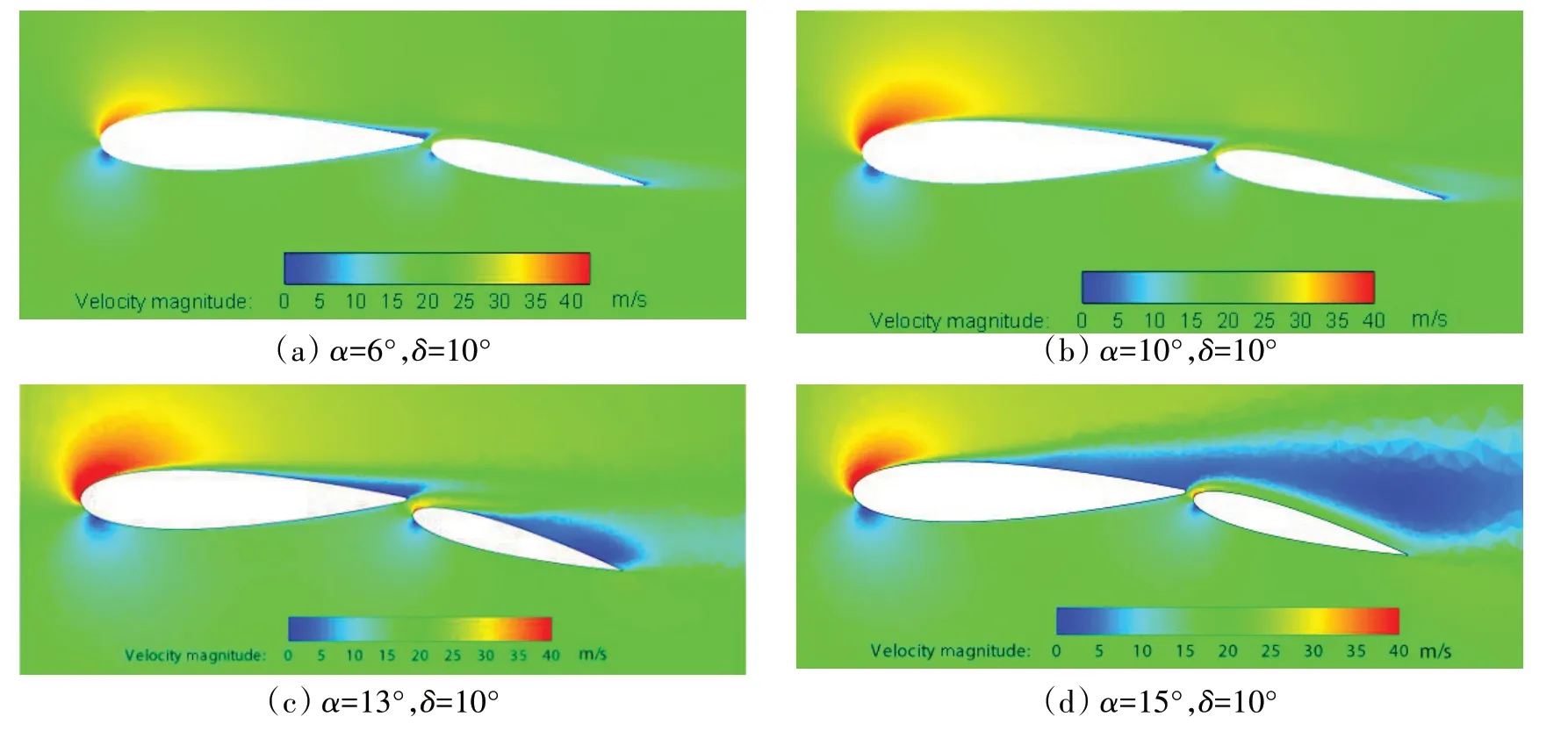
图10 g=2.4%时翼帆中截面的速度云图Fig.10 Velocity magnitude contours at mid-span with g=2.4%
从图10 中可以发现,在失速发生前(α=6°和10°),双元素翼帆的速度分布比较均匀,主翼尾流的低压区由于狭缝射流的能量补充没有发生流动分离,流场形态结构完好,因此可产生稳定的升力。随着攻角的增大,主翼吸力面的层流分离点前移,这促使主翼尾流的能量损失扩大,在最大失速角(α=13°)由于狭缝射流的流体能量及时补充没有发生失速现象,而此时的主翼进口压力面和吸力面的巨大压差提升了升力。失速发生后(α=15°),由于攻角过大,主翼吸力面的层流完全分离,狭缝射流仅仅沿襟翼吸力面附面层流动,对主翼尾流的能量补偿不足,流过双元素翼帆的流体可能会产生周期性的旋涡脱落现象,这时的双元素翼帆升力会产生波动。
为了更深刻地理解失速发生后双元素翼帆尾流的旋涡脱落规律和特点,现对缝隙相对宽度为2.4%、襟翼偏转角为15°,攻角在15°时的非定常流动进行数值分析,如图11所示。从图中可以清楚地看到,一个波动周期内双元素翼帆吸力面流动分离的变化情况。在主翼尾流的旋涡影响下襟翼吸力面的层流逐渐分离,由螺旋分离点发展成明显的旋涡结构,这是双元素翼帆升力出现周期性波动的主要原因。

图11 在g=2.4%,δ=15°,α=15°时翼帆中截面的流线分布Fig.11 Streamlines with mid-span of wingsail at g=2.4%,δ=15°,α=15°
2.2.2 不同襟翼偏转角时的流场分布
为了研究不同襟翼偏转角时的流场分布情况,本节分析了不同襟翼偏转角时双元素翼帆吸力面的静压和极限流线分布,如图12所示。从图中可以看出,随着襟翼偏转角的增大,主翼吸力面的角区分离从叶根部向叶顶扩展,回流面积越来越大,在襟翼偏转角为15°时,主翼吸力面出现了一条明显的流动分离线,这说明襟翼偏转角的增大加速了主翼和襟翼吸力面的流动分离,降低了双元素翼帆的最大升力系数。因此,襟翼偏转角的选择需首先保证缝隙射流能足够补充主翼尾流因边界层分离引起的能量损失。
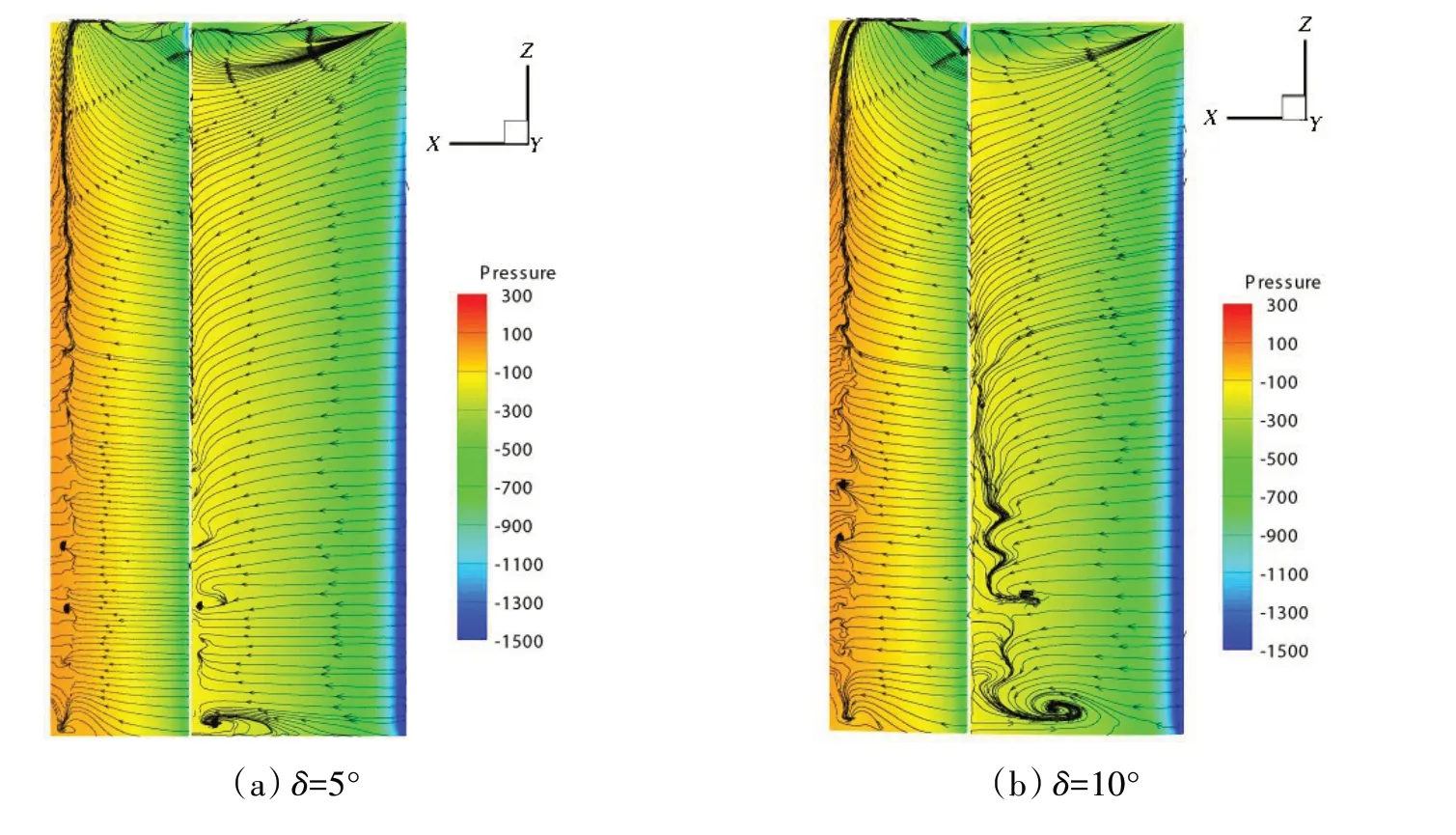
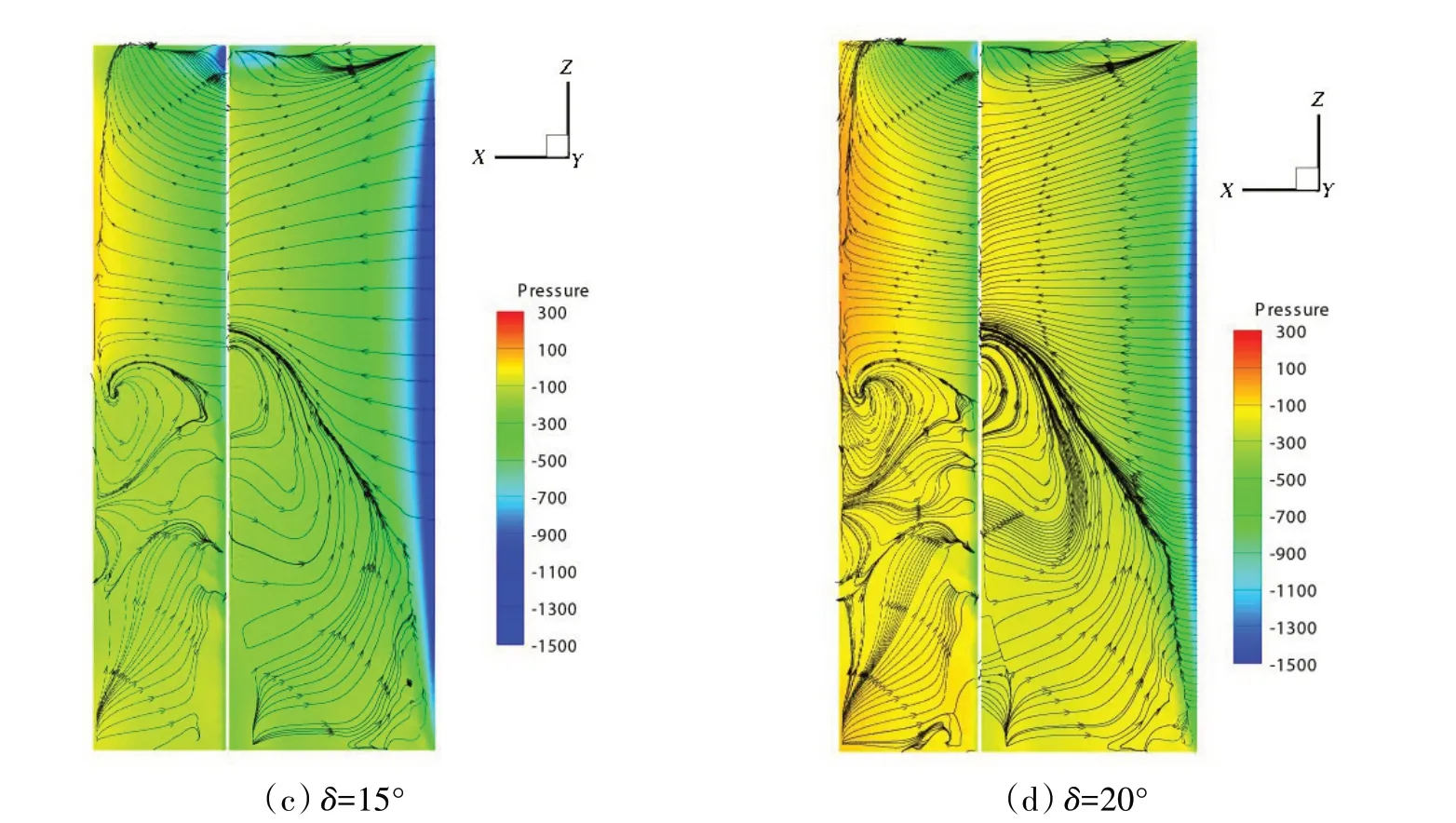
图12 在g=2.4%,α=13°时双元素翼帆吸力面的静压云图和极限流线Fig.12 Limiting streamline and static pressure contours on suction surface of two-element wingsail at g=2.4%,α=13°
为了比较失速前后不同襟翼偏转角时翼帆的压力载荷分布情况,本文分析了g=2.4%时双元素翼帆中截面的压力载荷分布,如图13 所示。在失速发生前(α=6°),主翼的压力载荷分布受襟翼偏转角的影响较小,而由于偏转角的不同,襟翼吸力面压力载荷变化较大,襟翼偏转角增大时吸力面尾缘的压力下降较大;而失速发生后(α=15°),随襟翼偏转角的增大,主翼前缘的最低压力升高较多,襟翼的吸力面由于流动分离引起压力载荷的波动。
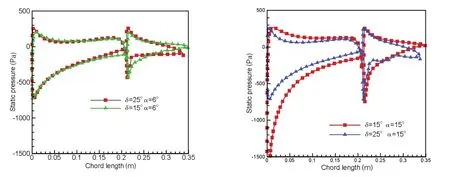
图13 g=2.4%时翼帆中截面的压力载荷分布Fig.13 Pressure load distribution at mid-span with g=2.4%
2.2.3 不同缝隙相对宽度时的流场分布
为了研究不同缝隙相对宽度时的流场分布情况,本节分析了襟翼偏转角为15°,攻角为6°,缝隙相对宽度为1.2%、2.4%和3.6%时双元素翼帆中截面的速度矢量分布,如图14 所示。从图中可以看出,在α=6°,g=1.2%和2.4%时,双元素翼帆吸力面的流体速度分布结构完好,流动尚未发生分离,而随着相对缝隙宽度的增加,主翼尾流和襟翼吸力面出现了低速区且发生了回流现象,因此缝隙宽度不宜过大。图15 显示了失速后双元素翼帆中截面的速度矢量分布情况,从图中可以看出,g=1.2%、2.4%和3.6%时,双元素翼帆吸力面均出现不同程度的低速回流现象,而g=1.2%时由于缝隙相对宽度过小导致绕流主翼尾缘的流体较少,主翼尾流没有产生低速旋涡,失速后的升力下降较快而波动较小。随着缝隙相对宽度的增加,主翼吸力面产生旋涡并不断减小,这是由于流过缝隙的流体回流到主翼尾流旋涡而造成的,有助于提升双元素翼帆的升力。
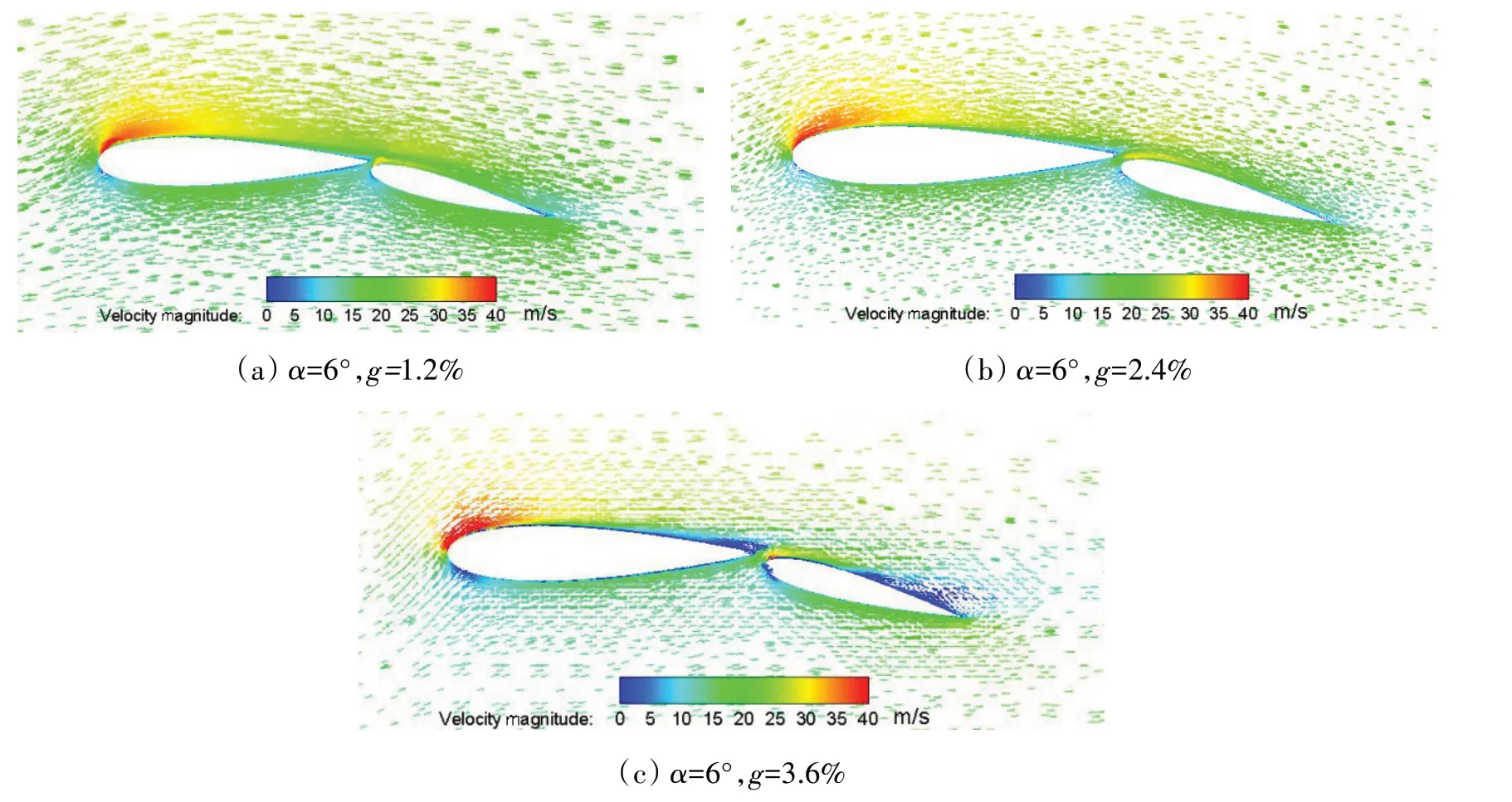
图14 δ=15°,α=6°时双元素翼帆中截面的速度矢量云图Fig.14 Flow profiles on the mid-span of the two-element wingsail at δ=15°and α=6°
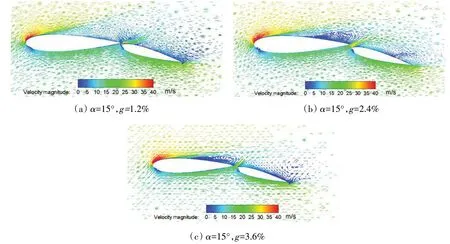
图15 δ=15°,α=15°时双元素翼帆中截面的速度矢量云图Fig.15 Flow profiles on the mid-span of the two-element wingsail at δ=15°and α=15°
3 结 论
本文针对双元素翼帆模型,对不同襟翼偏转角及不同缝隙相对宽度时翼帆的气动特性和失速规律进行了CFD 数值模拟研究,重点分析了失速前后不同襟翼偏转角时双元素翼帆的升力系数和流场变化,得出以下结论:
(1)对于双元素翼帆,当攻角大于失速角时,在主翼尾流的旋涡结构影响下襟翼吸力面的层流也逐渐分离,由螺旋分离点发展成明显的旋涡结构,这是双元素翼帆升力出现周期性波动的主要原因。
(2)增大双元素翼帆的襟翼偏转角时,最大失速角会减小,而最大升力系数同时受到缝隙相对宽度的影响,随缝隙相对宽度的增加先增大后减小,且缝隙相对宽度对最大升力系数大小和速度流场的影响要大于襟翼偏转角,襟翼偏转角的选择需首先保证缝隙射流能足够补充主翼尾流因边界层分离引起的能量损失。
(3)增加双元素翼帆的缝隙相对宽度时,主翼尾流和襟翼吸力面先后出现了低速及回流现象,而缝隙相对宽度过小时绕流主翼尾缘的流体会减少,最大升力系数较低,因此缝隙相对宽度和襟翼偏转角共同影响着双元素翼帆的气动特性。
