分层流体中自航和拖曳模型生成内波特性实验

王宏伟，盛 立，傅江妍

（1.中国舰船研究设计中心，上海 201108；2.中国人民解放军 92578部队，北京 100161）

0 引 言

潜艇的隐身和探测在大国军事角逐中至关重要。近年来，随着非声探测技术的快速发展，一些军事强国逐渐将探潜和反潜手段聚焦到潜艇尾迹等非声探测上。在密度分层海洋中，潜艇运动会激发海洋内部波动，即内波。这一内波在传播演化过程中有可能会引起海洋表面的辐聚辐散效应，进而改变合成孔径雷达（SAR）的后向散射特性，并在SAR 影像中留下其踪迹[1]。因此，对水下航行体内波的研究，既具有学术意义，还具有潜在的军事应用价值，但其中的关键还是水下航行体内波生成机理及其表现特征问题[2]。

一般研究中，将潜艇简化为球体或细长回转体，采用拖曳的方法进行研究。结果表明，在密度分层流体中拖曳物体产生的内波可分为两类[3-5]：一类是由运动物体排水效应诱发产生的内波，称为体积效应内波；另一类是由运动物体尾迹塌陷以及尾迹中各种不稳定结构诱发产生的内波，称为尾迹效应内波。

定义内Froude数（internal Froude number）为Fr=U/(DNmax)，其中U为物体运动速度，Nmax为密度分层流体的最大浮力频率（后文将阐述其定义），D为物体的特征直径。针对球体的实验研究发现[6-10]：当Fr＜2时，内波主要表现为体积效应内波；当Fr＞2时，内波又以尾迹效应内波为主。而针对细长体及回转体的研究也表明[11-16]，存在一个与物体长径比近似为线性关系的临界内Froude数Frc，界定了两类内波的占优区间。

体积效应内波的激发源包括物体本身及其回流区产生的排水效应，这类内波的相关速度与拖曳速度一致。体积效应内波相对于物体的运动是定常的，在理论上可采用移动点源或偶极子等来模拟物体的体积效应，将其作为源项加入线性化的连续性方程中，然后采用驻相法、射线法和远场积分法等方法进行求解。采用这种简化理论方法，可以获得体积效应内波模态结构、波系特征及等相位面等清晰的物理图案[15-22]。

尾迹效应内波的形成机理较为复杂，包括近尾迹、尾迹塌陷及晚尾迹激励等因素。这类内波的相关速度与拖曳速度无关，其相对于物体的运动是非定常的。在密度分层流体中，拖曳物体的近尾迹存在类似于均匀流体中的各种不稳定结构[23]，其中K-H 不稳定性是产生尾迹内波的主要因素之一[24]。当近尾迹在达到一定高度后，受浮力的抑制作用发生塌陷，进而产生塌陷内波，并以射线形式向外传播[25-26]。晚尾迹是一类大尺度湍流相干涡结构[27-28]，其主要表现特征是垂向厚度相对较簿而水平空间相对特别大的饼状涡街结构。Bonneton等[8]的实验结果显示，晚尾迹边界的周期性涡环溃破是诱发内波的因素之一，而Robey[9]和王进等[12-13]的实验结果则显示晚尾迹中大尺度相干涡与密度分层流体的共振作用是激发大振幅随机内波的主要因素之一。Robey[9]将大尺度相干结构等效为一个移动柱型质量源，建立了尾迹内波的一个简化理论预测模型，而尤云祥等[29]将大尺度相干涡结构等效为一个轴对称回转体型质量源，对该理论模型进行了改进，结果表明，改进的理论模型可以更好地预测尾迹效应内波的峰-峰幅值特性。Wang等[15]提出了针对不同长径比拖曳体产生尾迹效应内波激发源的统一理论模型。陈科等[16]提出了尾迹效应内波正对称和反对称组合激发源的统一理论模型。

基于拖曳体的内波研究已经取得了很多有意义的结论与成果，不过实际潜艇大多依靠螺旋桨驱动，其航行时同时存在艇体和螺旋桨的作用。研究表明，自航体的艇体阻力和螺旋桨推力是同时存在并相互作用的。若自航体处于加速或减速运动等非定常运动状态时，阻力和推力并不平衡，两者相互作用后会有额外动量传递给背景流体，在晚尾迹中形成大尺度相干涡结构[30-33]，成为一类内波激发源。对拖曳体而言，其运动时仅存在阻力动量，因此属于这种动量不平衡情况。若自航体处于匀速运动状态，阻力和推力平衡，则没有额外动量传递给背景流体，在其晚尾迹中不会形成大尺度相干涡结构，也不会激发大振幅的内波[34]。由此可见，潜艇的螺旋桨作用会对内波的特性产生重要影响，使用自航体模型进行内波实验研究，更具有实际意义。Gilreath等[35]采用电导率探头方法，测量分析了自航体生成内波特性，并认为自航体尾迹边界的湍动涡发生溃破产生随机内波。李万鹏等[36]采用电导率探头方法测量分析了密度分层流体中自航体生成内波的相关速度和位移场特性。最近，段宁远等[37]和Duan等[38]也采用电导率探头方法实验研究了分层流体中Suboff模型强迫自航（螺旋桨转速与拖曳速度不匹配）生成内波的相关特性问题。

目前对自航体尾迹生成演化特性问题已有一定的研究[30-40]，但迄今关于自航体内波生成机理及其表现特征问题的认识仍相当有限，因此本文以主体直径D=0.07 m、长L=0.56 m，具备指挥台、尾翼及螺旋桨等复杂附体结构的自航潜艇模型为对象进行内波实验研究。同时，考虑到螺旋桨的作用具有强烈的非对称性，因此沿水槽中纵剖面横向对称布置电导率探头阵列，结合相关性分析和奇偶函数分解等方法，对实验模型在匀速自航和拖曳两种状态下生成内波特性进行系列实验研究与对比分析，着重探究螺旋桨的作用对体积效应和尾迹效应内波时空形态特性的影响机理和规律。

1 实验系统与方法

实验在长12 m、宽1.2 m、高1 m的分层流水槽中进行。实验模型为具备自推进螺旋桨系统的潜艇模型，如图1所示。模型艇体由流线回转体形头部、圆锥形尾部及圆柱形中间部分组成，附体包括位于头部的围壳及位于尾部的十字型尾翼。艇体总长度为L=0.56 m，中间部分圆柱形的直径为D=0.07 m，即长径比λ=8。艇身用玻璃钢制作，内部腔体中空，用于配重及安装自推进系统。

实验模型潜深为d，即模型中间圆柱形部分的轴线到自由面的距离，而实验水深为h，如图2所示。采用两种方式驱动实验模型，一种是螺旋桨自推进驱动方法。在实验模型尾部安装一个直径为0.03 m的五叶螺旋桨，螺旋桨固定于特制驱动轴上，由一个量程为24 V的直流电机驱动螺旋桨旋转。直流电机通过两根细长导线连接到位于水槽外的量程为30 V的电压可调控的稳压直流电源上。内部轴系与实验模型之间采用黄油密封，以防止盐水对直流电机的侵蚀。细长导线从模型下方沉到水槽底部并从水槽一端伸出水面，使模型运动过程中导线始终在跃层下方，以保证其不对密度跃层产生扰动影响。

另一种是常用的循环拖曳法[12-14]，为保证自航运动和拖曳运动的单一变量对比原则，拖曳模型仍采用图1实验模型，循环拖曳方式见图2或参考文献[12-14]，不再赘述。

图1 实验模型Fig.1 Experimental model

图2 实验系统示意图（侧视）Fig.2 Schematic of the experimental system(side view)

在自航驱动和拖曳情况下，均让实验模型以速度U匀速运动。为保证实验模型的匀速自航，需要保证实验模型艇体阻力和螺旋桨推力的平衡。为此，首先根据实验模型艇体阻力和螺旋桨推力试验结果，在保证模型艇体阻力和螺旋桨推力平衡的要求下，确定模型运动速度U和螺旋桨转速n之间的关系。在此基础上，在密度分层水槽中对此关系进行标定修正，结果如图3 所示。由图可知，螺旋桨转速与模型自航速度之间为线性关系，而且实验模型最大自航速度可达1.8 m/s。

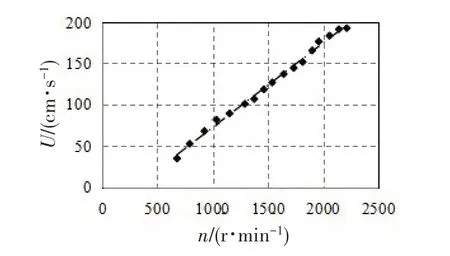
图3 螺旋桨转速n与模型自航速度U之间的关系Fig.3 Relationship between the self-propelled velocity U and the propeller rotational speed n

图4 所示为右手直角坐标系oxyz及电导率探头布置示意图，其中，oz轴垂直向下为正。所有探头垂向坐标相同，均为z=zP；第一组有23 个探头，x值相同而y方向间隔Δy1=0.05 m。第二组有8 个探头，与第一组探头的对应方式见图4，两组探头在x方向的间距为Δx=1.58 m。第一组探头用来测量模型运动生成的内波时空特征，两组y值相同的探头用来测量分析模型运动生成的内波沿x方向传播的相关速度。

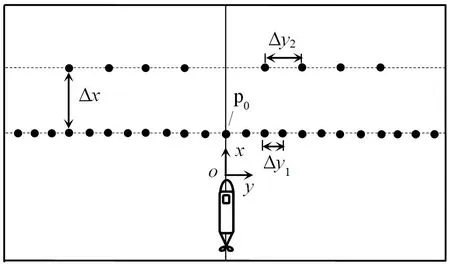
图4 坐标系和探头布置示意图Fig.4 Schematic of the coordinate system and arrangement of probes

本文采用强跃层密度分层流体开展系列实验，分层流体的密度随深度变化关系如图5（a）所示；定义浮力频率为N(z)=[(g/ρ)(∂ρ/∂z)]1/2，g为重力加速度，ρ为垂向密度分布，则分层流体的浮力频率随深度变化关系如图5（b）所示。由图5（b）可知，最大浮力频率Nmax=1.935 rad/s，在水面下z=0.25 m 处取得。为此，将各电导率探头置于zP=0.25 m处，重点研究该水平层在模型运动时生成的内波特性。

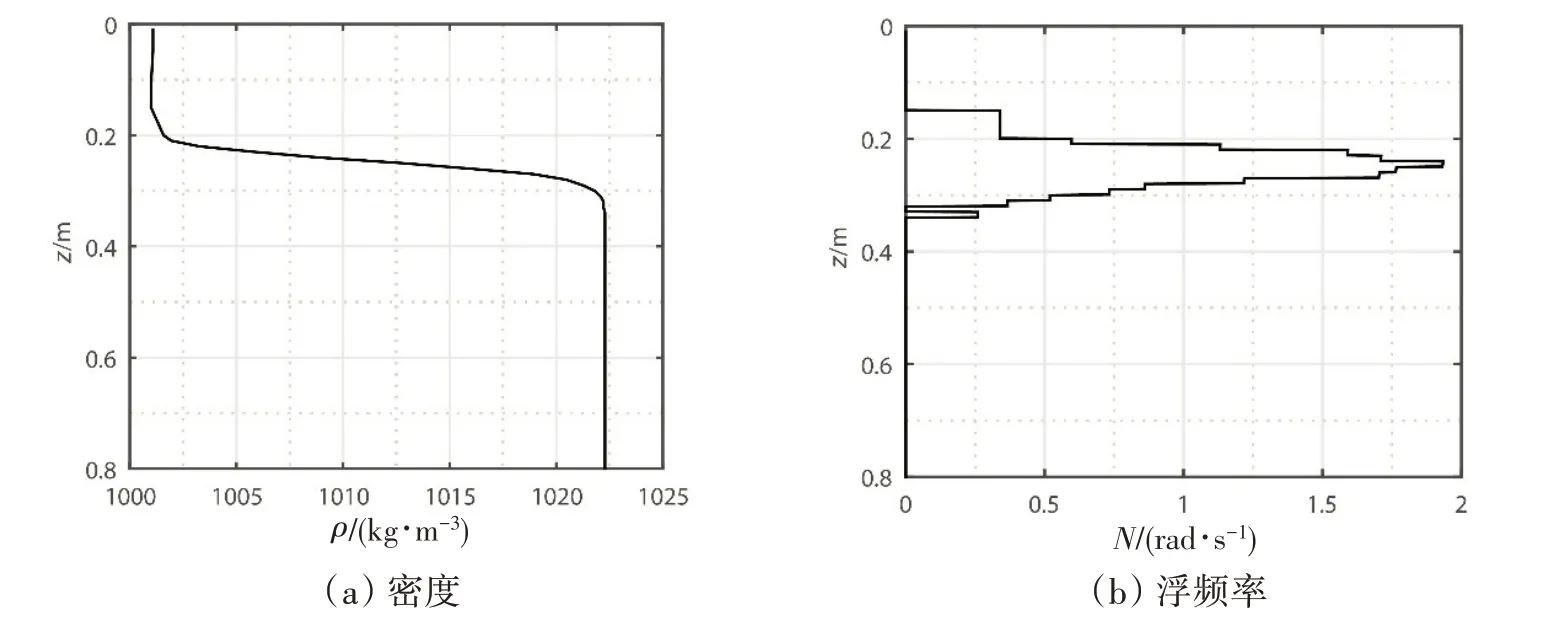
图5 密度和浮力频率随深度的变化关系Fig.5 Variation of density and buoyancy frequency with depth

根据文献[15]，探头处密度波动幅值与模型距探头垂向距离呈指数衰减关系。因此，实验模型不能距离探头太远，否则探头处波动不明显而受探头精度限制而失真。同时，考虑到螺旋桨的强烈作用可能造成密度跃层的快速混合塌陷而致使探头无法测得密度波动，因此实验模型中心轴线与电导率探头距离取适中值为0.15 m，即d=0.4 m。实验模型的运动速度范围为0.05 m/s≤U≤1.5 m/s，对应的Froude数Fr=U/DNmax的范围为0.3≤Fr≤11，Reynold数Re=UD/ν的范围为3500≤Re≤98 000。其中，ν为模型所在深度处盐水的动力学黏性系数。

2 结果与分析

2.1 内波相关波速转捩特性比较

本节比较分析拖曳和匀速自航下扰动产生体积效应和尾迹效应内波之间的转捩特性。对图4中两排y值相同的8 组探头测到的密度扰动时历分别进行相关性分析，相关性峰值对应时间记为Δt，定义内波相关速度为Uiw=Δx/Δt。其中Δx为两个探头之间的纵向距离。对内波相关速度进行无因次化处理，定义内波相关速度Froude数为Friw=Uiw/DNmax。

图6 给出了实验模型在拖曳状态下（为后文方便，记为“拖曳模型”或“拖曳体”）内波相关速度Froude 数Friw随Fr变化特性的实验结果。由图可知，存在一个临界Froude 数Frc≈3.40，当Fr＜Frc时，Friw≈Fr，表明在Fr＜Frc区间内拖曳模型运动生成的内波相对其运动是定常的；当Fr＞Frc时，Friw远小于Fr，且在0.7～1.4 范围内变化，表明在Fr＞Frc区间内拖曳模型运动生成的内波相对其运动是非定常的。

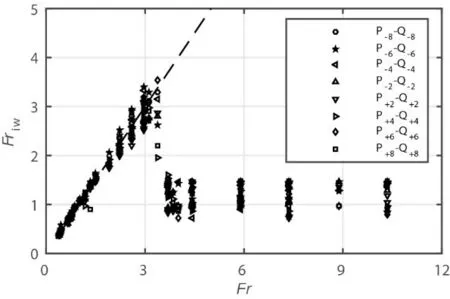
图6 拖曳模型产生内波相关速度Froude数Friw随Fr的变化特性Fig.6 Correlation velocity Froude numbers Friw versus towing Froude numbers Fr for the towed case

体积效应内波的激发源包括物体本身及其回流区产生的排水效应，这类激发源跟随物体一起运动，因此其产生的体积效应内波相对于物体的运动是定常的。尾迹效应内波的激发源较为复杂，包括近尾迹、尾迹塌陷及晚尾迹等，这类尾迹脱落后并不跟随物体一起运动，因此其产生的尾迹效应内波相对于物体的运动是非定常的。本文从内波相关波速随拖曳速度变化规律这一实验结果中同样表明了两类内波的产生机制及占优特性，即当Fr＜Frc时内波以体积效应内波为主，当Fr＞Frc时内波主要表现为尾迹效应内波。

对拖曳体运动产生两类内波的转捩特性问题，已有实验研究[9-16]均进行了报道。Robey[9]针对直径D=10 cm 的球体，获得临界Froude 数Frc≈2.0。王进等[12-13]进一步针对3个具有流线型头部的圆柱体模型（回转直径D=7 cm，长径比λ=4、7和9），发现Frc与长径比λ之间具有如下线性关系：

陈科等[16]进一步研究了2 个头部和尾部均为流线型的轴对称回转体（最大回转直径D=10 cm，长径比λ=5和8）在拖曳时激发内波的转捩特性问题，发现Frc与长径比λ之间具有如下线性关系：

式（2）中线性关系与式（1）略有不同，式（2）斜率略偏小。陈科等[16]将其归结为流线型头部和尾部影响了回流区长度，进而使得其有效长度比圆柱体等钝体型回转体的偏小。

本文实验模型的长径比为λ=8，将其代入式（1），可得Frc=3.67；若将其代入式（2），可得Frc=3.24。本文拖曳实验结果Frc≈3.40处于两者之间，后者预测结果更为接近。

本文实验模型为头部流线型而尾部带尾翼和螺旋桨的全附体潜艇模型，其有效长度介于式（1）和式（2）所用模型之间。同时，本文实验模型平行中体部分带有围壳，相当于增加了部分回转体的有效直径，因此本文拖曳实验结果在上述两个经验预测公式之间是合理的。

对转捩后内波相关速度Froude 数Friw的变化特性问题，Robey[9]和王进等[12-13]的研究发现，尾迹效应内波的相关速度Froude 数Friw在常数0.8 附近有小幅波动。由图6 可知，转捩后在不同纵剖面上内波相关速度Froude 数Friw下降的幅度有较大差异，而且随着Froude 数Fr的变化，Friw并没有在常数0.8附近出现小幅波动的现象，而是在0.7～1.4之间的一个条带内变化，变化幅度达0.7。这表明，由于尾迹效应内波的时空随机特性，其在不同纵向剖面上相关速度Froude 数Friw的变化幅度是不一样的。因此，目前文献[9-13]仅从某一个纵向剖面来研究尾迹效应内波相关速度Froude数Friw特性是不全面的。

下面分析实验模型在匀速自航下（为后文方便，记为“自航模型”或“自航体”）产生内波相关速度Froude数Friw随Froude数Fr变化特性问题，结果如图7所示。由图可知，在匀速自航下，也存在一个临界Froude 数Frc≈2.95，当Fr＜Frc时，Friw≈Fr，表明在Fr＜Frc区间内自航模型运动生成的内波相对其运动是定常的；当Fr＞Frc时，Friw远小于Fr，且在0.4～1.5范围内变化，表明在Fr＞Frc区间内自航模型运动生成的内波相对其运动是非定常的。

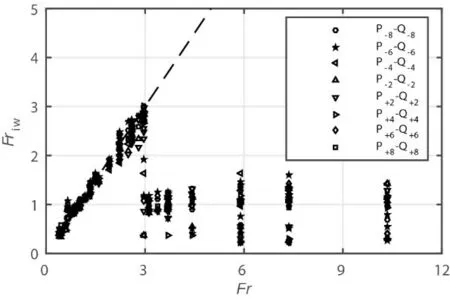
图7 定常自航模型产生内波相关速度Froude数Friw与Fr的变化特性Fig.7 Correlation velocity Froude numbers Friw versus Froude numbers Fr for the self-propelled case

由此可见，匀速自航模型扰动也产生两类内波，一类为定常的体积效应内波，另一类为非定常的尾迹效应内波。同时，与模型拖曳扰动产生的尾迹内波类似，对匀速自航模型扰动产生的尾迹内波，在不同纵剖面上尾迹内波相关速度Froude 数Friw下降的幅度也有较大差异，而且随着Froude 数Fr的变化，Friw在0.4～1.5 之间一个较大范围的条带内变化，变化幅度达1.1。

结果表明，在模型匀速自航的情况下，内波临界Froude 数要小于模型拖曳的情况。造成这个差异的主要原因是：由于螺旋桨叶片的搅拌效应，与拖曳的情况相比，自航物体尾流区的平均速度衰减更快，尾迹更容易进入湍流状态[31]，这表明尾迹效应内波更容易在较小的自航速度下成为主控内波。由此可见，推进器效应对内波转捩特性有明显影响，推进器效应会使尾迹效应在较小的自航速度下就超过体积效应，出现尾迹效应主控的内波。

李万鹏等[36]对一个长径比为λ=8.3的轴对称回转体在7叶螺旋桨驱动下产生的内波特性问题进行了实验研究，其中螺旋桨采用直流电机进行无线遥控驱动，测量分析了实验模型在加速运动状态下产生内波的转捩特性，获得的临界Froude 数Frc≈4.4。由此可见，水下物体在定常和非定常自航状态下，产生内波的转捩特性有明显差异，这是在研究自航体产生内波特性问题时需要特别注意的问题之一。

本文实验模型是由一个实际的全附体潜艇经几何缩比后制作的，因此本文实验所得自航模型扰动产生内波的转捩特性，对研究实际潜艇在密度分层海洋中激发内波特性更具有参考意义。实际海洋中海水密度垂向不同，也存在分层现象，其最大浮频率通常在0.01～0.02 rad/s 之间。假设潜艇的最大回转直径为D=12 m，那么由本文实验结果可知，在潜艇定常自航的情况下，界定两类内波占优区间的临界航速为Uc=FrcDNmax=0.35～0.7 m/s。实际潜艇的航速一般在2 kn（≈1 m/s）以上，这意味着在实际海洋中定常航行潜艇扰动产生的内波主要以尾迹效应内波为主控内波。

2.2 内波峰-峰值特性比较

探头测得的电导率波动时历可通过电导率与密度的标定关系转化为密度波动时历，密度波动时历又可通过密度剖面转化为位移波动时历。记垂向位移波动时历最大峰-峰幅值为Hm，取其无量纲形式为Hm/D。图8给出了拖曳和自航下Hm/D随Froude数Fr变化特性的实验结果。

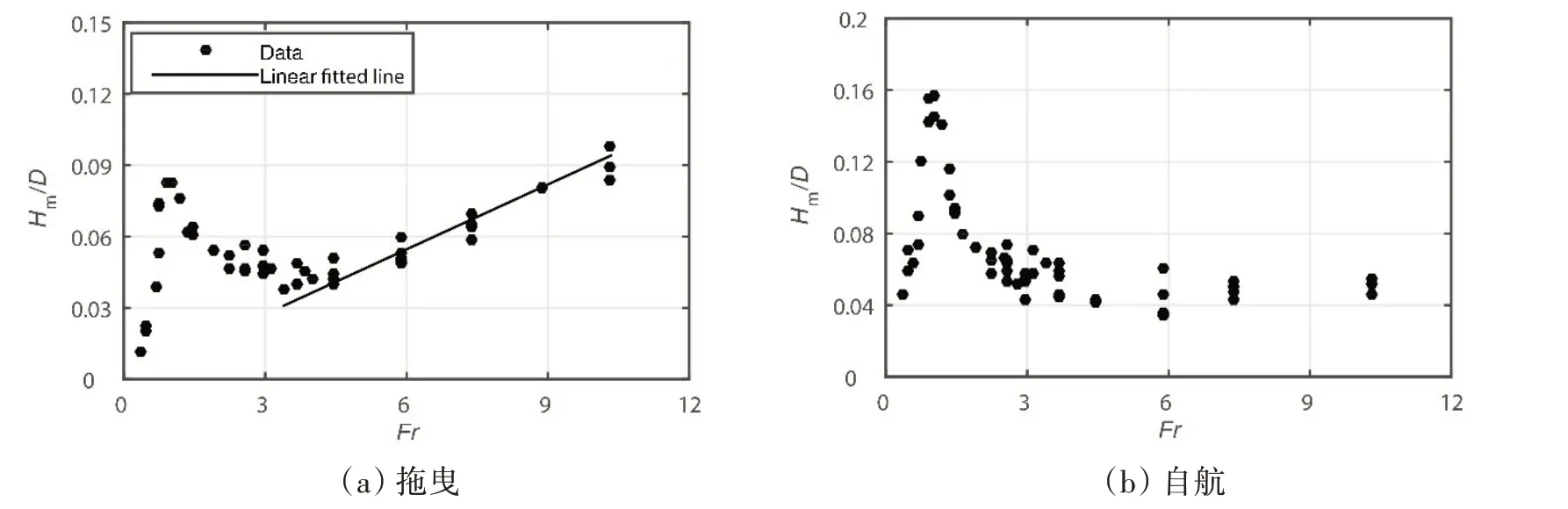
图8 在拖曳和自航下Hm/D随Fr的变化特性Fig.8 Hm/D versus Fr for the towing and self-propelling cases

由图8 可知，对两种模型运动方式，在各自转捩点之前，Hm/D曲线均出现一个峰值，其对应的Froude数均近似为Frp≈1.03，当Fr＜Frp时，Hm/D随Fr增大而增大；当Frp＜Fr＜Frc时，Hm/D随Fr增大而减小。在各自转捩点之后，模型拖曳情况下，Hm/D随Fr增大近似线性增大；但模型定常自航下，Hm/D随Fr增大并没有线性增大，而是在0.04～0.07之间的一个条带内变化。这意味着转捩后定常自航模型与拖曳模型产生内波的位移场特性有明显差异，这进一步表明两种运动方式下尾迹效应内波的激发源特性是有明显差异的。

关于转捩前体积效应内波波高（波幅）随拖曳Fr的变化规律，针对球体和细长回转体，已有实验研究[9-16，23]均得到先增大后减小这一规律，只是峰值对应Froude 数Frp有所不同。对于拖曳球，Chomaz等[23]得到Frp=0.5～0.6，Robey 等[9]得到Frp=0.7～0.8。对于具有流线型头部和圆柱形尾部的细长体，王进等[12-13]发现Frp与长径比λ之间也存在线性关系：

对于具有流线型头部和流线型尾部的细长体，陈科等[16]发现Frp与长径比λ之间的线性关系为

本文实验模型的长径比为λ=8，将其代入式（3），可得Frp≈1.49，其值大于本文实验结果；若将其代入式（4），可得Frp≈0.96，其值与本文实验结果一致。表明本文实验模型的有效长度小于同长度圆柱体的提法是合理的。

关于转捩后尾迹效应内波波高（波幅）随拖曳Fr的变化规律，针对球体和细长回转体，已有实验研究[9-16]和本文拖曳下的结果均得到波高随Fr增大而增大这一规律，并认为这一规律主要由晚尾迹中大尺度相干涡结构产生的移动排水效应造成的。这类大尺度相干涡结构具有自保持特性并对物体形状没有记忆效应[27-28]，其产生的移动排水效应主要与物体回转直径、潜深及运动速度有关[9，14]，而与长径比无关[13，15-16]。

在物体自航的情况下，艇体效应相当于给背景流体传递一个阻力动量，而推进器效应相当于给背景流体传递一个射流动量，两者的作用效果正好相反，前者为正动量，而后者为负动量。当物体作定常自航时，阻力与推力平衡，物体运动并不给背景流体传递净动量，此时物体运动产生的尾迹不会形成大尺度相干涡结构[32-34]。虽然物体定常自航时其尾迹中湍流涡脉动、尾迹塌陷及其产生的排水效应也会产生内波，但这类内波的激发源都是一些小尺度随机现象。本文结果表明，这类小尺度随机现象激发内波的峰-峰幅值并不随物体定常自航速度增大而增大，而是在某个范围内随机地变化。这进一步表明，尾迹效应内波波幅变化规律与驱动方式有关。因此，早期用拖曳体运动产生内波特性来模拟实际靠螺旋桨等驱动的潜艇运动产生内波特性是不合适的。

假设水下航行体的最大回转直径为D=12 m，可得实艇与模型之间的几何相似比为1200∶7。在本文实验中，主跃层深度为0.25 m,实验模型中心轴线到主跃层的距离为0.15 m。经换算可得实艇中心轴线到主跃层的距离为25.71 m,而实际的主跃层深度为42.85 m，这与夏季实际海洋中的主跃层深度一致。根据图8 所得实验结果，经换算可知，在水下航行体定常自航的情况下，其扰动产生尾迹内波的峰-峰幅值范围近似在0.48～0.84 m 之间。由于尺度效应等因素，这些结果仅作为一个初步的预测。不过，可以确信的是，当潜艇在密度分层海洋中作定常自航航行时，其艇体和推进器扰动产生内波的峰-峰幅值很小，在这种情况下海面的响应也会变小，是否足以产生可被SAR 探测的有效信息还需进一步的研究论证。

当物体作加速或减速等非定常运动时，阻力与推力不平衡，此时给背景流体传递一个净动量。该净动量在密度分层流体的浮力效应作用下形成晚尾迹，并产生大尺度相干涡结构[31-33]。但有关这类大尺度相干涡激发内波特性以及能否在水面产生可被SAR探测的有效信息等问题，目前尚不清楚。

2.3 内波时空特性比较

本节从内波时空特性的对称性角度入手，对拖曳和自航体产生内波的时空特征进行比较分析。为此，设Δz=Δz（y,t）为在点（0,y,zP）处内波位移的时历。众所周知，对任意一个实函数，均可唯一地分解为一个偶函数和一个奇函数之和。据此，将Δz分解为关于y的偶函数和奇函数两个成分：

式中，Δzs描述了关于物体中心轴线正对称的内波成分，Δza描述了关于物体中心轴线反对称的内波成分。

记（cpm）0为第m模态的内波临界相速度。那么，根据等相线理论[6]，当内波激发源移动速度Us＜（cpm）0时，该模态内波既有横波又有散波；当Us＞（cpm）0时，该模态内波没有横波而仅有散波。对本实验所用的分层流体，经等相线理论计算可得：（cp1）0=17.8 cm/s，（cp2）0=3.6 cm/s。

利用式（5），分离出内波位移时历的正对称和反对称成分，进一步分析其时空形态特征。首先考虑拖曳的情况，其中内波的临界转捩速度约为46 cm/s。图9 给出了转捩前内波正对称和反对称成分的时空形态特征。图中纵坐标范围为[0,120]（单位为s），表示时间；横坐标范围为[-0.55,0.55]（单位为m），表示沿水槽宽度方向。

图9 拖曳情况下转捩前正对称和反对称成分的时空波形图Fig.9 Time-space wave patterns of symmetric and anti-symmetric components before transition for the towed case

由图9 可知，在转捩前，内波反对称成分在较小拖曳速度时，没有明显的V 字形结构，当拖曳速度接近临界转捩速度时，开始出现明显的V 字形结构，这表明随着拖曳速度的增大，尾迹效应内波的影响逐渐增强。对内波正对称成分，当U=6、10、14 cm/s 时，可以观察到两个波系，一个为内层既有横波也有散波的波系，另一个为外层仅有散波的波系。根据等相线理论，内层波系为第一模态内波，而外层波系为第二模态内波。当U=20、30、35 cm/s时，由于U＞（cp1）0，因此第1模态内波只有散波。

其次考虑定常自航的情况，其中内波的临界转捩速度约为40 cm/s。图10给出了转捩前内波正对称和反对称成分的时空形态特征。由图可知，在转捩前各个自航速度下，内波正对称成分中均可见两类明显的V 字形结构，其中张角较小的内层V 字形结构出现的时间（记为t0）要晚于张角较大的外层V字形结构，而且随着自航速度的增大，t0随之减小。但在内波反对称成分中，只可见一类明显的V字形结构，而且其出现时间和特征均与正对称成分中张角较小的内层V字形结构一致。

图10 自航情况下转捩前正对称和反对称成分的时空波形图Fig.10 Time-space wave patterns of symmetric and anti-symmetric components before transition for the self-propelled case

为进一步说明定常自航体产生内波中两类V 字形结构的生成机理，图11 给出了3 个速度下探头P0处拖曳和定常自航体产生内波位移时历特性。结果表明，在各个速度下均存在一个时刻t0，当t＜t0时，两者时历的相位一致，而当t＞t0时，两者时历相位开始出现差异。对拖曳的情况，由前面的分析已知，在转捩前尾迹效应内波的影响很小，内波主要成分为正对称的体积效应内波。基于这个事实，结合图9 和图10 的观察结果，可知转捩前定常自航体产生内波正对称成分中先出现的外层V 字形结构为体积效应内波，而内波正对称成分中晚出现的内层V 字形结构及反对称成分中的V 字形结构均为尾迹效应内波。

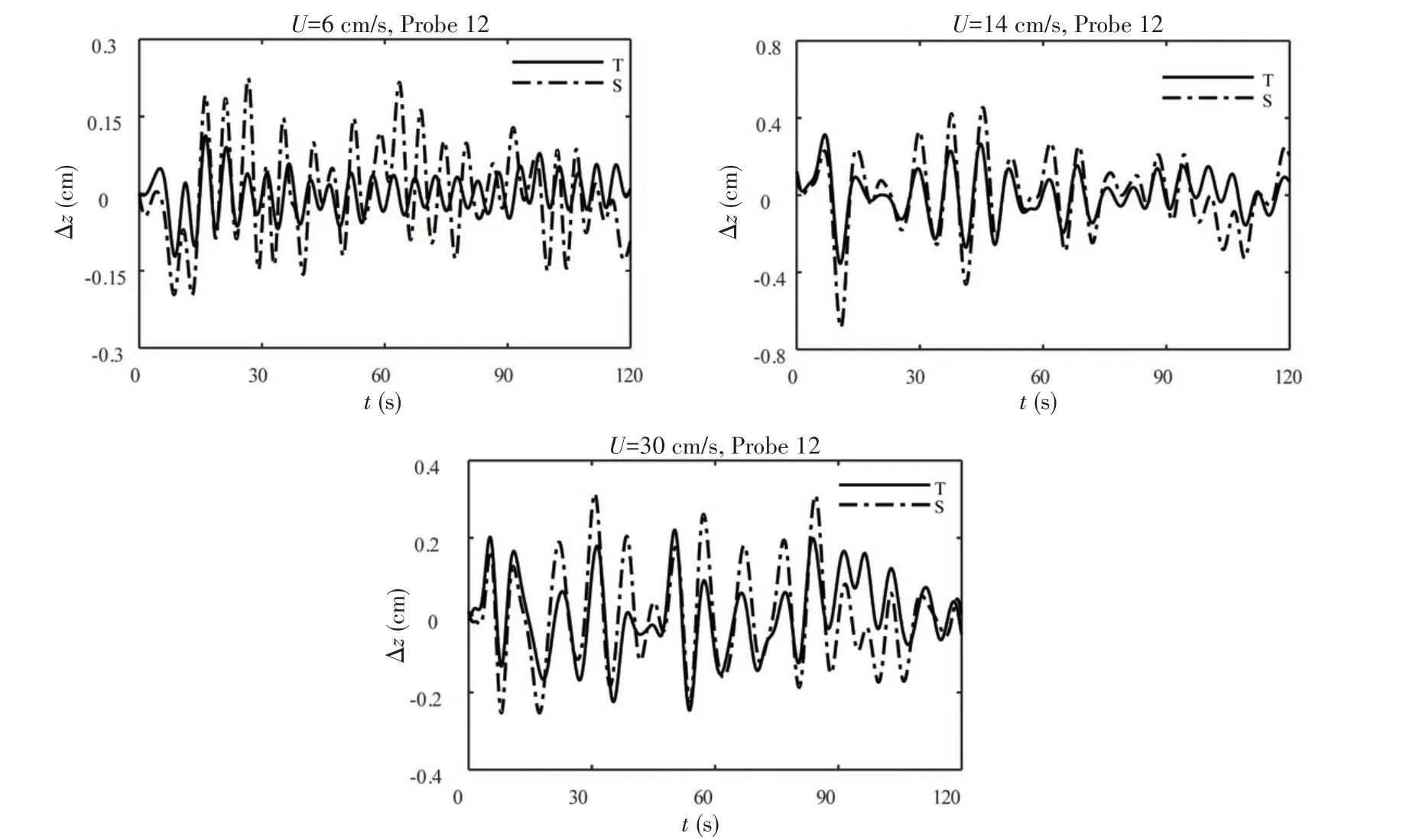
图11 转捩前探头P0（Probe 12）处拖曳和定常自航情况下内波位移时历比较（T为拖曳，S为自航）Fig.11 Time histories of Δz for the towed(T)and self-propelled(S)cases before transition of P0(Probe12)

下面比较分析转捩后拖曳和自航体产生内波的时空形态特征。首先考虑拖曳的情况，结果如图12 所示。由图可知，在各个拖曳速度下，内波正对称成分中可见两类V 字形结构，其中张角较小的内层V 字形结构出现的时间要晚于张角较大的外层V 字形结构，而内波反对称成分中仅可见一类张角较小的V 字形结构，这意味着张角较大的V 字形结构关于水槽中纵剖面是对称的，这类内波成分为第一模态的体积效应内波，由于U＞（cp1）0，因此这类内波成分只有散波。对内波正对称和反对称成分中张角较小的V 字形结构，在各拖曳速度下其空间形态特征相似，而且既有散波又有横波，这类内波成分是不对称的，属于尾迹效应内波。

图12 拖曳情况下转捩后正对称和反对称成分的时空波形图Fig.12 Time-space wave patterns of symmetric and anti-symmetric components after transition for the towed case

其次考虑转捩后定常自航体产生内波的时空形态特征，结果如图13 所示。由图可知，在各个自航速度下，内波正对称成分中也可见两类V 字形结构，张角较大的外层V 字形结构出现较早，为体积效应内波；而张角较小的内层V 字形结构出现较晚，为尾迹效应内波。对外层的正对称体积效应内波，由于U＞（cp1）0，因此只有散波；而对内层的正对称尾迹效应内波，则既有散波又有横波。此外，对内波反对称成分，也清晰可见一类张角较小的V字形结构，而且其时空形态特征与内波正对称成分中张角较小的V字形结构相似。这类内波成分关于水槽中纵剖面不是对称的，同样属于尾迹效应内波。

图13 自航情况下转捩后正对称和反对称成分的时空波形图Fig.13 Time-space wave patterns of symmetric and anti-symmetric components after transition for the self-propelled case

对于转捩后的尾迹效应内波，虽然定常自航和拖曳下的波峰-峰幅值差异较大，但其波形结构中均出现一类既有正对称也有反对称的张角较小的V 字形结构，该结构晚于正对称波形中较早出现的外围张角较大的波系，结合图6 和图7 的波速图可知，该结构主要是移动速度远小于拖曳或自航速度的尾迹效应内波。

3 结 论

本文利用大型密度分层水槽，对密度分层流体中长径比为8:1的自航模型在定常自航和拖曳下运动产生内波特性问题进行了系列实验。利用沿水槽中纵剖面对称布置的电导率探头阵列测量技术，结合相关性和奇偶函数分解等方法，从内波相关波速转捩特性、峰-峰值特性和时空形态特征等方面，对两种运动方式下内波生成机理及其表现特征问题进行了全面的比较分析研究，获得如下主要结果：

（1）在两种运动方式下，均存在一个临界Froude 数Frc，当Fr＜Frc时，内波相关速度等于物体运动速度，体积效应内波为主控内波；当Fr＞Frc时，内波相关速度小于物体运动速度，尾迹效应内波为主控内波；拖曳方式下Frc≈3.40，定常自航方式下Frc≈2.95，小于拖曳方式下的临界值，表明推进器效应会使体积效应内波衰减更快，在较小航速下尾迹效应内波即可成为主控内波；在转捩后，尾迹效应内波相关速度变化具有时空随机性，在拖曳方式下其变化范围为0.7～1.4，而在定常自航方式下其变化范围为0.4～1.5。

（2）在转捩前，两种运动方式下均存在一个近似相同的Froude 数Frp=1.03，当Fr＜Frp时，内波最大峰-峰幅值随Fr增大而增大；当Frp＜Fr＜Frc时，内波最大峰-峰幅值随Fr增大而减小；但在相同Froude数（Fr）下，定常自航体产生内波峰-峰幅值要比拖曳情况大，这表明推进器效应也会产生体积效应，而且与艇体的体积效应形成正叠加。在转捩后，拖曳方式产生内波的无因次最大峰-峰幅值随Fr增大而近似线性增大，但定常自航体产生内波的无因次最大峰-峰幅值并不随Fr增大而增大，而是在0.04～0.07范围内变化，这表明推进器的作用会对尾迹效应内波波幅产生较大影响。

（3）从内波时空形态特征上看，体积效应内波是对称的；而尾迹效应内波是不对称的，既存在正对称成分，也存在反对称成分，且均呈V形结构。

本文结果表明：实际潜艇匀速航行时，其产生内波以转捩后尾迹效应内波为主，此类内波峰-峰幅值很小，这种情况下是否能在海面产生可被SAR 探测的有效信息还需开展针对水面特征的实验进行论证；另一方面，自航体在加速/减速等非定常航行状态下的内波表现特征可能与定常匀速自航的情况有所不同，也值得进一步的关注。