基于ABC-RFEKF算法的锂电池SOC估计

寇发荣，王甜甜，王思俊，张 宏，门 浩

基于ABC-RFEKF算法的锂电池SOC估计

寇发荣，王甜甜，王思俊，张 宏，门 浩

(西安科技大学机械工程学院，陕西 西安 710054)

准确、可靠的荷电状态(SOC)估计可以为电池管理系统的安全高效使用提供保障。针对锂电池SOC估计精度不足的问题，提出人工蜂群算法(ABC)和随机森林优化EKF算法(RFEKF)分别实现电池模型的参数辨识和SOC估计。在建立双极化模型的基础上，为解决在线辨识初始误差累积的问题，采用ABC算法搜索最小模型电压误差下的全局最优阻抗参数值，实现模型参数的精确辨识。在获得精确的模型参数基础上，使用随机森林(RF)对SOC后验估计误差进行在线补偿，达到弥补传统EKF算法高阶项误差的目的，进而实现SOC高精度估计。联合半实物仿真系统和电池测试平台，在EPA城市动力工况下对SOC估计算法实现快速控制原型验证。结果表明：基于ABC-RFEKF的锂电池SOC估计算法各项误差指标均低于传统SOC估计算法，平均误差在1%左右，满足实际工程需求。

荷电状态；人工蜂群算法；随机森林；扩展卡尔曼滤波；快速控制原型

0 引言

随着新能源汽车市场的扩大，动力性锂电池需求量也大幅提升。锂电池SOC作为电池管理系统剩余可用能量评估的重要指标之一，其准确估计为电动汽车的安全管理、充放电控制、整车能量管理等功能提供参数支持[1-5]。

精确的锂电池模型参数辨识是提高SOC估计精度的前提与保障。文献[6]提出基于渐消记忆递推最小二乘法的参数辨识方案，进而实现电动汽车电池荷电状态在线估计；文献[7]提出一种可变窗口的最小二乘法，利用可变窗口特点截取工况信息实现参数辨识和SOC估计；文献[8]中提出一种带遗忘因子的偏差补偿递推最小二乘法，进行有色噪声干扰下参数辨识。以上参数辨识方法均为递推最小二乘法的衍生算法，对于持续缓慢变化的启发式系统，无法解决在线参数辨识初始阶段辨识不精确的问题，严重依赖旧数据，甚至大幅降低参数辨识的精度。

为实现锂电池SOC的高精度估计，文献[9]提出一种基于强跟踪扩展卡尔曼滤波的锂电池SOC估计方法；文献[10]选用双自适应无迹卡尔曼滤波算法估算电池的SOC值；文献[11]提出粒子群(PSO)优化极限学习机(ELM)神经网络方法提高电池SOC估算精度；文献[12]提出使用改进的天牛须算法优化扩展卡尔曼滤波的噪声协方差矩阵，提高了SOC的估计精度；文献[13]提出一种基于数据驱动的改进扩展卡尔曼滤波算法实现动力电池全生命周期SOC估计；文献[14]利用变分贝叶斯方法将系统状态和虚拟观测噪声协方差作为待估参数并行估计，提高了SOC估计精度。以上方法均能实现SOC在线估计，但估计过程中状态方程近似线性化过程忽略了高阶项，导致估计结果准确性有所降低。

提高SOC估计精度需从提高参数辨识精度和SOC算法精度两方面入手，分别设计了人工蜂群(ABC)参数辨识算法和随机森林优化扩展卡尔曼滤波(RFEKF)SOC估计算法。本文在建立双极化模型和OCV模型的基础上，以模型端电压误差作为适应度函数，使用元启发式优化算法中的ABC搜索算法完成双极化模型最优参数的求解；使用训练完成的RF算法预测SOC估计后验误差，并对扩展卡尔曼滤波算法的高阶误差项进行补偿与修正，从而提高SOC的估计精度。最后对模型参数辨识精度和SOC算法估计精度进行在线快速控制原型(RCP)验证。

1 锂电池模型的建立

1.1 双极化模型

等效电路模型的准确建立是SOC估计的第一步，双极化模型即二阶RC等效模型是一种较好的电池估算模型，同时考虑了电池的动态特性和静态特性，其模型的拓扑结构如图1所示。其中cap为电池容量。

该等效电路模型的微分方程为

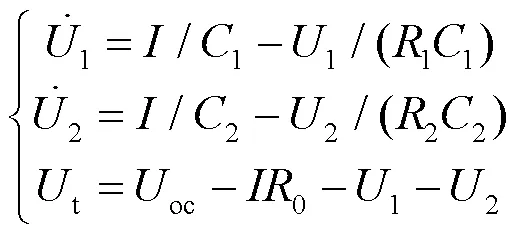
式中：R0为欧姆内阻；R1、R2、C1、C2分别为电化学极化和浓差极化的电阻、电容；U1、U2为电化学极化电压和浓差极化电压；Ut为端电压；Uoc为开路电压。

1.2 开路电压模型

试验对象为方型硬壳锂电池，其标称容量为32 Ah，上下截止电压为3.7～4.2 V。选用艾德克斯动力电池测试系统进行试验，试验系统的接线布局如图2所示。系统包含可编程直流电源IT6724、功率耗散器IT8514C+和温度采集仪IT5601。同时使用上位机控制电源和负载协同工作，完成实验数据的采集。

图2 动力电池测试系统

OCV-SOC关系曲线是SOC估计的重要一步，其曲线精度直接影响SOC的准确性。根据《混合动力车用HPPC规范》[15]电池手册得，OCV采集点需要在离线状态下测量得到，故采用恒电流间歇滴定技术实现OCV的标定。试验中充放电倍率为1C，静置时间为3 600 s。并使用Lsqcurvefit函数对OCV曲线进行六次多项式拟合得

2 模型阻抗参数辨识

模型阻抗参数的精度[16-17]是衡量所建模型能否准确表达真实电池充放电特性的关键。由于传统的递推最小二乘法进行在线参数辨识过程中存在初始阶段辨识不精确的问题，导致误差累积，甚至大幅降低参数辨识的精度，进而影响SOC估计精度。

图3 人工蜂群算法流程图

1) 初始化种群。标准的ABC算法将优化问题看作是5维搜索空间的求解过程。假设引领蜂、观察蜂和蜜源的数量都相等，蜜源的好坏取决于花蜜量的多少，用“适应度函数”来评判。初始化参数值如表1所示。

表1 初始化参数

3) 根据引领蜂搜索蜜源的好坏判断。当新蜜源优于原蜜源时，更新蜜源位置，这时引领蜂根据轮盘赌[20]的方法，招募观察蜂，并计算观察蜂的跟随概率如式(5)所示；相反，当新蜜源劣于原蜜源时，引领蜂的说服力会降低，这时引领蜂变为侦察蜂。

式中，为目标函数。

4) 观察蜂根据贪婪选择法[21]，在邻域搜索蜜源

如式(3)所示，再根据式(4)计算适应度函数。根据蜜源好坏选择，当新密源优于原蜜源时，更新蜜源位置，则观察蜂变为引领蜂，继续寻找新蜜源；当新蜜源劣于原蜜源时，观察蜂变为侦察蜂。

5) 侦察蜂继续邻域搜索蜜源如式(3)所示，再根据式(4)计算适应度函数。当新密源优于原蜜源时，侦察蜂找到高质量蜜源，这时侦察蜂再次做回引领蜂；当新蜜源劣于原蜜源时，侦察蜂变为观察蜂，继续找寻蜜源。

完成步骤1)—步骤5)的迭代过程，通过寻找最优蜜源位置，得到最小电压误差下的最优阻抗参数值，即可以实现锂电池双极化模型最优阻抗参数的精确辨识。使用ABC算法在UDDS工况下的参数辨识结果如图4所示，通过寻优得到的模型参数值如表2所示。

表2 双极化模型参数

图4 参数辨识结果

3  锂电池SOC估计

3.1 扩展卡尔曼滤波算法

EKF算法的迭代过程如下。

1) 系统变量初始化

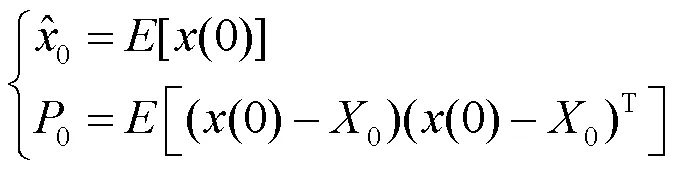
2) 迭代过程为

3.2 随机森林优化扩展卡尔曼滤波算法

在EKF估计SOC过程中，EKF用非线性系统模型方程代替线性系统模型方程，将系统开路电压模型求偏导来实现模型线性化。因忽略高阶项带来的误差，导致单独使用EKF估计电池SOC过程中产生较大的误差。因此，本文提出RFEKF算法[22-24]解决上述问题，即使用随机森林算法(RF)对EKF进行补偿和优化，进一步提高SOC估计精度。

3.2.1随机森林

随机森林(RF)[25-26]是由许多个决策树[27-28]组合而成，利用自主抽样法从原数据中有放回地抽取多个样本，对抽取的数据用决策树进行训练，把这些决策树组合在一起，形成森林。与决策树算法相比，随机森林具有决策树的优点，而且不容易产生过拟合，并且在生成多个决策树的过程中可利用CPU的多核结构进行并行处理。

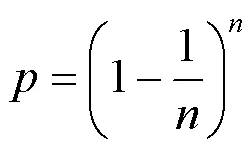
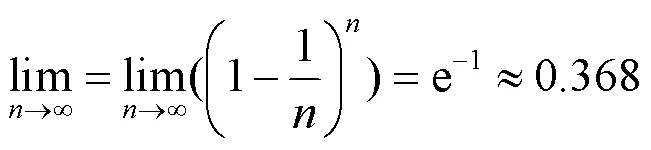
虽然，新集合1和原来的集合中样本数目相等，都有个样本数，但是新集合中可能包含了重复的样本，若除去重复抽样的重复样本，新集合1中仅包含了原来集合中1-0.368×100%=63.2%。详细流程如下：

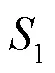
3) 每棵树都完整成长，而不进行剪枝。

5) 采用投票的方法，将个决策树中输出最多的类别作为测试集样本所属的类别。

3.2.2 RFEKF算法设计

随机森林对EKF算法的优化，弥补了EKF的非线性误差，提高SOC估计精度；随机森林的自学习能力和对函数的逼近能力，使得此算法对电池模型精度要求不高。具体优化过程如下。

2) 使用随机森林对EKF算法进行补偿，结构如图5所示。该算法本质为，使用训练完的随机森林预测出SOC后验估计补偿误差，即SOC真实值与估计值之间的误差，完成对EKF的后验状态估计值的修正，从而使SOC更加精确。精准的SOC估计值会决定下一时刻的量测矩阵值，因此SOC值的精确估计影响全局。

图5 RFEKF算法结构图

4  实验结果和分析

4.1 快速控制原型试验设计

本文将基于DSPACE公司生产的MicroAuto Box硬件进行算法模型的快速控制原型(RCP)[29]验证，快速控制原型验证平台如图6所示。通过搭建半实物仿真实验平台，将PC端Matlab/Simulink搭建的控制算法模型、硬件MicroAuto Box、动力电池测试系统三者结合起来，运用MicroAuto Box的I/O接口技术实现电池信号的接收，完成算法的在线验证。

图6 快速控制原型验证平台

4.2 模型精度分析

为了验证所建模型精度的准确性，以美国环境保护局(EPA)规定的城市动力工况(UDDS)作为验证工况。该工况通过模拟实际电动汽车行驶工况中电流激励，进行锂电池动态性能测试，测试时长为20 000 s。图7为模型端电压对比及误差曲线。

由图7可得，在放电初期，相对于在线参数辨识方案，基于ABC算法的参数辨识方案初始阶段误差相对较小，能够解决放电初始阶段辨识不精确的问题，大幅提高参数辨识的精度。说明ABC算法能通过引领蜂的局部寻优行为，使侦察蜂在全局中更好地跟随最优值；在放电中、后期，ABC模型端电压比传统在线模型端电压误差稍低，波动更为平稳。详细的误差分析如表3所示。

表3 传统在线辨识和ABC辨识端电压误差分析

由表3可得，在UDDS工况下，相较于传统在线辨识方案，基于ABC算法的参数辨识方案最大误差降低了79.8%，平均误差降低了38.2%，均方根误差降低了39.2%。数据表明，基于ABC算法的参数辨识方案能解决初始阶段辨识不精确的问题，实现锂电池模型的精确参数辨识。

4.3 RFEKF算法精度分析

为进一步验证RFEKF算法[30]对SOC估计的准确性，本文选用更符合实际情况的UDDS工况，利用搭建的半实物仿真平台，进行RCP在线验证。将实际得出的SOC估计值与传统EKF算法和RFEKF算法得出的SOC值作对比，如图8所示。图8(b)和图8(c)为图8(a)初期和后期的局部放大图，图9为SOC估计误差。

由图8(a)可知，RFEKF、EKF算法和工况试验SOC曲线趋势基本一致，RFEKF算法曲线能快速收敛至真实SOC值附近，能够较好地实现SOC的精确估计。由图8(b)可得，RFEKF比EKF算法更接近真实值，而且在放电初期，初始化参数收敛速度较快，说明RFEKF算法能更准确描述电池的特性。由图8(c)可知，在短时间大电流放电时，SOC急剧降低，RFEKF算法相较于传统EKF算法能够快速收敛至真实SOC值附近，表明RFEKF算法的抗干扰性更强。整体来看，优化后的算法能够更好地估计出实时的SOC，并且误差较为稳定，即使出现误差较大的点，也能快速收敛至真实值附近。由图9可得，EKF算法因忽略高阶项，使误差累积，导致SOC估计后期误差偏大，而RFEKF算法仍能实现精确的SOC估计，误差基本稳定，原因是RF算法补偿和优化了EKF算法高阶项误差。详细误差统计分析如表4所示。

图8 RFEKF联合估计和标准EKF估计曲线对比

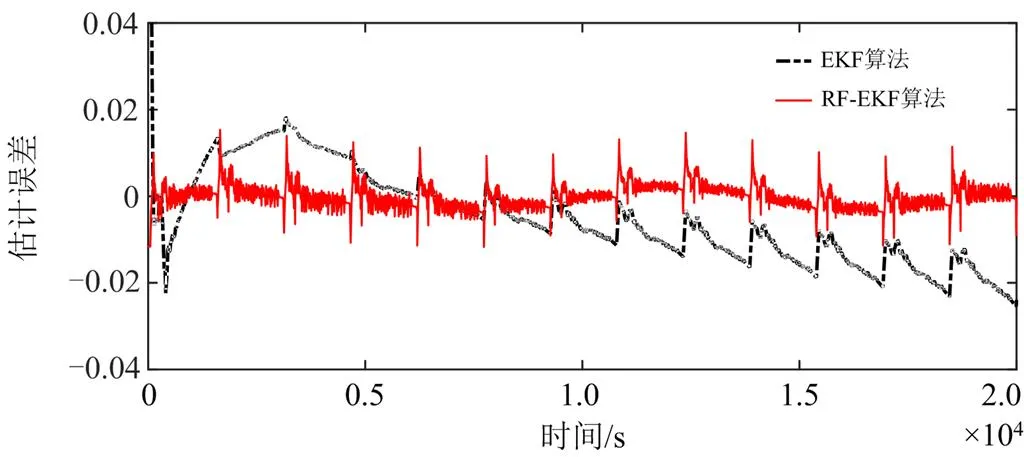
图9 RFEKF联合估计和标准EKF估计误差曲线对比

表4 RFEKF算法和EKF算法误差统计分析

由表4可得，在UDDS工况下，基于RFEKF的SOC估计算法误差指标远低于传统EKF算法。相比于传统的EKF算法，RFEKF算法的最大误差降低了24.2%，平均误差降低了32.8%，均方根误差降低了45.8%。数据表明，采用随机森林对EKF算法的状态后验估计误差进行补偿与修正，解决了传统EKF算法中的线性化高阶项误差累积问题，从而提高锂电池SOC估计精度。

5 结论

为实现SOC高精度估计，提出ABC参数辨识寻优算法和电池SOC估计的RFEKF算法，得出以下结论：

1) 采用ABC算法完成双极化模型的参数辨识，解决了模型参数初始化阶段辨识不精确的问题。通过模型端电压精度验证，试验结果表明，模型端电压与试验端电压曲线趋势基本一致；模型端电压平均误差为0.039 7 V，说明该参数辨识方案能够实现锂电池模型的精确辨识。

2) 使用RFEKF算法完成锂电池SOC估计，解决了EKF算法本身存在近似线性化误差问题，弥补了泰勒高阶余项。通过与标准EKF算法对比，结果表明，在相同工况下，使用RFEKF算法在初期、中期、后期都能够准确地估计SOC，更能接近真实值；其平均误差相较于标准EKF降低了32.8%，均方根误差降低了45.8%，数据表明使用RFEKF算法在复杂的工况中估计SOC有较强的鲁棒性和稳定性。

[1] 周维, 刘鸿远, 徐彪, 等.功率分流式混合动力矿用自卸车预测性等效燃油消耗最小控制策略研究[J].机械工程学报, 2021, 57(2): 200-209.

ZHOU Wei, LIU Hongyuan, XU Biao, et al.Predictive equivalent consumption minimization strategy for power split hybrid electric mining truck[J].Journal of Mechanical Engineering, 2021, 57(2): 200-209.

[2] 胡韵华, 冯瑾涛, 邓清闯, 等.电动汽车直流充电桩自动化测试平台的设计与应用[J].电力系统保护与控制, 2021, 49(7): 150-159.

HU Yunhua, FENG Jintao, DENG Qingchuang, et al.Development and application of automated test platform for DC charging piles of electric vehicles[J].Power System Protection and Control, 2021, 49(7): 150-159.

[3] 任怡睿, 林济铿, 宁剑, 等.一种基于占优度和Choquet积分的电力系统故障诊断方法综合评估策略[J].电力系统保护与控制, 2021, 49(6): 145-154.

REN Yirui, LIN Jikeng, NING Jian, et al.A comprehensive evaluation strategy of a power system fault diagnosis method based on dominance and the Choquet integral[J].Power System Protection and Control, 2021, 49(6): 145-154.

[4] YAN Gangui, LIU Dongyuan, LI Junhui, et al.A cost accounting method of the Li-ion battery energy storage system for frequency regulation considering the effect of life degradation[J].Protection and Control of Modern Power Systems, 2018, 3(1): 43-51.

[5] 明彤彤, 王凯, 田冬冬, 等.基于LSTM神经网络的锂离子电池荷电状态估算[J].广东电力, 2020, 33(3): 26-33.

MING Tongtong, WANG Kai, TIAN Dongdong, et al.Estimation on state of charge of lithium battery based on LSTM neural network[J].Guangdong Electric Power, 2020, 33(3): 26-33.

[6] 陈玉珊, 秦琳琳, 吴刚, 等.基于渐消记忆递推最小二乘法的电动汽车电池荷电状态在线估计[J].上海交通大学学报, 2020, 54(12): 1340-1346.

CHEN Yushan, QIN Linlin, WU Gang, et al.Online state of charge estimation for battery in electric vehicles based on forgetting factor recursive least squares[J].Journal of Shanghai Jiaotong University, 2020, 54(12): 1340-1346.

[7] RAHIMI-EICHI H, BARONTI F, CHOW M Y.Online adaptive parameter identification and state-of-charge estimation for lithium-polymer battery cells[J].IEEE Transactions on Industrial Electronics, 2014, 61(4): 2053-2061.

[8] 王志福, 刘兆健, 李仁杰.基于BCRLS-AEKF的锂离子电池荷电状态估计及硬件在环验证[J].北京理工大学学报, 2020, 40(3): 275-281.

WANG Zhifu, LIU Zhaojian, LI Renjie.State of charge estimation and hardware-in-loop verification of lithium-ion battery based on BCRLS-AEKF[J].Journal of Beijing Institute of Technology, 2020, 40(3): 275-281.

[9] 田晟, 吕清, 李亚飞.基于STEKF的锂离子动力电池SOC估算[J].华南理工大学学报(自然科学版), 2020, 48(2): 69-75.

TIAN Sheng, LÜ Qing, LI Yafei.SOC Estimation of li-ion power battery based on STEKF[J].Journal of South China University of Technology (Natural Science Edition), 2020, 48(2): 69-75.

[10] 康道新, 李立伟, 杨玉新, 等.基于DAUKF的锂电池SOC值和SOH值的估算研究[J].广东电力, 2020, 33(4): 9-16.

KANG Daoxin, LI Liwei, YANG Yuxin, et al.Estimation of SOC and SOH values of lithium battery based on DAUKF[J].Guangdong Electric Power, 2020, 33(4): 9-16.

[11] 缪家森, 成丽珉, 吕宏水.基于PSO-ELM的储能锂电池荷电状态估算[J].电力工程技术, 2020, 39(1): 165-169, 199.

MIAO Jiasen, CHENG Limin, LÜ Hongshui.Estimation of state of charge of energy storage lithium battery based on PSO-ELM[J].Electric Power Engineering Technology, 2020, 39(1): 165-169, 199.

[12] 寇发荣, 王思俊, 王甜甜, 等.VCM模型下的IBAS- EKF锂电池荷电状态估计[J/OL].机械科学与技术: 1-10[2021-05-09].https://doi.org/10.13433/j.cnki.1003- 8728.20200287.

KOU Farong, WANG Sijun, WANG Tiantian, et al.Estimation of IBAS-EKF lithium battery state of charge under VCM[J/OL].Mechanical Science and Technology for Aerospace Engineering: 1-10[2021-05-09].https://doi.org/10.13433/j.cnki.1003-8728.20200287.

[13] 刘芳, 马杰, 苏卫星, 等.基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J].电工技术学报, 2020, 35(4): 698-707.

LIU Fang, MA Jie, SU Weixing, et al.State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J].Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.

[14] 谈发明, 李秋烨, 赵俊杰.观测模型误差不确定的锂电池SOC估计方法[J].电测与仪表, 2020, 57(3): 32-38.

TAN Faming, LI Qiuye, ZHAO Junjie.Research on SOC estimation method for lithium batteries with uncertain model errors[J].Electrical Measurement & Instrumentation, 2020, 57(3): 32-38.

[15] 明彤彤, 赵晶, 王晓磊, 等.基于改进LSTM的脉冲大倍率工况下锂电池SOC估计[J].电力系统保护与控制, 2021, 49(8): 144-150.

MING Tongtong, ZHAO Jing, WANG Xiaolei, et al.SOC estimation of a lithium battery under high pulse rate condition based on improved LSTM[J].Power System Protection and Control, 2021, 49(8): 144-150.

[16]李军徽, 张晓驰, 李翠萍, 等.基于修正卡尔曼滤波SOC估算的锂电池变参数模型[J].热力发电, 2020, 49(8): 55-63.

LI Junhui, ZHANG Xiaochi, LI Cuiping, et al.Variable parameter model of lithium battery based on SOC estimation of modified Kalman filetr[J].Thermal Power Generation, 2020, 49(8): 55-63.

[17] 唐圣学, 邢玥, 张启然, 等.一种光伏电池动态模型的参数提取方法[J].电测与仪表, 2021, 58(6): 91-96.

TANG Shengxue, XING Yue, ZHANG Qiran, et al.Parameter extraction method of photovoltaic cell dynamic model[J].Electrical Measurement & Instrumentation, 2021, 58(6): 91-96.

[18]赵斌, 呼如威, 蒋东方, 等.高寒高海拔地区微网储能锂电池系统优化设计[J].中国电力, 2020, 53(5): 128-134.

ZHAO Bin, HU Ruwei, JIANG Dongfang, et al.Optimized design of lithium battery system for microgrid energy storage in severely cold and high elevation regions[J].Electric Power, 2020, 53(5): 128-134.

[19]简献忠, 武杰, 郭强.蜂群算法在太阳电池寿命预测参数辨识中的应用[J].太阳能学报, 2018, 39(12): 3392-3398.

JIAN Xianzhong, WU Jie, GUO Qiang.Application of artificial bee colony algorithm in parameter identification of solar cell life prediction[J].Acta Solar Energy, 2018, 39(12): 3392-3398.

[20] 蔡军, 邹鹏, 沈弼龙, 等.基于改进轮盘赌策略的反馈式模糊测试方法[J].四川大学学报(工程科学版), 2016, 48(2): 132-138.

CAI Jun, ZHOU Peng, SHEN Bilong, et al.Feedback fuzzing based on improved roulette wheel selection strategy[J].Journal of Sichuan University (Engineering Science Edition), 2016, 48(2): 132-138.

[21]王联国, 刘小娟.基于采蜜机制的正弦余弦算法及其在机械优化设计中的应用[J/OL].中国机械工程: 1-14 [2021-04-28].http://kns.cnki.net/kcms/detail/42.1294.TH.20210319.1738.018.html.

WANG Lianguo, LIU Xiaojuan.Sine cosine algorithm based on the honey gathering mechanism and its application in mechanical optimal design[J/OL].China Mechanical Engineering: 1-14[2021-04-28].http://kns.cnki.net/kcms/detail/42.1294.TH.20210319.1738.018.html.

[22] 张远进, 吴华伟, 叶从进.基于IFA-EKF的锂电池SOC估算[J].储能科学与技术, 2020, 9(1): 117-123.

ZHANG Yuanjin, WU Huawei, YE Congjin.Estimation of SOC of lithium batteries based on IFA-EKF[J].Energy Storage Science and Technology, 2020, 9(1): 117-123.

[23]高金辉, 朱迎正.基于新电源模型的动力锂电池荷电状态估计研究[J].河南师范大学学报(自然科学版), 2019, 47(1): 58-61, 92.

GAO Jinhui, ZHU Yingzheng.Study on state estimation of power lithium battery based on new power supply model[J].Journal of Henan Normal University (Natural Science Edition), 2019, 47(1): 58-61, 92.

[24] 刘兴涛, 李坤, 武骥, 等.基于EKF-SVM算法的动力电池SOC估计[J].汽车工程, 2020, 42(11): 1522-1528, 1544.

LIU Xingtao, LI Kun, WU Ji, et al.State of charge estimation for traction battery based on EKF-SVM algorithm[J].Automotive Engineering, 2020, 42(11): 1522-1528, 1544.

[25]李焱, 贾雅君, 李磊, 等.基于随机森林算法的短期电力负荷预测[J].电力系统保护与控制, 2020, 48(21): 117-124.

LI Yan, JIA Yajun, LI Lei, et al.Short term power load forecasting based on a stochastic forest algorithm[J].Power System Protection and Control, 2020, 48(21): 117-124.

[26] 程江洲, 谢诗雨, 张赟宁, 等.基于聚类加权随机森林的非侵入式负荷识别[J].智慧电力, 2020, 48(8): 123-129.

CHENG Jiangzhou, XIE Shiyu, ZHANG Yunning, et al.Non-invasive load identification based on clustering weighted random forest[J].Smart Power, 2020, 48(8): 123-129.

[27] LI Yi, ZOU Changfu, BERECIBAR M, et al.Random forest regression for online capacity estimation of lithium-ion batteries[J].Applied Energy, 2018, 232(15): 197-210.

[28] 于同伟, 丁岳, 李良, 等.用于就地化保护关键技术的SoC设计[J].电力系统保护与控制, 2019, 47(21): 150-155.

DING Tongwei, DING Yue, LI Liang, et al.SoC design for key technologies of outdoor installation protection[J].Power System Protection and Control, 2019, 47(21): 150-155.

[29] 江南雨, 武冬梅, 杜常清, 等.基于dSPACE的纯电动汽车整车HIL建模及测试[J].自动化与仪表, 2021, 36(3): 70-75.

JIANG Nanyu, WU Dongmei, DU Changqing, et al.HIL modeling and testing of pure electric vehicle based on DSPACE[J].Automation and Instrumentation, 2021, 36(3): 70-75.

[30] 步传宇, 姜昆, 任军, 等.基于改进型ASRCKF算法的锂离子电池荷电状态估计[J].广东电力, 2020, 33(10): 16-25.

BU Chuanyu, JIANG Kun, REN Jun, et al.Estimation of SOC of lithium-ion battery based on improved ASRCKF[J].Guangdong Electric Power, 2020, 33(10): 16-25.

Lithium battery SOC estimation based on an ABC-RFEKF algorithm

KOU Farong, WANG Tiantian, WANG Sijun, ZHANG Hong, MEN Hao

(School of Mechanical Engineering, Xi'an University of Science and Technology, Xi'an 710054, China)

Accurate and reliable state of charge (SOC) estimation can provide a guarantee for the safe and efficient use of battery management systems.Given that there is insufficient accuracy of SOC estimation of lithium batteries, this paper proposes the artificial bee colony algorithm (ABC) and the random forest optimized EKF algorithm (RFEKF) respectively to realize parameter identification and SOC estimation of the battery model.Based on the establishment of dualpolarization model, to solve the problem of the accumulation of initial errors in online identification, the ABC algorithm is used to search for the global optimal impedance parameter value under the minimum model voltage error, and realize accurate identification of model parameters.Based on obtaining accurate model parameters, this paper uses random forest (RF) to online compensate for the SOC posterior estimation error, and achieves the purpose of making up for the error of the high-order term of the traditional EKF algorithm.Then it achieves high-precision SOC estimation.Combining a hardware-in-the-loop simulation system and battery test platform, it realizes rapid control prototype verification for the SOC estimation algorithm under EPA urban power conditions.The results show that the error indicators of the lithium battery SOC estimation algorithm based on ABC-RFEKF are lower than the traditional SOC estimation algorithm.The average error is around 1%, thereby meeting actual engineering needs.This work is supported by the National Natural Science Foundation of China (No.51775426).

state of charge; artificial bee colony algorithm; random forest; extended Kalman filter; rapid control prototype

10.19783/j.cnki.pspc.210607

2021-05-20；

2021-07-05

寇发荣(1973—)，男，通信作者，博士，教授，主要从事车辆动力学以及电池管理系统方面的科研和教学工作；E-mail: koufarong@xust.edu.cn

王甜甜(1996—)，女，硕士研究生，主要从事电池管理系统方面的研究。E-mail: 1939027068@qq.com

国家自然科学基金项目资助(51775426)；陕西省重点研发计划项目资助(2020GY-128)

(编辑 周金梅)