基于车辆动力传动和转向系统的换道轨迹优化策略

廖鹏，唐铁桥*

(北京航空航天大学，a.交通科学与工程学院；b.车路协同与安全控制北京市重点实验室，北京100191)

0 引言

换道过程是驾驶员根据自身的驾驶习惯，综合考虑当前的交通信息(如换道车辆的位置、速度、加速度，以及换道车辆与周围车辆的位置差、速度差、加速度差等信息)，驾驶车辆由原始车道行驶到目标车道的复杂过程[1-2]。换道过程涉及到的环境复杂且交通因素较多，驾驶员通常需要多次修正其运行轨迹。因此，换道行为容易影响其周围车辆的行驶状态，并产生交通冲突，从而降低交通系统的安全性、经济性、舒适性和高效性。相关统计数据显示，由驾驶员引起的交通事故高达96.2%，其中由认知错误、决策错误和操作不当引起的事故分别占41%、33%和11%[3]。此外，美国公路安全管理局指出，换道引发的交通事故占所有事故的27%，其中驾驶员因素约占93%[4]。

现有换道轨迹研究主要包括换道轨迹规划和换道轨迹跟踪[5]。换道轨迹规划是获得换道轨迹的过程，保证换道轨迹具有连续曲率，同时满足运动学和动力学条件的约束。换道轨迹跟踪通过控制车辆动力传动系统和转向系统，实现预先规划的换道轨迹。基于特定几何曲线和优化计算的轨迹规划是最常用的轨迹规划方法。基于特定几何曲线的轨迹规划中，通常采用各种参数曲线(多项式曲线、圆曲线、贝塞尔曲线等)拟合换道轨迹点。任殿波等[6]基于多项式曲线构建了曲率可变的换道轨迹模型，以换道起始时刻和终止时刻的车辆状态以及换道时间标定多项式系数。Keller等[7]基于弹性带理论构造能量函数，以车辆动力学、道路边界和障碍物为约束，实现最优换道轨迹规划。比较常见的用于轨迹跟踪的控制算法有：最优预瞄控制、模型预测控制等。Park 等[8]考虑预瞄驾驶员模型，根据车速进行预瞄距离修正，实现了车辆转角控制。Golshan 等[9]采用模型预测控制算法对车辆的方向盘转角进行控制，实现了对避障轨迹的跟踪控制。上述对换道轨迹的研究，相对独立地研究换道轨迹规划和换道轨迹跟踪，从而无法避免两者之间产生的误差。随着自动驾驶技术和计算机技术的发展，基于车辆动力传动和转向系统的换道轨迹优化策略，可以通过优化动力传动和转向系统的控制变量来规划并实现换道轨迹，从而消除上述误差。

为提出符合驾驶员驾驶习惯的换道轨迹优化策略，本文通过NGSIM 数据获得驾驶员在换道过程中的主要驾驶任务，通过二自由度车辆模型刻画车辆的纵向和横向运动特性，结合驾驶员对车辆动力传动和转向系统的控制，构建结合换道轨迹规划和跟踪的换道轨迹优化策略，并根据不同目标函数选取对应的优化策略，在保证安全的前提下，实现换道的经济性、舒适性和高效性。本文能够科学指导换道轨迹的生成，为换道驾驶辅助系统提供理论依据和方法指导。

1 基于轨迹数据的换道任务

本文所用车辆轨迹数据源于NGSIM项目中的US101 公路的换道数据[10]。数据采集时间为2005年6月15日7:50-8:35，采集地点为US-101 公路中全长为630 m 的路段，其中包括5 个快车道(1～5 号车道)和一个辅道(6 号车道)，检测路段如图1所示。本文选取该数据集中所有换道车辆的纵向和横向位置、速度和加速度数据，分析换道的主要驾驶任务。

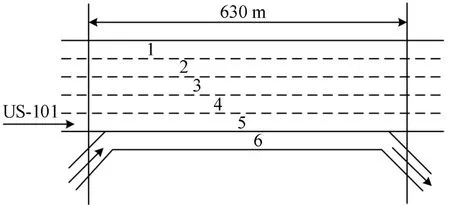
图1 US101公路检测路段Fig.1 Inspection section of US101 highway

1.1 数据预处理

由于NGSIM 数据并没有被过滤，故存在人为噪声。为了校正NGSIM 数据中的人为噪声，本文采用对指数移动平均法[11]对数据进行预处理。具体算法为

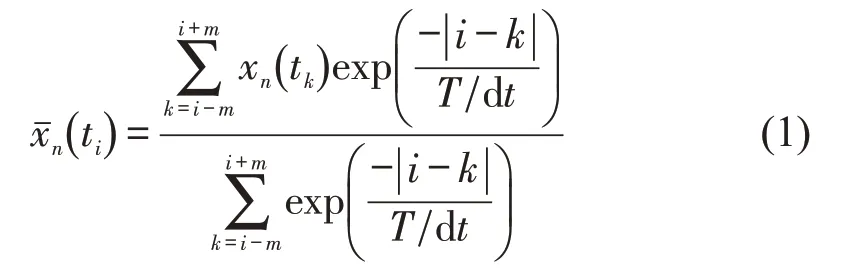
1.2 换道轨迹数据分析

在换道过程中驾驶员操控油门和方向盘来完成换道驾驶任务。在该过程中，驾驶员对油门的控制决定了车辆的加速度，而横向加速度则是由方向盘转角和车辆速度共同决定的。驾驶员执行车道保持任务和换道任务时，由于驾驶行为存在差异，导致车辆横向加速度变化有明显不同。当横向加速度呈现轻微的正负波动时，表示驾驶员在执行车道保持任务，这是因为驾驶员需要通过调整方向盘转角，消除车辆在行驶过程中产生的横向位移偏差。当横向加速度的方向在一段时间内保持相对不变，且车辆在这段时间内实现了对车道线的跨越，则可以认为该过程为换道过程。因此，根据车道和横向加速度的变化可以确定换道开始点、车道号变化点和换道结束点。换道开始点为车辆跨越车道线前，最近的一个横向加速度为0 m·s-2且上一时刻加速度方向与换道方向不同的点。车道号变化点可根据横向位置进行确定。换道结束点为车辆跨越车道线后，最近的一个横向加速度为0 m·s-2且下一时刻加速度方向与换道方向不同的点。选取换道开始点和换道结束点之间的数据进行分析。对比换道前后换道车辆的变化，可以确定换道的主要驾驶任务。

2 基于车辆动力传动和转向系统的动力学模型

驾驶员在换道过程中的控制体现在实时的纵向和横向位移变化。本节首先获得速度变化与动力传动系统控制变量的数值关系，再结合前轮转向轮(前轮)转角，确定实时的纵向和横向位移。

2.1 基于车辆动力传动系统的速度控制

内燃机车辆占据车辆保有量的97.7%，故本文以内燃机车辆的动力传动系统为例，求解车辆速度与动力传动系统控制变量的关系。内燃机的动力依次流经内燃机、无级变速器、其他传动装置和车轮。充分考虑动力传动系统的控制，内燃机车辆的动力学模型为

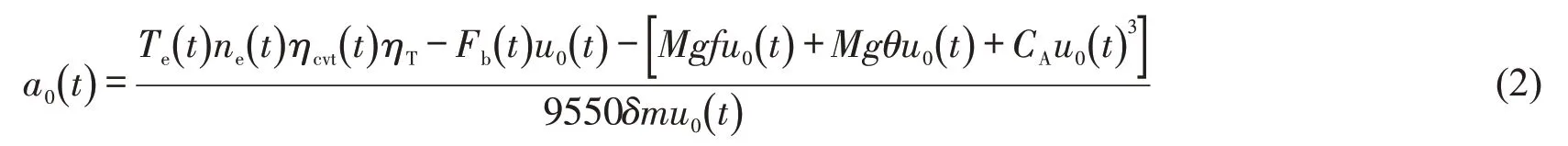
式中：a0为车辆加速度；u0为车辆速度；t为时刻；Te为内燃机转矩；ne为内燃机转速；ηcvt为无级变速器速比；ηT为其他传动装置效率；Fb为制动力；v0为车辆速度；M为整车质量；g为重力加速度；f为滚动阻力系数；θ为道路坡度；CA为空气阻力系数；δ为车辆旋转质量系数。

动力传动系统能够控制加速度的变化，从而产生速度变化。在此，将速度变化形式简化为“加速-匀速-减速”。并且为了提高计算速度，加速度的变化采用基于动力传动系统的燃油最优的加速、减速和匀速驾驶模式[12-13]。因此，对加速度的控制，由对内燃机转矩、内燃机转速和无级变速器速比的实时优化转化为对加速持续时间、匀速持续时间和减速持续时间的优化。于是，可以得到

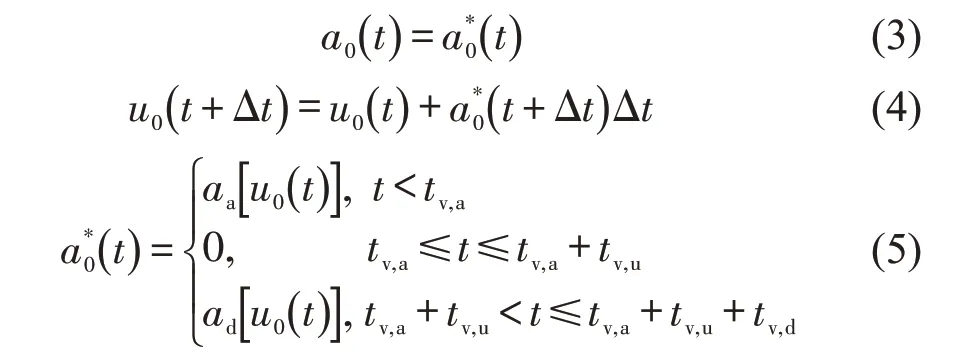
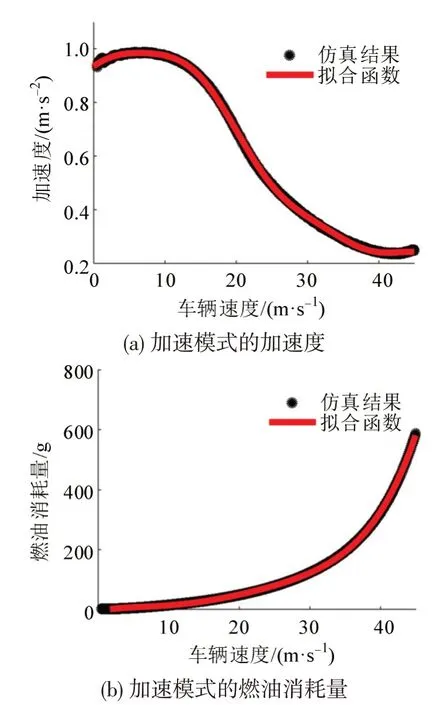
图2 加速模式的加速度和燃油消耗量Fig.2 Acceleration and fuel consumption in acceleration mode

图4 减速模式的加速度和燃油消耗量Fig.4 Acceleration and fuel consumption in deceleration mode

图3 匀速模式的每米燃油消耗量Fig.3 Per meter fuel consumption in uniform motion mode

2.2 基于车辆转向系统的位移计算

采用二自由度车辆模型作为参考模型[14]，求解不同车辆动力传动和转向系统控制变量下车辆的纵向位移和横向位移。将前轮作为转角轮，故该模型根据实时的前轮转角和速度变化，可以求出车辆的状态变化。其状态方程为

式中：β0为质心侧偏角；ω0为横摆角速度；δ0,f为前轮转角；Iz为整车绕铅垂轴转动惯量；kf，kr分别为前、后车轮等效侧偏刚度；lf，lr为整车质心至前、后轴距离；ulon,0为车辆纵向速度；ψ0为车辆速度与纵向方向的夹角。

在车辆行驶过程中，车辆在时间步的运动可以简化为匀速圆周运动，如图5所示。因此，结合二自由度车辆模型，可以获得车辆由t行驶到t+Δt时，所产生的纵向位移和横向位移为

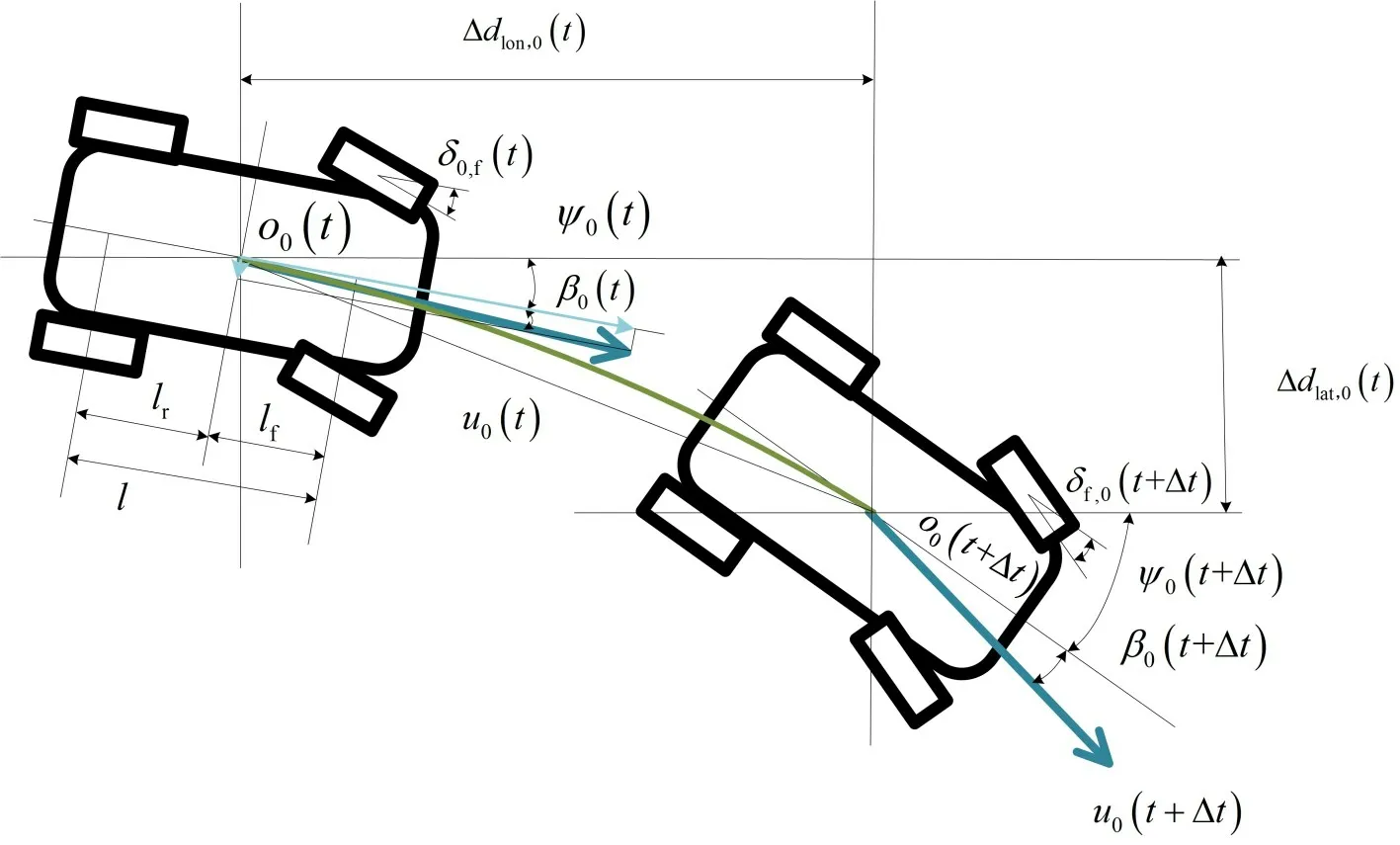
图5 基于二自由度车辆模型的纵向位移和横向示意图Fig.5 Schematic diagram of longitudinal and lateral displacement based on vehicle two-degree-of-freedom vehicle model

式中：Δdlon，0为车辆纵向位移；Δdlat，0为车辆横向位移。

前轮转角作为二自由度车辆模型的输入，与方向盘转角成正比，考虑驾驶员的具体操作情况，其变化形式简化为“0-增加-不变-减小-不变-增加-0”，并设其角速度的绝对值不变。由此将对前轮转角的优化，转化为对前轮转角的角速度、转角增加持续时间、转角不变持续时间和转角减小持续时间的优化。前轮转角的计算公式为

3 换道轨迹优化策略

换道轨迹的多样性是由驾驶员对油门和方向盘的控制变化产生的，实际上该变化是内燃机转矩、内燃机转速、无级变速器速比和前轮转角的变化。因此，优化策略需要根据换道驾驶任务，求解出动力传动和转向系统的控制变量。基于车辆动力传动和转向系统的动力学模型分析，将复杂的过程控制问题，转化为对加速持续时间、匀速持续时间、减速持续时间、前轮转角的角速度、转角增加持续时间、转角不变持续时间和转角减小持续时间的优化问题。所提的轨迹优化策略应该在保证换道安全的前提下，实现经济、舒适和高效的换道过程。因此该策略的目标函数为

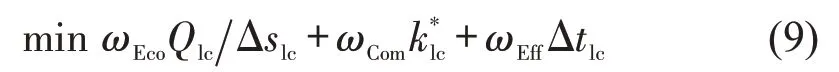
式中：ωEco为经济权重系数；Qlc为换道过程的燃油消耗量；Δslc为换道过程的行驶距离；ωCom为舒适权重系数；ωEff为高效权重系数；Δtlc为换道时间。

为了求解优化策略，需要引入对应的约束条件。选取不同的加速持续时间tv,a、匀速持续时间tv,u、减速持续时间tv,d、前轮转角的角速度k*lc、转角增加持续时间tang,a、转角不变持续时间tang,u和转角减小持续时间tang,d，就能获得结合轨迹规划和跟踪的换道轨迹，并计算出对应的燃油消耗量Qlc，前轮转角的角速度，换道时间Δtlc。为了保证求解速度，需要对优化变量进行取值约束，即

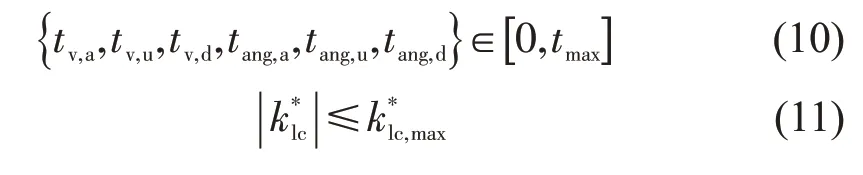
式中：tmax为最大持续时间；为最大的转向轮角速度。

为了保证动力传动和转向系统的安全运行，还需引入对应的安全约束，即

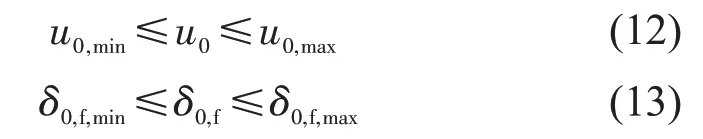
同时为了保证所提轨迹能够完成换道驾驶任务，需要引入对应的换道任务约束，即

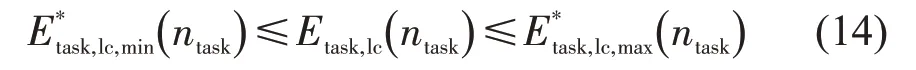
式中：u0,min为最小车辆速度；u0,max为最大车辆速度；δ0,f,min为最小前轮转角；δ0,f,max为最大前轮转角；为第ntask个换道驾驶任务的最小期望值；为第ntask个换道驾驶任务的最大期望值；为第ntask个换道驾驶任务的完成值。

通过确定的换道驾驶任务以及优化变量的不同取值，可以确定采用的加速度和采用的前轮转角的角速度。再结合约束条件，就可以根据目标函数，选取最优的换道轨迹。

4 结果与分析

4.1 基于NGSIM数据的换道驾驶任务

选取NGSIM 数据集中US-101 公路的所有换道数据进行分析，计算相关参数如表1所示。经过处理后，得到换道车辆及其周围车辆的位置数据，同时确定了换道车辆的换道开始点、车道号变化点和换道结束点。图2 为第12 辆车和周围车辆的轨迹，以及识别出的换道开始点、车道号变化点和换道结束点。由此说明所提的数据预处理能够很好地识别出换道轨迹及其关键点。

表1 计算相关参数Table 1 Calculation-relevant parameters

图6 第12辆车及其周围车辆的轨迹Fig.6 Trajectories of the 12th vehicle and its surrounding vehicles

通过对比换道车辆换道前后的差异，能够确定主要的换道驾驶任务。分别统计了换道时间、纵向位移、横向位移、纵向速度、横向速度、合位移和合速度这7个指标，得到它们的最大值、上四分位数、中位数、下四分位数、最小值和平均值，结果如表2所示。从这些统计值可以发现，主要换道任务是在一定时间内完成特定的位移以及速度变化，其中车辆运动状态的变化取决于车辆的纵向运动状态变化，即合位移和合速度的变化与纵向位移和纵向速度的变化保持高度一致。通过对换道驾驶任务的统计分析，充分考虑车辆所处的道路环境，以驾驶任务的最小值和最大值作为对应换道驾驶任务的最小和最大期望值。

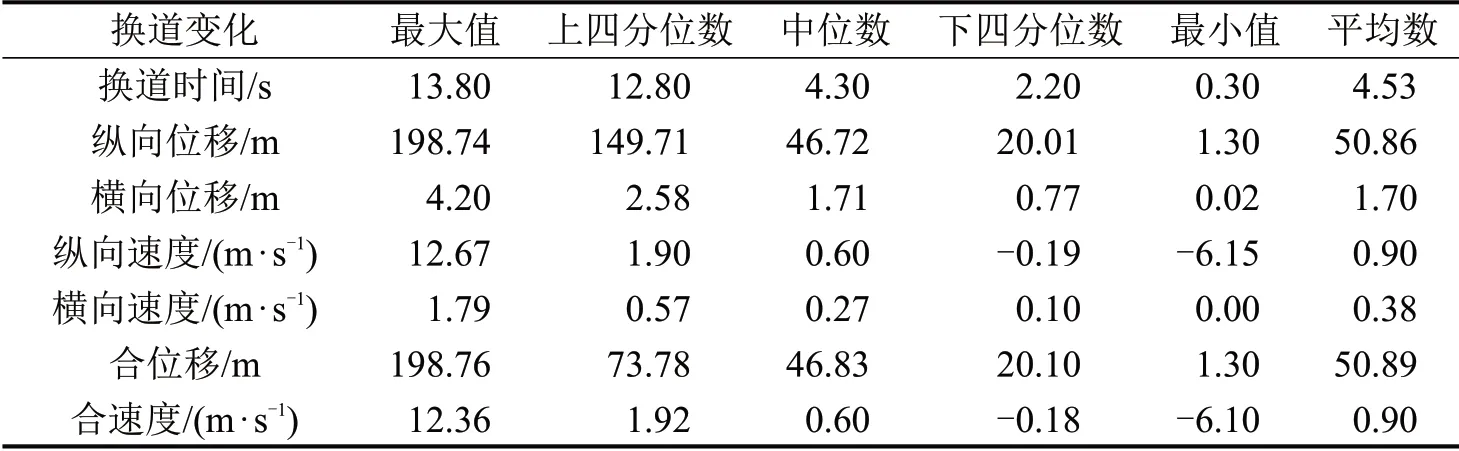
表2 NGSIM数据的换道前后差异Table 2 Difference before and after lane-changing from NGSIM data

为进一步验证所提驾驶任务的准确度，本文采用部分highD 数据[15]对其进行验证，得到的结果如表3所示。由于NGSIM 数据集和highD 数据集的换道平均速度分别为11.23 m·s-1和36.09 m·s-1，平均速度增大了221.37%，充分考虑到两个数据集的速度差异以及指标的多样性，本文对比两类数据的对应指标占比，并按NGSIM 数据占比从小到大展示结果，如图7所示。从图7可以发现，虽然两类数据之间存在差异，但换道过程中都存在位移和速度的变化，并且车辆运动状态的变化依旧取决于车辆的纵向运动状态变化。因此，期望换道驾驶任务的边界条件确定，应该充分考虑道路条件的变化。

图7 NGSIM数据和highD数据的换道前后差异对比Fig.7 Comparison of differences between NGSIM data and highD data before and after lane-changing

表3 highD数据的换道前后差异Table 3 Difference before and after lane-changing from highD data

4.2 原始轨迹与换道轨迹优化策略的性能对比

同样的以第12 辆车为例，仿真适用于该车的经济、舒适和高效的换道轨迹，并与实际轨迹进行对比。目标函数的权重系数依次设为和，用以求解经济、舒适和高效的换道轨迹。第12辆车的换道驾驶任务为在5.7 s内完成99.05 m的纵向位移，-2.73 m的横向位移，速度由18.33 m·s-1增加到18.79 m·s-1。为了更好地探究所提策略的性能，将第12 辆车的纵向位移和所需时间设为对应的最大期望换道驾驶任务，同时将最小期望换道驾驶任务设为0；将横向位移和速度变化的最小和最大期望换道驾驶任务分别设为第12 辆车的横向位移和横向速度变化的90%和110%。

图8 为原始换道轨迹与换道轨迹优化策略的纵向和横向位移对比，从中可以看出，经济轨迹与舒适轨迹高度重合，轨迹曲线完全重叠在了一起。它们充分利用了纵向空间来保证轨迹平缓，而高效轨迹则在较短的纵向位移内完成了换道过程。

图8 原始换道轨迹与换道轨迹优化策略的纵向和横向位移Fig.8 Longitudinal and lateral displacement of original lanechanging trajectory and lane-changing trajectory optimization strategy

图9 分别为各个轨迹的速度和加速度随时间的变化。值得注意的是，经济轨迹、舒适轨迹和高效轨迹相互重叠。所提策略具有较为平滑的变化，而原始轨迹则具有较为频繁的波动，这个差异是由加速度和前轮转角的角速度变化形式所决定的。结合表4可知，经济轨迹拥有最低的单位路程消耗燃油量，与高效轨迹的单位路程消耗燃油量相比，降低了35.71%。舒适轨迹的前轮转角的角速度达到了最小值，与经济和高效轨迹前轮转角的角速度相比，分别降低了79.31%和94.58%。高效轨迹所需时间达到了最小值，与原始、经济和舒适轨迹的所需时间相比，分别下降了70%，68.36%和64.93%。这说明所提的换道轨迹优化策略有广阔的选择空间，因为通过改变目标函数的权重系数能够对单位路程消耗燃油，前轮转角的角速度和所需时间进行进一步协调，实现不同的轨迹性能，以满足不同的驾驶需求。

图9 原始换道轨迹与换道轨迹优化策略的速度和加速度随时间的变化Fig.9 Variation of velocity and acceleration with time of original lane-changing trajectory and lane-changing trajectory optimization strategy

表4 原始轨迹与策略性能对比Table 4 Comparison between original trajectory and strategy performance

5 结论

本文通过NGSIM数据获得换道的主要驾驶任务。基于车辆动力传动和转向系统的动力学模型，探究了车辆速度与动力传动系统控制变量的数值关系，同时获得了车辆纵向和横向位移与动力传动和转向系统控制变量的数值关系。结合换道轨迹规划与跟踪，构建了换道轨迹的优化策略。结果表明，所提经济轨迹可以降低35.71%的单位路程燃油消耗，所提舒适轨迹能够降低94.58%的前轮转角的角速度，所提高效轨迹能够降低70%的换道所需时间。这说明所提优化策略有很大的应用潜力，并且通过调整优化策略的目标函数，能够找到满足驾驶需求的换道轨迹。基于车辆动力传动和转向系统的换道轨迹优化策略，不仅能够为驾驶员提供加速度和前轮转角的控制指示信息，而且能够通过控制动力传动和转向系统直接实现换道轨迹，从而消除轨迹规划与跟踪之间的误差。此优化策略丰富了换道轨迹的多样性，能够促进驾驶辅助系统的发展。在今后的研究中，将基于更详实的数据，探究驾驶员的换道偏好，并以此标定优化策略中的权重系数。同时，搭建合适的场景对策略进行验证，进一步提高策略的性能。