地表径流参数对洪峰流量和洪量的敏感性分析

刘兴峰

(新疆白杨河流域管理局，新疆 乌鲁木齐 830000)

城市洪水管理可以避免洪水对城市及其周边地区的负面影响[1-3]。峰值流量(Qp)和洪量(Vf)是城市洪水管理中最常用的两种参数输出[4]。研究表明，径流模型参数对两种参数有不同程度的影响。

本研究用计算选定径流模型参数，对洪峰流量(Qp)和洪量(Vf)的敏感性进行分析。通过强度频率持续时间模型分析设计降雨量，使用选定的雨水管理模型参数值模拟降雨径流模型，进行雨水管理模型参数对洪峰流量和洪量的敏感性分析。

1 模拟与方法

1.1 AusIFD的降雨量输入

AusIFD是一个免费软件，能够计算事件降雨强度及其分布模式。AusIFD是由昆士兰内森格里菲斯大学环境工程学院开发的。

使用AusIFD的第一步是从可用的指定地图中选择研究位置。一旦选择了ARIs，就可以确定平均降雨强度。降雨持续时间从5 min到72 h不等。计算的降雨强度以图表和表格的形式显示。

有四个合成降雨事件被计算作为进一步洪水模拟的输入。计算这些降雨强度所需的参数包括纬度、经度、偏斜度因子和区域因子，所有数据汇总于表1。

表1 计算研究区设计降雨量所需的参数

1.2 洪水模拟

洪水管理模型采用动态降雨径流模型模拟城市径流的数量和质量。此外，SWMM模拟了城市水文和水质的各个方面，诸如：降雨、降雪、径流、排水和蓄水等循环。SWMM可用于连续模拟或单一事件模拟。

SWMM中的水文循环要素可以用多种技术计算。例如，渗透可以用格林安普特法、霍顿法或SCS法计算。蒸发率可以表示为常数。降雨通过三个参数描述的单位过程线转化为径流，即进入研究区域的降雨部分(R)、到达峰值的时间(t)和衰退时间与到达峰值的时间之比(k)。

径流路径采用非线性水库路径技术，上游降雨是土壤水分运动的主要输入，而输出包括入渗、径流和蒸发。集水径流面积可以通过从最大洼地蓄水量(dp)中减去径流深度来计算。

在SWMM中，地下水成分在两个区域建模。第一个区域是不饱和的，土壤湿度用θ表示，而第二个区域是饱和的，位于第一个区域之下，土壤孔隙度用φ表示，计算了入渗、蒸散、渗流和侧向流，就可以推导出每个区域地下水储量变化的质量平衡方程，地下水平衡方程的计算以迭代方式求解。

本文分别采用霍顿法和运动波法计算入渗和洪水演进，时间间隔为15 s。假设降雨集中在研究区域的中心，然后进入排水交汇处。径流随后流入封闭的管道，管道呈圆形，直径为1 m，粗糙度为0.01，最终汇集在排水口。表2显示了工程中使用的接头和导管标准。

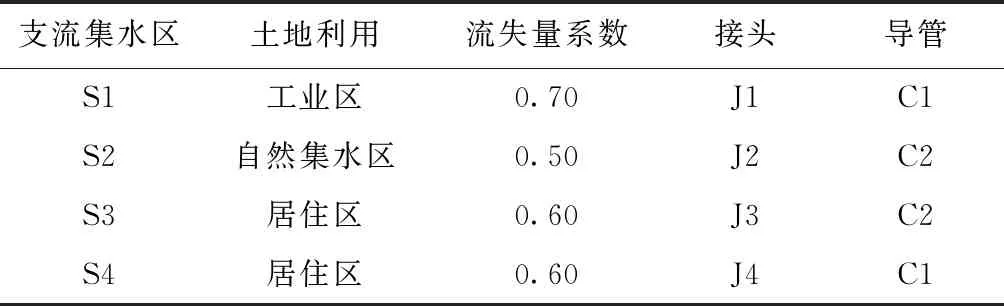
表2 工程中使用的接头和导管标准

1.3 灵敏度分析

采用流域附近住宅区的10个历史降雨数据，校准并验证了两个降雨径流模型参数，即透水洼地蓄水量和不透水率。研究表明，降雨深度对这两个参数最敏感，对空间概念最不敏感。

研究区域的集水区由居住区、自然集水区和工业区组成。利用Box优化算法，基于10次降雨事件进行了校准和验证，选取了集水区不透水性、集水区宽度、透水洼地蓄水系数和曼宁系数四个参数。根据灵敏度分析的目标寻求改变参数值对期望输出的影响。例如，不透水百分比和洼地蓄水对洪峰流量和洪量的影响最大，而曼宁系数的影响最小。

另一项研究旨在确定需要以最高精度估计的参数，因为该参数对期望的输出具有最重要的影响。根据水处理设备的总成本评估了四个成本计算参数的敏感性。首先找到最佳参数值，然后在保持其他三个参数不变的情况下，每次将参数值减少25%，重复上述过程。接下来参数值每次增加25%,同时保持其他三个参数不变。计算每个场景的总成本，并相互比较。得出的结论是，总成本对幂系数函数最敏感，其次是函数幂、利率和时间尺度。

默认参数值首先被输入到SWMM中，在低估情况下，默认参数值减少了25%，而在高估情况下，默认参数值增加了25%。在这两种情况下，一次减少或增加一个参数，而其他参数值保持不变。

2 模拟结果

2.1 设计降雨强度

根据表1给出的参数显示，可以计算30 min的设计降雨强度。这里评估了两组降雨强度，即第一组为2年平均降雨量，持续12 h，第二组为50年平均降雨量，持续72 h。表3给出了30 min内设计降雨强度的分布。

2.2 洪水模拟

表4显示默认参数值的峰值流量和洪峰，默认参数值基于编写的SWMM手册。

表5和表6分别给出了低估情景和高估情景下的洪峰流量和洪量。

为了评估参数对洪水模拟输出的敏感性，将表5和表6中的结果与表4中的结果进行了比较。低估情景和高估情景与使用默认参数值的情景之间的洪峰流量Qp和洪量Vf差异分别见表7和表8。

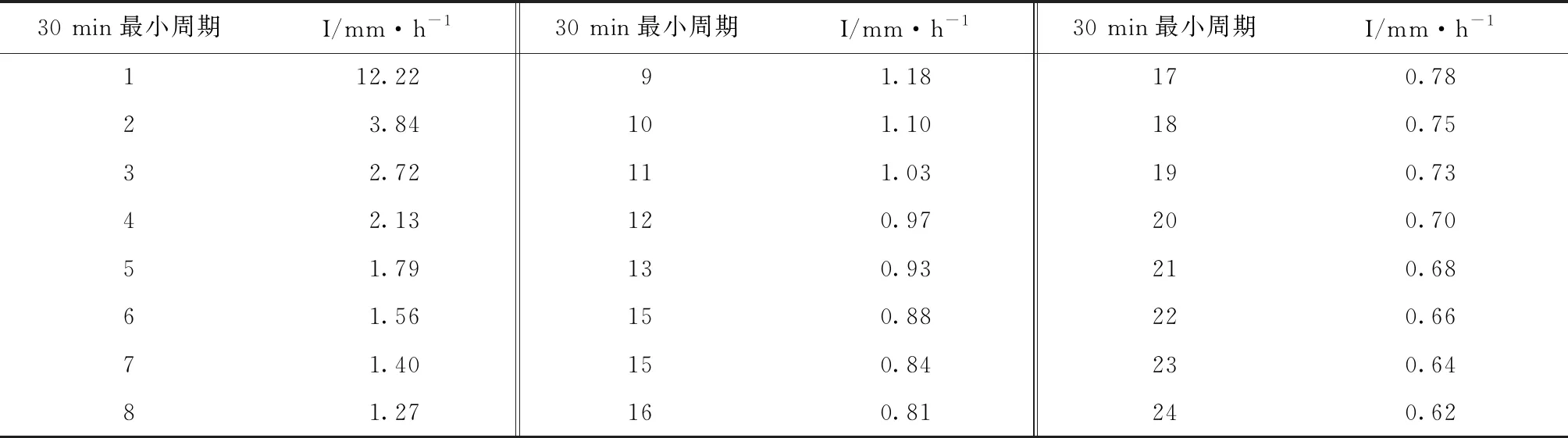
表3 2 a ARI、12 h持续时间的设计降雨强度分布

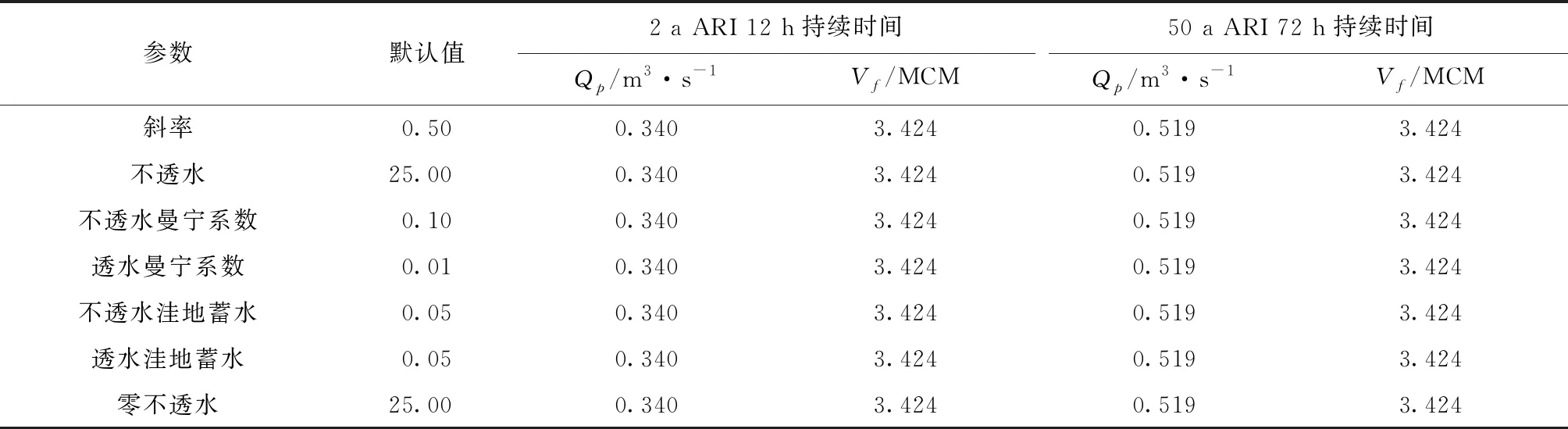
表4 默认参数值的峰值流量和洪量

表5 低估情况下的洪峰流量和洪量

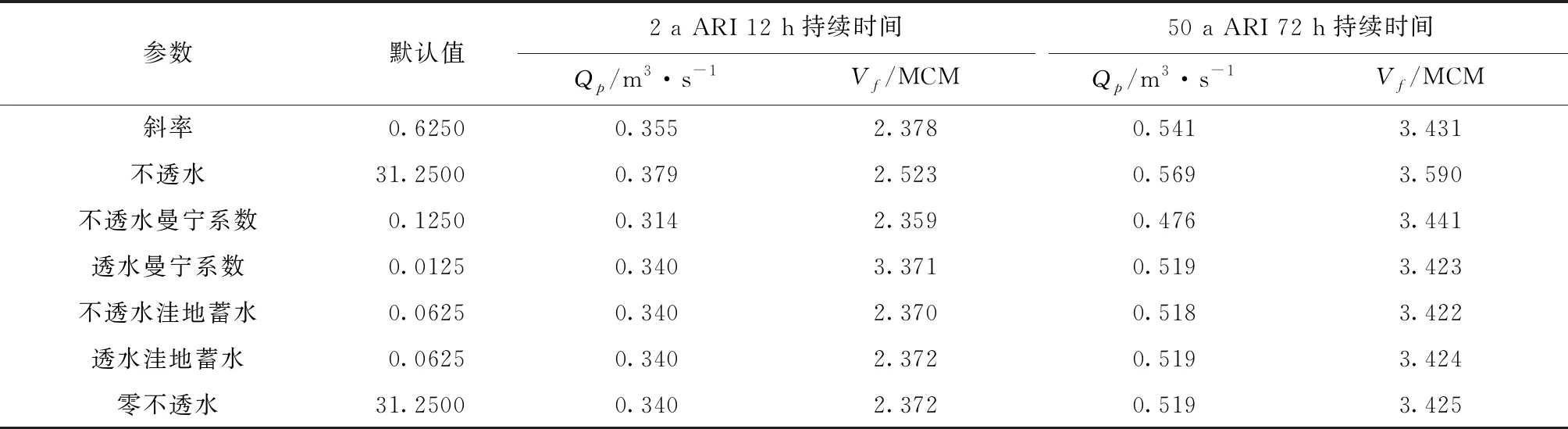
表6 高估情况下的洪峰流量和洪量

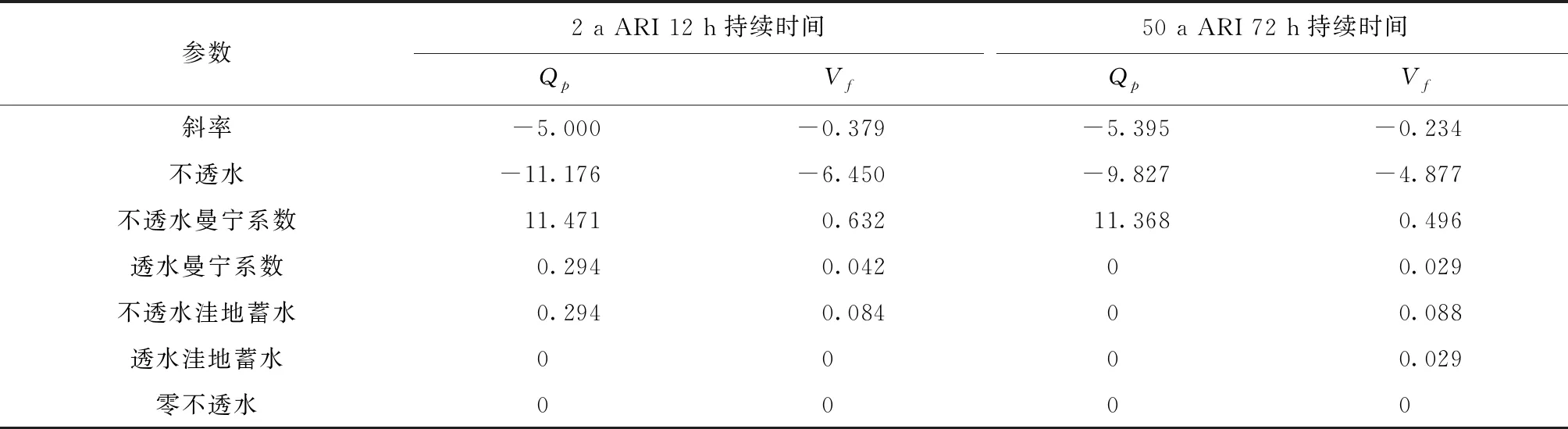
表7 使用默认参数值和低估方案之间的差异 %

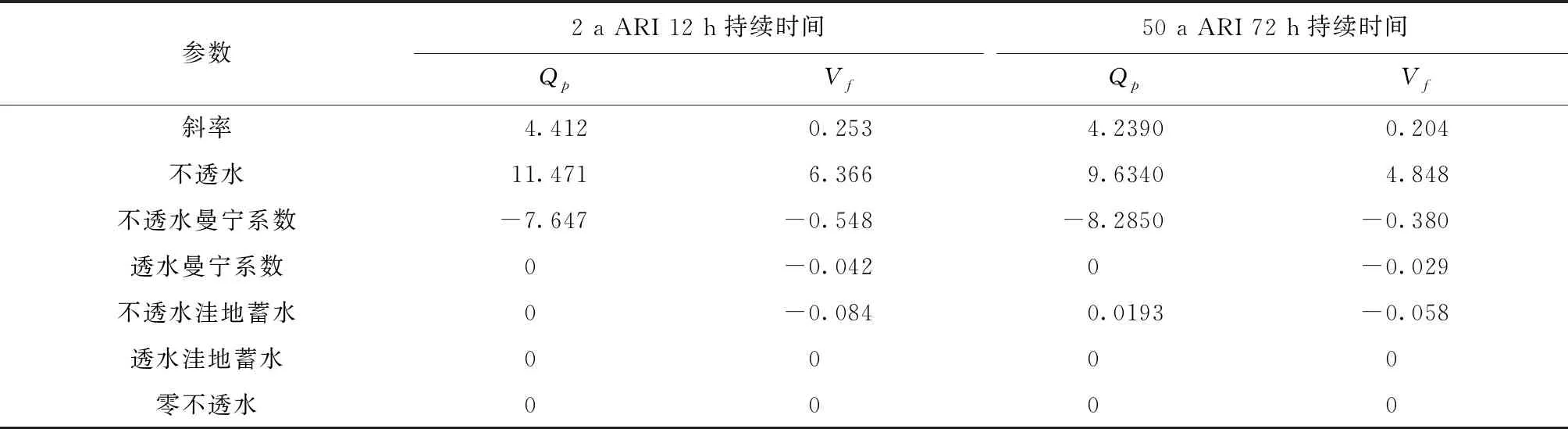
表8 使用默认参数值和高估方案之间的差异 %

3 结 论

城市洪水管理中最受关注的两个模型输出是洪峰流量(Qp)和洪量(Vf)。这些输出可以通过更好地理解选定的城市洪水模型参数来管理，其中最敏感的参数可以通过敏感性分析来分类。

郊区的一部分被选为研究区域，两个设计降雨强度作为SWMM模型的输入。第一套是2 a 12 h的降雨强度，第二套是50 a ARI 72 h的降雨强度。三个参数集被输入到SWMM模型中，以计算出流量(Qp)和洪量(Vf)对参数最敏感及最不敏感性。在第一次建模中，所有参数都被设置为各自的默认值，而在第二次和第三次建模中，所有参数分别被设置为比默认值小25%(低估情况)和比默认值大25%(高估情况)。

在2 a ARI 12 h持续时间设计降雨强度为输入的低估中，两个参数，即不透水性曼宁系数和透水性曼宁系数被证明是计算洪峰流量Qp和流量Vf的最重要参数。将防渗层减少其默认值的25%会使洪峰流量Qp减11.176%，而对曼宁的透水层产生的洪峰流量Qp也是如此，该洪峰流量Qp比使用默认值时大11.471%。洪水量只对曼宁透水率敏感，减少了6.45%。与此同时，通过输入50 a ARI 72 h事件持续时间，降雨强度通过降低不透水率将洪峰流量Qp降低了9.827%，并通过降低曼宁透水率将洪峰流量Qp乘以11.368%。洪量Vf仅对不透水敏感，减少4.877%。

在2 a ARI持续时间为12 h的事件降雨强度的高估情景在计算Qp时显示了类似的结果。不透水率降低25%会导致洪峰流量Qp降低11.471%，而曼宁不透水率降低7.647%。通过增加6.366%的洪水量，曼宁透水率是预测洪水量的唯一重要参数。在50 a 72 h事件中，降低防渗和曼宁透水分别产生了9.634%的较低洪峰流量Qp和8.285%的较高洪峰流量Qp。仅不透水也是预测洪水量的关键，减少了4.848%。