基于反卷积波束形成算法的干式变压器异响故障识别技术

包海龙，邵宇鹰，王枭，彭鹏，袁国刚，庄贝妮

(1. 国网上海市电力公司，上海 200122；2. 上海睿深电子科技有限公司，上海 201108)

0 引言

干式变压器异响问题一直是变压器状态检测领域研究的热点和难点。在实际工作中，干式变压器异响检测主要采用声压计检测法、声信号检测法及振动检测法。声压计检测法是由传声器将声音信号转换成电信号，再通过前置放大器将电信号进行频率计权，然后经衰减器、放大器将信号放大到一定的幅值，送到有效值检波器，得到声信号的数值，该方法主要用来衡量变压器的噪声水平；声信号检测法是通过检测声信号的音色、音量、频谱分布等物理特征判断变压器的运行状态，与声压计检测法相比，该方法可获得更多的变压器物理信息，因而得到较多关注，该方法的核心技术之一是声信号处理方法，先后出现了Hilbert-Huang变换法、Mel倒谱系数法以及基于稀疏表示理论的稀疏分量分析法等[1-4]；振动检测法是在变压器表面放置多个振动传感器，通过检测变压器机械振动特性变换特征，判断变压器运行状态。与前面2种方法相比，该方法优点是灵敏度高，可确定振动源位置，缺点是需要在变压器表面布置多个有线传感器，操作较烦琐，振动信号分析方法主要有小波分析法、神经网络法、系统聚类分析法等[5-8]。

另一方面，声学定位技术近年来逐渐受到研究者广泛关注，通过计算声信号到达多个声学传感器的时间差或相位差进行声源定位的方法。以往声学定位技术主要应用于海底探测、汽车制造、发动机故障识别、国防军事等领域[9-10]。近年来，随着中国电力设备数量不断增多，负荷逐渐增大，电力设备故障频发，有研究者将声学定位技术用于电力设备故障定位的研究，文献[11]将基于波束形成方法的声学定位技术应用到±800 kV换流站噪声源识别，研究结果发现电抗器组区域噪声在562～708 Hz存在较明显峰值，站用变区域最大噪声点为变压器本体，频谱主要分布在 100 Hz及其倍频上，以 291～375 Hz频率分量较大；文献[12]将振动方法与声学定位技术相结合，研究了基于声纹及振动的变压器故障诊断方法，成功定位了一台110 kV油浸式变压器异响所在位置。

上述研究对象均是高电压等级敞开式电力设备或大型油浸式变压器，与这类设备相比，干式变压器体积较小，且多数安装于室内封闭空间，极易出现空间回声，干式变压器附近设备运行时产生的噪声干扰更加严重。如果仍将传统波束形成算法直接用于干式变压器异响故障定位，极易导致定位区域过大，影响判断的精度和准确性，甚至无法定位缺陷位置。因而，需要提高声学定位装置的定位精度和抗干扰能力，提升声学定位技术应用于干式变压器缺陷或故障定位的适用性。

本文首先分析了波束形成算法的基本原理，然后研究了一种基于反卷积变换的改进波束形成算法，提出了一种采用异响精准定位联合声纹图谱特征识别的干式变压器故障识别方法，最后通过对某在运干式变压器异响位置的判定和故障类型的识别，验证方法的有效性和准确性。

1 常规波束形成算法

波束形成算法是一种典型的声源定位算法，常规波束形成（conventional beamforming CBF）属于多通道声学传感器阵列语音增强技术中的抑制噪声类方法。其原理是阵列中各声学传感器单元接收的声音信号按聚焦点进行加权求和输出，再通过计算聚焦面上对应网格点的阵列输出最大值，确定声源的位置[13-14]。其中，常规波束形成中的互谱成像波束形成算法原理如图1所示，设M个声学传感器“●”组成的检测阵列在xoy面上，假设目标声源点为单极子声源点，rm（m=1,2,···,M）是m号声的位置，声阵列与聚焦面距离为d，将聚焦面沿x，y轴方向平均分成S个聚焦点。

图1 波束形成技术目标声源定位示意Fig. 1 Schematic diagram of beamforming positioning technology

2 基于反卷积变换的波束形成算法

由于声学传感器阵列采样的离散性和有限性，常规波束形成算法输出结果通常会出现主瓣宽度大、旁瓣数量多的现象，从而造成目标声源定位精度差[16]。为了提高波束形成算法的目标声源定位准确率，文献[17-20]提出反卷积DAMAS算法，即利用波束形成算法输出结果、声源分布及 p sf函数之间的卷积关系建立线性方程组，以矩阵形式表达为

具体算法流程如图2所示，图2中计算阵列各传感器接收的声学信号完成后，黑色虚线流程为常规波束形成算法成像目标声源，红色实线流程为基于反卷积变换的波束形成算法成像目标声源，该算法消除了实际应用中波束形成算法出现主瓣宽度大、旁瓣数量多的现象，有效的衰减了旁瓣水平与减小了主瓣宽度，继而提高目标声源定位结果的精度，此外还提高了计算效率，因而该算法适合用于类似干式变压器故障识别等需要精准定位的应用领域。

图2 两种算法对比流程Fig. 2 The flow chart of different algorithms

3 试验方案及装置

试验实体布置如图3所示，试验中的检测装置为由112个声学传感器组成的传感器阵列声学采集定位系统，其直径为0.78 m，传感器阵列放置于干式变压器正面，距离其1 m的位置。该系统可实时将采集到的声学信息和图像数据传输到分析软件，得到传声器信号的互功率谱矩阵，最后利用上述方法计算得到被检干式变压器的声源图像，判别故障位置和声信号信息。

图3 实验整体布置Fig. 3 Experiment layout diagram

该变压器为一台已退役的三相环氧浇注式干式变压器，电压等级为 10 kV，容量为 800 kV·A，其他参数如表1所示。该型号干式变压器在配电网中较为常见，具有较强的代表性。实验中，使用铜板将干式变压器一次侧高压端短接，380 V电源作为输入电源，每次在变压器本体缺陷设置完成后，通过升压变压器，对干式变压器二次低压侧由零逐步升压至额定电压，达到额定电压后保持稳态运行，再开启声学定位装置进行检测。其中，声学传感器采样频率为48 kHz，单次信号采集时长为10 s。

表1 实验用干式变压器参数表Table 1 The parameter of dry-type transformer in the experiment

4 试验结果分析

在干式变压器未设置任何缺陷，正常运行情况下，两种算法的定位结果如图4所示。其中，图4a）为常规波束形成算法得到的定位结果，图4b）为上文分析的基于反卷积变换波束形成算法得到的定位结果。可以看出，常规波束形成算法得到的定位结果，显示的定位区域大，几乎覆盖了变压器2/5的面积区域，包含了变压器铁芯、螺栓、线圈等容易出现异响的部件，中心位置定位精度差，无法分辨异响准确位置；而基于反卷积变换的波束形成算法得到的定位结果，显示的定位区域小，不及变压器1/10的面积区域，且可以分辨出两个声源点，中心位置定位精度更高，可准确显示干式变压器定位区域特征。

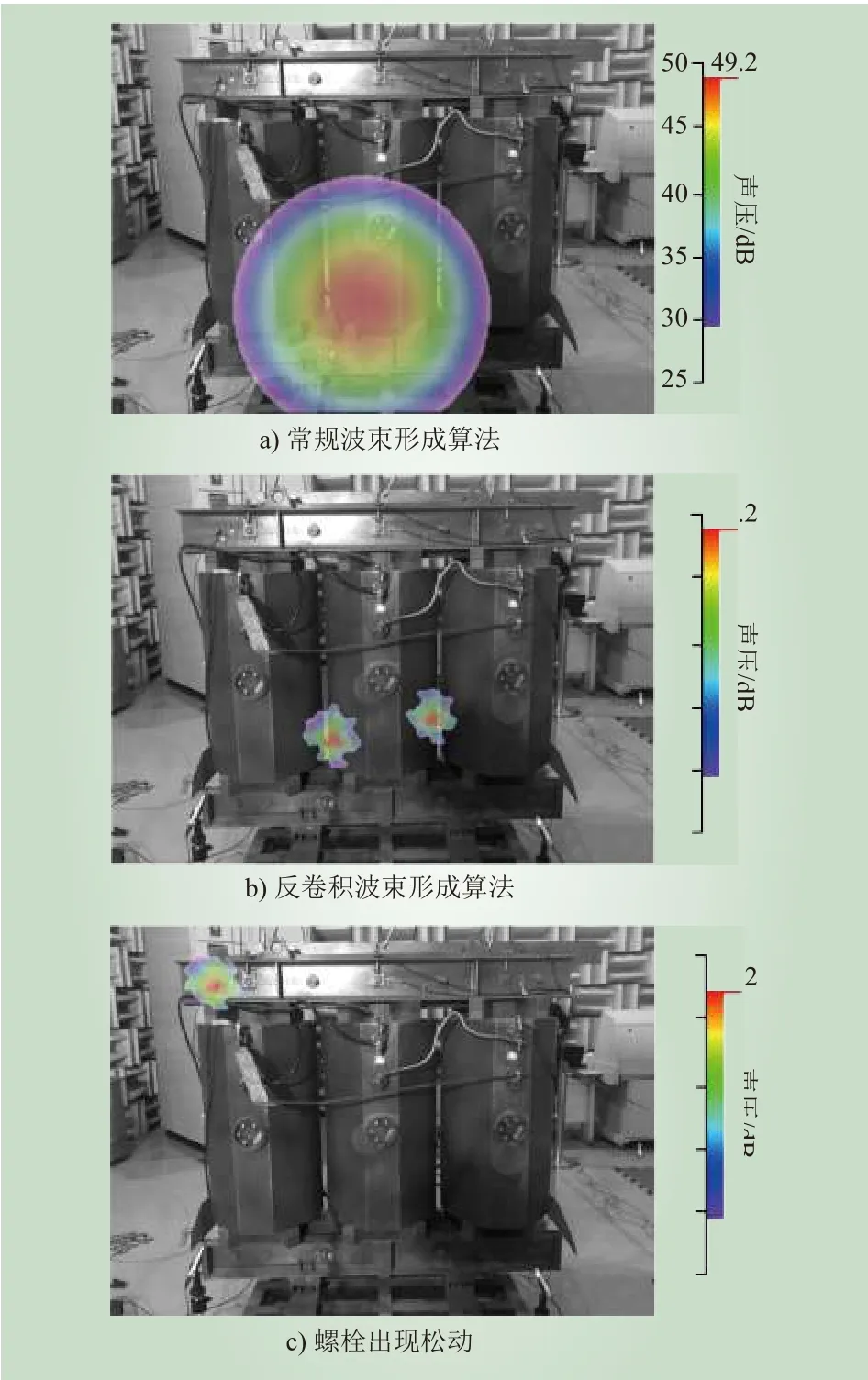
图4 不同运行状态及定位算法下的声学成像Fig. 4 The acoustic image of a dry-type transformer with different running status and algorithm

对应图4、图5黑线和蓝线分别为2种定位算法下的声学信号频谱图，可以看出两种算法下测得的频谱图差别不大。正常运行的干式变压器，主要特征频率峰为 100 Hz、200 Hz 以及 300 Hz，两种算法测得的声学信号频谱图基本相同，最大值为45.7 dB，均出现在100 Hz附近，这说明两种算法只影响定位空间准确性，对声学信号的图谱特征基本没有影响。

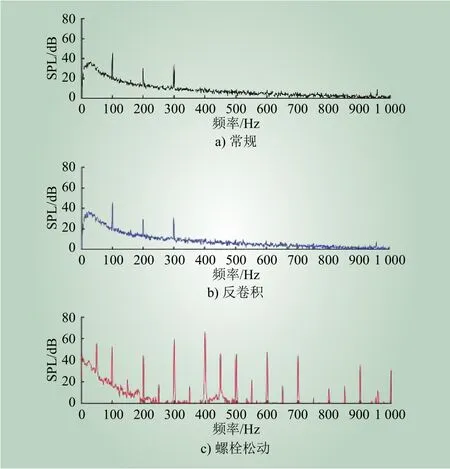
图5 干式变压器在不同运行状态下的声学频谱Fig. 5 The acoustic spectrum diagram of a dry-type transformer with different running status

为进一步研究干式变压器出现机械振动时的定位准确性和频率图谱特征，在变压器本体上将铁芯上部第一颗螺栓朝着松动方向旋转，使其螺栓紧固力矩为最大紧固力矩的20%，以模拟变压器长期运行后，某颗螺栓出现松动的情况，其他螺栓保持正常状态不变。对应的定位结果如图4c）所示，可以看出，基于反卷积变换的波束形成定位方法可以精准定位缺陷位置，定位中心区域即为被松动螺栓所在位置。此时的声学图谱如图5红线所示，可以发现，与干式变压器正常运行时相比，此时频谱信号信息更为丰富，100 Hz、200 Hz以及300 Hz等低频特征频率峰值更强，出现了 400 Hz、500 Hz、600 Hz、700 Hz 等高频特征峰，400 Hz特征峰强度最大，为63.5 dB。值得注意的是，螺栓松动时出现了大量50 Hz奇数倍频分量，这是由于螺栓出现松动后，螺栓在电磁力的作用下与变压器本体碰撞更为剧烈，400 Hz及以上高频分量、50 Hz奇数倍频分量迅速增强，激发的声信号经空气传播，最后被声学传感器阵列捕获。与通常单麦克风测量得到的声信号相比，传感器阵列由数十个声学传感器组成，所测信号更为准确，提高异响定位精确性的同时，也提升了异响频谱的准确性。

为分析不同机械振动强度下，基于反卷积变换波束形成算法定位的有效性和异响信号的图谱特征，本文研究了不同紧固力矩情况对应的检测效果，如图6和图7所示。可以看出，随着紧固力矩的增大，各频段声音强度均有所降低。其中，400 Hz、500 Hz、600 Hz、700 Hz 等高频特征峰逐渐下降，而 100 Hz、200 Hz 以及 300 Hz 等低频特征频率峰值下降较微弱。50 Hz奇数倍频分量特征峰也随着紧固力矩的增大而逐渐减弱，直至消失。当力矩增加到100%紧固力矩定值时，机械振动引发的异响消失，图谱特征与图5黑色实线相似，定位区域与图4b）正常运行时几乎一致，干式变压器恢复正常运行。应该强调的是，在螺栓被紧固的过程中，异响定位影像区域点始终在松动螺栓所在位置，这说明本方法可以用在干式变压器机械振动异响检测，且具有较高的精确性和稳定性。

图6 干式变压器在不同紧固力矩下的声学成像Fig. 6 The acoustic image of a dry-type transformer with different tightening moments

图7 干式变压器在不同紧固力矩下的声学频谱Fig. 7 The acoustic spectrum diagram of a dry-type transformer with different tightening moments

为量化干式变压器异响特征，有效评价机械振动引发异响的严重程度，本文定义了高频特征峰能量比S，以表征高频特征值峰能量的总能量占比，其表达式为

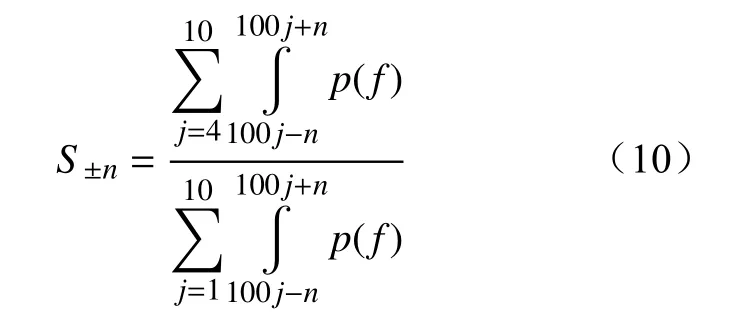
式中：声强p为频率f的函数，表征不同频段对应的声音强度；n为小频率变化量，可取1 Hz、3 Hz、5 Hz、10 Hz 等值。S±n可称为±nHz 高频特征峰能量比。

对应图5不同运行条件下声学图谱，根据式（10）计算得到不同运行条件下的高频特征峰能量比S，如表2所示。可以看出，干式变压器正常运行状态下，高频特征峰能量比S随着小频率变化量n的增大而增大；干式变压器出现机械异响状态下，高频特征峰能量比S随着小频率变化量n的增大而减小；而对于相同的n，机械异响状态下与正常运行状态下S值的变化量，随着n的增大而减小。显然，变化量越大，检测灵敏度越高，但为了统一不同检测装置分辨率差异可能引起的误差，小频率变化量n取声学图谱特征峰半峰宽（w）的1/2作为参数定值，将半峰宽高频特征峰能量比Sw/2作为定量表征机械异响严重程度的特征量。对于实验中所用干式变压器，正常运行时Sw/2=0.2745，图5对应的出现机械异响状态时，Sw/2=0.6579。

表2 不同运行状态和n值对S的影响Table 2 The influence of different tightening moments and the non S

5 现场测试与分析

某变电站运维人员发现，一在运干式变压器出现异响，采用本文方法对其异响定位，分析声学图谱特征，检测结果如图8所示，可以看出，异响声源点位于干式变压器上部，异响幅值为70.6 dB，远高于正常运行时的声学强度，对应的特征频谱如图9b）所示，图9a）为该干式变压器正常运行时的特征频谱曲线。从图中可以发现，与正常运行时不同，异响时声学图谱中出现了400 Hz、500 Hz、600 Hz 等高频特征分量，以及50 Hz奇数倍频特征峰。再根据式（10），计算得到半峰宽高频特征峰能量比Sw/2=0.6441，与图5对应的出现机械异响状态时Sw/2的特征值（0.6579）接近。根据上文的分析，该干式变压器具有典型机械异常振动引发异响的特征。停电检修后发现，定位所在位置螺栓松动，紧固后重新带电运行，异响消失，干式变压器恢复正常运行，避免了螺栓继续松动可能引发的故障。

图8 某在运干式变压器出现异响时的声学成像Fig. 8 The acoustic image of a running dry-type transformer with abnormal noise

图9 在运干式变压器在不同状态下的声学频谱Fig. 9 The acoustic spectrum diagram of a dry-type transformer with different running status

6 结语

本文将基于反卷积波束形成算法的用于干式变压器异响故障识别。首先具体分析了该算法的基本原理和先进性，通过实验验证了该方法比常规波束形成算法定位精度更高；然后研究了干式变压器出现机械异响时定位准确性，提出采用异响精准定位联合声纹图谱特征识别的干式变压器故障识别方法，提出了“高频特征峰能量比”的概念，用于量化机械异响严重程度；最后通过对某在运干式变压器异响位置的确定和故障类型的识别，验证了方法的有效性和准确性。