储能电站安全参与电网一次调频的优化控制策略
2022-03-02张嘉诚夏向阳邓子豪陈贵全
张嘉诚,夏向阳,邓子豪,陈贵全
(长沙理工大学 电气与信息工程学院,湖南 长沙 410114)
0 引言
随着社会经济的发展,风力、光伏等新能源技术快速发展[1-2],大规模储能系统因其配置灵活、响应速度快,能够较好地保证新能源供电的平衡性和连续性[3-5]。储能技术作为智能电网领域中关键的组成部分,其发挥的作用越来越重要[6-8]。国家以及地方关于储能方面的政策频频出台,并且发展储能有效带动了地方经济增长,储能技术迎来了高速发展期[9]。为了保证电网在不同扰动下的安全稳定,大规模储能在电网调频中的应用是当今研究热点[10-14]。
目前,国内外学者对参与电网一次调频的储能电站控制策略进行了大量研究。文献[15]建立了符合调频需求的储能电池模型,提出储能调频输出功率调节模式,并体现了相比传统机组的优势。文献[16]在下垂控制中采用恒定的下垂系数 ,没有考虑电池荷电状 态 ( state of charge,SOC)对储能输出功率的影响。当前针对大规模储能电站辅助电网调频的研究多采用定系数法,连续负荷扰动可能使储能单元产生过充过放现象,进而发生不可控安全事故,考虑经济性,当前电池储能成本较高,对电池控制不当会影响储能系统长时间可持续发展。文献[17-18]均考虑到电池SOC,分别提出变系数下垂控制与自适应下垂控制,更好地调整电池出力。文献[19]为缓解扰动初期频率恶化程度,新增虚拟惯性控制,但配合下垂控制仅设置时间延迟,一次调频效果略有不足。现有研究都是将储能系统看作一个整体进行能量调度,没有考虑健康状态(state of health,SOH)对电池充放电的影响,缺少对储能系统内部结构的考虑,而实际工程中储能电站是由多组电池簇并联组成。
综上所述,本文充分考虑电池储能结构特点及关键状态参数,针对当前储能电站参与电网一次调频的不足,提出一种考虑储能单元SOC、SOH及多储能单元组优先投切问题并融合虚拟惯性和可变下垂控制的综合控制策略,在传统虚拟惯性控制基础上引入健康因子,根据SOH调整出力深度;在估计电池SOC、SOH的同时,引入储能单元组优先投切判据,根据各储能单元状态进行优先排序;以频率变化率的死区作为控制策略的切换点,在可变下垂控制的基础上增加SOH变量。通过提出的控制策略来控制储能单元组的投切出力,在保证快速响应电网一次调频的同时也保证了储能电站运行的经济性和安全性。
1 储能电站参与电网一次调频方法
大型储能电站的储能单元组数量较多,常规储能电站拓扑如图1所示。

图1 储能电站并网结构示意Fig. 1 Illustration of energy storage power station into the grid
本文将2种控制策略相结合,虚拟惯性控制一般在负荷扰动初期产生作用,此时频率变化率较大,仅靠下垂控制无法快速降低频率变化率,虚拟惯性控制可快速阻止电网频率恶化且减小最大频率偏差。但考虑储能容量问题,惯性控制不能长时间作用,在阻止频率恶化后,采用下垂控制继续调频,在兼顾储能荷电状态和健康状态的同时减小频率稳态误差。考虑到储能电站的经济性和安全性,基于储能单元SOC、SOH的估算,对各个储能单元组进行运行状态评判,对各储能单元进行合理的投切。含储能系统的电网一次调频模型可以等效为图2所示的动态模型。

图2 储能系统参与电网一次调频的动态模型Fig. 2 Dynamic model of energy storage system participating in primary frequency regulation
其中,s为拉氏算子;KG为传统发电机组的单位调节功率;TG、TCH、TRH分别为传统发电机组的调速器时间常数、汽轮机时间常数、再热器时间常数;FHP为再热器增益; ∆PL(s)为负荷扰动量; ∆PB(s)为储能系统出力;为虚拟惯性控制出力;为虚拟下垂控制出力;M为电网惯性时间常数;D为负荷阻尼系数。
根据以上分析,本文策略在扰动初期频率变化率大时采用引入健康因子的虚拟惯性控制以减缓频率恶化速度及恶化程度;在渡过频率恶化期后采用系数可变的下垂控制并结合SOC、SOH估计对各储能单元组进行优先级排序,响应电网频率波动时,将优先级高的储能单元组投入工作既能保证调频效果又能保证储能电站的经济性和安全性。在调频死区外,当频率偏差∆f>0(∆f<0)时,若频率偏差率 dft/dt>0(dft/dt<0)则启动虚拟惯性控制,所有储能单元同时出力,迅速阻止频率进一步恶化,若频率偏差率dft/dt<0(dft/dt>0)则启动下垂控制,根据各储能单元SOC、SOH对储能变流器(power conversion system,PCS)选择投切,2种控制相互配合最终实现频率的快速恢复。
2 储能电站参与电网一次调频的控制策略
2.1 改进储能系统虚拟惯性控制
为维持电网稳定运行,中国一般规定电网频率偏移为 0.2~0.5 Hz或者–0.5~–0.2 Hz[20],惯性控制在短时内提供大功率支撑电网,可有效缓解频率变化陡度,改进虚拟惯性响应可表示为

式中: ∆Pit为t时刻第i组储能单元的虚拟惯性响应值;Gt为改进虚拟惯性系数; dft/dt为t时刻的频率变化率;Rs为虚拟惯性控制调频死区。虚拟惯性控制在短时间作用,对电池的荷电状态影响较小,因此不考虑SOC变化对其输出功率的影响。
因传统虚拟惯性控制可有效抑制频率扰动初期的恶化程度,但是由于维持虚拟惯性控制需要储能单元输出大功率支撑,循环多次会加速电池老化。本文引入健康因子的概念,结合考虑电池SOH来调整储能系统惯性出力,改进虚拟惯性系数为

式中:G0为固定惯性系数;GH为关于SOH的健康因子;SOH,t为电池t时刻健康状态;SOH,max和SOH,min为电池健康状态上下限,分别为1.0, 0.8。
综上可知,改进的储能电站虚拟惯性控制在电网频率波动初期,通过引入健康因子,所有储能单元根据各自SOH调整出力深度,实现储能电站向电网持续快速地注入有功功率,并有效延缓电池容量衰减速度。
2.2 基于电池状态估计的优先顺序指标
大规模储能电站的储能单元分为若干组,分别经由PCS并联,在实现调频效果的同时也应考虑电池储能的经济安全性,为此,本文在对SOC、SOH估计的情况下,进而对各个储能单元组的动作优先顺序进行分级排序,按照确定的优先顺序选择储能单元组投入工作。
现应用工程一般使用安时积分法进行SOH状态估计,但该方法没有考虑电池多次循环后内部材料的退化、计算损耗等问题,需要频繁进行校准。由此,本文加入一种新的SOC和SOH估计策略,基于电池二阶电路模型,对电池电压的测量值和计算值之间进行实时比较,结合PI控制器,提供更准确的状态估计值。
总体的估算框图如图3所示,其中,V(t)和i(t)为ESS实际运行过程中测得的电压电流。然后将V(t)与电路模型Vmodel(t)提供的值进行比较,并由PI1控制器进行放大,提供一个校正项ΔE0,用于估计空载电压E0。根据厂家提供数据表的关系SOC(E0)来估计SOC,再将其与采用库仑计数法得到的SOC进行比较,经过PI2放大误差,输出∆VRi作为被用作充电和放电期间模型内阻输出的校正因子,在SOC值偏低时, ∆VRi表示内部电阻Ri的增量。
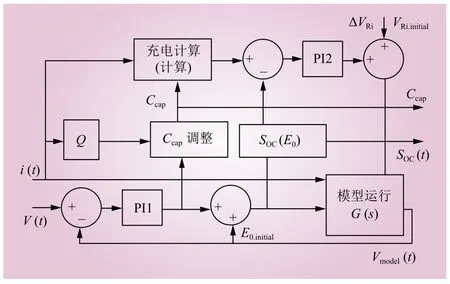
图3 实时SOC和SOH估计策略Fig. 3 Real-time SOC and SOH estimation strategy
SOH的估计方法有多种,本文中SOH计算表示为实际容量Ccap与额定容量Cn的比率。

式中:Q表示为一段时间内电流的时间积分;t=[t1,t2];为开路电压。

可以在不延时的情况下估计Ccap,即

计算得到储能电池关键参数SOC、SOH的值后,为了更好地控制储能单元组的投切,本文引入考虑储能单元SOC及SOH的优先排序工作策略。大规模储能电站在连接方式上选用串并联方式成簇,因此,对储能单元组进行优先排序控制能够最大限度地发挥储能电站的潜力。优先排序的计算式为
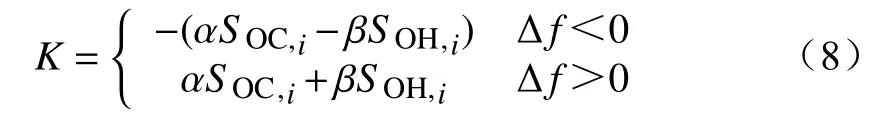
式中:K为优先系数;SOC,i、SOH,i分别为第i组储能单元实时荷电状态、健康状态;α、β为权重系数,α∶β= 1∶2。
根据优先排序计算式得到各储能单元的优先系数,如图4所示,优先系数K越大,储能单元组动作优先级别越高;反之,储能单元组动作优先级别越低。若Δf<0,储能系统吸收电网功率,则优先选择实时SOC较小的储能单元组;若Δf>0,储能系统释放功率支撑电网,则优先选择实时SOC较大的储能单元组,充放电2种情况均优先考虑SOH更好的储能单元。

图4 储能单元优先排序示意Fig. 4 Schematic diagram of energy storage unit prioritization
为方便下垂系数的修订,依据储能单元SOC将其荷电状态进行划分,SOC,max、SOC,max-s、SOC,min-s、SOC,min分别为储能单元组的正常工作上限、稳定工作上限、稳定工作下限和正常工作下限。
2.3 基于SOC、SOH的储能系统可变下垂控制
储能电站辅助调频的下垂控制是在下垂特性的基础上根据频率偏差控制储能系统的有功输出,从而稳定电网频率。传统频率下垂控制策略为

在传统下垂控制的基础上加入SOC、SOH2个变量实现下垂系数可变,并且结合对多组PCS的优先投切控制,实现对电网频率偏差控制以及使储能单元维持在健康状态。
充放电工况不同SOC、SOH值对下垂系数影响为

(1)电池充电工况。
当SOC∈[0,SOC,min]时,储能电池电量充足,故不考虑荷电状态系数以最大化保证调频效果,计算式为

(2)电池放电工况。

所提改进下垂控制策略根据不同SOC、SOH实时计算下垂控制系数来控制储能单元输出功率大小。当电网频率波动时,储能单元根据自身状态动态调节出力大小,在保证电网频率需求的同时尽可能使储能电池处于健康安全的状态。
3 储能电站参与一次调频的综合控制策略
3.1 调频综合控制策略
在上文讨论的控制策略中,各控制的动作时机和动作效果都不相同,为优化储能电站的调频效果及保持储能单元状态,提出的优化控制策略如图5所示。以 ∆f>0,即储能系统需要释放功率支撑电网为例。
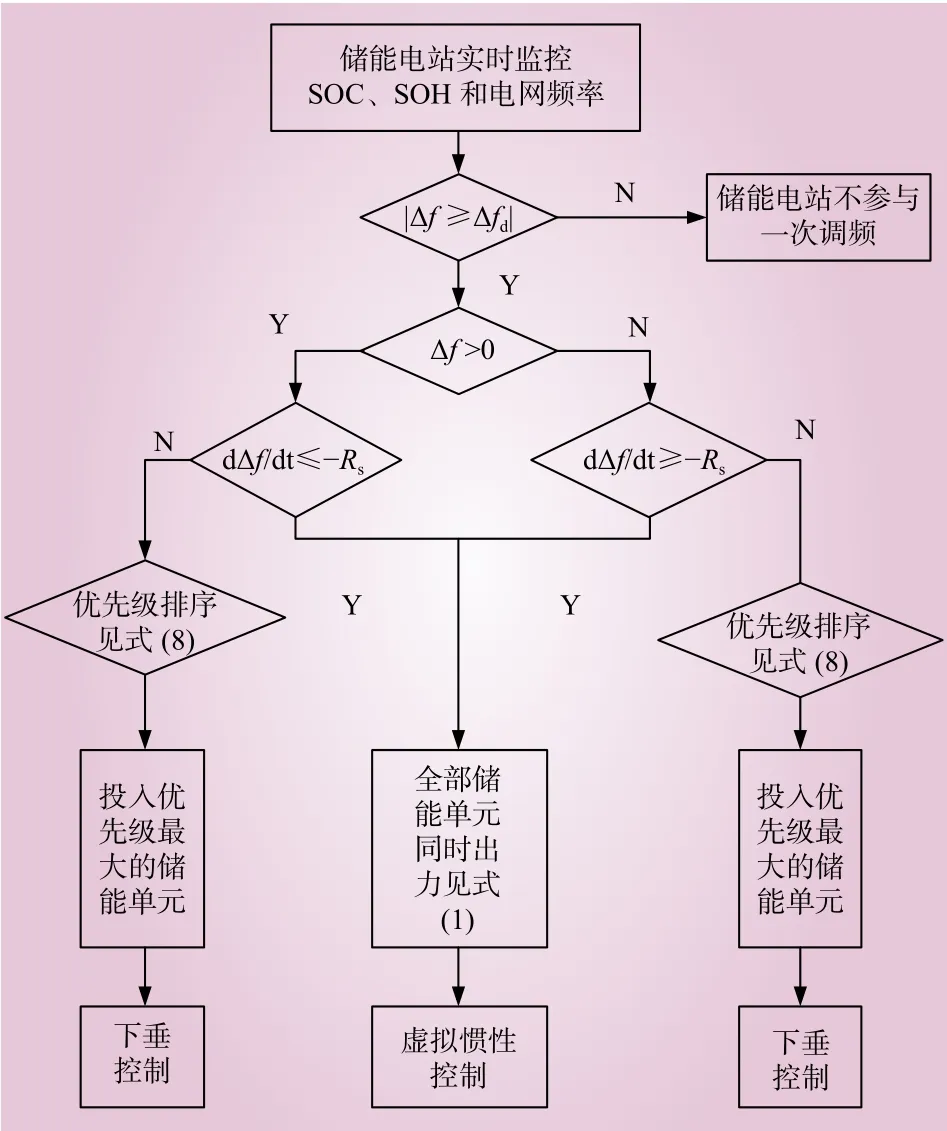
图5 储能电站参与一次调频的综合控制策略Fig. 5 Integrated control strategy for primary frequency regulation of energy storage power station
(1)储能系统实时监测电网频率ft以及各储能单元的SOC、SOH,参考国内关于调频偏差死区的标准,调频死区fd=0.033 Hz。当实时电网频率与参考电网频率差值大于fd时,进入下一步判断,否则循环监视。
(2)当 ∆f>0且频率变化率为负 (dft/dt<0),若频率变化率的绝对值超过了虚拟惯性控制死区Rs,此时虚拟惯性控制启动,所有储能单元按照式(1)计算出力,同时响应电网一次调频。
(3)当频率偏差达到最大,即 (dft/dt=0),此时进入频率恢复阶段时,虚拟惯性控制闭锁。
(4)启动下垂控制之前,根据监测得到的SOC、SOH值以及式(8)对各储能单元进行优先级排序,将优先系数大的储能单元投入运行,优先系数大则代表该储能单元的SOC及SOH在所有储能单元中均处于良好状态。在此基础之上投入运行的储能单元采用系数可变的下垂控制进行有功功率输出以恢复电网频率。
储能电站充电 (∆f<0)时的控制策略和上述过程类似。
3.2 调频评价
为了评价储能系统运用本文策略参与电网一次调频的效果,在分析幅频特性的基础上得出时域评价指标。
在阶跃负荷扰动的工况下,提出4个关键评价指标, ∆fs为扰动后的稳态频率偏差,代表调频的最终效果, ∆fm为最大频率偏差,代表对扰动的抑制效果;ts为调频完成时间,代表储能系统整体响应速度,tm为调频峰值时间,代表储能惯性响应的支撑速度,其值均越小越好。
在连续负荷扰动的工况下,主要将频率偏差和荷电状态偏差的均方根值作为一次调频的评价指标,以此来反映一次调频效果和储能单元的电量健康。

式中:ft为t时刻电网实时频率;QSOCt为t时刻储能单元实时荷电量;f0为参考频率,设为50 Hz;QSOC_ref为参考荷电量,设为0.5;f、Q分别代表频率指标和荷电状态指标。
4 仿真验证
本文所提控制策略以搭建区域模型为基础,模拟储能电站结构加入多组储能单元进行仿真验证。
系统额定频率为50 Hz,包括1台额定容量为100 MW的传统火电机组,3组储能单元并联组成额定容量为 3.15 MW/6.33 (MW·h)的储能系统,其额定电压为380 V,系统仿真示意如图6所示,参数标幺值是以额定频率50 Hz和传统机组额定容量作为基准值。为了说明本方法的适用性,以2种不同工况进行分析说明。

图6 系统仿真示意Fig. 6 System diagram for simulation
4.1 阶跃负荷扰动工况
假设在阶跃负荷扰动中A、B、C 3组储能单元的初始SOC分别为0.9、0.85、0.75,当电网正常运行时,加入幅值为0.015标幺值的阶跃扰动,对比在本文控制策略、定K系数控制法和无储能3种不同策略下电网频率恢复情况以及各储能单元荷电状态变化情况,结果如图7所示。

图7 阶跃扰动下系统响应仿真结果Fig. 7 Simulation results of system response under step disturbance
由图7 a)可知,因惯性控制作用,本文方法相较其他2组方法对于扰动初期的频率恶化程度抑制效果明显,无储能下降斜率最大,其次是定K法。相较于无储能来说定K法的频率最大偏差较小,由于定K法全程采用固定功率对电网进行调频,其储能系统因电量快速被耗尽而过早停止运行。本文提出的控制策略在频率偏差及频率偏差率超过惯性控制和下垂控制的调频死区时,2种控制策略分别作用,使得系统的最大频率偏差、频率下降斜率均最小。为延长电池使用寿命以及考虑储能电站安全性、经济性,采用下垂法控制电池放电时,考虑3组储能单元的剩余电量,优先将处于充电饱和区域的A组储能单元投入系统运行,其余单元组暂时停止工作。
由图7 b)可知,在频率变化初期虚拟惯性控制3组储能单元同时投入运行;频率偏差达到最大值时,虚拟惯性控制闭锁启动下垂控制,考虑运行工况及各储能单元状态,经式(8)计算,A组储能单元优先级最高投入运行,B、C 2组暂停工作,经过1个周期重新判定,C组仍不参与调频,A组切除,B组储能单元投入运行,如此往复,最终达到1次调频效果。3组储能单元SOC以均衡的趋势下降且均处于健康工作区内。本文综合策略相较其他方法有明显优势,在大规模储能应用中,能更好地发挥储能潜力,保持电池容量。
调频评价指标如表1所示,由表1可以看出,在阶跃负荷扰动工况下,本文方法有效减小了最大频率偏差和最终的稳态误差,且到达稳态误差的时间更短。
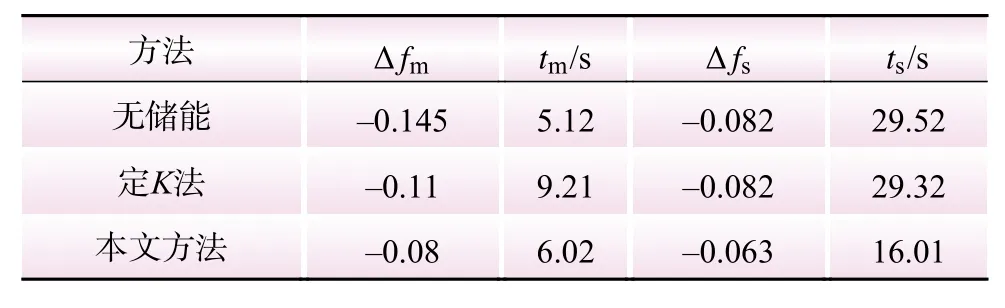
表1 阶跃负荷扰动评价指标Table 1 Evaluation index of step load disturbance
4.2 连续负荷扰动工况
储能参与电网调频作用时间较短,为了使仿真结果更加明显,体现本文控制策略的作用效果,故将A组储能单元初始SOC设为临界充电状态0.9,B组SOC设为0.6,C组SOC设为临界放电状态0.2。因为储能辅助电网一次调频主要是应对较小幅度的负荷扰动,通常约为负荷峰值的1%,因此,本文假设连续负荷的变动平均幅值为1%~3%。
连续负荷扰动曲线如图8a)所示。不同控制策略下电网频率偏差曲线如图8b)所示,本文所提控制方法下3组储能单元SOC变化曲线如图8c)所示,评价指标如表2所示。

图8 连续扰动下系统响应仿真结果Fig. 8 Simulation results of system response under continuous disturbance

表2 连续负荷扰动评价指标Table 2 Evaluation index of continuous load disturbance
由图8 b)可知,在连续负荷扰动下,本文所提控制策略对比无储能和采用下垂定K法,频率偏差的情况明显降低,更好的保障电网安全稳定运行。由图8 c)可知,由于A组储能单元处于临界放电状态,相较于B组放电功率更大,SOC下降更快,C组处于临界充电状态,在系统功率缺额时不参与工作,仅在系统功率过剩时投入工作,避免电池出现过放情况,最终各储能单元组的荷电状态均向健康的工作状态变化。对比其他单一储能单元的控制方法,本文方法考虑实际工况,更适用于工程应用,避免电池过充过放情况发生的同时也达到了较好的调频效果,验证了本文控制策略的有效性。
由表2中数据可以看出,连续负荷扰动工况下无储能调频效果最弱,本文策略略优于定K法,并且对于Q指标,本文所提方法考虑电池状态对出力深度的影响,仿真结果显示较好。由于大量新能源发电并网,电网频率扰动的次数更加频繁,储能调频更应在安全的前提下利用好本身能量转换的优势。
5 结论
运用本文所提控制策略,在电网需要时提供必要的功率输出,目前所提调频策略中,并未考虑其结构中电池簇并联运行的实际情况。在调频效果相当的情况下,把延长电池使用寿命作为切入点进行研究就显得尤为重要,本文研究重点也在于此。通过仿真也验证了其有效性。
(1)本文提出的综合控制策略考虑了储能电站内部储能单元的并联运行结构,在估计各个储能单元SOC、SOH的基础上,对多组储能单元进行投切控制,在保证对电网调频效果的同时,使电池尽量处于安全工作区域中。
(2)所提方法的适用性较好,无论是在阶跃扰动还是连续扰动下,都能使电网频率快速的回归到稳态偏差,保证了电网频率的稳定性。
(3)在频率变化初期,为了防止频率进一步恶化,所有储能单元同时参与虚拟惯性控制共同出力,频率偏差变化率下降至惯性控制死区外后,根据各储能单元状态进行优先级排序,启动下垂控制,配合各储能单元进行调频。充分发挥储能电站多储能单元并列运行的优势。
