抛物型Baouendi-Grushin Laplace方程解的估计 ①
2022-03-02元琛黄小涛
元琛, 黄小涛
南京航空航天大学 理学院,南京 211106
令x∈Rn,y∈Rm,γ>0, Baouemdi-Grushin(B-G)向量场[1]为
B-G梯度可定义为
对应的B-G型拉普拉斯算子为
Δγu=(γ·γ)u=Δxu+|x|2γΔyu
其中Δx,Δy分别是Rn和Rm空间上的拉普拉斯算子.
当γ=1时, 文献[2]研究了方程
Δ1u1=Δxu1+|x|2Δyu1=g1(x,y)
(1)
此方程与Cauchy-Riemann Yamabe问题有密切关系.
当γ是正整数时, 向量场Xi和Xj满足Hörmander条件[3]. 由此得到方程的Hε正则性估计.
若γ为任意的正数时, 向量场Xi和Xj仅为Hölder连续, 不满足Hörmander条件, 所以不能得到Hε正则性. 文献[4-6]通过研究与B-G向量场相关的加权Sobolev-Poincare不等式, 证明了Harnack不等式和方程解的Cα估计.
(u2)xx+x(u2)yy=g2(x,y),x∈R1,y∈R1
(2)
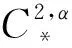
退化抛物B-G方程也引起了众多学者的关注[3,14]. 随后, 文献[15]研究了抛物p-Laplace类型的B-G方程并证明了一些存在性结论. 文献[16]研究了带有初值问题的分数阶p-Laplace B-G方程, 通过引入与B-G向量场相关的内在度量, 用紧方法证明了方程解的Lq正则性估计.
对于抛物型B-G方程, 假设Ω⊂Rn×Rm是一个有界开区域, 抛物区域为Ω*=Ω×(0,T], 则抛物边界为∂Ω*=(∂Ω×(0,T])∪(Ω×{t=0}). 我们将研究下述抛物B-G拉普拉斯方程
(3)
其中f=(l1, …,ln,ln+1, …,ln+m).
本文主要证明的结论如下:

在区域{(x,y,t)∈Ω*:x=0}附近, 此方程为退化抛物方程; 如果远离{x=0}区域, 则方程没有退化性. 我们将分别研究在{x=0}附近区域和远离{x=0}的区域的解的正则性, 并给出方程解的一致性估计.
1 预备知识
本节我们给出弱解的定义和一些重要的引理.
1.1 内在度量
首先为了能对B-G向量场进行分析, 我们引入C-C度量.
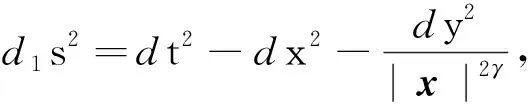
当|x|, |y|~1时, 抛物C-C距离可看成经典的抛物距离
令Z=(x,y,t),rZ=(rx,r1+γy,r2t), 在抛物C-C度量下, 算子L满足性质
L(u(rx,r1+γy,r2t))=r2(Lu)(rx,r1+γy,r2t)
(4)
本文记
Qr(Z0)={(x,y,t): (x,y)∈Sr(z0), -r2 为方便书写, 记Sr=Sr(0),Qr=Qr(0). 另外对x∈Rn,y∈Rm,z∈Rn×Rm, 记dx=dx1dx2…dxn, dy=dy1dy2…dym, dz=dx1dx2…dxndy1dy2…dym. 其范数定义为 (5) 且在有界区域上此嵌入为紧嵌入. 方程(3)的弱解可定义如下: (6) 那么称u是方程(3)的弱解. 定义局部可积函数v∈L1(Ω*)的极大值函数为 对于极大值函数, 有以下结论: (2)如果v∈Lp(Ω*), 其中1 以及 文献[19]证明了Lp函数的一个测度估计. 引理2[19]若函数u是区域Ω*中的一个可测函数, 常数θ>0,λ>1, 2≤p<∞, 则 且有估计 为了研究解的梯度估计, 我们还需引入改进的Vitali覆盖引理. 引理3[20]设0<ε<1,A⊂B⊂Q1是Q1中的两个可测集, 满足|A|<ε|Q1|. 如果对任意的z∈A,r<1, 只要|A∩Qr(z)|≥ε|Qr(z)|, 都有Qr(z)∩Q1⊂B. 那么存在常数C, 使得 |A|≤Cε|B| 本小节我们研究在区域{(x,y,t)∈Q1:x=0}附近的正则性. 由C-C度量可知, 不妨假设u满足方程 ut-Δγu=divγf(x,y,t) 则v(x,y,t)=u(rx,r1+γy,r2t)在{x=0}附近满足方程 vt-Δγv=r2divγf(rx,r1+γy,r2t) 首先给出在Q1内的能量不等式. 引理4设u是方程(3)的弱解, 那么有 (7) 那么 对时间t积分, 整理可得 定理2设u是方程(3)的弱解. 若对任意的ε1>0, 都存在一个δ(ε1)>0, 满足条件 则存在函数h使得 ht-Δγh=0,Z∈Q1 (8) 且有 (9) 且有 (10) 但是 (11) 令n→∞, 由(9)式和(10)式可得 这说明了u∞和h都是方程(8)的弱解. 这与(11)式矛盾, 证毕. 定理3对任意的ε>0, 存在一个δ(ε), 如果 ut-Δγu=divγf,Z∈Q2 且有 则存在一个函数h满足 ht-Δγh=0,Z∈Q2 使得 证取φ=η2(u-h)并带入(6)式, 那么有 以及 同样的由τ-Cauchy不等式可得 对任意的τ>0, 取τ足够小使得0<τ<δ2, 上式两端对时间t积分, 又由于 则有结论 Q1∩{M(|γu|2)≤1}∩{M(|f|2)≤δ2}≠Ø (12) 那么 (13) 证由(12)式, 假设存在一个点Z0∈Q1, 使得对任意的0 由于Q2⊂Q4(Z0), 所以 (14) 由定理3可知, 对任意的ε=η>0, 存在一个δ(η)和弱解h满足 ht-Δγh=0,Z∈Q2 以及 那么 (15) 引理4表明存在一个常数N0, 使得 当r≤2, 有 当r>2时, 注意到Qr(Z1)⊂Q2r(Z0), 有 进一步可得 (16) 综上可知 取δ=δ(η)充分小, 可以得到 定理4给出了方程(3)解在(0,0,t)点附近的正则性估计. 同样可以得到在区域Y=(0,y,t)附近解的估计. 推论1设u是方程(3)在Qr(Y)内的弱解. 存在一个常数N1>0, 对任意的ε>0, 存在一个δ>0, 如果 Qr(Y)∩{M(|γu|2)≤1}∩{M(|f|2)≤δ2}≠Ø 那么 2.1节得到了在{(x,y,t)∈Q1:x=0}附近的估计. 接下来研究在Q1⊂Ω*内的任意一点的估计. (17) 则有 Qr(Z0)⊂{Z∈Q1: M(|γu|2)>1}∩{Z∈Q1: M(|f|2)>δ2} 证当d(Qr(Z0), {x=0})≤10r时, 可以通过反证法证明. 假设结论不对, 即 Qr(Z0)∩{Z∈Q2: M(|γu|2)≤1}∩{Z∈Q2: M(|f|2)>δ2}≠Ø 令Y0=(0,y0,t0), 那么Qr(Z0)⊂Q13r(Y0)⊂Q30r(Z0), 也就是 Q13r(Y0)∩{Z∈Q2: M(|γu|2)≤1}∩{Z∈Q2: M(|f|2)>δ2}≠Ø 根据推论1, 对任意的ε>0, 有 其中Cγ=30-n-m(γ+1). 由此可得 与(17)式矛盾, 这就证明了第一种情况. 当d(Qr(Z0), {x=0})>10r时, 不妨假设x0≠0. 记 (18) 前文已经指出, 若|x|,|y|~1, 那么 d1s2~ds2=dt2-dx2-dy2 (19) 根据二阶抛物方程经典的Lp理论[22]可知存在常数N0和δ>0, 对任意的ε>0, 如果 那么 其中h(x,y,t)满足方程 最后变换回来得u(x,y,t)在球Qr(Z0)内的估计, 即如果 {M(|f|2)≤δ2}∩{M(|γu|2)≤1}∩Qr(Z0)≠Ø 那么 引理6设u是方程(3)在Q1内的弱解. 如果 则存在ε1=C(γ)ε, 使 证记 由Vitali覆盖引理3, 再根据推论1、 引理5有 进一步用有限数量的Qri(zi)去覆盖Q1即可得结论. 推论2设u是方程(3)的弱解. 存在ε1=C(γ)ε, 使 证下面用归纳法证明. 当k=1时, 由引理6知结论显然成立. 根据归纳假设, 故对k+1的情况也成立, 易知结论成立. 定理1的证明当p=2时, 由能量不等式可得结论. 令p>2, 根据假设 由条件可知存在一个常数N1, 使得对任意的ε>0, 有一个δ>0, 对任意的r∈(0, 1), Qr∩{M(|γu|2)≤1}∩{M(|f|2)≤δ2}≠Ø 由引理6知 再根据推论2得到 从引理1知, 存在一个常数C使得 也即 于是有 γu∈Lp(Q1) 且满足 ‖γu‖Lp(Q1)≤C(‖f‖Lp(Q2)+‖u‖Lp(Q2)) 综上所述, 结论得证.1.2 Sobolev空间
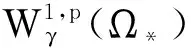
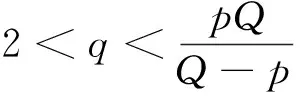

1.3 引理

2 正则性估计
2.1 {(x, y, t)∈Q1: x=0}区域附近的估计

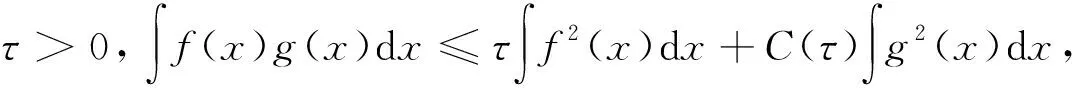
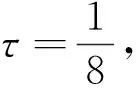

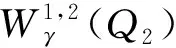
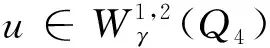
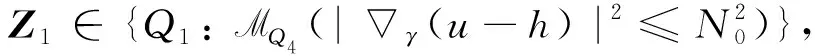

2.2 远离{(x, y, t)∈Q1: x=0}区域估计

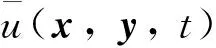
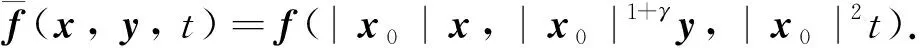
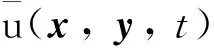
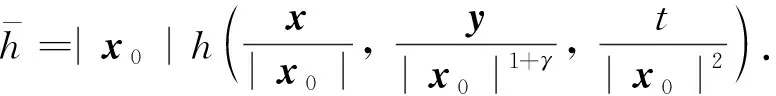
2.3 主要定理的证明



