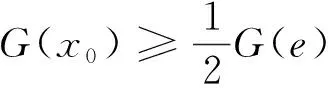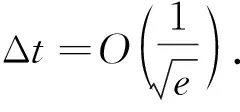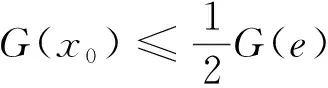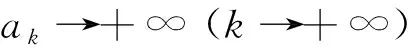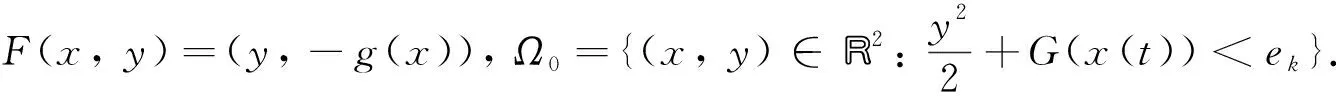二阶共振哈密顿方程重周期解 ①

邢秀梅

伊犁师范大学 应用数学研究所， 新疆 伊宁 835000

平面时变Hamilton周期系统的一个典型模型是x″+f(t，x)=0， 其中f(t，x)∈C1(R×R， R)关于变量t是2π周期的． 关于此系统周期解的存在性和重性的研究已开展了很多工作： 关于半线性非奇异位势的工作见文献[1-7]， 关于奇异位势的工作见文献[8-11]， 关于扰动方程的工作见文献[12-14]． 本文考虑二阶半线性共振Hamilton方程：

x″+g(x)=p(t，x，x′)

(1)

(2)

p满足

(3)

有界、 连续且关于第一个变量是2π周期的．

当p(t，x，y)=p(t)时， 方程(1)即为Duffing方程：

x″+g(x)=p(t)

(4)

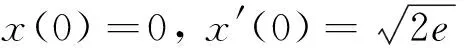
(5)

和全局李普希兹条件

|g(x)-g(y)|≤L|x-y|(其中L为常数)

(6)

下， 证明方程(4)至少存在一个2π周期解和无穷多次调和解． 文献[3]将文献[1]中的振动位势条件减弱为弱振动位势

(7)

亦得到类似结论． 文献[4]去掉李普希兹条件， 增加弱振动位势条件和共振条件

(8)

得出方程(4)至少存在一个2π周期解．

最近在条件

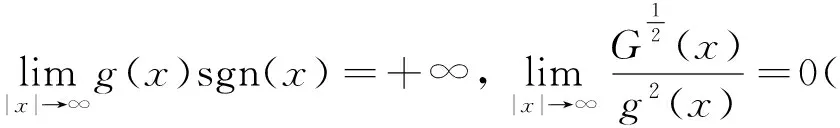
(9)

与条件

(10)

下， 文献[5]证明方程(1)至少存在一个2π周期解． 注意条件(10)排除了τ(e)的共振点． 一个自然的问题是： 在半线性共振条件下， 加怎样的条件能保证方程(1)存在周期解． 本文结论如下．

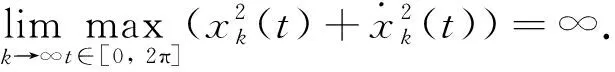
为了证明定理1， 先给出一些引理．

引理1[4]设条件(2)成立， 则存在常数e0>0， 使得当e>e0时，Γe是一条包围原点的星形闭曲线．

引理2[4]设条件(2)成立，M为固定常数， 对满足0≤y-M≤u≤y≤e的u和y， 有

考虑方程(1)的等价系统

x′=yy′=-g(x)+p(t，x，y)

(11)

它的极坐标形式为：

(12)

以(r(t)，θ(t))， 表示方程(12)满足(r(0，r0，θ0)，θ(0，r0，θ0))=(r0，θ0)的解． 类似文献[4]可得：

引理4假设条件(2)成立， 则有：

1) 方程(11)(或(12))的每个解都在t轴上存在；

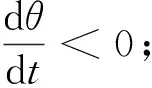
引理4结论2)表明， 在任意确定的时段内， 对充分大的e， 自Fe上出发的方程(11)的解Λ是绕原点顺时针旋转的． 记解Λ绕一圈所用的时间为T．

证参考文献[4]方法． 证明过程分两步．

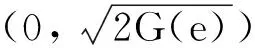
(13)

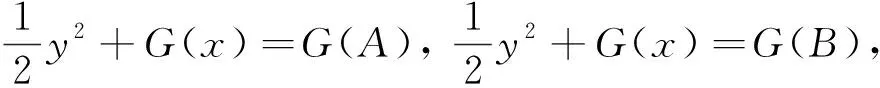
当t∈[α，t1]时， 有A≤x≤x(t1)． 由于x′(t1)=0， 方程(11)得

设δ(A)=inf{g(x)：x≥A}， 由条件(2)， 当A≫1时， 存在c>0， 使得δ(A)>cA， 因此

(14)

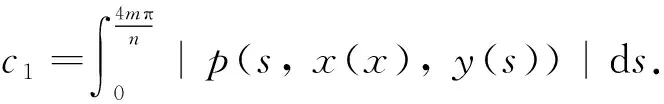
由条件(2)和式(13)知， 存在常数M>0使得B-A

(15)

两边积分得

由引理 3、 条件(2)和式(13)， 综合可得

(16)

进而

对解Λ经过第i象限的时间ti(i=2，3，4)有类似估计， 最后可得

2) 对一般的从(x0，y0)∈Fe出发的解Λ， 只需再估计解Λ通过下述区域

所需时间Δt．

x-

(17)

(18)

对任何正整数j， 设Tj(e)是从Fe上出发的解转j圈所用的时间， 由c1e0和c1<τ(e)

(19)

1) 当(r0，θ0)∈Fak时，θ(2mπ，r0，θ0)-θ0<-2nπ；

2) 当(r0，θ0)∈Fbk时，θ(2mπ，r0，θ0)-θ0>-2nπ．

θ(2mπ，r0，θ0)-θ0<-2nπ

如果j=n， 那么对k足够大， 有

从而

因此

可类似证明结论2)．

再证明2π周期解的存在性． 考虑

x″+g(x)=λp(t，x，y)λ∈[0， 1]

(20)

定义如下算子

这说明解F在2mπ时间内围绕原点顺时针运动超过n圈， 但是达不到n+1圈， 所以不是2mπ周期解， 也不是2π周期解．