改进的IPMSM单张表转矩转速二维查表法

冯 雷，张志锋

(沈阳工业大学 电气工程学院，沈阳 110870)

0 引 言

内置式永磁同步电机(以下简称IPMSM)结构简单、加工简易、体积略小、质量轻、损耗小的同时效率能达到更高，相较传统电机，成为电动汽车电驱动系统中认可度十分高的选择。而使用永磁体励磁的IPMSM无法像常规电机一样可以通过改变励磁绕组而达到调节励磁磁场，永磁体产生的磁场是无法改变的，只能通过削弱d轴电流来等效达到削弱磁场的目的。

负id补偿控制算法由于其不包含电机参数的公式且参数鲁棒性较强，成为弱磁控制研究热点。但其控制算法本身的问题，只能通过削弱d轴电流来进行弱磁升速，弱磁深度受到限制。当电机在深度弱磁区域时，随着弱磁深度的加深，电压椭圆与电流圆会出现不重合的现象，此时逆变器端电压过大，会带来严重后果[1]。同济大学康劲松教授团队通过使用单电流调节器方法替换传统控制方法实现弱磁控制，通过减少控制变量数目，一定程度上解决了交直轴电流的耦合问题，并通过计算转折速度处电流点找到MTPA(最大转矩电流比)与弱磁控制的切换点，实现了两种控制比较平滑的过渡[2-3]。湖南大学罗德荣团队通过找到进入MTPV(最大转矩电压比)曲线的iq电流点，与特征电流点进行线性化处理，线性化MTPV曲线，但在不同电机中进入MTPV曲线的iq电流点难以获取，计算上依旧十分复杂[4]。大连交通大学时维国团队针对深度弱磁区域电流、转矩脉动大，电流调节器易饱和等问题，计算深度弱磁MTPV曲线id、iq关系，通过将id下限限制在特征电流点，以此推导出Δid与Δiq的比例式。对d轴电流进行限幅，确定q轴电流增量，重新规划弱磁轨迹，达到深度弱磁的目的，但此比例式参数十分复杂，在实际中难以应用[5]。江苏大学朱利东团队优化了Δid与Δiq的比例关系，其计算量小，易于实现，并在实验中得到了验证[6]。

查表法基于电机实测标定，无需额外的控制过程。本文基于查表法介绍一种单张表转速转矩二维表查表法，具有动态性能好，无额外计算过程优点的同时，为了应对电机运行过程中母线电压的波动，与多张表查表法标定不同，通过推导公式将母线的电压波动转换为转速波动，在母线电压波动情况下也可以在单张表中进行查询，省略了多张表多个电压下标定的复杂工程量，最后通过MATLAB/Simulink搭建仿真模型进行验证。

1 IPMSM弱磁机理

本文给出IPMSM在dq轴坐标系下定子电压方程和定子磁链方程[7-8]：

(1)

(2)

式中：ud，uq为d，q轴定子电压；ψd，ψq为d，q轴定子磁链；id，iq为d，q轴定子电流；p为微分算子；R为定子电阻。

式(1)中，永磁电机定子部分电阻较小，当电机运行在弱磁区域转速较高时，电阻上的压降可以忽略不计；当电机处于稳态运行时，第二项微分项也可忽略不计。此时 IPMSM的高速稳态电压方程可以表示如下:

(3)

电机交直轴电压和电流以及逆变器直流侧电压都有一定限制[9]，如下：

(4)

(5)

将式(3)代入式(5)后，电压限制可以用id与iq进行表示，即极限电压椭圆表示如下：

(6)

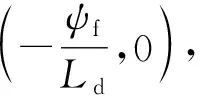
图1 IPMSM 电气约束与运行区域

2 最大转矩电流比曲线

与表贴式电机未达到转折速度即未进入弱磁区域的id=0控制方法不同，IPMSM存在Ld、Lq不同的情况，永磁同步电机电磁转矩方程如下：

(7)

(8)

(9)

式中：Te为输出电磁转矩；Tm为磁阻转矩；Tr为永磁转矩；p为极对数。表贴式电机Ld=Lq，磁阻转矩为0，永磁转矩与iq无关，为了提高效率，采用id=0控制方法。而IPMSM中Ld与Lq并不相同，使用id=0控制方法会降低效率。为此，我们通过拉格朗日定理求极值，可以得出单位电流上获得最大转矩的id分布如下[10]：

(10)

考虑到实际电机运行过程由于发热等问题，Ld、Lq会有微小的变化，通过对如表1所示的电机仿真参数，在MATLAB中进行薄板样条插值，得出随着id、iq变化而改变的Ld、Lq数据，如表2所示。

通过对表2数据进行薄板样条插值，得到如图2所示的三维曲面。

表2 仿真Ld/Lq参数

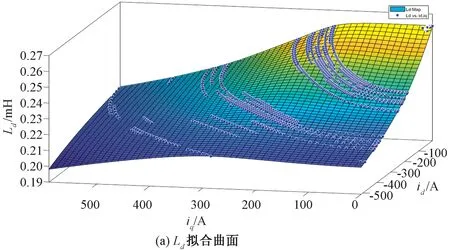
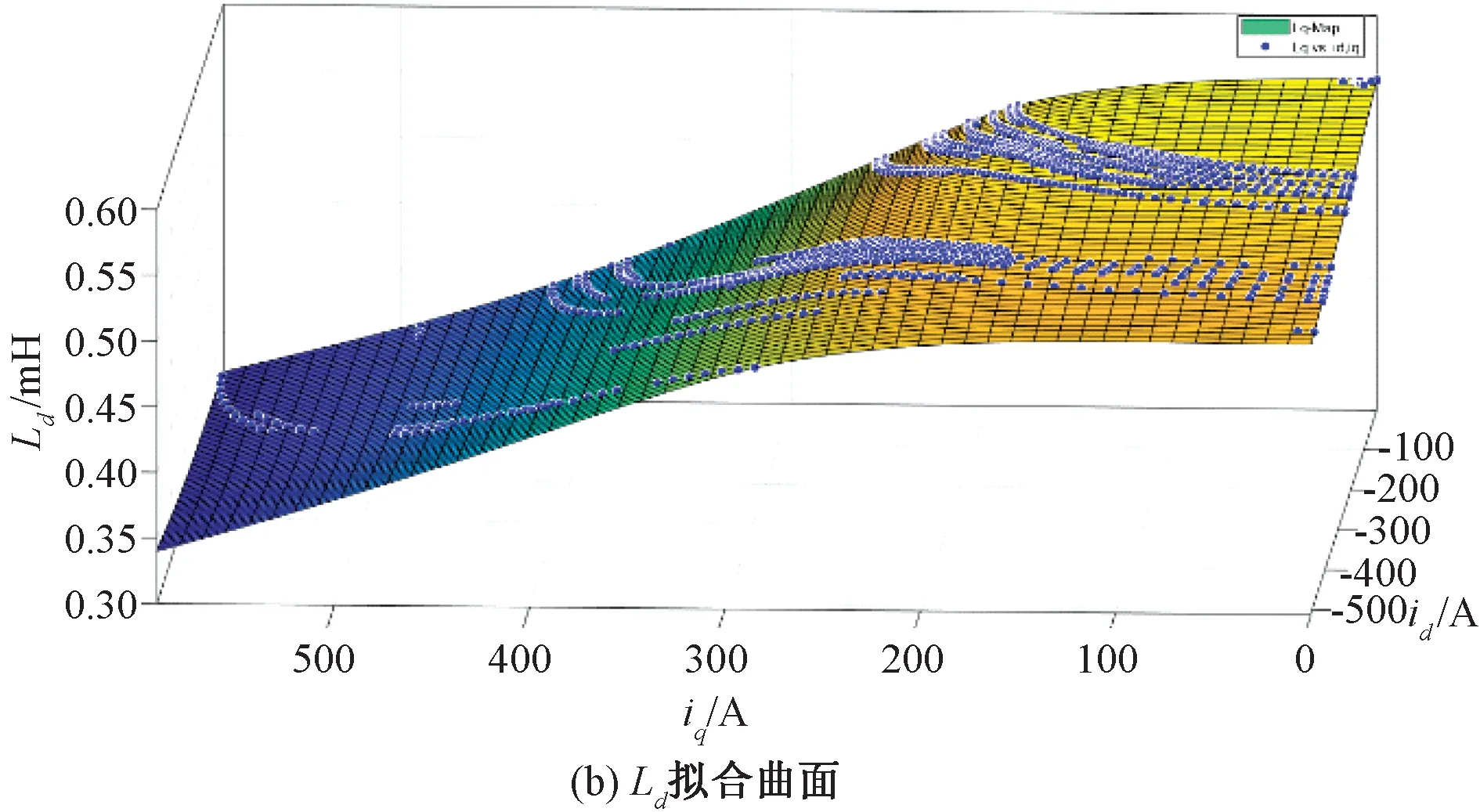
图2 三维曲面

将定子电流is，转矩角β，d、q轴等效电感Ld、Lq代入转矩公式，通过扫描法可以得出MTPA曲线：

(11)

通过两个循环，扫描is从0以每次增长1A的步长到ismax，以及转矩角从90°以每次0.5°的步长到180°，代入式(11)，得到所有转矩情况，调用max函数，获得一组Temax,记录此时的角度β，并通过式(12)：

(12)

得到此时的id、iq并记录，MTPA曲线如图3所示。

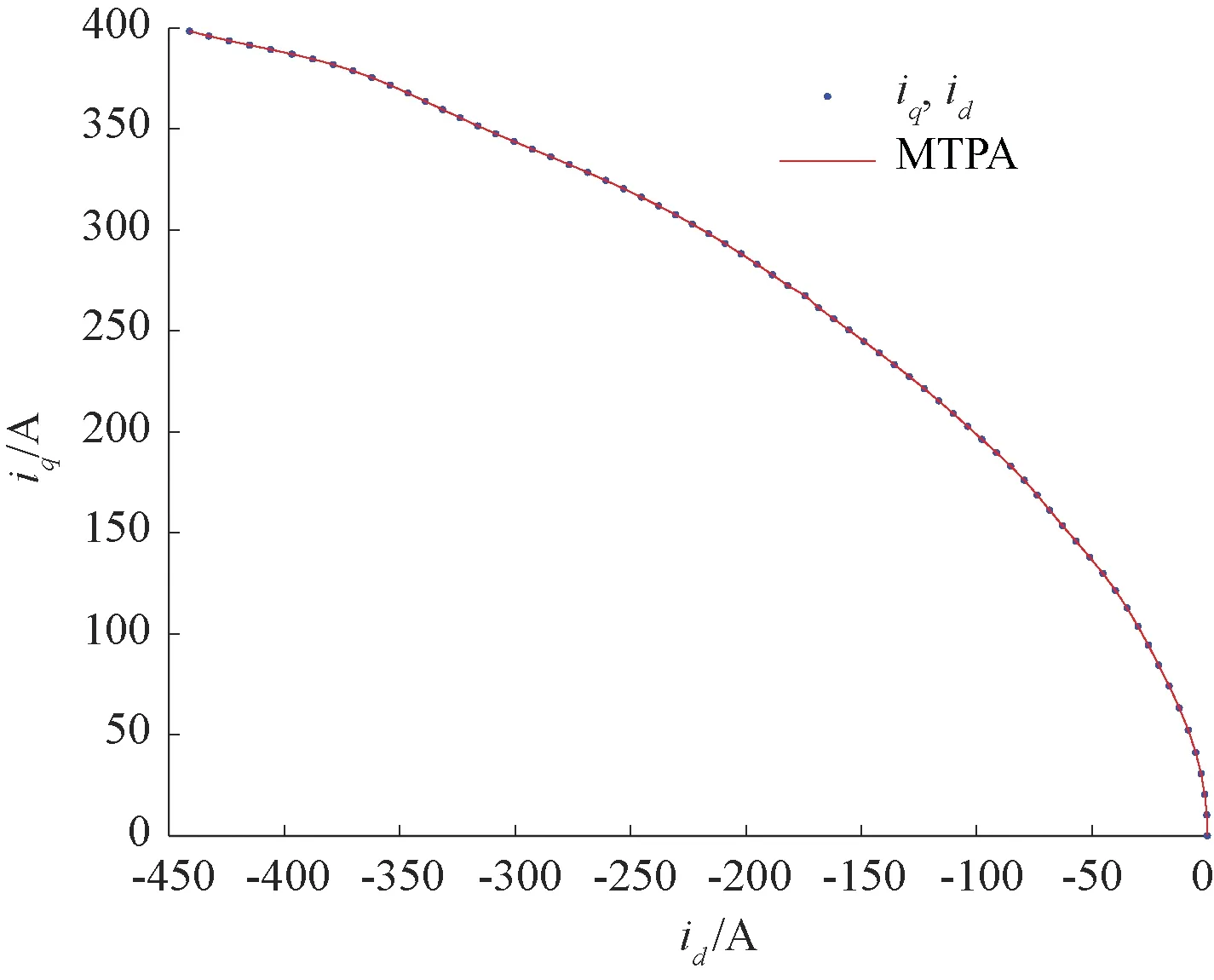
图3 MTPA曲线

3 转矩转速曲线簇

为了获得从MTPA切换到弱磁控制的转折点即转折速度，需要在限制电压椭圆和限制电流圆绘制转矩转速等高线，获得转矩等高线与MTPA的交点对应的转速。扫描转矩从0开始，以10 N·m步长增长到690 N·m，借用MATLAB脚本文件获取等高线，并在此基础上将MTPA曲线加入显示，如图4所示。

图4 转矩等高线

转速在每个转矩下都从0开始，以100 r/min步长增长到5 500 r/min，将上述曲线簇与MTPA曲线放在同一图中显示，如图5所示。

图5 转矩转速等高线簇

记录在各个转矩等高线与MTPA曲线的交点向量值Nem即转折速度以及此时的id _MTPA、iq_MTPA为后续从MTPA切换到弱磁点做基础。

4 最大转矩电压比

最大转矩电压比，顾名思义就是在电压极限椭圆内任一范围获得能获得的最大转矩，构造一个自变量x为id因变量z为Tmax以及中间变量y为iq的函数f并调用fminbnd极小值函数，求出按照定步长增长的每一转速下的最高转矩Tmax以及此时的id _MTPV、iq _MTPV，将这个最高转矩记录下来，为后续MTPV转折做准备。即：

f函数如下：

最后调用fminbnd极小值函数，最高转矩Tmax时对应的id _MTPV、iq _MTPV：

(id _MTPV,Tmax)=fminbnd[Tmax,minN_id(n),

maxN_id(n)]

iq _MTPV=转速曲线簇{n}(id _MTPV)

此时已经完整获得每一个转速下在MTPV曲线转折的最高转矩Tmax，以及MTPA曲线转折速度向量点Nem。除了MTPA和MTPV以外，剩下的电流规划为转矩转速等高线的交点，通过同样的方法通过构造一个自变量为id将自变量代入转矩转速等高曲线簇拟合曲线作差，调用fminbnd函数取极小值，目的是为了获取转矩转速等高线交点时的id、iq。

按照如图6所示的流程图进行表格的建立。

图6 表格建立流程图

按照图6最后得出在udc=270 V全速域MTPA、弱磁、深度弱磁MTPV中id、iq分布。

5 应对电压波动改进单张表

由于存在电压波动情况，当电压波动时本文讨论的udc=270 V便不再适用，因此需要在不同母线电压情况下生成不同的表，工作量十分巨大，对此我们进行如下推导。

高速时忽略电机定子电阻的影响，可有下面的极限电压椭圆方程：

(13)

为了能适应全范围电压运行，先在最低母线电压udcmin下生成id、iq地图，对于上面的电压极限圆来说,可以有如下方程:

(14)

由于二维表查表法的输入是转速和转矩，对于固定的udc得到上述的二维表id、iq地图，但无法应对电压的变化，可以将电压的变化折算到转速的变化上，对于变化的udc,我们可以得到：

(15)

化简可得：

(16)

通过上述变化，可以将电压的变化比例折算到两个输入之一的转速上，这样就可以避免为了应对电压波动重复建立多个表的复杂过程，采用单个表即可。

6 仿真实验

仿真实验在MATLAB/Simulink 2018a编译环境下运行，电机数据见表1。参考转速与母线电压如图7、图8所示。

图7 参考转速设定

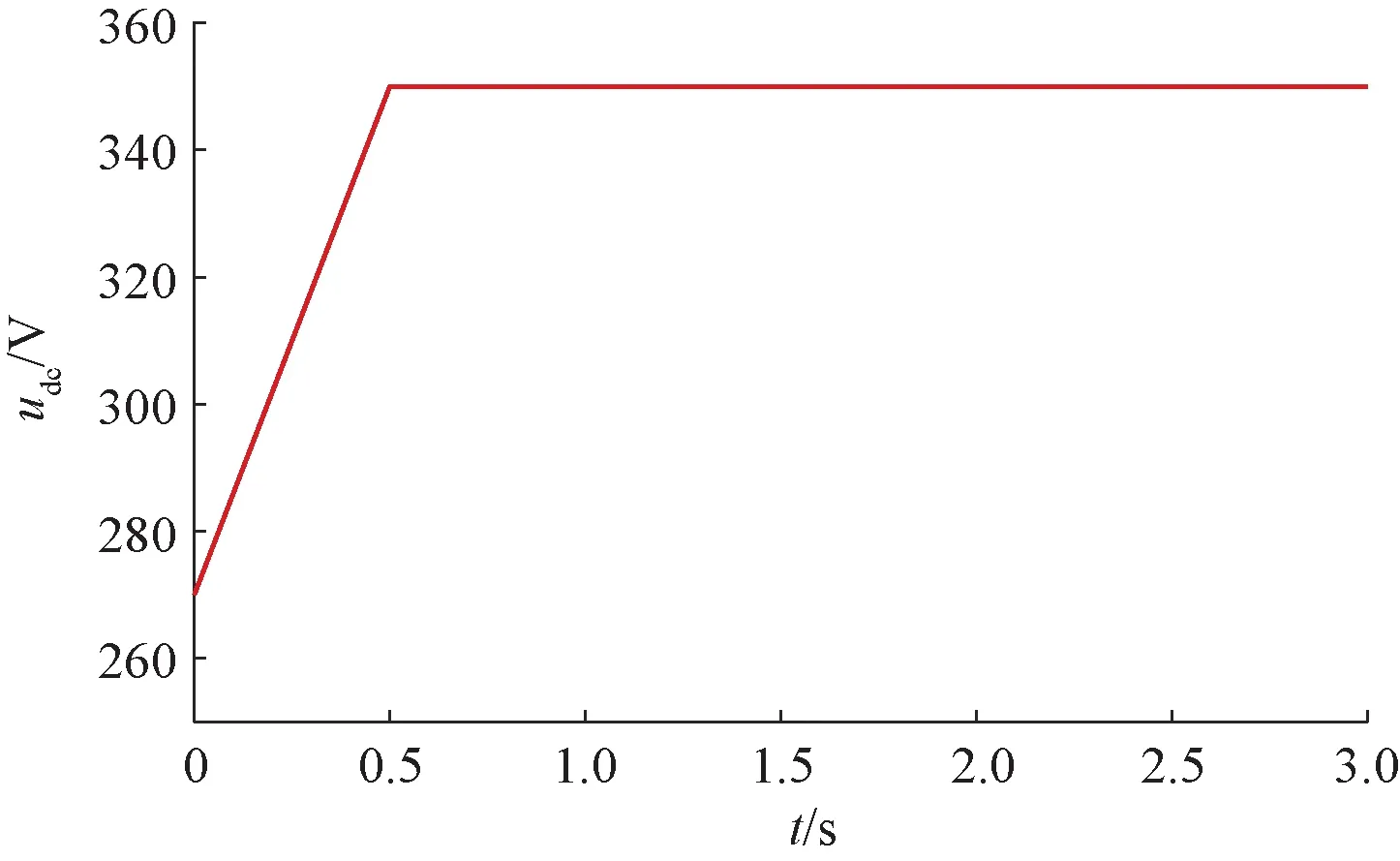
图8 母线电压设定

转速0～0.7 s上升到5 000 r/min，母线电压0～0.5 s从270 V上升到350 V模拟母线电压波动情况，得到输出三相电流iabc、id、iq、udc、转速如图9、图10所示。

图9 输出电流

图10 输出转矩转速检测

从图9可以看出，进入弱磁后id、iq持续降低，符合之前电压极限圆、电流极限圆推导，之后随着转速提高，进入深度弱磁区域，沿着MTPV曲线iq持续下降，id反向增加，符合MTPV曲线轨迹。在母线电压波动的情况下依旧可以进入深度弱磁并且转速达到了设定转速，达到预期实验目的。

7 结 语

本文从电机基本公式引入，简单介绍了目前常用的弱磁技术，介绍了表贴式和内置式电机基速以下id=0控制和MTPA控制的区别。并通过扫描法对永磁同步电机弱磁过程id、iq电流轨迹进行规划，通过规划MTPA、MTPV、等高线交点得到id、iq电流点，并通过MATLAB/Simulink进行m函数编译出表，并搭建模型仿真，通过仿真实验验证单张表转矩转速二维查表法，可以应对电压波动并且能够通过控制转矩转速进入深度弱磁区域，基本达到预期效果。