如何正确运用方差分析
——方差分析概述
2022-03-02胡纯严胡良平
胡纯严,胡良平,2*
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029
在运用统计学的过程中,离不开一些基本的统计量,例如平均指标(算术平均值、几何平均值、中位数等)和变异指标(方差、标准差、标准误等)等;也离不开一些基本的分析方法,例如差异性分析、相关分析、关联分析、回归分析、聚类分析和判别分析等。其中,“方差”和“方差分析(或称为F检验)”在统计学中具有重要的作用。本文将对方差分析的内容进行介绍。
1 与方差分析有关的基本概念
1.1 方差的定义
设X是一个随机变量,又设E(X)是随机变量X的数学期望(即算术平均值),若E(X2)存在,则称由式(1)定义的V(X)为X的总体方差(简称为方差)[1-2],通常记为V(X)或Va(rX)或σ2。
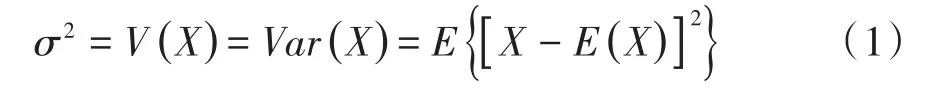
方差V(X)的单位是随机变量X的单位的平方,故在实际应用时,常取其算术平方根,令称其为标准差或均方差。显然,标准差σ与随机变量X具有相同的量纲。
设x1,…,xn是从特定总体中随机抽取的样本含量为n的一个样本,并设为该样本的样本均值,则样本方差由式(2)给出:

设总体中个体的数目为N,观测指标为X,其总体平均值为μ,总体方差也可由式(3)给出:
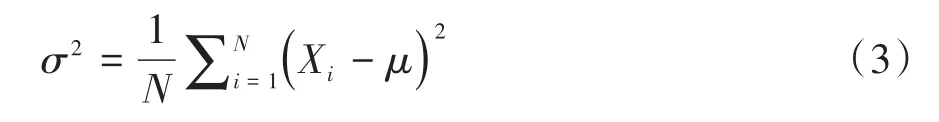
由数理统计知识可知:E(s2)=σ2,即样本方差是总体方差的无偏估计量。
1.2 方差的性质
随机变量X的方差V(X)具有如下性质:其一,设X=C(常数),则V(X)=0,即常数的方差为零。其二,设Y=CX(C为常数、X为随机变量),则V(Y)=C2V(X),即常数与随机变量之积的方差等于该常数的平方与该随机变量的方差之积。其三,设A、B是两个不相等的常数,则V(AX+B)=A2V(X)。其四,V(X)=E(X2)-[E(X)]2。其五,设X1与X2是两个相互独立的随机变量,则V(X1+X2)=V(X1)+V(X2),即两个相互独立的随机变量之和的方差等于它们各自方差之和[1-2]。这个性质可以推广到n个相互独立的随机变量,即设X1,…,Xn相互独立,则有下式成立:

1.3 方差的意义
一个随机变量的期望值(即均值)只能反映该随机变量平均取值的大小,而无法反映其取值的波动情况;方差是用来刻画一个随机变量的全部取值围绕其期望值波动程度大小的变异指标之一。虽然有类似功能的变异指标还包括标准差、变异系数和四分位数间距,但它们的应用场合远远少于方差。其根本原因在于方差中的主要部分是离均差平方和,人们可以依据资料中所包含的“变异来源的数目”对其进行分解,从而揭示因各变异来源所引起的数据波动的大小。尤其是在对调查资料进行统计分析时,当计算得出调查结果估计量之后,需要知道其估计的精度是多少,而精度最常用的度量是调查估计量的方差[3]。
1.4 方差分析的内容
1.4.1 方差的估计
对于来自复杂抽样设计的资料,研究者关注的是调查结果的方差大小,这就是方差估计问题[3]。由于调查结果的精度受抽样调查设计类型、样本含量、调查结果资料性质等因素的影响,故调查结果估计量的方差估计问题是一个非常复杂的统计学问题[3]。
1.4.2 方差的比较
方差的比较包括两方面内容:其一,比较地位平等的两个或多个方差之间的差别是否有统计学意义,以推断它们所代表的两个或多个总体的方差是否相等。与此研究目的对应的假设检验被称为方差齐性检验[4-5]。其二,比较地位可能不平等的两个或多个方差(例如某因素各水平组间方差与组内方差、某因素各水平组间方差与包含该因素的统计模型的误差的方差)之间的差别是否有统计学意义,以推断不同变异来源对试验结果平均效应的影响是否有统计学意义。第二方面的内容就是基于均值比较的方差分析,通常被称为一元或多元单因素方差分析或多因素方差分析[6-7]。
在前述提及的第二方面内容中,若观测结果变量为定量变量且构建的回归模型是多重线性回归模型,基于两个嵌套回归模型(其中一个为包含所有自变量的全模型、另一个为仅包含部分自变量的部分模型)的残差方差的比较,可推断出是否可用部分模型取代全模型[6]。
2 方差分析的数学基础——F分布
2.1 F分布的历史
F分布是一种连续型分布,它不仅是方差分析的基础,还与正态分布、χ2分布和t分布都有密切联系。最初,人们是通过研究组间方差与组内方差之比入手的。Fisher于1924年发现方差比有一个分布,并以的形式来编表。
2.2 F分布的定义

在式(5)中,F的分布称为分子和分母的自由度分别为m和n的F分布[8],并记作F~Fm,n。F分布的密度函数见式(6):

2.3 F分布的性质
2.3.1 概率密度函数的图形
在f(x;m,n)中,m为分子的自由度,n为分母的自由度,当m=10,n分别取4、10、50、∞时,F分布的概率密度函数图形见图1;当n=10,m分别取4、10、50、∞时,F分布的概率密度函数图形见图2。

图1 第一组条件下F分布概率密度函数图形

图2 第二组条件下F分布概率密度函数图形
F分布概率密度函数图形特点如下:①f(x;m,n)的形状受分子和分母自由度的影响,固定其中一个自由度,改变另一个自由度,可以得到两簇密度函数曲线;②单侧F分布表用于方差分析,双侧F分布表用于两总体方差齐性检验。
通常是已知右侧尾端概率p(单侧)或双侧尾端概率p(双侧)、分子和分母的自由度m和n,去查F分布的分位数(也称为临界值)。单、双侧时,分别由式(8)和式(9)来确定横轴上的分位数F。
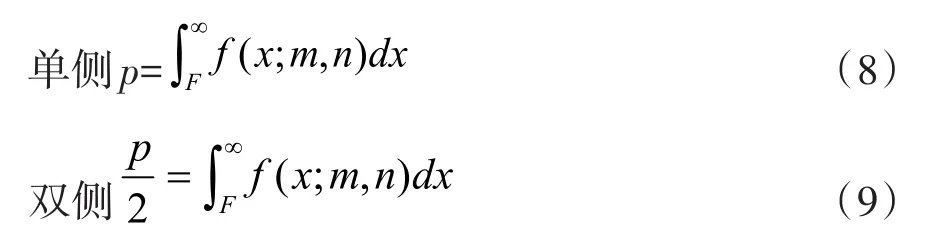
双侧时,左侧分位数F可由下式算出:,它通常小于1,而在计算两样本方差比时,特意将较大方差放在分子上,故用于检验两总体方差齐性的F统计量的值通常大于等于1。因此,制表时,即使是双侧分位数,也只列出右侧的分位数,省略了左侧的分位数。
2.3.2 倒数变换后的随机变量仍服从F分布
服从F分布的随机变量的倒数仍是服从F分布的随机变量,但需要调换分子与分母的自由度,即若X~Fm,n,Y=1/X,则有下式:

2.3.3 F分布与其他分布之联系
若 X~tn,则 X2~F1,n;若,则 X~mFm,∞;若 X~z(标准正态变量),则X2~F1,∞。总结上述关系,可得到式(11):

在应用中,利用上述关系有时可将一种检验转化为另一种检验,或用来核对计算是否正确。
2.3.4 服从F分布的随机变量经对数变换后服从正态分布
若 X~Fm,n,令Zm,n=lnX,则当m和n都较大时,Zm,n的分布近似于式(12):

3 方差分析在差异性检验中的应用
3.1 用于均值比较的方差分析
在分析试验资料时,若观测结果为定量资料,一个最常见的分析目的就是比较某试验因素在不同水平条件下定量观测指标平均值之间的差别是否有统计学意义。在单因素试验研究场合下,需要进一步考察试验设计的具体类型和定量资料所满足的前提条件,方可选择合适的差异性检验方法。通常,单因素试验设计类型可分为以下四种:单组设计、配对设计、成组设计和单因素多水平设计;定量资料可分为满足和不满足参数检验前提条件(即独立性、正态性和方差齐性)这两种情形。
当定量资料满足参数检验的前提条件且设计类型为“单组设计、配对设计和成组设计”三种时,人们习惯于选择基于t分布为理论依据的t检验;而当定量资料满足参数检验的前提条件且设计类型为“单因素多水平设计”时,统计学上要求进行方差分析。
在多因素试验研究场合下,当定量资料满足参数检验的前提条件且设计类型为“某种特定的多因素设计”时,统计学上强调必须选用与特定设计类型对应的方差分析方法处理定量资料。常见的多因素试验设计类型包括随机区组设计、拉丁方设计、交叉设计、析因设计、嵌套(或系统分组)设计、具有重复测量因素的设计和正交设计等。
3.2 用于方差比较的方差分析
实施用于均值比较的方差分析的一个重要前提条件是方差齐性,即某试验因素各水平组总体方差相等。SAS/STAT的GLM过程中介绍了4种方差齐性检验方法:Bartlett’sχ2检验、Levene’sF检验、O′Brien’sF检验以及Brown和Forsythe提出的F检验方法。另外,基于两样本方差之比构造出检验统计量来推断两总体方差是否相等的检验方法,也属于用于方差比较的方差分析。
3.3 用于线性回归模型评价的方差分析
假定在一个包含k(k≥2)个自变量和一个定量因变量且样本含量为n的统计资料中,先构建一个包含全部k(k≥2)个自变量(假定每个自变量都以一次方形式出现,未引入任何派生自变量)的多重线性回归模型,得到其残差的离差平方和记为SSFR,自由度记为dfFR;依据专业知识,从k(k≥2)个自变量中取出m(m 在式(13)中,F服从分子与分母自由度分别为df1和dfFR的F分布;∆=SSPR-SSFR,df1=dfPR-dfFR。若检验统计量F值大于临界值则表明不能采用简化回归模型取代全模型,反之亦然。 方差分析的基本思想是对定量结果变量Y的总离均差平方和的分解。分解出来的项数为所考查的影响因素(包含拟考查的因素之间的交互作用项)的项数加一个误差项。由于基于均值比较的方差分析与试验设计类型和拟考查的交互作用项数有密切关系,故对定量结果变量Y的总离均差平方和的分解结果将会随具体情况而变化。下面给出两种常见试验设计类型对应的总离均差平方和分解的样例。 设试验因素A有k个水平,各水平下独立重复试验次数为nj(j=1,2,…,k);又设在第j个水平下第i(j=1,2,…,nj)次独立重复试验结果为Yij,设该水平条件下Y的平均值为;再设定量结果变量Y的总均值为Yˉ..。则定量结果变量Y的总离均差平方和的分解结果见式(14): 在式(14)中,SSA和SSE分别代表因素A和误差E的离均差平方和,表达式见式(15)、式(16): 设试验因素A有k个水平,区组因素B有c个水平,试验因素A各水平下都独立重复试验c次;又设在第j个水平下第i(i=1,2,…,c)次独立重复试验结果为Yij;再设定量结果变量Y的总均值为则定量结果变量Y的总离均差平方和的分解结果见式(17): 在式(17)中,SSA、SSB和SSE分别代表因素A、因素B和误差E的离均差平方和,具体表达式见式(18)、式(19)、式(20): 在总离均差平方和被正确分解之后,进行方差分析就需要构造出检验统计量F,然后基于样本数据计算出检验统计量F的值,再依据F分布做出接受或拒绝无效假设的结论。也就是说,检验统计量F是与特定无效假设和备择假设相对应的。 4.4.1 与单因素多水平设计一元定量资料对应的方差分析 第一步,建立检验假设。H0:因素A各水平下定量观测结果Y的平均值相等;H1:因素A各水平下定量观测结果Y的平均值不等或不全相等;给定显著性水平α的值,通常取α=0.05。 第二步,构造检验统计量F,见式(21),其中n为总样本含量,F服从分子与分母自由度分别为(k-1)与(n-k)的F分布。 第三步,做出统计结论。计算出检验统计量F的值,若F大于等于F分布下右侧尾端概率为α=0.05对应的临界值,可得出拒绝无效假设H0、接受备择假设H1的统计结论。 4.4.2 与随机区组设计一元定量资料对应的方差分析 与“第4.4.1节”步骤基本相同,不同的是需要构造两个检验统计量,分别用于检验因素A和因素B。因篇幅所限,现将两个检验统计量扼要呈现如下,见式(22)、式(23): 总离均差平方和的分解方法不是唯一的,它与分解方法所依据的统计假设密切相关。在SAS/STAT的GLM过程[5]中,基于一般线性模型的理论进行方差分析时,对总离均差平方和给出了四种分解方法,分别为I型、II型、III型和IV型离均差平方和。在对多因素轻度非平衡(不同试验因素水平组合条件下独立重复试验次数不等,但没有一种组合条件下重复试验次数为0)试验设计定量资料进行方差分析时,基于四型离均差平方和所得到的方差分析结果不尽相同(此时,III型和IV型离均差平方和所对应的方差分析结果相同);尤其是在严重非平衡(不同试验因素水平组合条件下独立重复试验次数不等,且部分组合条件下重复试验次数为0)试验设计条件下,基于四型离均差平方和所得到的方差分析结果几乎完全不同。 虽然方差分析可用于分析多因素试验研究资料,但它一般是由多次F检验组成的。因为每次F检验都只针对一个因素或交互作用项;而当某因素的水平数大于2,且当F检验的结果为该因素的全部水平条件下定量结果变量的均值之间差异有统计学意义时,还需要进行多重比较。一般来说,不适合采用简单的t检验[9-10]进行多重比较,而需要根据不同的要求和精度,从众多的多重比较方法中选用最符合分析要求的方法[5]。 本文介绍了与方差分析有关的内容,包括基本概念、方差分析的数学基础——F分布、方差分析在差异性检验中的应用场合以及基于均值比较的方差分析的基本思想。最后,在讨论部分中提出了“四型离均差平方和”的概念。之所以介绍这些在常规统计学教科书中几乎未曾提及过的内容,以引起读者的兴趣和思考。
4 基于均值比较的方差分析的基本思想
4.1 概述
4.2 单因素多水平设计一元定量资料总离均差平方和的分解


4.3 随机区组设计一元定量资料总离均差平方和的分解


4.4 检验统计量F的构造

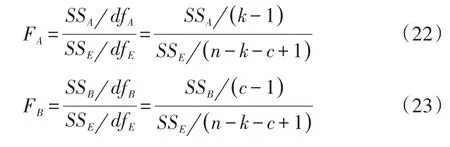
5 讨论与小结
5.1 讨论
5.2 小结
